11 6 Solving 11 6 Solving Trigonometric Equations

11 -6 Solving 11 -6 Solving. Trigonometric. Equations Warm Up Lesson Presentation Lesson Quiz Holt. Mc. Dougal Algebra 2 Holt

11 -6 Solving Trigonometric Equations Warm Up Solve. 1. x 2 + 3 x – 4 = 0 x = 1 or – 4 2. 3 x 2 + 7 x = 6 Evaluate each inverse trigonometric function. 3. Tan-1 1 45° 4. Sin-1 – 60 Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Objective Solve equations involving trigonometric functions. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Unlike trigonometric identities, most trigonometric equations are true only for certain values of the variable, called solutions. To solve trigonometric equations, apply the same methods used for solving algebraic equations. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 1: Solving Trigonometric Equations with Infinitely Many Solutions Find all the solutions of sinθ = sinθ + Method 1 Use algebra. Solve for θ over the principal value of sine, – 90° ≤ θ ≤ 90°. sinθ = sinθ + sinθ = Subtract sinθ = Combine like terms. Holt Mc. Dougal Algebra 2 sinθ from both sides.

11 -6 Solving Trigonometric Equations Example 1 Continued sinθ = Multiply by 2. θ = sin-1 Apply the inverse sineθ. θ = 30° Find θ when sinθ = Find all real number value of θ, where n is an integer. θ = 30° + 360°n Use the period of the sine function. Use reference angles to find θ = 150° + 360°n other values of θ. Holt Mc. Dougal Algebra 2

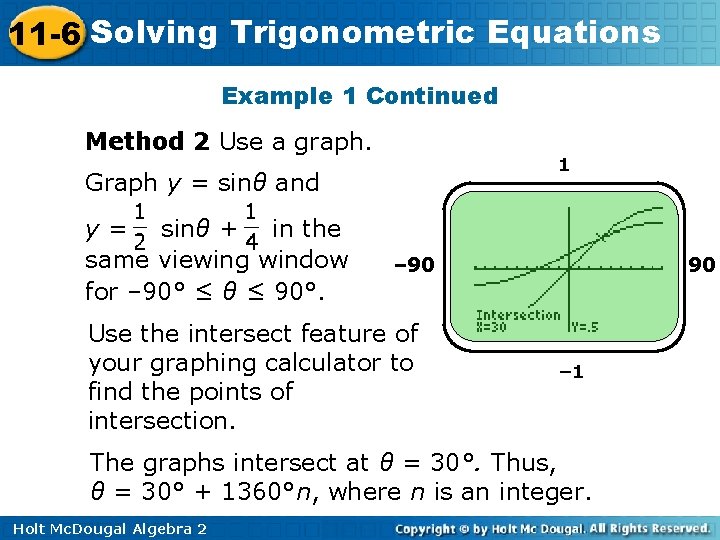
11 -6 Solving Trigonometric Equations Example 1 Continued Method 2 Use a graph. 1 Graph y = sinθ and y = sinθ + in the same viewing window for – 90° ≤ θ ≤ 90°. – 90 Use the intersect feature of your graphing calculator to find the points of intersection. 90 – 1 The graphs intersect at θ = 30°. Thus, θ = 30° + 1360°n, where n is an integer. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Check It Out! Example 1 Find all of the solutions of 2 cosθ + = 0. Method 1 Use algebra. Solve for θ over the principal value of sine, 0 ≤ θ ≤ . 2 cosθ = Subtract from both sides. Divide both sides by 2. θ = cos-1 – Apply the inverse cosineθ. θ = 150° Find θ when cosine θ = Holt Mc. Dougal Algebra 2 .

11 -6 Solving Trigonometric Equations Check It Out! Example 1 Continued θ = 150° + 360°n, 210° +360°n. Use reference angles to find other values of θ. Method 2 Use a graph. 2 Graph y = 2 cosθ and y= in the same – 360 viewing window for – 360° ≤ θ ≤ 360°. – 2 The graphs intersect at θ = 150°. Thus, θ = 150° + 360°n, where n is an integer. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Some trigonometric equations can be solved by applying the same methods used for quadratic equations. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 2 A: Solving Trigonometric Equations in Quadratic Form Solve each equation for the given domain. 4 tan 2θ – 7 tanθ + 3 = 0 for 0° ≤ θ ≤ 360°. 4 tan 2θ – 7 tanθ + 3 = 0 (tanθ – 1)(4 tanθ – 3) = 0 Holt Mc. Dougal Algebra 2 Factor the quadratic expression by comparing it with 4 x 2 – 7 x + 3 = 0. Apply the Zero Product Property.

11 -6 Solving Trigonometric Equations Example 2 A Continued tanθ = 1 or tan θ = tan-1(1) = 45° or 225° Holt Mc. Dougal Algebra 2 θ = tan-1 Apply the inverse tangent. Use a calculator. Find all angles ≈ 36. 9° or 216. 9° for 0°≤ θ ≤ 360°.

11 -6 Solving Trigonometric Equations Example 2 B: Solving Trigonometric Equations in Quadratic Form 2 cos 2θ – cosθ = 1 for 0 ≤ θ ≤ . 2 cos 2θ – cosθ – 1 = 0 (2 cosθ + 1) (cosθ – 1) = 0 cosθ = θ= Holt Mc. Dougal Algebra 2 or cosθ = 1 or θ = 0 Subtract 1 from both sides. Factor the quadratic expression by comparing it with 2 x 2 – x + 1 = 0. Apply the Zero Product Property. Find both angles for 0 ≤ θ ≤ .

11 -6 Solving Trigonometric Equations Check It Out! Example 2 a Solve each equation for 0 ≤ θ ≤ 2. cos 2 θ + 2 cosθ = 3 cos 2 θ + 2 cosθ – 3 = 0 (cosθ – 1)(cosθ + 3) = 0 cosθ = 1 or cosθ = – 3 Subtract 3 from both sides. Factor the quadratic expression by comparing it to x 2 +2 x – 3 = 0. Apply the Zero Product Property. cosθ = – 3 has no solution because – 3 ≤ cosθ ≤ 1. cosθ = 2 or 0 Holt Mc. Dougal Algebra 2 The only solution will come from cosθ = 1.

11 -6 Solving Trigonometric Equations Check It Out! Example 2 b Solve each equation for 0 ≤ θ ≤ 2. sin 2θ + 5 sinθ – 2 = 0 The equation is in quadratic form but can not be easily factored. Use the quadratic formula. sinθ = Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Check It Out! Example 2 b Continued Apply the inverse sine. Use a calculator. Find both angles. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations You can often write trigonometric equations involving more than one function as equations of only one function by using trigonometric identities. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 3 A: Solving Trigonometric Equations with Trigonometric Identities Use trigonometric identities to solve each equation. tan 2θ + sec 2θ = 3 for 0 ≤ θ ≤ 2π. 2 2 tan 2θ + (1 + tan 2θ) – 3 = 0 Substitute 1 + tan θ for sec θ by the Pythagorean identity. 2 tan 2θ – 2 = 0 Simplify. Divide by 2. tan 2θ – 1 = 0 (tanθ – 1)(tanθ + 1) = 0 Factor. tanθ = 1 or tanθ = – 1 Apply the Zero Product Property. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 3 A Continued Check Use the intersect feature of your graphing calculator. A graph supports your answer. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 3 B: Solving Trigonometric Equations with Trigonometric Identities Use trigonometric identities to solve each equation. cos 2θ = 1 + sin 2θ for 0° ≤ θ ≤ 360° (1 – sin 2θ) – 1– sin 2θ = 0 Substitute 1 – sin 2θ for cos 2θ by the Pythagorean identity. – 2 sin 2θ = 0 Simplify. sin 2θ = 0 Divide both sides by – 2. sinθ = 0 Take the square root of both sides. θ = 0° or 180° or 360° Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 3 B Continued cos 2θ = 1+sin 2θ for 0° ≤ θ ≤ 360° θ = 0° or 180° or 360° Check Use the intersect feature of your graphing calculator. A graph supports your answer. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Check It Out! Example 3 a Use trigonometric identities to solve each equation for the given domain. 4 sin 2θ + 4 cosθ = 5 2θ for sin 2θ Substitute 1 – cos 4(1 - cos 2θ) + 4 cosθ – 5 = 0 by the Pythagorean identity. 4 cos 2θ – 4 cosθ + 1 = 0 Simplify. (2 cos 2θ – 1)2 = 0 Factor. Take the square root of both sides and simplify. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Check It Out! Example 3 b Use trigonometric identities to solve each equation for the given domain. sin 2θ = – cosθ for 0 ≤ θ < 2 2 cosθsinθ + cosθ = 0 cosθ(2 sinθ + 1) = 0 Substitute 2 cosθsinθ for sin 2θ by the double-angle identity. Factor. Apply the Zero Product Property. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Example 4: Problem-Solving Application On what days does the sun rise at 4 A. M. on Cadillac Mountain? The time of the sunrise can be modeled by Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 1 Understand the Problem The answer will be specific dates in the year. List the important information: • The function model is t(m) = 1. 665 (m + 3) + 5. 485. • Sunrise is at 4 A. M. , which is represented by t = 4. • m represents the number of months after January 1. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 2 Make a Plan Substitute 4 for t in the model. Then solve the equation for m by using algebra. 3 Solve 4 = 1. 665 sin (m + 3) + 5. 485 Substitute 4 for t. Isolate the sine term. sin-1(– 0. 8918) = Holt Mc. Dougal Algebra 2 (m + 3) Apply the inverse sine θ.

11 -6 Solving Trigonometric Equations Sine is negative in Quadrants lll and l. V. Compute both values. Qlll: π + sin-1(0. 8918) Holt Mc. Dougal Algebra 2 Ql. V: 2π + sin-1(0. 8918)

11 -6 Solving Trigonometric Equations Using an average of 30 days per month, the date m = 5. 10 corresponds to June 4(5 months and 3 days after January 1) and m = 6. 90 corresponds to July 28 (6 months and 27 days after January 1). Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 4 Look Back Check your answer by using a graphing calculator. Enter y = 1. 665 sin (x + 3) + 5. 485 and y = 4. Graph the functions on the same viewing window, and find the points of intersection. The graphs intersect at early June and late July. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Check It Out! Example 4 The number of hours h of sunlight in a day at Cadillac Mountain can be modeled by h(d) = 3. 31 sin (d – 85. 25) + 12. 22, where d is the number of days after January 1. When are there 12 hours of sunlight. 1 Understand the Problem The answer will be specific dates in the year. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 1 Understand the Problem The answer will be specific dates in the year. List the important information: • The function model is h(d) = 3. 31 sin (d – 85. 25) + 12. 22. • The number of hours of sunlight in the day, which is represented by h = 12. • d represents the number of days after January 1. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 2 Make a Plan Substitute 12 for h in the model. Then solve the equation for d by using algebra. 3 Solve 12 = 3. 31 sin (d – 85. 25) + 12. 22 Substitute 12 for h. Isolate the sine term. Apply the inverse sine θ. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Sine is negative in Quadrants lll and l. V. Compute both values. Qlll: 81. 4 ≈ d Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Ql. V: 271. 6 ≈ d Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations 4 Look Back Check your answer by using a graphing calculator. Enter y = 3. 31 sin (d – 85. 25) + 12. 22 Graph the functions on the same viewing window, and find the points of intersection. The graphs intersect in late March and late September. Holt Mc. Dougal Algebra 2

11 -6 Solving Trigonometric Equations Lesson Quiz 1. Find all solutions for cosθ = – cosθ. θ = 45° + n 360° or 315° + n 360° 2. Solve 3 sin 2θ – 4 = 0 for 0 ≤ θ ≤ 360°. θ ≈ 221. 8° or 318. 2° 3. Solve cos 2θ = 3 sinθ + 2 for 0 ≤ 2π. Holt Mc. Dougal Algebra 2