Lecture 3 Indefinite and Definite Integrals the Fundamental







































- Slides: 45

Lecture 3: Indefinite and Definite Integrals, the Fundamental Theorem of Calculus, Integration Via Substitution, Integration by Parts, Computing Areas, Computing Volumes by the Disk and Shell Methods

Part I: Indefinite and Definite Integrals and the Fundamental Theorem of Calculus

Objectives • Know the meaning of indefinite integrals and know how they are related by the first Fundamental Theorem of Calculus • Know how to evaluate simple definite integrals by taking the limit as we split the area into more and more blocks (without the first Fundamental Theorem of Calculus)

What is an integral? •

• Example Indefinite Integrals

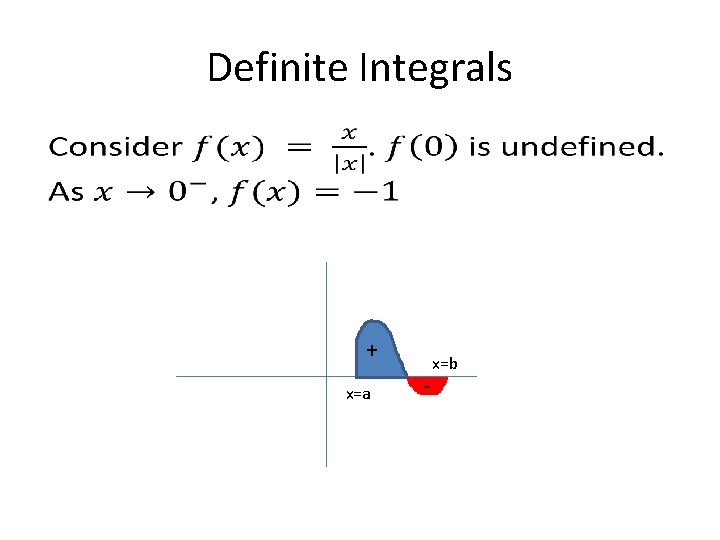
Definite Integrals • x=a x=b

Definite Integrals • + x=a - x=b

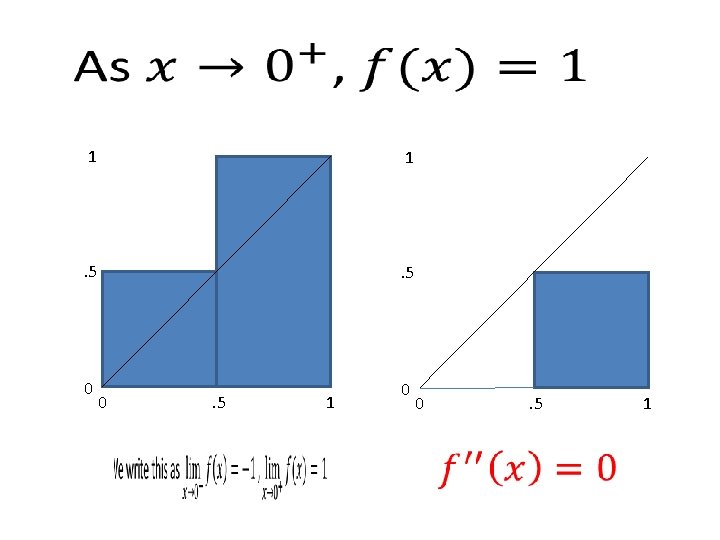
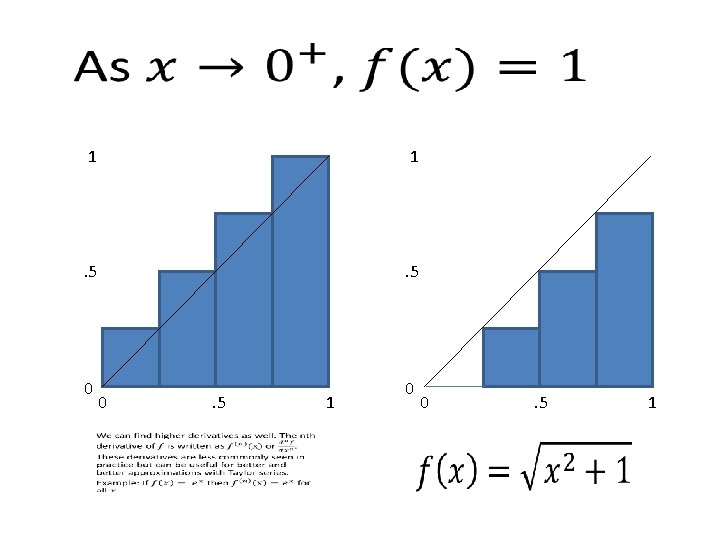
Computing Definite Integrals • How do we compute these areas? • Idea (Riemann): Obtain better and better upper and lower bounds by breaking the area up into smaller and smaller pieces. If these bounds match in the limit as the width of these pieces goes to 0, this is the area.

1 1 . 5 0 0 0 . 5 1

1 1 . 5 0 0 0 . 5 1

What if we break it into n pieces?

Fundamental Theorem of Calculus •

Fundamental Theorem of Calculus • t=x+Δx t=a t=x

Fundamental Theorem of Calculus •

Part II: Differentials and the Substitution Rule

Objectives • Be able to compute and use differentials • Be fluent in integrating by substitution Corresponding Sections in Simmons: 5. 2, 5. 3

Differentials •

Differentials and Differentiation Rules •

Differentials continued • What exactly does all this mean? • One approach: dx and df are small changes in x and y for the tangent line to f at x rather than f itself. • This is exact, but somewhat strange • Excellent but non-rigorous approach: Think of df and dx as “infinitesimal” changes in f and x so the higher order terms don’t matter. • Either way, differentials work perfectly in practice

Integration by Substitution •

Examples •
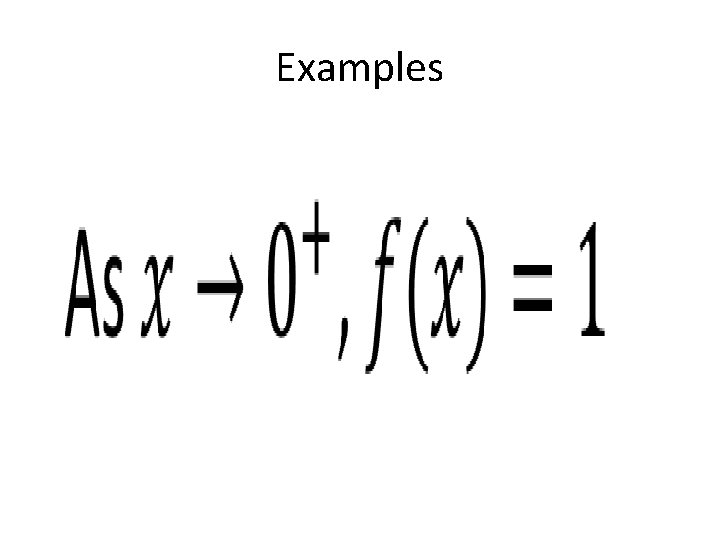
Examples •

Integration by Substitution •
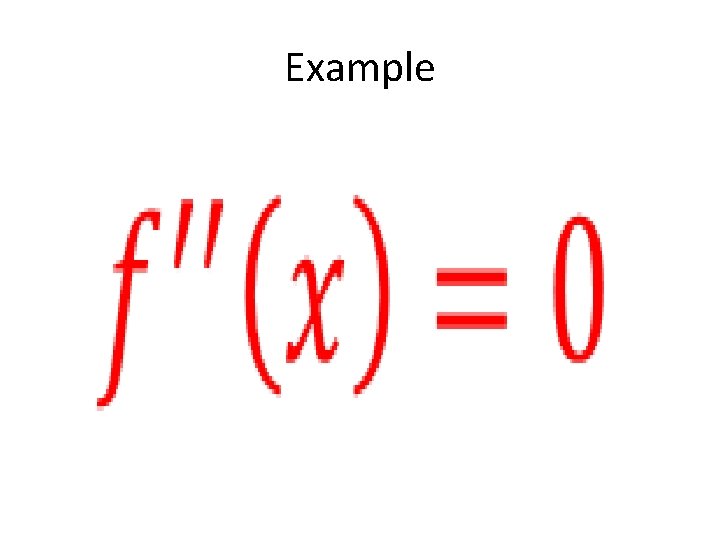
Example •

Part III: Integration by Parts

Objectives • Be able to integrate by parts • Corresponding section in Simmons: 10. 7

Integration by parts •

Integration by parts formula •

Example •

Example continued •

Guidelines for choosing u and v •

Guidelines for choosing u and v •

Special example •

Part IV: Computing Areas and Volumes

Objectives • Know how to find areas and how to find volumes by the disk and shell methods Corresponding sections in Simmons: 7. 3, 7. 4

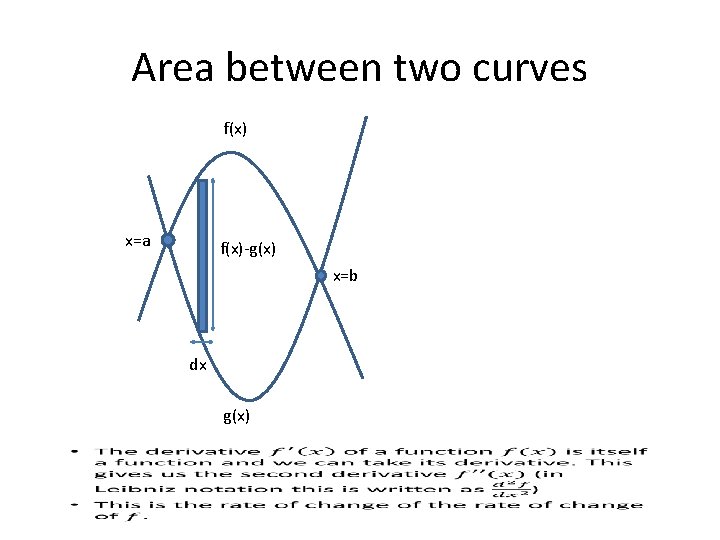
Area between two curves f(x) x=a f(x)-g(x) x=b dx g(x)

Example •

Example •

Volumes by disks x=a x=b

Example: Cone •

Example: Sphere •

The Washer Method •

The Shell Method •

Example: Cone •

Example: Sphere •
 Integral vs definite integral
Integral vs definite integral Substitution rule for definite integrals
Substitution rule for definite integrals Riemann sum to integral notation
Riemann sum to integral notation Additive interval property
Additive interval property Definite integral denotes
Definite integral denotes Exploration 1-3a introduction to definite integrals
Exploration 1-3a introduction to definite integrals Circuit training properties of definite integrals
Circuit training properties of definite integrals Properties of indefinite integrals
Properties of indefinite integrals Definite vs definitive
Definite vs definitive Amigo definite article
Amigo definite article Spanish definite articles
Spanish definite articles Indefinite article for mochila
Indefinite article for mochila Les articles indéfinis examples
Les articles indéfinis examples Definite vs indefinite articles spanish
Definite vs indefinite articles spanish Italian definite article
Italian definite article Adverb frequency examples
Adverb frequency examples Chica definite article
Chica definite article Indefinite vs definite articles spanish
Indefinite vs definite articles spanish Agenda web definite and indefinite article
Agenda web definite and indefinite article Profesoras definite article
Profesoras definite article German definite and indefinite articles
German definite and indefinite articles Is the shape of a liquid definite or indefinite
Is the shape of a liquid definite or indefinite Definite article french
Definite article french Indefinite adjectives and pronouns
Indefinite adjectives and pronouns 01:640:244 lecture notes - lecture 15: plat, idah, farad
01:640:244 lecture notes - lecture 15: plat, idah, farad Radiation integrals and auxiliary potential functions
Radiation integrals and auxiliary potential functions Fourier series and integrals
Fourier series and integrals Integrals involving powers of secant and tangent
Integrals involving powers of secant and tangent The fundamental theorem of calculus
The fundamental theorem of calculus Given symbol
Given symbol Sec 7
Sec 7 Integral
Integral Integral trig identities
Integral trig identities U substitution
U substitution Surface integral of scalar function
Surface integral of scalar function Line integral of triangle
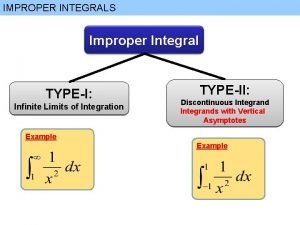
Line integral of triangle Improper integrals
Improper integrals Average rate of change integrals
Average rate of change integrals Maurits w. haverkort
Maurits w. haverkort Application of residue theorem to evaluate real integrals
Application of residue theorem to evaluate real integrals Calculus chapter 5 integrals
Calculus chapter 5 integrals Chain rule integration
Chain rule integration Simple pole
Simple pole Kompetensi dasar integral
Kompetensi dasar integral Product rule of integration
Product rule of integration Double integrals in polar coordinates
Double integrals in polar coordinates