INTEGRAL GARIS Di dalam integral Garis kita akan



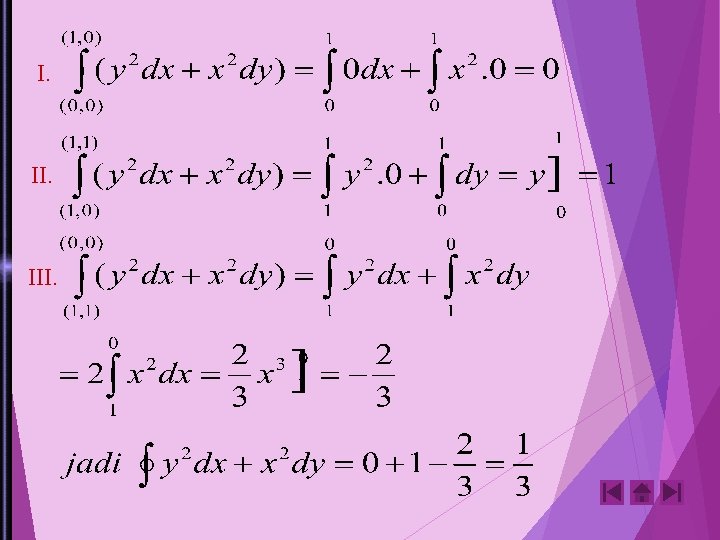



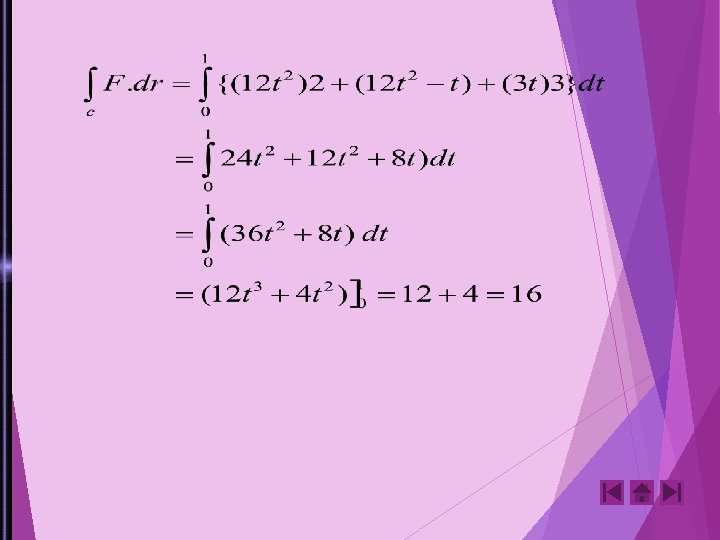
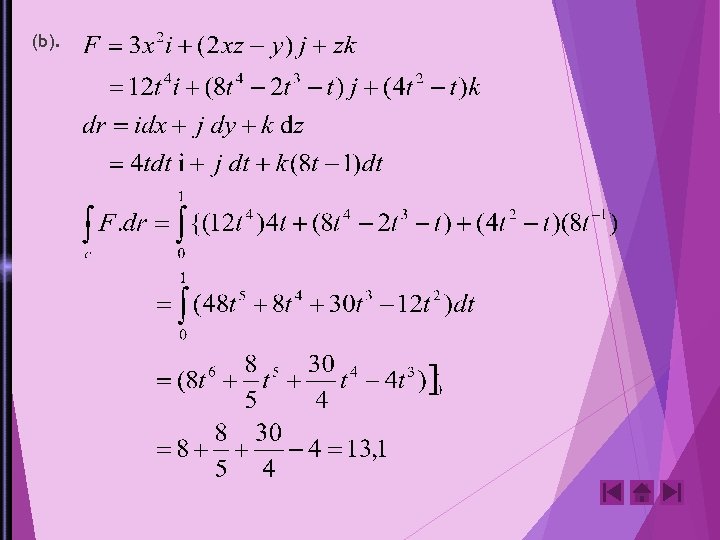
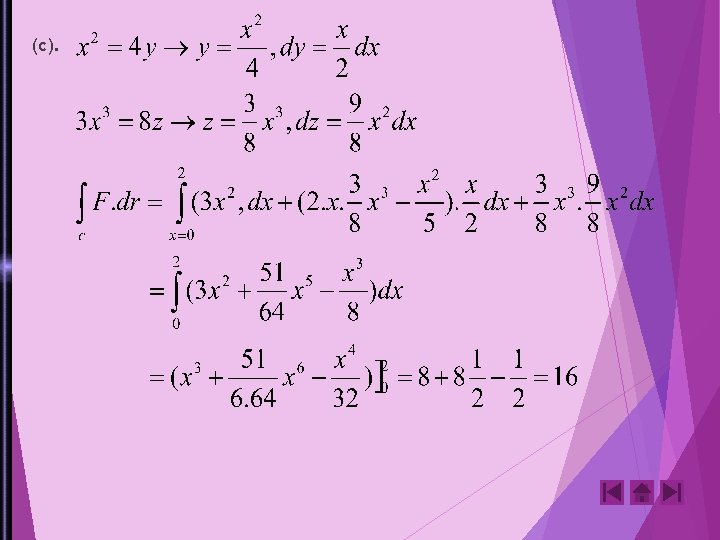








- Slides: 18

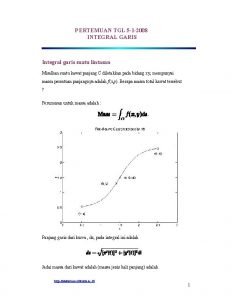
INTEGRAL GARIS Di dalam integral Garis kita akan mengintegralkan sepanjang kurva C di dalam ruang (Bidang) dan yang di Integralkan akan merupakan fungsi yang terdefinisi pada setiap sisi dari C. Integral Garis yang lazim adalah panjang Busur, yang dinyatakan dengan : Jika C adalah kurva tertutup (kurva yang memotong dirinya sendiri), maka integral mengelilingi C yang sering ditunjukkan oleh:

Contoh : 1. Hitunglah (xy 2 dx + x 2 y dy), dengan C adalah Busur Parabola y = x 2 dari ( -1, 1) sampai (0, 0) Jawab: (xy 2 dx + x 2 y dy) : = = =

2. Hitunglah , dengan C adalah segitiga dengan ujung-ujung (1, 0), (1, 1) dan (0, 0) Jawab: sebagai parameter dapat digunakan variabel X, integral C terdiri atas 3 potong garis sehingga. Membentuk 3 integral, yaitu = y y=x III (0, 0) (1, 1) y=x dy=dx II I (1, 0) x
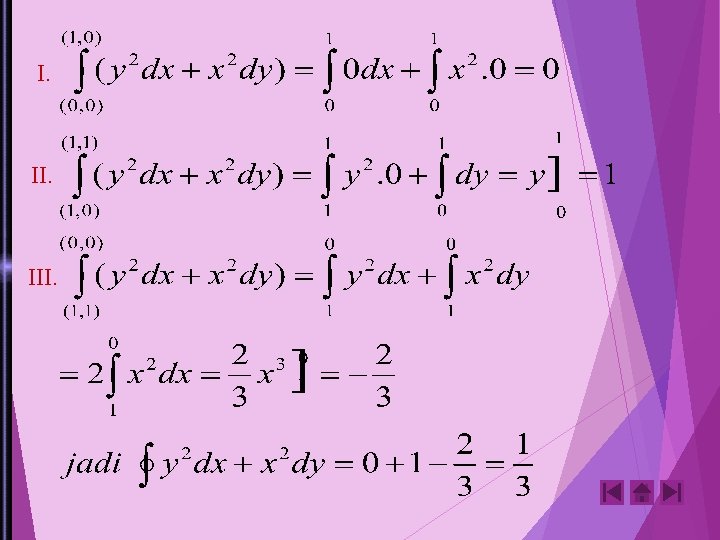
I. III.

Integral Garis Sebagai Integral Vektor Mis. r(t)i + y(t)j + z(t)k, dimana r(t) adalah vektor posisi dari (x, y, z) mendefinisikan sebuah kurva yang menghubungkan titik-titik P 1 dan P 2. Mis. A(x, y, z) = A 1 i + A 2 j + A 3 k sebuah fungsi vektor dari posisi yang didefinisikan dan kontinu sepanjang C, maka integeral garis sepanjang C dan P 1 ke P 2, ditulis sebagai : Jika A adalah gaya F pada sebuah partikel yang bergerak sepanjang C, maka integeral garis ini menyatakan usaha yang dilakukan oleh gaya. Jika C adalah kurva tertutup, maka integeral yang mengelilingi C ditunjukan oleh :

Contoh: 1. Carilah usaha total yang dilakukan untuk menggerakan sebuah partikel dalam medan gaya yang diberikan oleh F = 3 xyi – 5 zj + 10 xk sepanjang kurva x = t 2 + 1, y = t 2, z = t 3 dari t = I hingga t = 2 Jawab : Usaha total = = 3 xy dx – 5 z dy + 10 x dz

2. Carilah usaha yang dilakukan dalam menggerakkan sebuah partikel dalam medan gaya F=3 x 2 i+(2 xz-y)j+zk sepanjang (a). Garis lurus (0, 0, 0) ke (2, 1, 3) (b). Kurva ruang x=2 t 2 , y=t , z=4 t 2 -t dari t=0 ke t=1 (c). Kurva yang didefinisikan oleh: x 2 = 4 y, 3 x 3 =8 z dari x=0 ke x=2 Jawab: (a). garis lurus yang menghubungkan (0, 0, 0) dan (2, 1, 3) dalam bentuk parameter diberikan oleh: x=2 t, y=t dan z=3 t F=3 x 2 i + (2 xz-y 2 j+zk =12 t 2 i+ (12 t 2 – t)j+3 z k dr=dx i+dy. j + d z k =(2 i + j + 3 k) dt
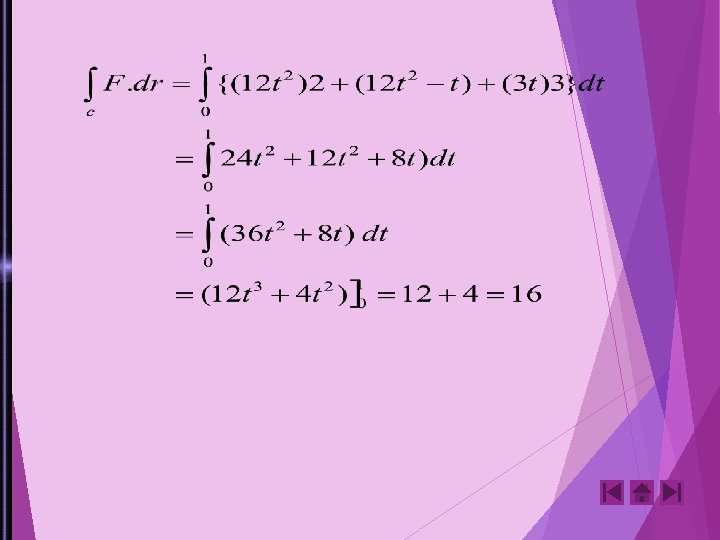
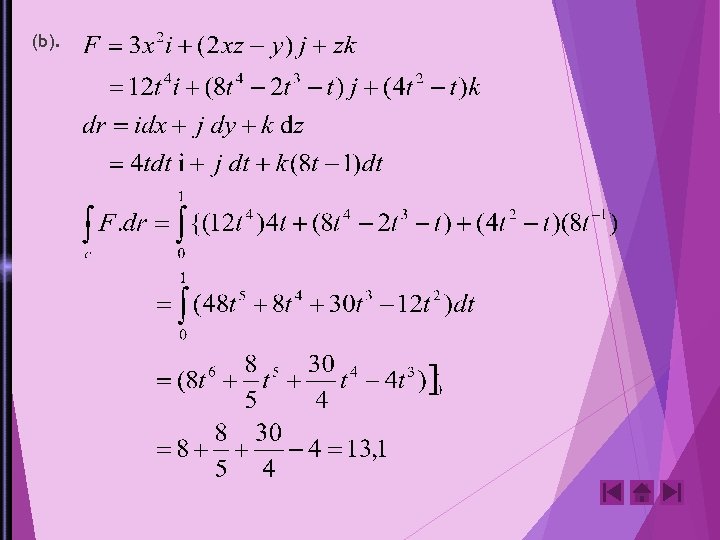
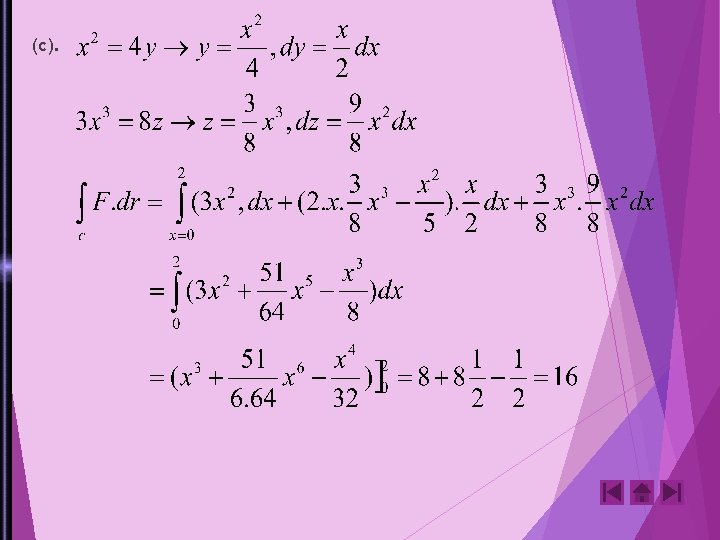

Ketidaktergantungan Integeral Garis Pada Lintasan Jika fungsi P(x, y, z) dan Q(x, y, z) dan R(x, y, z) didefinisikan dan kontinu dalam Domain D. Integeral garis P dx + Q dy + R dz dikatakan tidak tergantung pada lintasan di D, jika untuk setiap pasang titik – titik ujung A dan B di D, nilai integeral garisnya adalah : sama untuk semua lintasan C dari A dan B. Nilai integeral hanya tergantung pada pemilihan A dan B, tetapi tidak pada jenis lintasan yang menghubungkan titik A dan B, seperti yang ditunjukan pada gambar dibawah ini: B C 1 D C 2 A C 3 Nilai integeral pada lintasan c 1, c 2 dan c 3 adalah sama.

Teorema Jika A=ΔΦ Pada semua titik dalam suatu daerah J dari ruang, yang didefinisikan oleh : a 1 , ≤, x ≤ a 2 b 1 ≤ y ≤ b 2 , c 1 ≤ z ≤ c 2 , dimana Φ (x, y, z) berharga tunggal dan memiliki turunan yang kontinu dalam R, maka: 1. = tidak tergantung pada lintasan C dalam R yang menghubungkan p 1 dan p 2 2. mengelilingi setiap kurva tertutup C dalam R. Dalam hal demikian A disebut sebuah medan vektor konservatif dan Φ adalah potensial skalarnya. jadi sebuah medan vektor A adalah konservatif jika dan hanya jika x. A=0, atau juga ekivalen dengan A= Φ.

Contoh: 1. Diketahui F=( 2 xy+z 3 ) i + x 2 j+3 x z 2 k a. tunjukan bahwa F sebuah medan gaya konservatif b. carilah potensial skalar c. carilah usaha yang dilakukan dalam menggerakan sebuah benda dalam. Medan ini dari (1, -2, 1) ke (3, 1, 4). Jawab: a. Syarat perlu dan cukup agar sebuah daya konservatif adalah Curl F= xf=0

b. integrasikan (1), (2), dan (3), diperoleh masing-masing Dengan memilih F(y, z)=0, G(x, z)=xz 3 dan H(x, y) =x 2 y, maka diperoleh: Φ=x 2 y +x z 3 dengan tambahan sembarang konstanta.

c.

Contoh: Jika A = ( 4 x y – 3 k 2 z 2 ) i + 2 x 2 j – 2 x 3 z k Buktikan bahwa tidak tergantung lintasan c yang menghubungkan dua titik. Jawab : Jika tidak tergantung lintasan , maka A adalah medan konservatif. Kalau A medan konservatif , maka akan berlaku x A = 0. x. A = = i ( 0 ) – j ( - 6 x 2 z + 6 x 2 z ) + k ( 4 x – 4 x ) = 0

TEOREMA GREEN DALAM BIDANG 1. Teorema Green Dalam Bidang Jika R adalah suatu daerah tertutup dalam bidang xy yang dibatasi oleh kurva tertutup C dan jika M dan N adalaj fungsi-fungsi kontinu dari x dan y yang memiliki turunan-turunan kontinu dalam R, maka dimana C dilintasi dalam arah positif (berlawanan arah putaran jarum jam). Bila tidak ada pernyataan lain, kita akan selalu menganggap berarti bahwa integeralnya dimaksud dalam arah positif.

Contoh : Hitunglah (xy + y 2)dx + x 2 dy, dimana C adalah kurva tertutup dari daerah yang dibatasi oleh y = x dan y = x 2 dengan menggunakan teorema Green dalam bidang. Jawab: = =
 Flux surface integral
Flux surface integral Mendiferensiasikan
Mendiferensiasikan Contoh ayat bertolak ansur
Contoh ayat bertolak ansur Garis tinggi segitiga
Garis tinggi segitiga Garis px dan garis berpotongan dengan garis
Garis px dan garis berpotongan dengan garis Kita akan tetap saling memiliki walau jarak
Kita akan tetap saling memiliki walau jarak Sifat-sifat yang dimiliki abu lahab
Sifat-sifat yang dimiliki abu lahab Integral vs definite integral
Integral vs definite integral Integral and non integral citation
Integral and non integral citation Blair matthews
Blair matthews Integral foreign operation meaning
Integral foreign operation meaning Udv integral
Udv integral Jangka tolok digunakan untuk mengukur
Jangka tolok digunakan untuk mengukur Persamaan garis yang menyinggung kurva y=x3-4x2-3x-5
Persamaan garis yang menyinggung kurva y=x3-4x2-3x-5 Materi integral garis
Materi integral garis Teorema dasar integral garis
Teorema dasar integral garis Contoh soal integral garis dan penyelesaiannya
Contoh soal integral garis dan penyelesaiannya Balok klmn opqr diiris menurut rusuk-rusuk
Balok klmn opqr diiris menurut rusuk-rusuk Garis singgung luar
Garis singgung luar