Jos Antonio Weymann POINT LINE AND PLANE Point

José Antonio Weymann

POINT, LINE AND PLANE Point: A single dot in space, used to describe location. It is described with a dot and a capital letter. P Line: A straight connection of points that goes on forever in both directions. XY YX Plane: A flat surface that goes on forever, it has no thickness and it contains 3 points. T

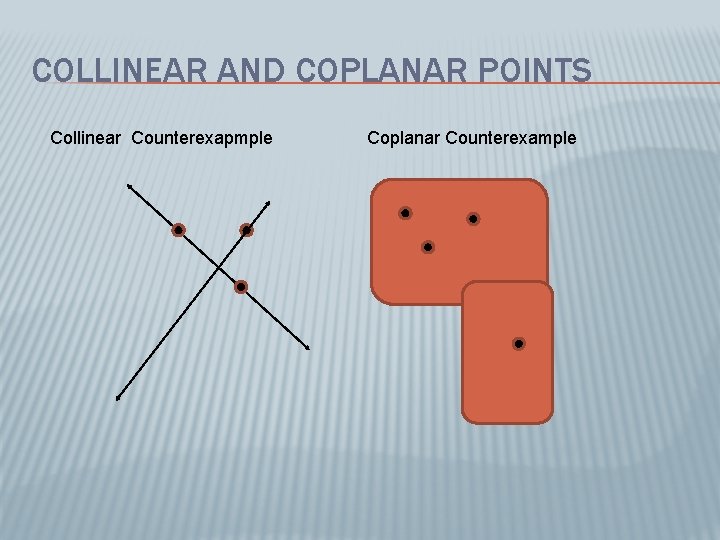
COLLINEAR AND COPLANAR POINTS � The difference between collinear and coplanar points is collinear points coexist in in the same line and coplanar points coexist in the same plane. Collinear Coplanar: P N A B M

COLLINEAR AND COPLANAR POINTS Collinear Counterexapmple Coplanar Counterexample

LINE, SEGMENT, AND RAY Line: A straight connection of points that goes on forever in both directions. XY YX Segment: Any straight collection of dots that has a beginning and an end (endpoints) XY Ray: A straight collection of points that has one end point and goes on forever. XY *This are related because they all are ways to use points and lines, also we will be using them for the rest of the school year. Besides their everyday location and distance

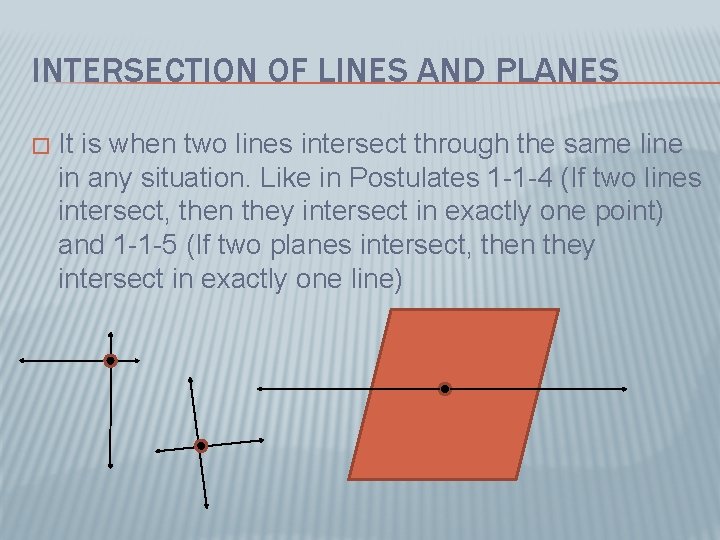
INTERSECTION OF LINES AND PLANES � It is when two lines intersect through the same line in any situation. Like in Postulates 1 -1 -4 (If two lines intersect, then they intersect in exactly one point) and 1 -1 -5 (If two planes intersect, then they intersect in exactly one line)

POSTULATE, AXIOM AND THEOREM � The Difference between Postulate, Axiom and Theorem is between Postulate and Axiom is nothing they are interchangeable terms (this are accepted truths as fact with out proof), but between this and theorem is that a theorem is a theoretical proposition, later to be proved by other propositions and formulas.

RULER POSTULATE (POSTULATE 1 -2 -1) � � � To measure segments use a ruler and just subtract the values at the end points. A Field is 120 ft long and a player starts running from 60 ft , what is the distance when he runs to point 120 ft? Answer: 60 ft, The road is 130 km long and a car starts its trip from south park which is 90 km up the road, when he reaches the 130 km line how many km does the car have traveled? Answer: 40 km The sidewalk is 850 mt long and an old lady starts walking from 500 mt, when she reaches the end of the sidewalk, what’s her current distance Answer: 350 mt.

SEGMENT ADDITION POSTULATE (1 -2 -2) � If A, B, C (our three collinear points) and B is between A & C, then AB+BC=AC 24 � C 46 A B 24+46= 70, so CB C 72+20= 92, so AC = 70 so CA+AB= CB 72 A B � 20 = 92 � E so AB+BC=AC 75 F 55 G 75+55= 130, so EG =

DISTANCE BETWEEN TWO POINTS ON A COORDINATE PLANE � To find the distance between two points on a coordinate plane you have to take the X 1 and X 2 coordinates and square them then the Y 1 & Y 2 coordinates and do the same, add and then square the answer. d = √ (X₁-X₂)₂+(Y₁ -Y₂)₂ � AB= √(5 -0)₂+(1 -3)₂ * CD= √(-3 –(-1)₂+(-4 - 1)₂ √ 5₂ + (-2)₂ √(-2)₂+(-5)₂ √ 25+ 4 √ 4+25 This are congruent √ 29 d= √(4 -1)₂+(2 -6)₂ √ 3₂+(-4)₂ √ 9+16 √ 25 = 5 this is a random problem

CONGRUENCE AND EQUALITY � Congruence means and equal measure, not necessarily a value, we are comparing names; this contrasts with equality because that means 2 things with same value, therefore it is comparing values. They are similar because both are comparing two things. They are different because congruent is two objects exactly the same regardless of orientation, and equality is shape size and angles, like two squares they are congruent but don’t have measurements meaning we don’t know if they are equal. ≈ =

PYTHAGOREAN THEOREM (THEOREM 1 -6 -1) � In a right triangle, the sum of the squares of the lengths of the legs is equal to the square of the length of the hypotenuse. a₂+b₂=c₂ � a=4 and b=5 c₂= a₂+b₂ =4₂+5₂ =16+25 =41 c=√ 41 c≈ 6. 4 a=3 and b=4 find the value of c c₂= a₂+b₂=c₂ a=4 b=5 = 3₂+4₂ 4₂+5₂= c₂ =9+16 16+25= c₂ =25 41= c₂ c=√ 25 c≈ 5

ANGLES � Angles are 2 rays that share a common end point. There acute (smaller than 90°), right (90°), obtuse (bigger than 90°) and finally straight angles (180°) Right Acute Obtuse Straight Exterior Interior

ANGLE ADDITION POSTULATE (1 -3 -2) � 2 small angles add up to the big angle. 1. angle ABD=150 2. angle EFI=180 3. angle VXY=110 angle ABC=45 angle FGI=90 angle YXZ=60 150 -45= 180 -90= 110+60= CBD=105 EFG=90 VXY=170

MIDPOINT (CONSTRUCTION AND MIDPOINT FORMULA) � Midpoint is what we call the middle of the segment, equidistant from the endpoints; cuts into two equal smaller segments. To construct a midpoint first draw a segment, second draw a line a little bit passed the approximate middle, third draw two arcs from both endpoints in the two sides of the segment, fourth draw a straight line through the crossings and you have your constructed midpoint. MIDPOINT FORMULA: (X₁+X₂/2, Y₁+Y₂/2) 1. (6+4)(4+1)/2 m=1. 5 2. (-3+0)(-1, 1)/2 m=-1. 5 3. (-3+-1. 5)(4+1)/2 m= -. 75, 2. 5

ANGLE BISECTOR (CONSTRUCTION) � An angle bisector is a line which cuts and angle into two equal parts, therefore the word bisect means to cut in have. First lock your compass, make an arc in each side put the point in each arc and make an arc in the interior; then connect the vertex to the intersection point.

ADJACENT, VERTICAL AND LINEAR PAIRS Adjacent: are 2 angles that have the same vertex and a same side. � Linear Pairs of Angles: 2 adjacent straight angles that will form a straight line. Meaning all Linear Pairs of Angles are supplementary (Linear Pair Postulate, L. P. P) � Vertical: Non adjacent angles formed when 2 lines intersect; vertical angles are always congruent. Adjacent: Linear Pairs: Vertical: �

COMPLEMENTARY AND SUPPLEMENTARY Complementary angles are 2 angles that add up to 90º and supplementary add up to 180º; supplementary are always linear pairs but complementary aren`t, they are always adjacent. � Complementary: 90º Supplementary: 180º �

PERIMETER AND AREA Square: to take the perimeter of a square add all 4 sides (P=4 s) and area just square one side (A=s₂) � Rectangle: to take the perimeter of a rectangle add the 2 lengths and 2 widths (P=2 l+2 w) and area multiply length time width (A=lw) � Triangle: to take the perimeter of a triangle (a+b+c) and to take the area (bh/2) Square: P=4(4), P=16 ft. Rectangle: 5 ft. 4 ft. A=4₂, A= 16 ft₂ 4 ft. � P=5+5+4+4, P=18 ft. A=5*4, A=20 ft. ₂

PERIMETER AND AREA Triangle: P= 2 x+3 x+5+10 A=1/2(3 x+5)(2 x) = 5 x+15 =3 x₂+5 x 2 nd round of examples: Square: Rectangle: P=6(4) P=24 A= 6₂ A= 36 3 cm. 5 cm. P=3+3+5+5 P= 16 cm. A=3*5 A=15 cm. ₂ Triangle: P=4 x+5 x+3+9 A=1/2(5 x+9)(4 x) = 9 x+12 =5 x₂+5 x

CIRCUMFERENCE OF A CIRCLE The circumference of a circle is the distance around the circle. Circumference (C) is given by C=(Pi)d or C=2(Pi)r =2(Pi)(3)=6(Pi) =2(Pi)(11) ≈ 18. 8 cm =22(Pi) ≈69. 1 cm. � 3 cm. 11 cm.

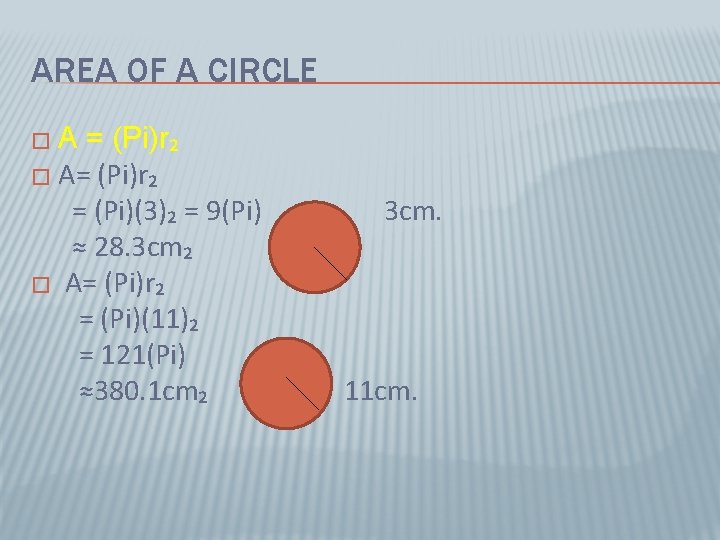
AREA OF A CIRCLE �A = (Pi)r₂ � A= (Pi)r₂ = (Pi)(3)₂ = 9(Pi) ≈ 28. 3 cm₂ � A= (Pi)r₂ = (Pi)(11)₂ = 121(Pi) ≈380. 1 cm₂ 3 cm. 11 cm.

FIVE STEP PROBLEM SOLVING PROCESS � 1. READ IT CAREFULLY 2. WRITE DOWN ALL IMPORTANT INFORMATION 3. DRAW A PICTURE 4. WRITE AND SOLVE THE EQUATION 5. ANSWER THE QUESTION

FIVE STEP PROBLEM SOLVING PROCESS 1. Read it Carefully: The quilt pattern includes 32 small triangles. Each has a base of 3 inches and a height of 1. 5 in. Find the amount of fabric used to make the 32 triangles. 2. Write down all important information: 3 inches, 32 small triangles, 1. 5 inches 3. Draw a Picture h: 1. 5 in. � b:

FIVE STEP PROBLEM SOLVING PROCESS 4. Write and Solve the equation b: 3 in. h: 1. 5 in. bh/2 (3)(1. 5)/2 *32 = 72 5. Answer the Question Answer: The amount of fabric used to make the 32 triangles in the quilt is 72 in₂

INTRODUCTION TO TRANSFORMATIONS � Things to know before entering transformations Pre-image: Image: A A ABC A’B’C’

TRANSFORMATIONS A Transformation is a change in the position of the original object. � Translation : The slide of an object in any direction (usually is the most common) (X, Y) (X+a, Y+b) �

TRANSFORMATIONS � Rotation: to rotate a figure around a point.

TRANSFORMATIONS � Reflection: When you mirror your Pre-image across any line. If across Y-axis (X, Y)(-X, Y). If across Xaxis (X, Y)(X, -Y)

JOURNAL HAS BEEN CONCLUDED � This geometry chapter 1 journal has ended, good luck on the quiz and I hope to have covered the topics In a satisfactory matter.