Lesson 1 1 Point Line Plane Modified by

Lesson 1 -1 Point, Line, Plane Modified by Lisa Palen

1 -1 Part A - Geometry : The Objects Point, Line, Plane, Segment, Ray, Angle

Undefined Terms • Point • Line • Plane We describe these, rather than defining them.

Point • A place in space. Has no actual size. • How to Sketch: Use dots • How to label: Use capital printed letters Never name two points with the same letter (in the same sketch). A B C A

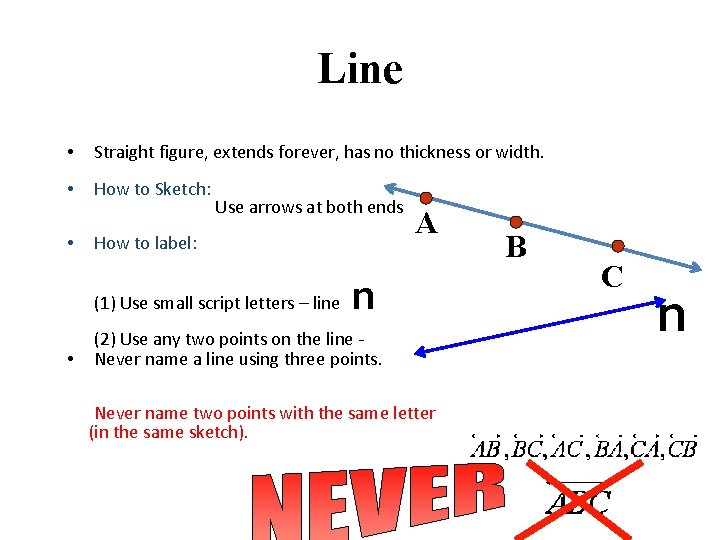
Line • Straight figure, extends forever, has no thickness or width. • How to Sketch: • Use arrows at both ends How to label: (1) Use small script letters – line • A n (2) Use any two points on the line Never name a line using three points. Never name two points with the same letter (in the same sketch). B C n

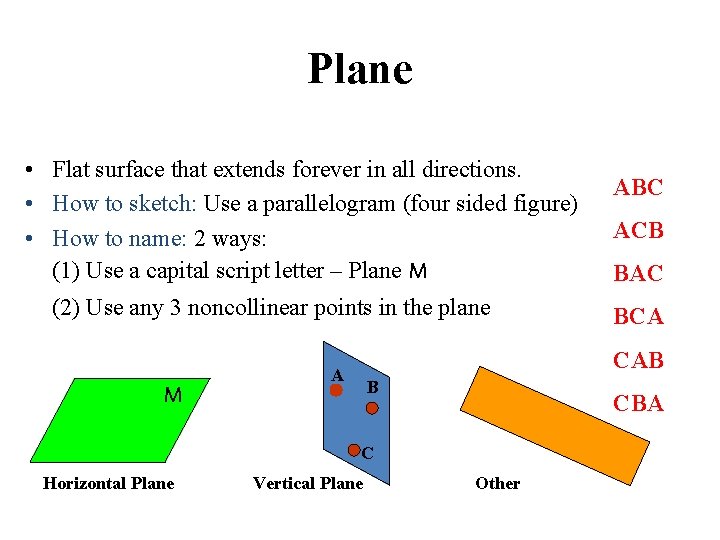
Plane • Flat surface that extends forever in all directions. • How to sketch: Use a parallelogram (four sided figure) • How to name: 2 ways: (1) Use a capital script letter – Plane M (2) Use any 3 noncollinear points in the plane M ACB BAC BCA CAB A B CBA C Horizontal Plane ABC Vertical Plane Other

More Objects • Segment • Ray • Angle

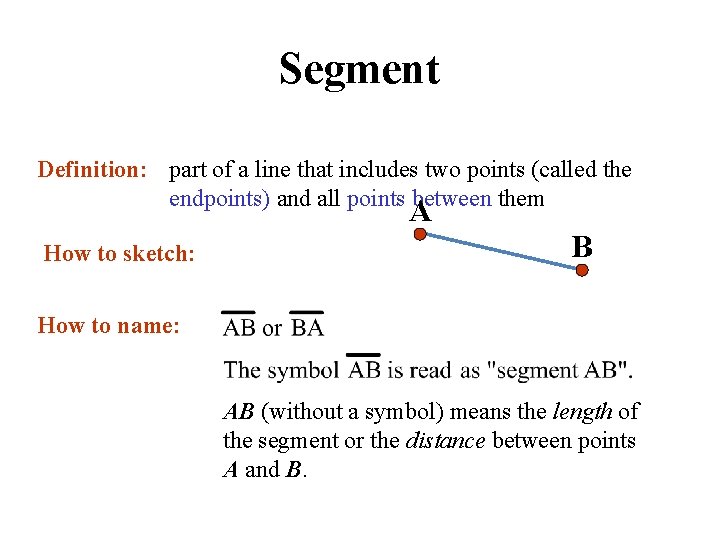
Segment Definition: part of a line that includes two points (called the endpoints) and all points between them A How to sketch: B How to name: AB (without a symbol) means the length of the segment or the distance between points A and B.

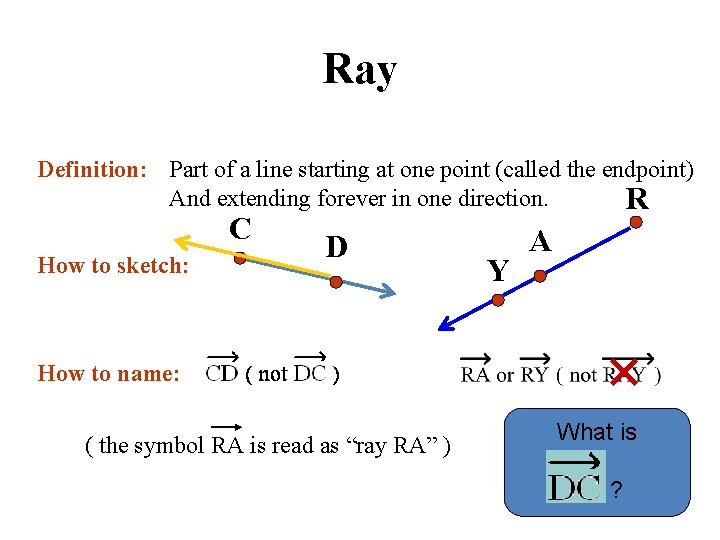
Ray Definition: Part of a line starting at one point (called the endpoint) And extending forever in one direction. R C How to sketch: D Y A How to name: ( the symbol RA is read as “ray RA” ) What is ?

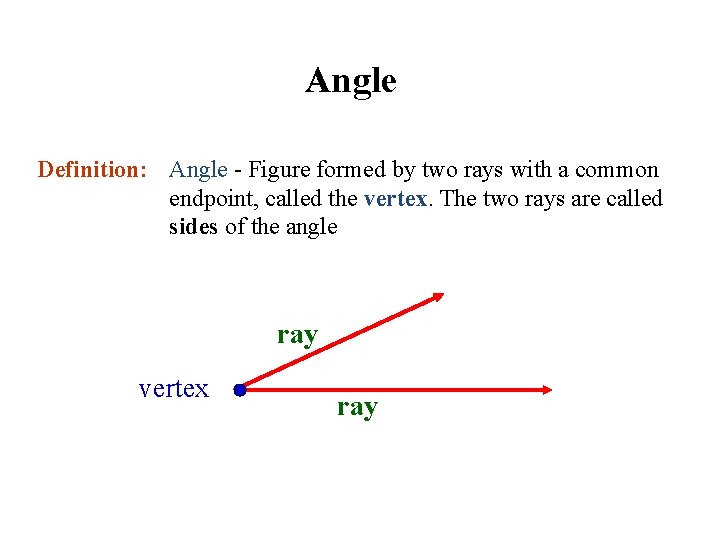
Angle Definition: Angle - Figure formed by two rays with a common endpoint, called the vertex. The two rays are called sides of the angle ray vertex ray

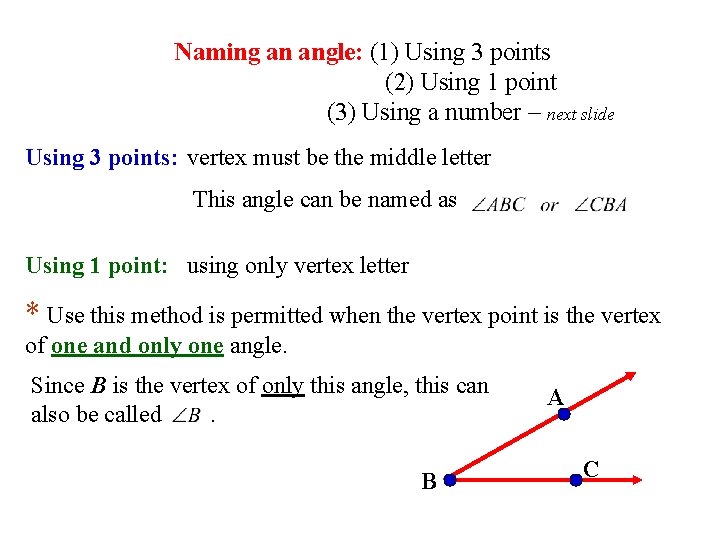
Naming an angle: (1) Using 3 points (2) Using 1 point (3) Using a number – next slide Using 3 points: vertex must be the middle letter This angle can be named as Using 1 point: using only vertex letter * Use this method is permitted when the vertex point is the vertex of one and only one angle. Since B is the vertex of only this angle, this can also be called. B A C

Naming an Angle - continued Using a number: A number (without a degree symbol) may be used as the label or name of the angle. This A number is placed in the interior of the angle near its vertex. The angle to the left can be named B 2 C as. * The “ 1 letter” name is unacceptable when … more than one angle has the same vertex point. In this case, use three letter name or a number if it is present.

Example l K is the vertex of more than one angle. Therefore, there is NO There are in this diagram. .

Lesson 1 -1 Part B Vocabulary Collinear, Coplanar, Intersection, Intersect, Parallel, Perpendicular Modified by Lisa Palen

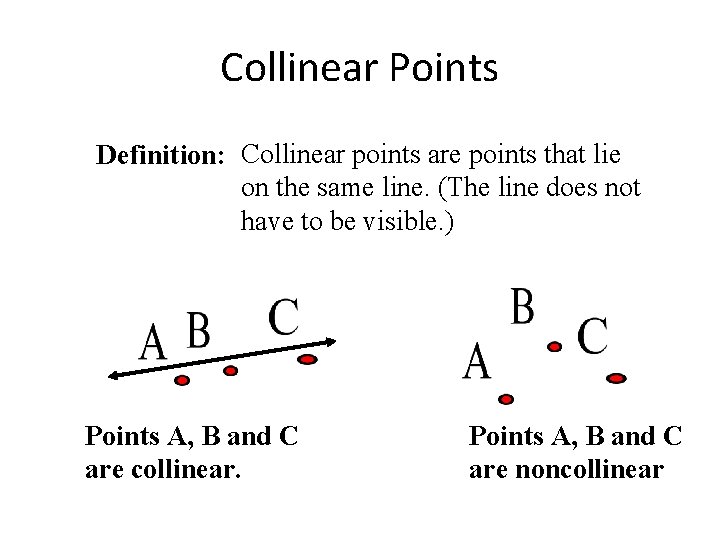
Collinear Points Definition: Collinear points are points that lie on the same line. (The line does not have to be visible. ) Points A, B and C are collinear. Points A, B and C are noncollinear

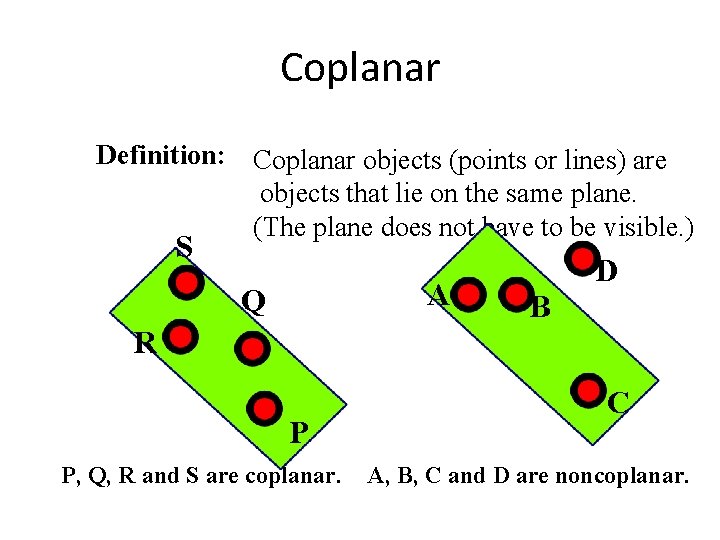
Coplanar Definition: Coplanar objects (points or lines) are objects that lie on the same plane. (The plane does not have to be visible. ) S A Q D B R P P, Q, R and S are coplanar. C A, B, C and D are noncoplanar.

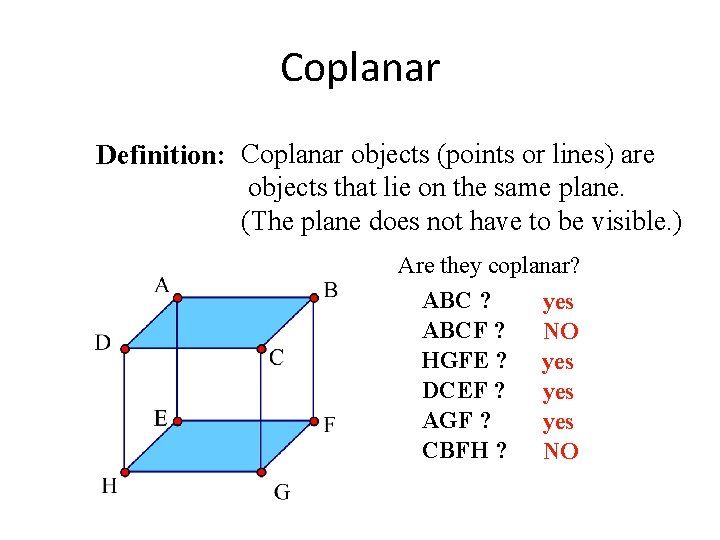
Coplanar Definition: Coplanar objects (points or lines) are objects that lie on the same plane. (The plane does not have to be visible. ) Are they coplanar? ABC ? yes ABCF ? NO HGFE ? yes DCEF ? yes AGF ? yes CBFH ? NO

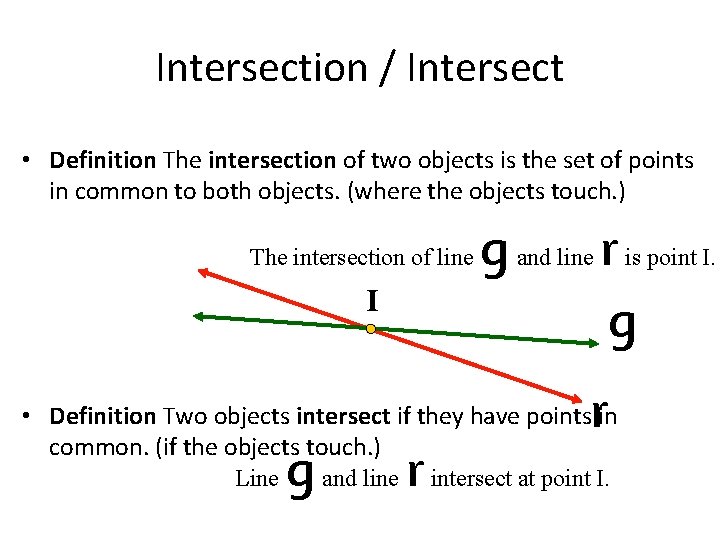
Intersection / Intersect • Definition The intersection of two objects is the set of points in common to both objects. (where the objects touch. ) r I g • Definition Two objects intersect if they have pointsrin common. (if the objects touch. ) g r The intersection of line Line and line g and line intersect at point I. is point I.

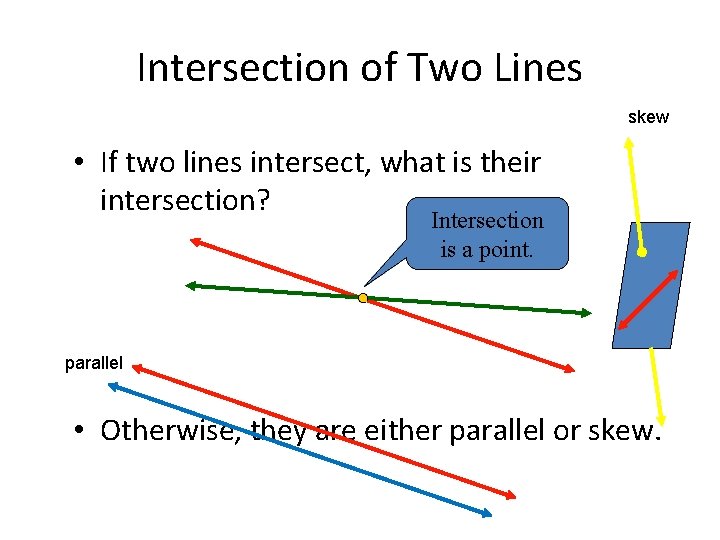
Intersection of Two Lines skew • If two lines intersect, what is their intersection? Intersection is a point. parallel • Otherwise, they are either parallel or skew.

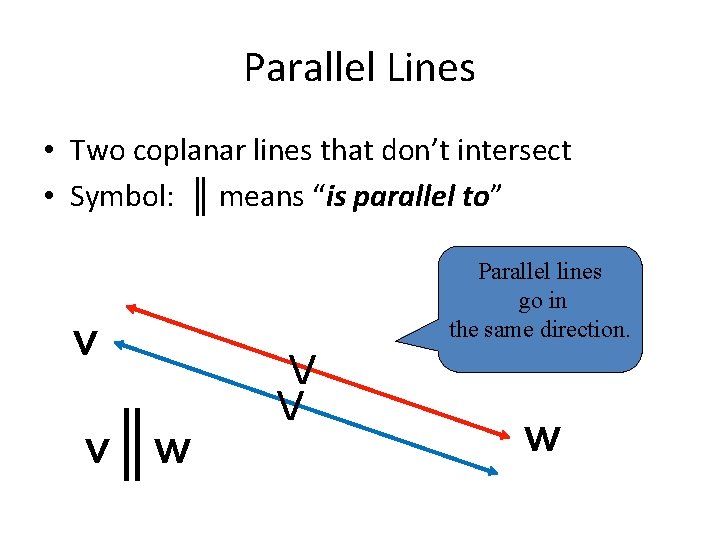
Parallel Lines • Two coplanar lines that don’t intersect • Symbol: ║ means “is parallel to” v v║w Parallel lines go in the same direction. V V w

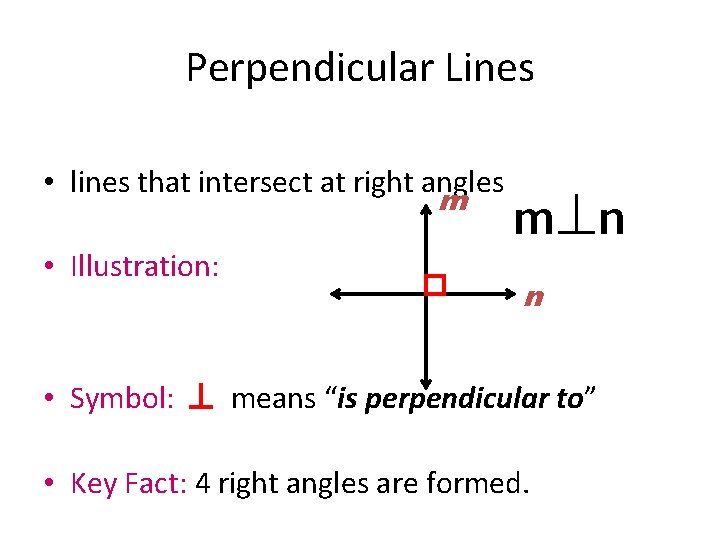
Perpendicular Lines • lines that intersect at right angles m • Illustration: m n n • Symbol: means “is perpendicular to” • Key Fact: 4 right angles are formed.

Lesson 1 -2 Segments and Rays Modified by Lisa Palen

Recall: What is a Segment? Definition: two points (called the endpoints) and all points between them A How to sketch: How to name: B

Measure (of a Segment) Definition: The length of the segment or the distance between the two endpoints A The measure of is AB. Recall: The symbol A B”. Notation: B is read as “segment AB (without a symbol) means the length of the segment or the distance between points A and B.

Congruent Segments Definition: Congruent segments are segments with equal measures (lengths). Mark congruent segments with. . dashes. . Congruent segments have the same number of dashes. Notation: The symbol congruent to”. means “is E F G H

Congruent Segments Using the Notation: Numbers are equal. Objects are congruent. AB: the distance from A to B ( a number ) AB: the segment AB ( an object ) Correct notation: Incorrect notation:

Midpoint Definition: A midpoint is a point that divides a segment into two congruent segments. E is the midpoint of and . DE = EF

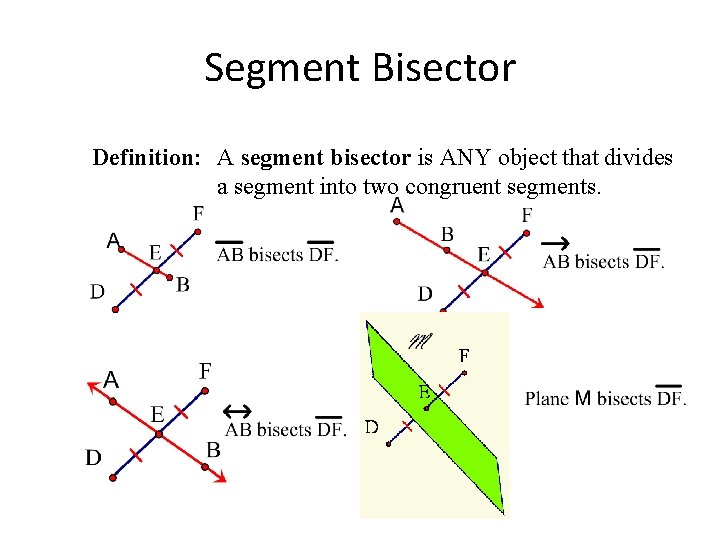
Segment Bisector Definition: A segment bisector is ANY object that divides a segment into two congruent segments.

Postulates Definition: a statement we accept as true without proof. Examples: • Through any two points there is exactly one line. • Through any three non-collinear points, there is exactly one plane.

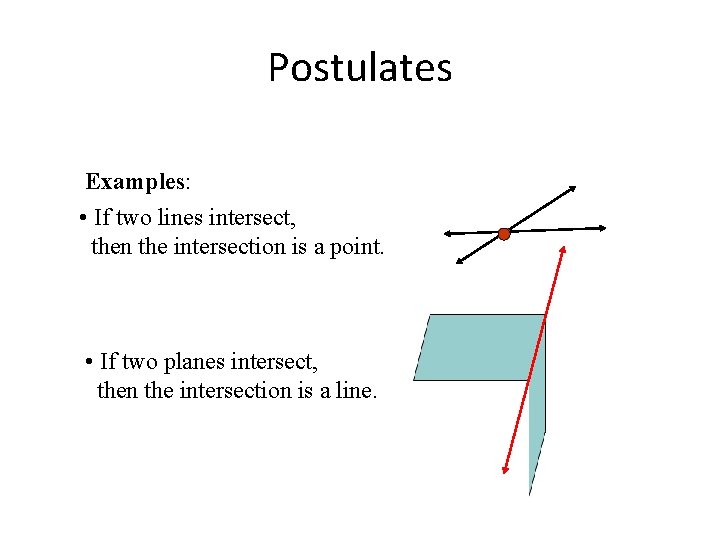
Postulates Examples: • If two lines intersect, then the intersection is a point. • If two planes intersect, then the intersection is a line.

The Ruler Postulate The points on any line can be paired with the real numbers in such a way that: The Ruler Postulate says youpoints can use a paired ruler with to 0 and 1. • Any two chosen can be • The distancemeasure between any twodistance points in a number line is the absolute value of the difference of the real numbers between any two points! corresponding to the points. (It also gives us a. formula. )

The Ruler Postulate • So, we can measure the distance between two points using a “ruler”. • Formula: take the absolute value of the difference of the two coordinates a and b: │a – b │ | | PK = 3 - -2 = 5 (distance is always positive)

Reminder • The coordinates are the numbers on the ruler or number line! • The capital letters are the names of the points. • Coordinates: -3, -2, -1, 0, 1, 2, 3, etc. • Points: G, H, I, J, etc.

Another Example Find the distance between I and S. Coordinate of I: -4 Coordinate of S: 6 Take the absolute value of the difference: │a – b │ │ -4 - 6 │= │ - 10 │ = 10

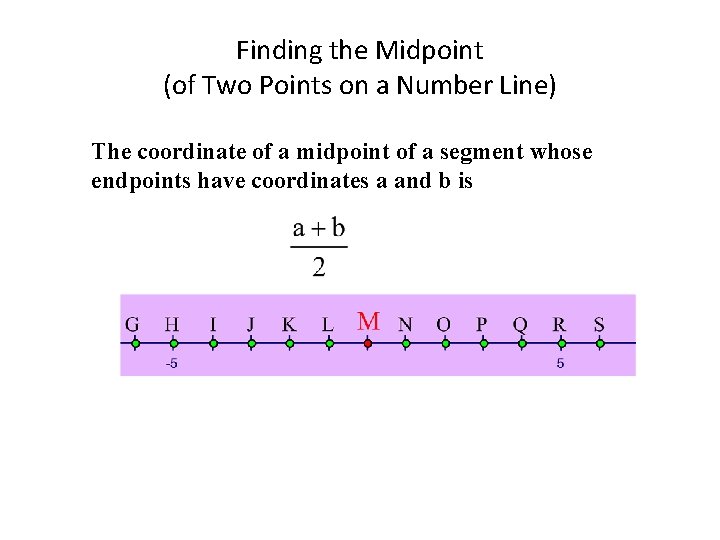
Finding the Midpoint (of Two Points on a Number Line) The coordinate of a midpoint of a segment whose endpoints have coordinates a and b is

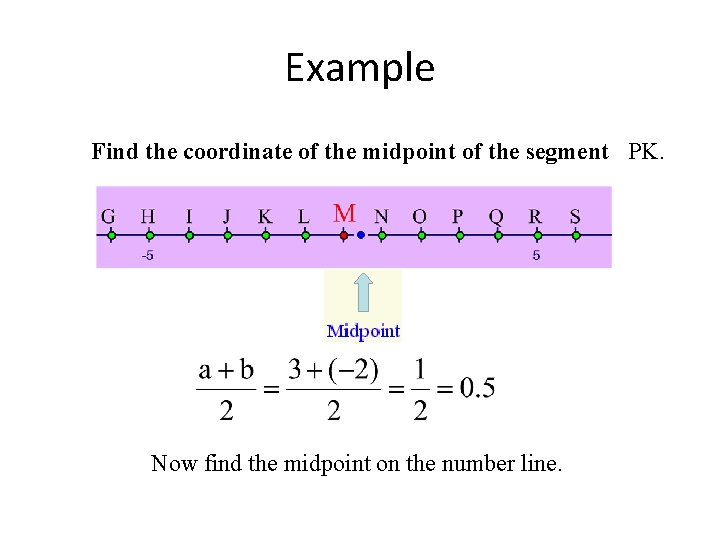
Example Find the coordinate of the midpoint of the segment PK. Now find the midpoint on the number line.

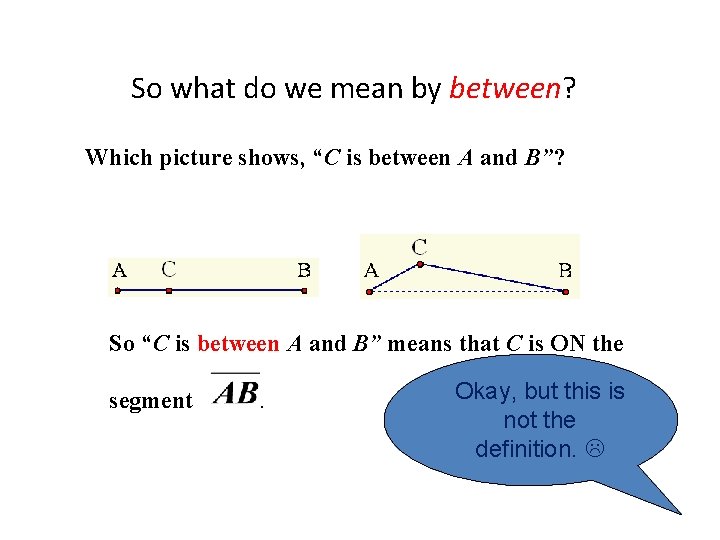
So what do we mean by between? Which picture shows, “C is between A and B”? So “C is between A and B” means that C is ON the segment . Okay, but this is not the definition.

Between or The Segment Addition Postulate Definition: • If C is between A and B, then AC + CB = AB. • If AC + CB = AB, then C is between A and B. AC + CB = AB between AC + CB > AB not between This is also called the Segment Addition Postulate.

The Segment Addition Postulate (This is the same as “between. ” ) In Other Words: Or: The whole is the sum of the parts. Part + Part = Whole These are the same length.

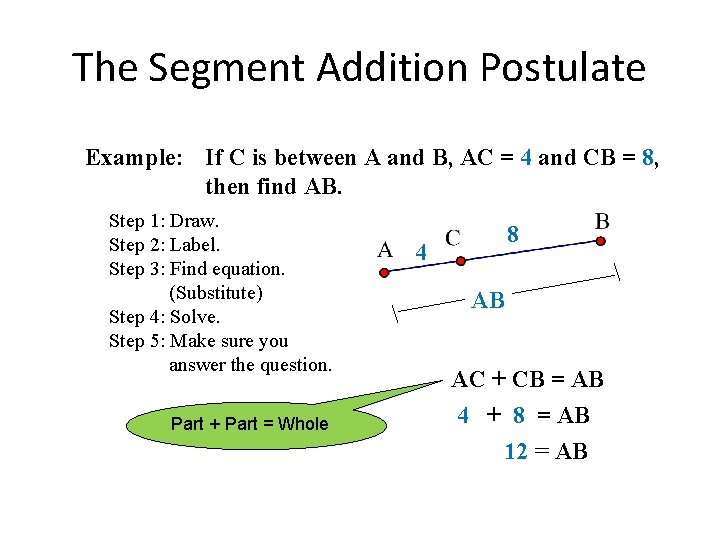
The Segment Addition Postulate Example: If C is between A and B, AC = 4 and CB = 8, then find AB. Step 1: Draw. Step 2: Label. Step 3: Find equation. (Substitute) Step 4: Solve. Step 5: Make sure you answer the question. Part + Part = Whole 8 4 AB AC + CB = AB 4 + 8 = AB 12 = AB

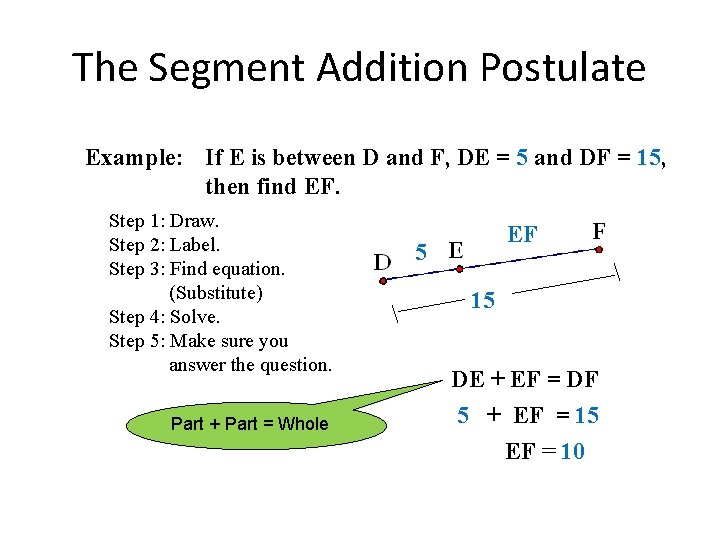
The Segment Addition Postulate Example: If E is between D and F, DE = 5 and DF = 15, then find EF. Step 1: Draw. Step 2: Label. Step 3: Find equation. (Substitute) Step 4: Solve. Step 5: Make sure you answer the question. Part + Part = Whole EF 5 15 DE + EF = DF 5 + EF = 15 EF = 10

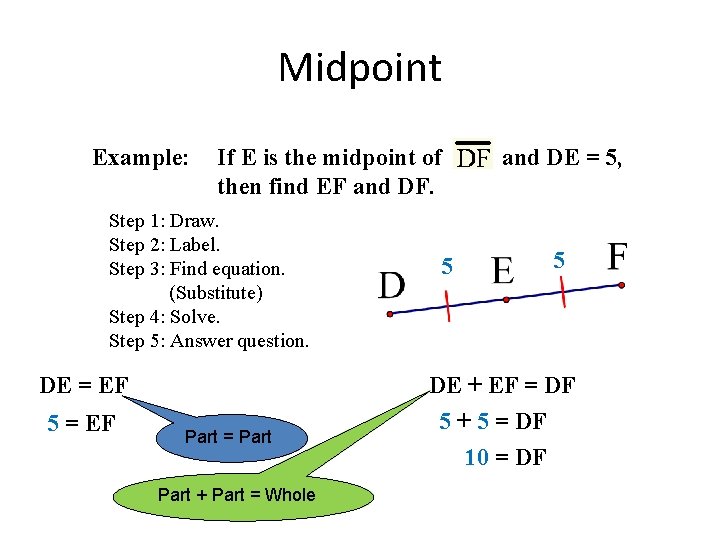
Midpoint Example: If E is the midpoint of then find EF and DF. Step 1: Draw. Step 2: Label. Step 3: Find equation. (Substitute) Step 4: Solve. Step 5: Answer question. DE = EF 5 = EF , and DE = 5, 5 5 DE + EF = DF Part = Part + Part = Whole 5 + 5 = DF 10 = DF

Lesson 1 -4 Angles

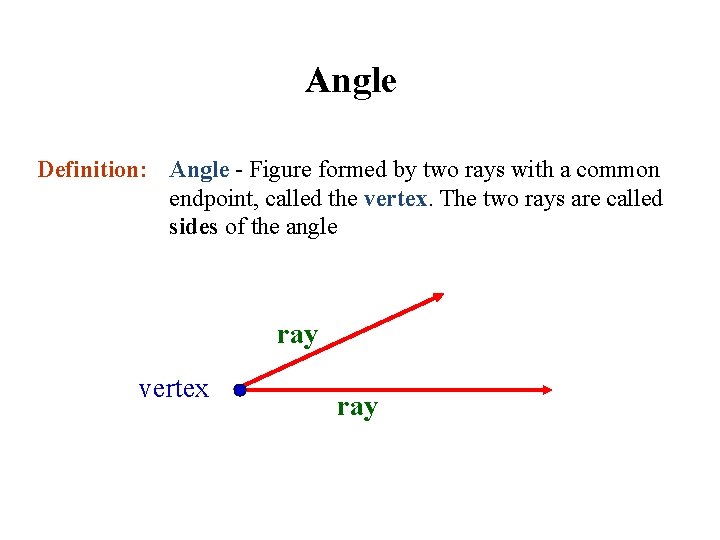
Angle Definition: Angle - Figure formed by two rays with a common endpoint, called the vertex. The two rays are called sides of the angle ray vertex ray

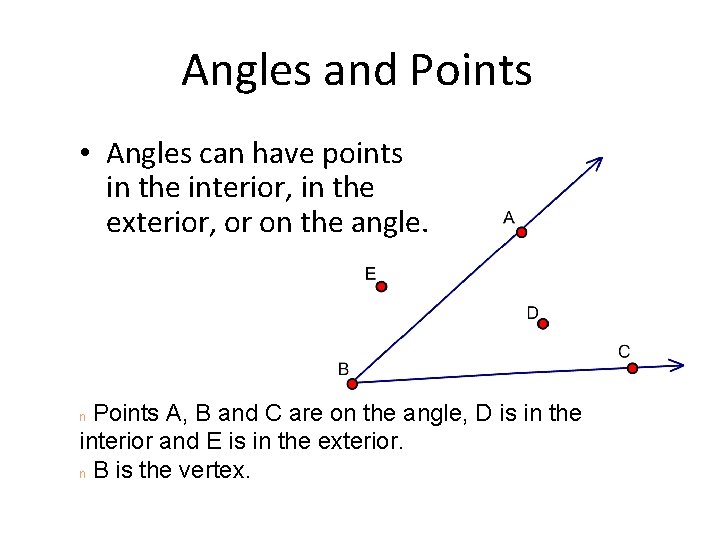
Angles and Points • Angles can have points in the interior, in the exterior, or on the angle. Points A, B and C are on the angle, D is in the interior and E is in the exterior. n B is the vertex. n

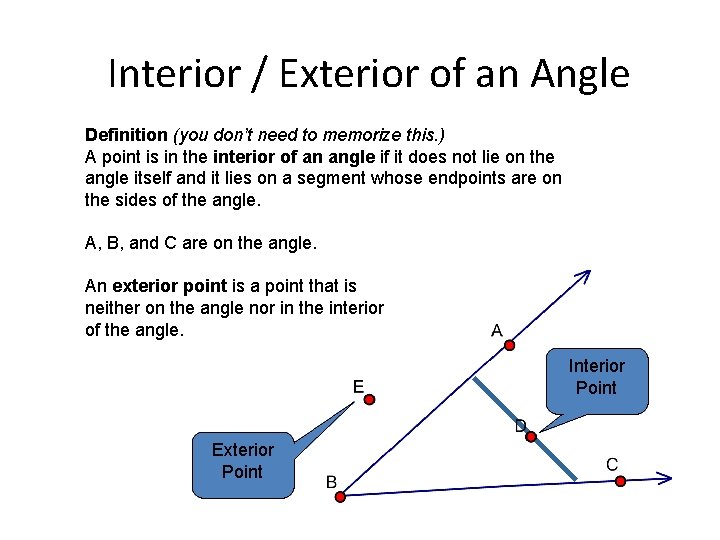
Interior / Exterior of an Angle Definition (you don’t need to memorize this. ) A point is in the interior of an angle if it does not lie on the angle itself and it lies on a segment whose endpoints are on the sides of the angle. A, B, and C are on the angle. An exterior point is a point that is neither on the angle nor in the interior of the angle. Interior Point Exterior Point

The Protractor Postulate You don’t need to memorize this! Given a. The ray AB and a Protractor Postulate number r between 0 and 180, says you can use a there is exactly one raytowith protractor measure endpoint A extending to angles! either side of AB, such that the measure of the angle formed is r degrees.

The Ruler and Protractor Postulates The Ruler Postulate lets us use a ruler to measure the distance between two points. The Protractor Postulate lets us use a protractor to measure an angle. . Protractor Applet

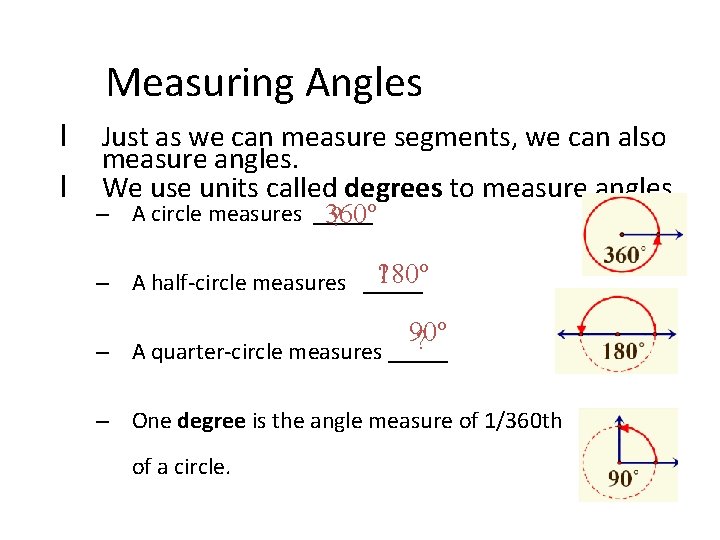
Measuring Angles l l Just as we can measure segments, we can also measure angles. We use units called degrees to measure angles. – A circle measures _____ 360º ? ? 180º – A half-circle measures _____ 90º ? – A quarter-circle measures _____ – One degree is the angle measure of 1/360 th of a circle.

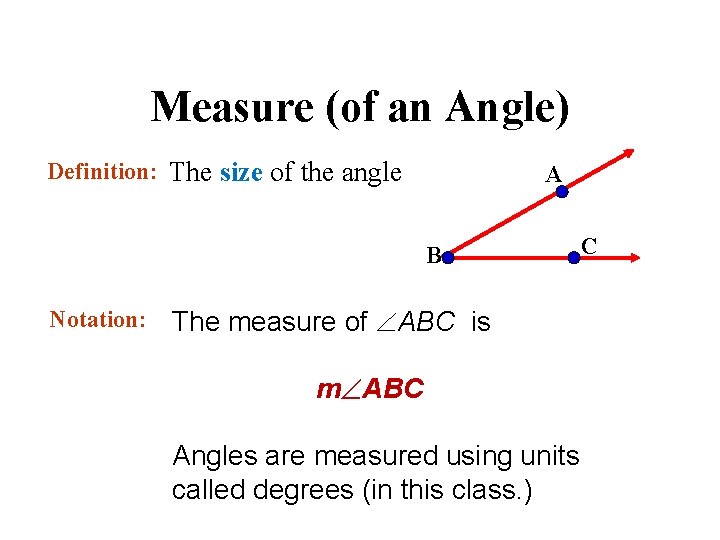
Measure (of an Angle) Definition: The size of the angle A B Notation: The measure of ABC is m ABC Angles are measured using units called degrees (in this class. ) C

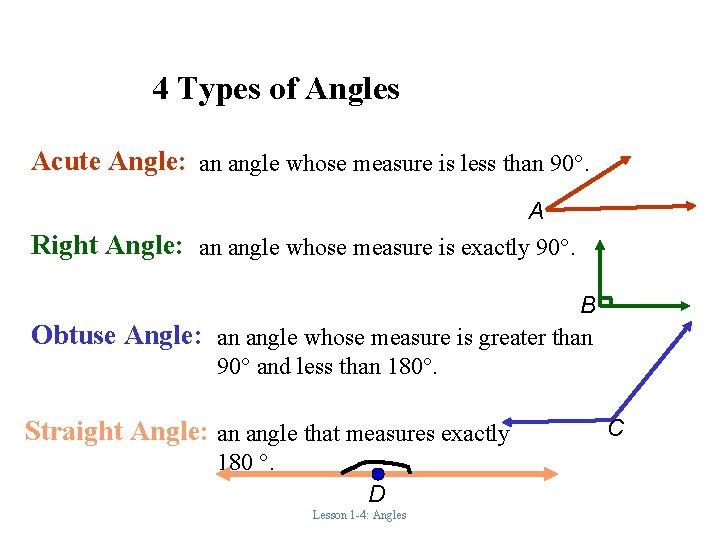
4 Types of Angles Acute Angle: an angle whose measure is less than 90. A Right Angle: an angle whose measure is exactly 90. B Obtuse Angle: an angle whose measure is greater than 90 and less than 180. Straight Angle: an angle that measures exactly C 180 . D Lesson 1 -4: Angles 56

Congruent Angles Definition: Congruent angles - angles that have equal measures Congruent angles are marked with the same number of “arcs”. The symbol for congruence is Example: 4 2 2 4. Lesson 1 -4: Angles 57

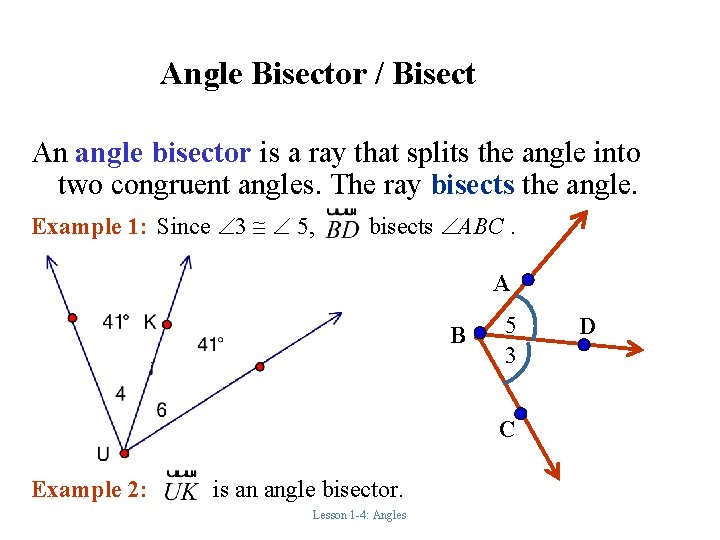
Angle Bisector / Bisect An angle bisector is a ray that splits the angle into two congruent angles. The ray bisects the angle. Example 1: Since 3 5, bisects ABC. A B 5 3 D C Example 2: is an angle bisector. Lesson 1 -4: Angles 58

Example 1 Angle Bisector If is an angle bisector of PMY and m PML = 68 , then find: • m PMY = _______ • m LMY = _______

Example 2 Angle Bisector If is an angle bisector of PMY and m PMY = 86 , then find: • m PML = _______ • m LMY = _______

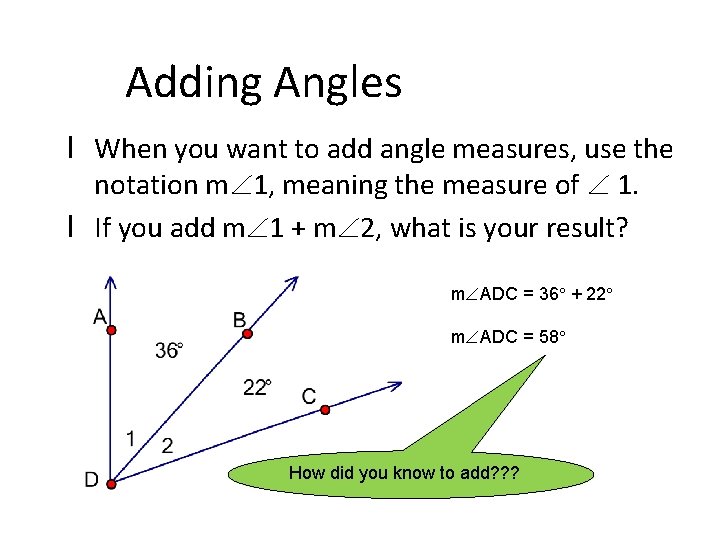
Adding Angles l When you want to add angle measures, use the notation m 1, meaning the measure of 1. l If you add m 1 + m 2, what is your result? m ADC = 36 + 22 m ADC = 58 How did you know to add? ? ?

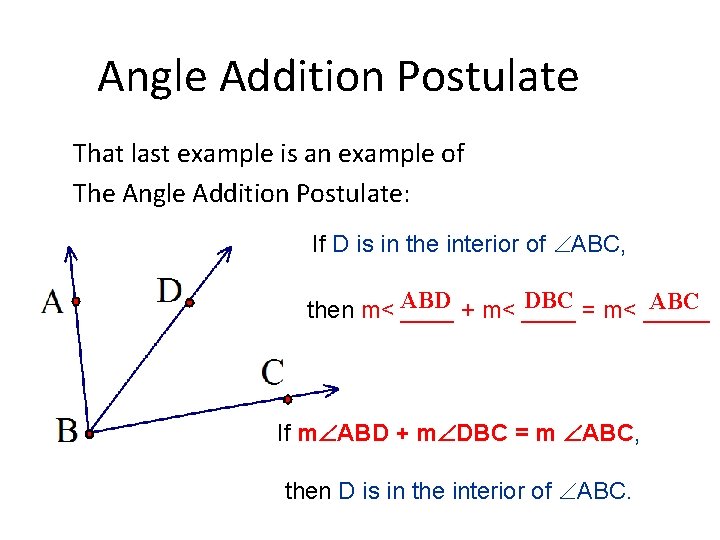
Angle Addition Postulate That last example is an example of The Angle Addition Postulate: If D is in the interior of ABC, DBC = m< _____ ABC then m< ABD ____ + m< ____ If m ABD + m DBC = m ABC, then D is in the interior of ABC.

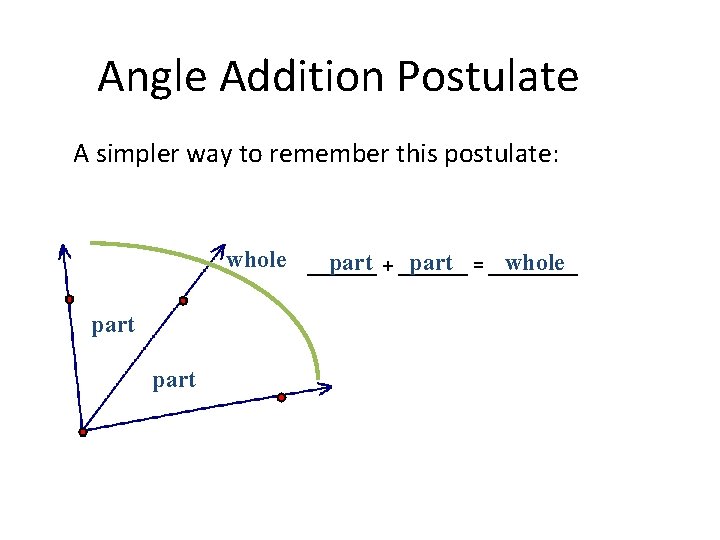
Angle Addition Postulate A simpler way to remember this postulate: whole part + _______ part = _____ whole _______

Lesson 1 -5 Pairs of Angles Lesson 1 -5: Pairs of Angles 65

Adjacent Angles Definition: A pair of coplanar angles with a common (shared) vertex and common side that do not have overlapping interiors. Examples: 1 and 2 are adjacent. 3 and 4 are not. 1 and ADC are not adjacent. 4 3 Adjacent Angles( a common side ) Lesson 1 -5: Pairs of Angles Non-Adjacent Angles 66

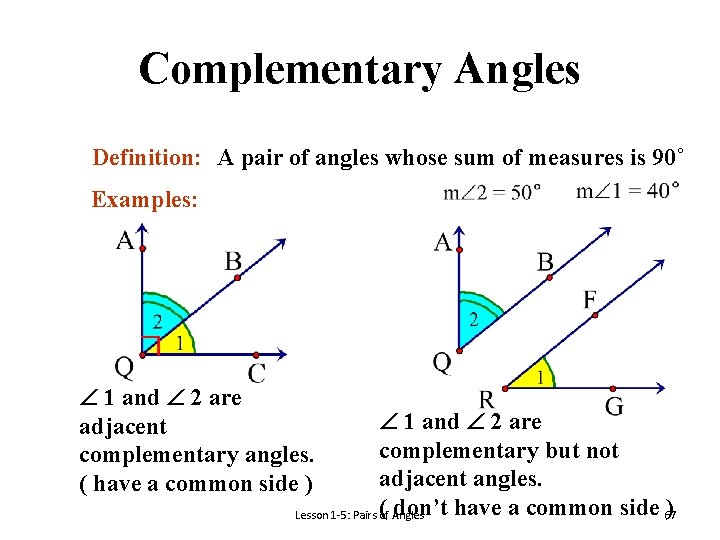
Complementary Angles Definition: A pair of angles whose sum of measures is 90˚ Examples: 1 and 2 are adjacent complementary angles. ( have a common side ) 1 and 2 are complementary but not adjacent angles. ( Angles don’t have a common side 67) Lesson 1 -5: Pairs of

Supplementary Angles Definition: A pair of angles whose sum of measures is 180˚ Examples: 1 and 2 are adjacent supplementary angles. 1 and 2 are supplementary but not adjacent angles. Lesson 1 -5: Pairs of Angles 68

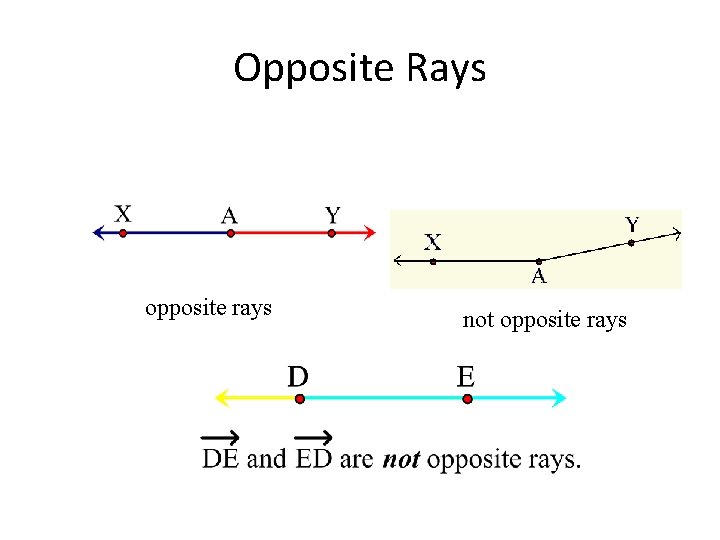
Opposite Rays opposite rays not opposite rays

Opposite Rays Definition: Two rays with the same endpoint, that together form a line. Or (better): Two rays with the same endpoint that together form a straight angle. AX and AY are opposite rays. XAY is a straight angle

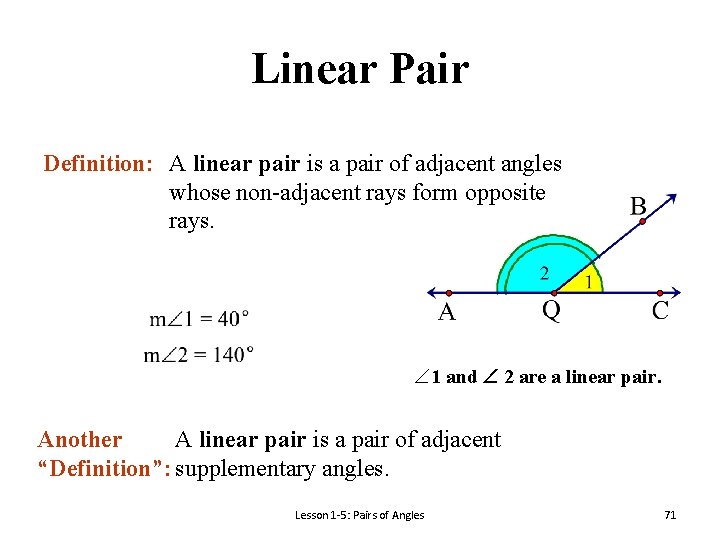
Linear Pair Definition: A linear pair is a pair of adjacent angles whose non-adjacent rays form opposite rays. 1 and 2 are a linear pair. Another A linear pair is a pair of adjacent “Definition”: supplementary angles. Lesson 1 -5: Pairs of Angles 71

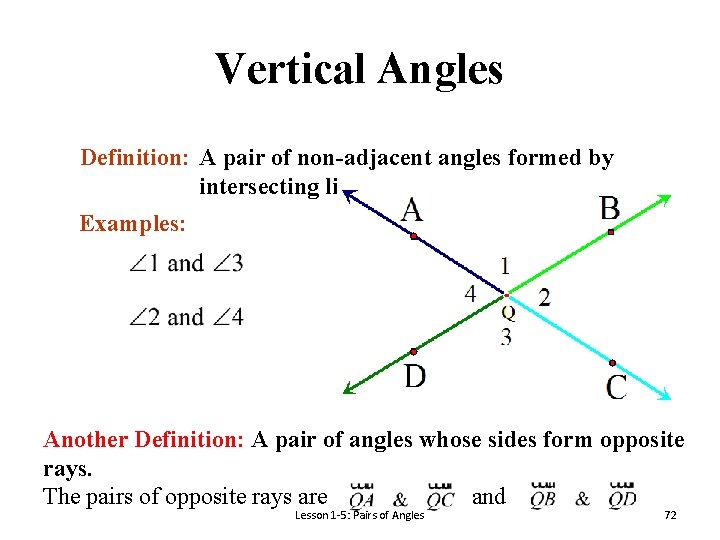
Vertical Angles Definition: A pair of non-adjacent angles formed by intersecting lines. Examples: Another Definition: A pair of angles whose sides form opposite rays. The pairs of opposite rays are and Lesson 1 -5: Pairs of Angles 72

Postulates vs. Theorems Definition: A postulate is a statement we accept as true without proof. Examples: Segment Addition Postulate and Angle Addition Postulate Definition: A theorem is a statement we use logic to show is true. Examples: Linear Pair Theorem and Vertical Angles Theorem (next slides)

Theorem (Linear Pairs) A linear pair is supplementary. Given: Prove: 1 and 2 are a linear pair. 1 and 2 are supplementary. Statements Reasons 1. 1 & 2 are linear pair. 2. and are opposite rays. 3. AQC is a straight angle. 4. m AQC = 180 5. m 1 + m 2 = m AQC 6. m 1 + m 2 = 180 7. 1 and 2 are supplementary. 1. Given 2. Defn. linear pair 3. Defn. opposite rays 4. Defn. straight angle 5. Angle Addition Postulate 6. Substitution Property 7. Defn. supplementary Lesson 1 -5: Pairs of Angles

Vertical Angles Theorem Vertical angles are congruent. Lesson 1 -5: Pairs of Angles 75

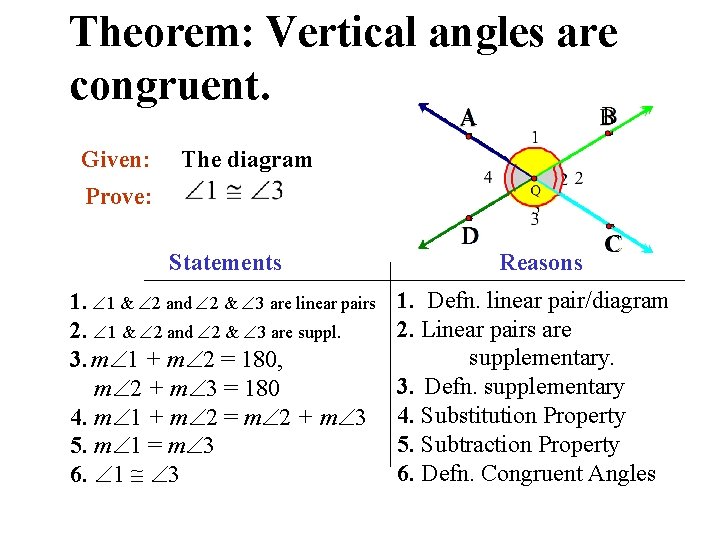
Theorem: Vertical angles are congruent. Given: The diagram Prove: Statements 1. 1 & 2 and 2 & 3 are linear pairs 2. 1 & 2 and 2 & 3 are suppl. 3. m 1 + m 2 = 180, m 2 + m 3 = 180 4. m 1 + m 2 = m 2 + m 3 5. m 1 = m 3 6. 1 3 Reasons 1. Defn. linear pair/diagram 2. Linear pairs are supplementary. 3. Defn. supplementary 4. Substitution Property 5. Subtraction Property 6. Defn. Congruent Angles

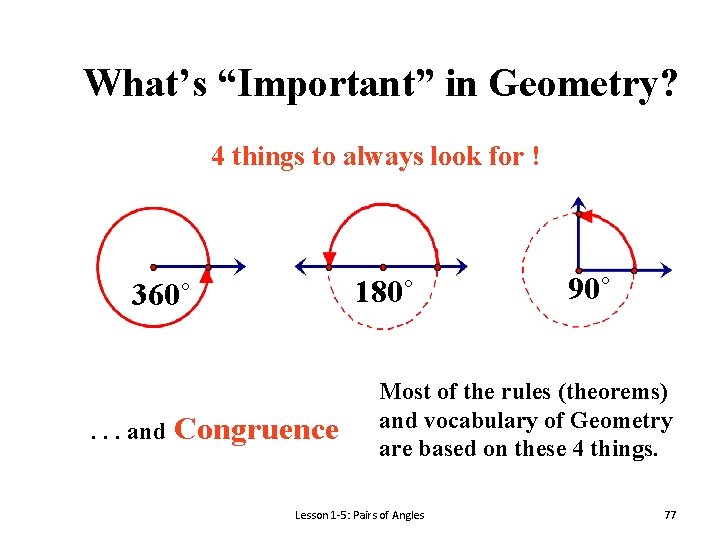
What’s “Important” in Geometry? 4 things to always look for ! 180˚ 360˚ . . . and Congruence 90˚ Most of the rules (theorems) and vocabulary of Geometry are based on these 4 things. Lesson 1 -5: Pairs of Angles 77

Algebra and Geometry Common Algebraic Equations used in Geometry: ( ( )+( )+( )=( ) ) = 90˚ ) = 180˚ If the problem you’re working on has a variable (x), then consider using one of these equations. Lesson 1 -5: Pairs of Angles 78

Example: If m 4 = 67º, find the measures of all other angles. Step 1: Mark the figure with given info. Step 2: Write an equation. 67º Lesson 1 -5: Pairs of Angles 79

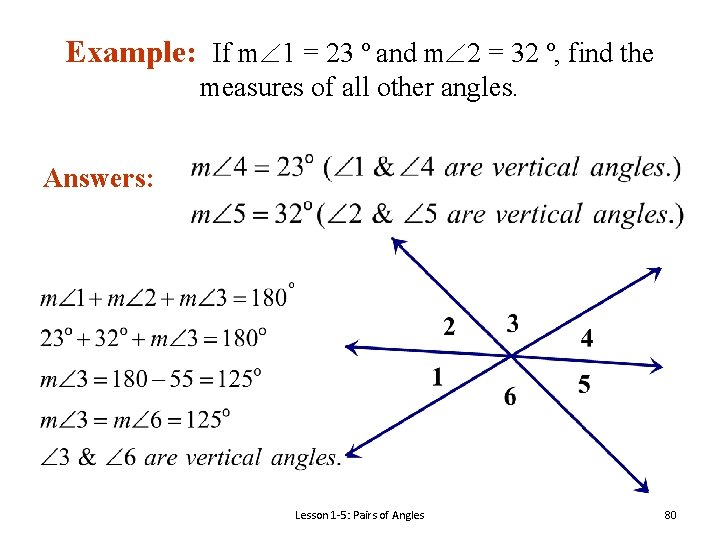
Example: If m 1 = 23 º and m 2 = 32 º, find the measures of all other angles. Answers: Lesson 1 -5: Pairs of Angles 80

Example: If m 1 = 44º, m 7 = 65º find the measures of all other angles. Answers: Lesson 1 -5: Pairs of Angles 81