INTRODUCTION TO LINEAR PROGRAMMING CONTENTS l Introduction to





























- Slides: 42

INTRODUCTION TO LINEAR PROGRAMMING CONTENTS l Introduction to Linear Programming l Applications of Linear Programming Reference: Chapter 1 in BJS book. 1

Linear Programming Problem l Features of Linear programming problem: u Decision Variables u We maximize (or minimize) a linear function of decision variables, called objective function. u The decision variables must satisfy a set of constraints. u Decision variables have sign restrictions. l Example: Maximize z subject to 2 x 1 + x 2 x 1 , x 2 0 = 3 x 1 + 2 x 2 100 80 40 2

A Typical Linear Programming Problem Linear Programming Formulation: Minimize c 1 x 1 + c 2 x 2 + c 3 x 3 + …. + cnxn Linear Objective subject to a 11 x 1 + a 12 x 2 + a 13 x 3 + …. + a 1 nxn b 1 a 21 x 1 + a 22 x 2 + a 23 x 3 + …. + a 2 nxn b 2 : : am 1 x 1 + am 2 x 2 + am 3 x 3 + …. + amnxn bm x 1, x 2, x 3 , …. , xn 0 or, Minimize subject to Linear Constraints; - Technology - Uncontrolable variables/factors Decision (controlable) variables - Can take any real value - Restricted or unrestrited in sign j=1, n cjxj j=1, n aijxj - xn+i = bi for all i = 1, …, m xj 0 for all j =1, …, n+m 3 Standard form representation

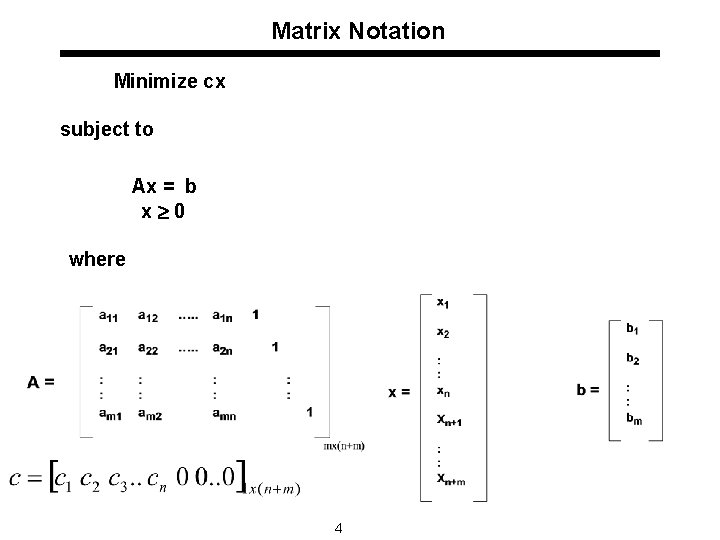
Matrix Notation Minimize cx subject to Ax = b x 0 where 4

Linear Programming Modeling and Examples l Stages of an application: u Problem formulation u Mathematical model u Deriving a solution u Model testing and analysis u Implementation 5

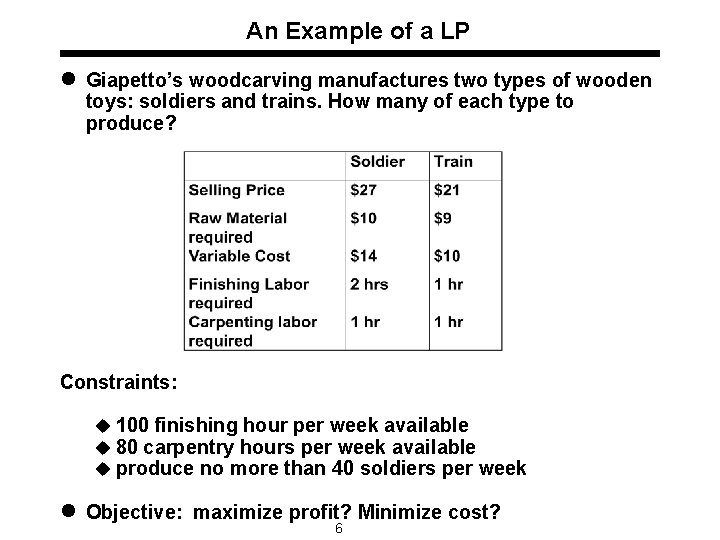
An Example of a LP l Giapetto’s woodcarving manufactures two types of wooden toys: soldiers and trains. How many of each type to produce? Constraints: u 100 finishing hour per week available u 80 carpentry hours per week available u produce no more than 40 soldiers per week l Objective: maximize profit? Minimize cost? 6

An Example of a LP (cont. ) Linear Programming formulation: Maximize z = 3 x 1 + 2 x 2 (Obj. Func. ) subject to 2 x 1 + x 1 x 2 100 x 2 80 40 0 x 2 0 (Finishing constraint) (Carpentry constraint) (Bound on soldiers) (Sign restriction) 7

Assumptions of Linear Programming l Proportionality Assumption u Contribution of a variable is proportional to its value. l Additivity Assumptions u Contributions of variables are independent. l Divisibility Assumption u Decision variables can take fractional values. l Certainty Assumption u Each parameter is known with certainty. 8

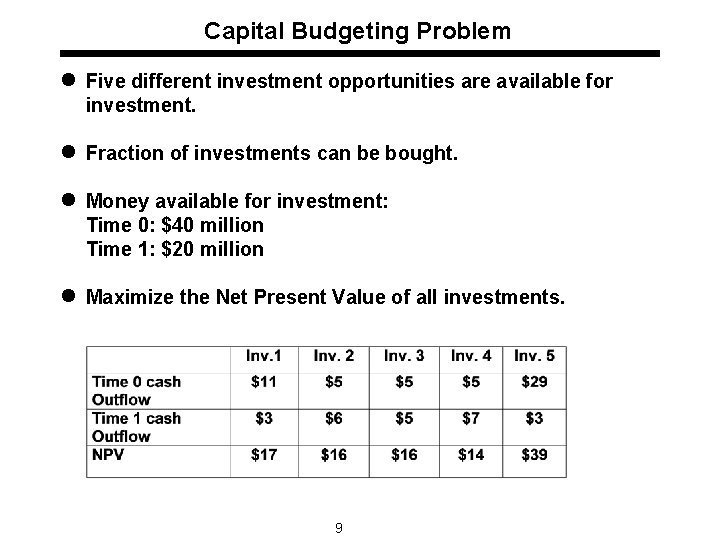
Capital Budgeting Problem l Five different investment opportunities are available for investment. l Fraction of investments can be bought. l Money available for investment: Time 0: $40 million Time 1: $20 million l Maximize the Net Present Value of all investments. 9

Transportation Problem l The Brazilian coffee company processes coffee beans into coffee at m plants. The production capacity at plant i is ai. l The coffee is shipped every week to n warehouses in major cities for retail, distribution, and exporting. The demand at warehouse j is bj. l The unit shipping cost from plant i to warehouse j is cij. l It is desired to find the production-shipping pattern xij from plant i to warehouse j, i = 1, . . , m, j = 1, …, n, that minimizes the overall shipping cost. l What is Xij? Produced? Shipped? l Why not consider production and shipping together? l Why not maximize profit? 10

Static Workforce Scheduling l Number of full time employees on different days of the week are given below. l Each employee must work five consecutive days and then receive two days off. l The schedule must meet the requirements by minimizing the total number of full time employees. l Decision variable? 11

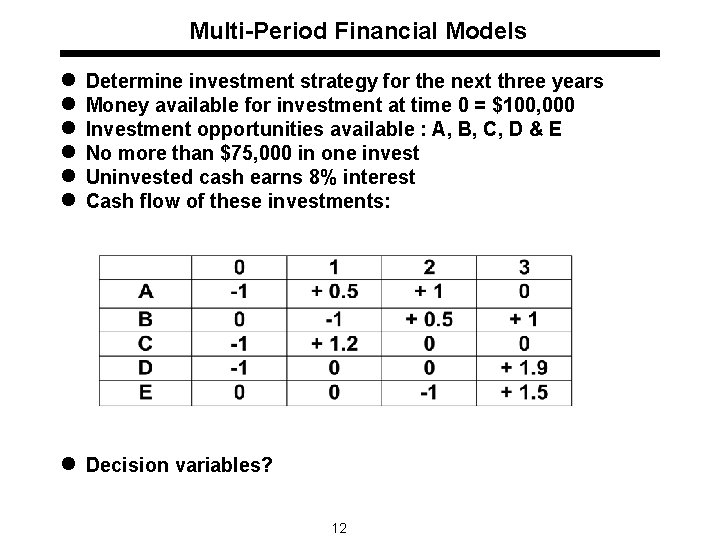
Multi-Period Financial Models l l l Determine investment strategy for the next three years Money available for investment at time 0 = $100, 000 Investment opportunities available : A, B, C, D & E No more than $75, 000 in one invest Uninvested cash earns 8% interest Cash flow of these investments: l Decision variables? 12

Cutting Stock Problem l A manufacturer of metal sheets produces rolls of standard fixed width w and of standard length l. l A large order is placed by a customer who needs sheets of width w and varying lengths. He needs bi sheets of length li, i = 1, …, m. l The manufacturer would like to cut standard rolls in such a way as to satisfy the order and to minimize the waste. l Since scrap pieces are useless to the manufacturer, the objective is to minimize the number of rolls needed to satisfy the order. 13

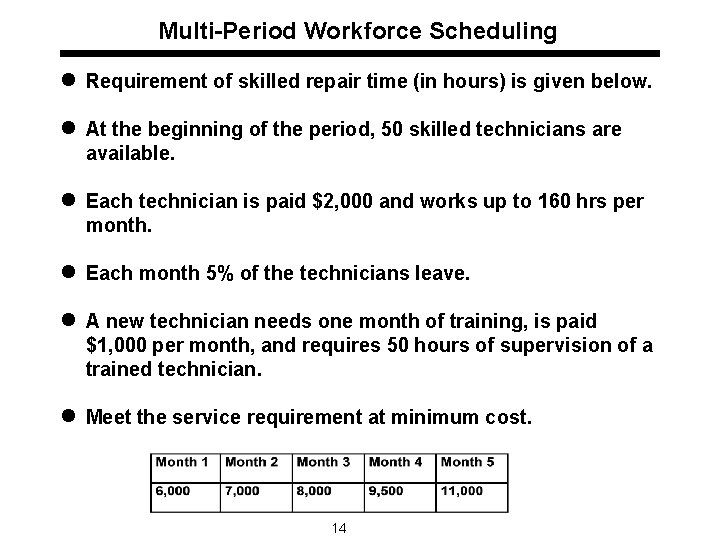
Multi-Period Workforce Scheduling l Requirement of skilled repair time (in hours) is given below. l At the beginning of the period, 50 skilled technicians are available. l Each technician is paid $2, 000 and works up to 160 hrs per month. l Each month 5% of the technicians leave. l A new technician needs one month of training, is paid $1, 000 per month, and requires 50 hours of supervision of a trained technician. l Meet the service requirement at minimum cost. 14

Solution: Capital Budgeting Problem Decision Variables: xi: fraction of investment i purchased Formulation: Maximize z = 17 x 1 + 16 x 2 + 16 x 3 + 14 x 4 + 39 x 5 subject to 40 20 1 1 x 5 1 x 1, x 2, x 3, x 4, x 5 0 11 x 1 + 53 x 2 + 5 x 3 + 5 x 4 + 29 x 5 3 x 1 + 6 x 2 + 5 x 3 + x 4 + 34 x 5 x 1 x 2 x 3 x 4 15

Solution: Transportation Problem Decision Variables: xij: amount shipped from plant i to warehouse j Formulation: Minimize z = subject to = ai, i = 1, … , m bj, j = 1, … , n xij 0, i = 1, … , m, j = 1, … , n 16

Solution: Static Workforce Scheduling LP Formulation: Min. z = x 1+ x 2 + x 3 + x 4 + x 5 + x 6 + x 7 subject to x 1 + x 4 + x 5 + x 6 + x 7 x 1 + x 2 + x 3 + x 4 + x 5 x 2 + x 3 + x 4 + x 5 + x 6 + x 7 x 1 , x 2 , x 3 , x 4 , x 5 , x 6 , x 7 0 17 17 13 15 19 14 16 11

Solution: Multi period Financial Model Decision Variables: A, B, C, D, E : Dollars invested in the investments A, B, C, D, and E St: Dollars invested in money market fund at time t (t = 0, 1, 2) Formulation: Maximize z = B + 1. 9 D + 1. 5 E + 1. 08 S 2 subject to A + C + D + S 0 = 100, 000 0. 5 A + 1. 2 C + 1. 08 S 0 = B + S 1 A + 0. 5 B + 1. 08 S 1 = E + S 2 A 75, 000 B 75, 000 C 75, 000 D 75, 000 E 75, 000 A, B, C, D, E, S 0, S 1, S 2 0 18

Solution: Multiperiod Workforce Scheduling Decision Variables: xt: number of technicians trained in period t yt: number of experienced technicians in period t Formulation: Minimize z = 1000(x 1 + x 2 + x 3 + x 4 + x 5) + 2000(y 1 + y 2 + y 3 + y 4 + y 5) subject to 160 y 1 - 50 x 1 160 y 2 - 50 x 2 160 y 3 - 50 x 3 160 y 4 - 50 x 4 160 y 5 - 50 x 5 6000 7000 8000 9500 11000 y 1 = 50 0. 95 y 1 + x 1 = y 2 0. 95 y 2 + x 2 = y 3 0. 95 y 3 + x 3 = y 4 0. 95 y 4 + x 4 = y 5 xt, yt 0, t = 1, 2, 3, … , 5 19

Cutting Stock Problem (contd. ) l Given a standard sheet of length l, there are many ways of cutting it. Each such way is called a cutting pattern. l The jth cutting pattern is characterized by the column vector aj, where the ith component, namely, aij, is a nonnegative integer denoting the number of sheets of length li in the jth pattern. l Note that the vector aj represents a cutting pattern if and only if i=1, n aijli l and each aij is a nonnegative number. 20

Cutting Stock Problem (contd. ) Formulation: xi: Number of sheets cut using patter j Minimize i=1, n xi subject to i=1, n aij xi bi i = 1, …, m xi 0 j = 1, …, n xi integer j = 1, …, n 21

Cutting Stock Problem (contd. ) Formulation: Let l = 7, and type 1, type 2 and type 3 sizes demanded are 2, 3, and 5 with b 1=10, b 2=4, b 4=3. possible patterns: i j 3 0 0 2 1 0 0 2 0 Min. z = x 1+ x 2 + x 3 + x 4 subject to 3 x 1+2 x 2 + x 4 10 x 2 + 2 x 3 4 x 4 3 xj integer j = 1, …, 4 22 1 0 1

Modeling issues l Mini- max objective (scenario based modeling): => Minimizing the maximum regret in decision making under uncertain outcomes fi(x) is the cost of the outcome under scenario i (equally likely scenarios) fi(x)=return of best decision under scenario i – return of the decision as a solution of the model above 23

Modeling issues l Max-Min objective: => 24

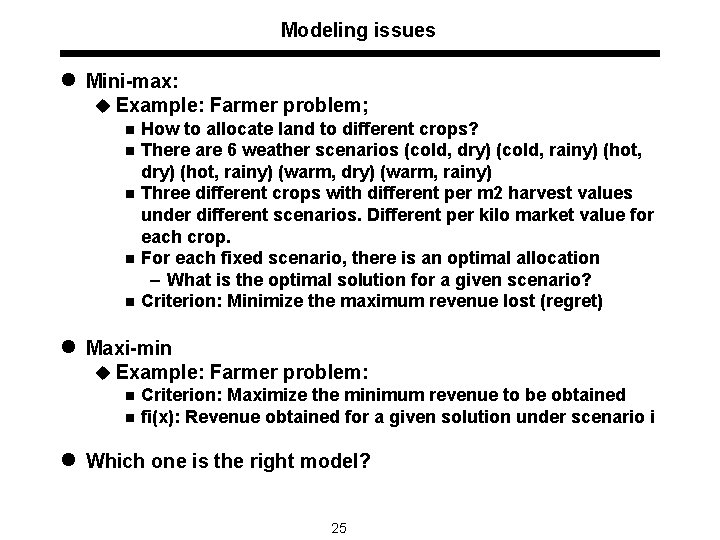
Modeling issues l Mini-max: u Example: Farmer problem; n How to allocate land to different crops? n There are 6 weather scenarios (cold, dry) (cold, rainy) (hot, dry) (hot, rainy) (warm, dry) (warm, rainy) n Three different crops with different per m 2 harvest values under different scenarios. Different per kilo market value for each crop. n For each fixed scenario, there is an optimal allocation – What is the optimal solution for a given scenario? n Criterion: Minimize the maximum revenue lost (regret) l Maxi-min u Example: Farmer problem: n Criterion: Maximize the minimum revenue to be obtained n fi(x): Revenue obtained for a given solution under scenario i l Which one is the right model? 25

Modeling issues l Minimize/Maximize absolute value => For maximimization problems multiply objective with -1 and turn them into minimization problem 26

Modeling issues 27

Modeling issues l Is the absolute value a linear function? u A function is a linear function if it satisfies the following two conditons; n n f(a+b)=f(a)+f(b) f(ax)= af(x) (for any real “a” value) l For the absolute function, we can find a counter example easily; u Let f(x)=|x| u f(-1+3) = |-1+3|=2 but f(-1)+f(3) = 1+3 = 4 first condition is violated. Therefore absolute value is not a linear function (proof by contradiction) 28

Modeling issues l Fixed charge problem: Cost function with a fixed part 29

Modeling issues l Either-or constraints: l 1 out of k type constraints 30

Modeling issues l If-then constraints 31

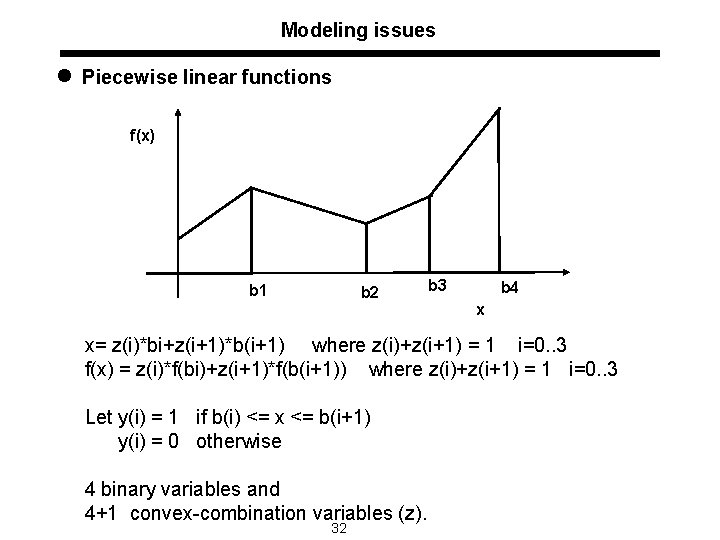
Modeling issues l Piecewise linear functions f(x) b 1 b 2 b 3 b 4 x x= z(i)*bi+z(i+1)*b(i+1) where z(i)+z(i+1) = 1 i=0. . 3 f(x) = z(i)*f(bi)+z(i+1)*f(b(i+1)) where z(i)+z(i+1) = 1 i=0. . 3 Let y(i) = 1 if b(i) <= x <= b(i+1) y(i) = 0 otherwise 4 binary variables and 4+1 convex-combination variables (z). 32

Modeling issues Piecewise linear functions 33

Modeling issues Piecewise linear functions; Alternative formulation This model is not correct 34

Examples for some modelling constructs l Consider the transportation model u Either or; Either we transfer from facility 3 to 4 or from 3 to 5, not both simultaneously. u If then; If we transfer from facility 3 to 4, we must not transfer from facility 3 to 5 (If X 34>0 then X 35<=0 (-X 35>=0)) 35

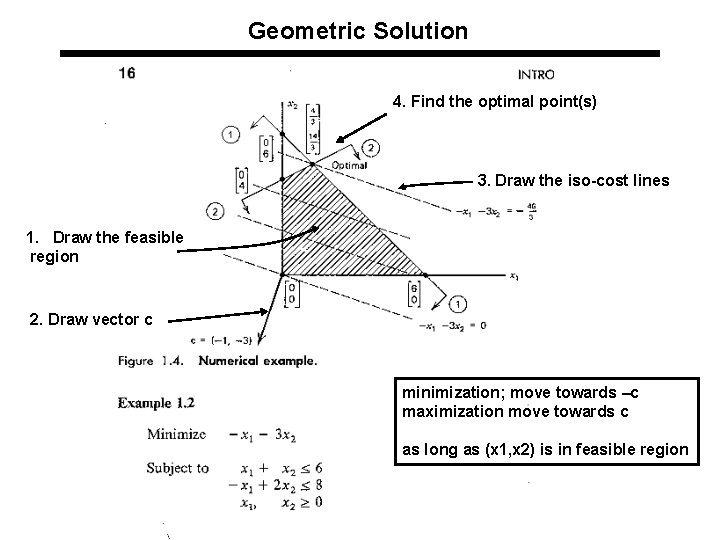
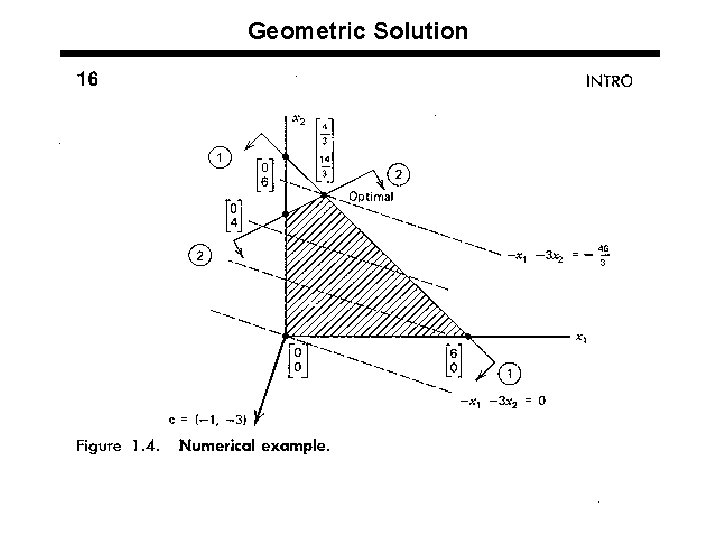
Geometric Solution l Steps of the geometric solution u Determine and draw the feasible region u Draw the c vector u Draw the iso cost lines (perpendicular to c vector) u Find the last point(s) that iso-cost lines touch the feasible region, when we move towards direction of –c (in minimization). This point (or points) is the optimal solution. 36

Geometric Solution 4. Find the optimal point(s) 3. Draw the iso-cost lines 1. Draw the feasible region 2. Draw vector c minimization; move towards –c maximization move towards c as long as (x 1, x 2) is in feasible region 37

Geometric Solution 38

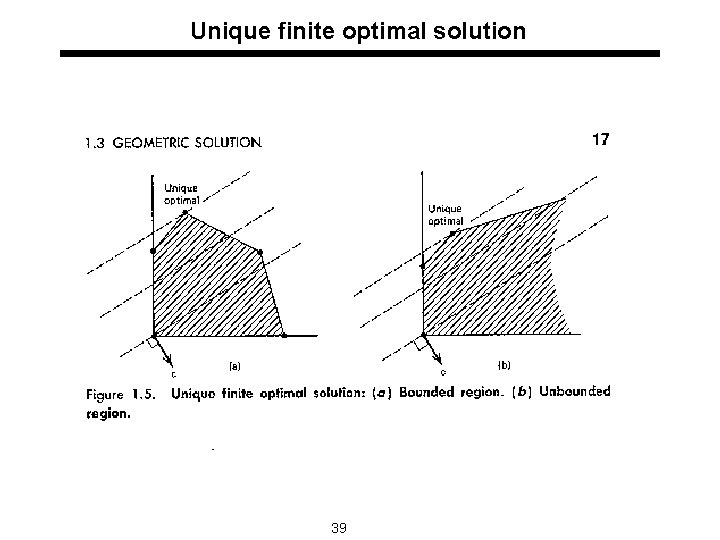
Unique finite optimal solution 39

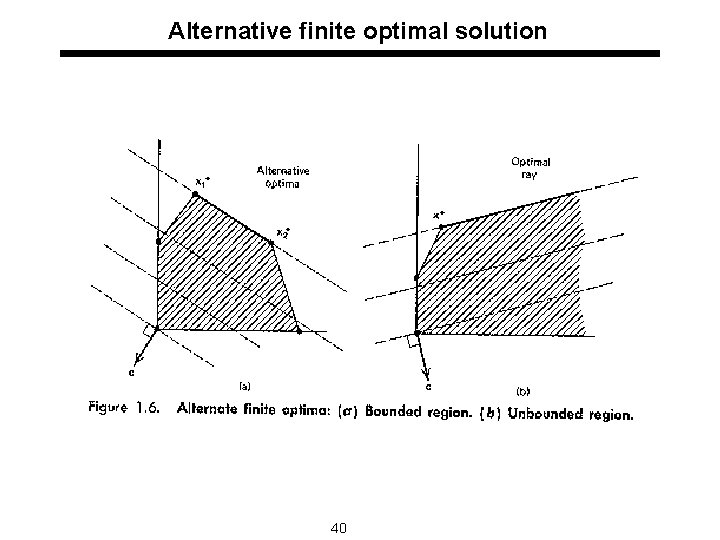
Alternative finite optimal solution 40

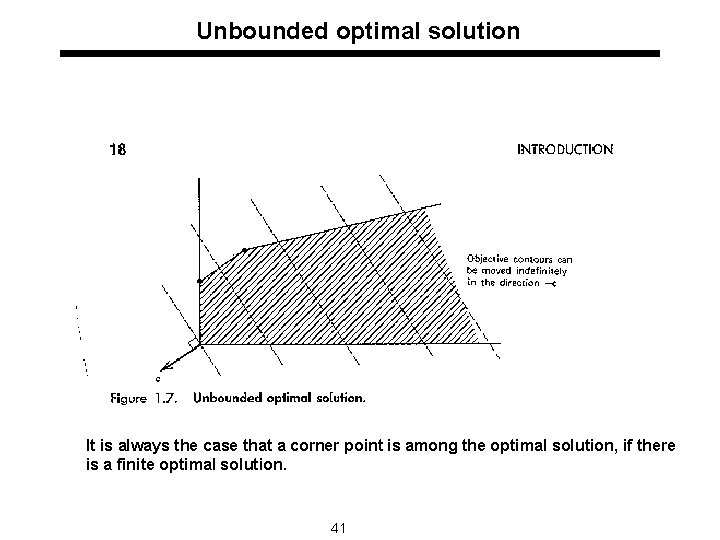
Unbounded optimal solution It is always the case that a corner point is among the optimal solution, if there is a finite optimal solution. 41

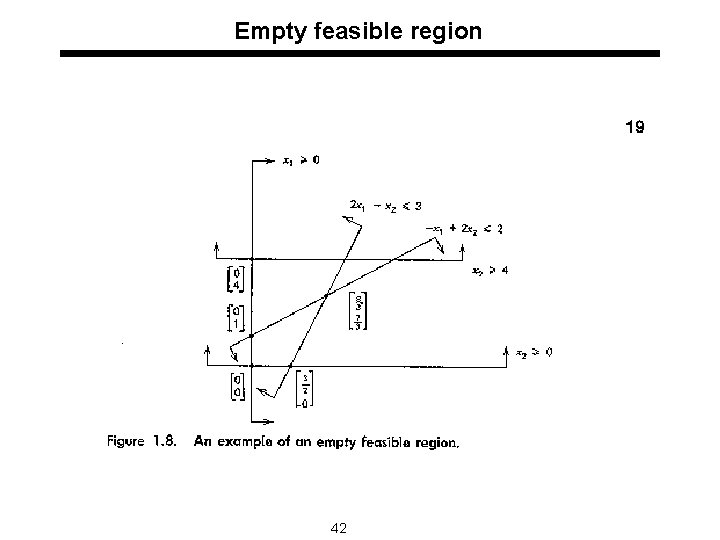
Empty feasible region 42
 Perbedaan linear programming dan integer programming
Perbedaan linear programming dan integer programming Linear vs integer programming
Linear vs integer programming Programing adalah
Programing adalah Contents introduction
Contents introduction Greedy algorithm vs dynamic programming
Greedy algorithm vs dynamic programming What is system programing
What is system programing Simplex method example problems with solutions
Simplex method example problems with solutions Difference constraints and shortest paths
Difference constraints and shortest paths Canonical form of linear programming problem
Canonical form of linear programming problem Linear programming case study examples
Linear programming case study examples Non negativity constraints
Non negativity constraints Scope of linear programming
Scope of linear programming Network model linear programming
Network model linear programming What is linear programming in management science
What is linear programming in management science Linear management
Linear management Linear programming word problems
Linear programming word problems Characteristics of
Characteristics of Formulation of lpp examples
Formulation of lpp examples Pengertian linear programming
Pengertian linear programming Lp model formulation
Lp model formulation Linear vs integer programming
Linear vs integer programming Scope of linear programming
Scope of linear programming Linear goal programming
Linear goal programming Linear programming powerpoint
Linear programming powerpoint The zj row in a simplex table for maximization represents
The zj row in a simplex table for maximization represents Operations management linear programming
Operations management linear programming What is linear programming in management science
What is linear programming in management science Linear programming graphical calculator
Linear programming graphical calculator Role of sensitivity analysis in linear programming
Role of sensitivity analysis in linear programming Linear programming in operation research
Linear programming in operation research 3-3 optimization with linear programming
3-3 optimization with linear programming Saba neyshabouri
Saba neyshabouri Linear programming relaxation
Linear programming relaxation Qm for windows
Qm for windows Operations management linear programming
Operations management linear programming Linear programming definition
Linear programming definition Assignment problem hungarian method
Assignment problem hungarian method Linear programming: simplex method
Linear programming: simplex method 3-4 linear programming
3-4 linear programming Solving linear programming problems graphically
Solving linear programming problems graphically Unbounded solution simplex method
Unbounded solution simplex method Linear programming
Linear programming Algebra 2 linear programming
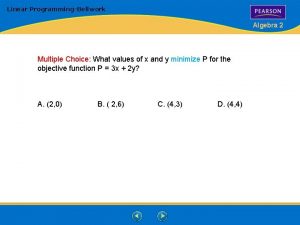
Algebra 2 linear programming