Management Science MNG 221 Linear Programming Graphical Solution

Management Science – MNG 221 Linear Programming: Graphical Solution

Linear Programming: Introduction • Most Firms Objectives - Maximize profit (Overall Org. ) - Minimize cost (Individual Depts. ) • Constraints/Restrictions - Limited Resources, - Restrictive Guidelines • Linear Programming is a model that consists of linear relationships representing a firm’s decision(s), given an objective and resource constraints.

Linear Programming: Introduction • Steps in applying the linear programming technique 1. Problem must be solvable by linear programming 2. The unstructured problem must be formulated as a mathematical model. 3. Problem must be solved using established mathematical techniques.

Linear Programming: Introduction • The linear programming technique derives its name from the fact that: 1. the functional relationships in the mathematical model are linear (Capable of being represented by a straight line), 2. and the solution technique consists of predetermined mathematical steps that is, a Program (a system of procedures or activities that has a specific purpose).

Linear Programming: Model Formulation A linear programming model consists of: • Objective function: reflects the objective of the firm in terms of the decision variables Always consists of: • Maximizing profit • Minimizing cost

Linear Programming: Model Formulation • Constraints: a restriction on decision making placed on the firm by the operating environment • E. g. Raw materials, labour, market size etc. • The Objective Function and Constraints consists of: • Decision variables: mathematical symbols that represent levels of activity e. g. x 1, x 2, x 3 etc. • Parameters: numerical values that are included in the objective functions and constraints E. g. 40 hrs

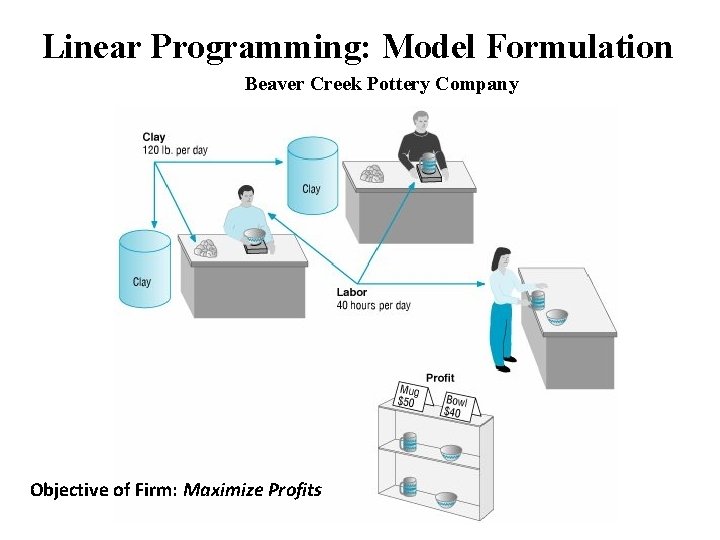
Linear Programming: Model Formulation Beaver Creek Pottery Company Objective of Firm: Maximize Profits

Linear Programming: Maximization Problem Model Formulation Step 1: Define the decision variables Øx 1 – number of bowls Øx 2 – number of mugs Step 2: Define the objective function Maximize profit Step 3: Define the constraints ØClay - A total 120 Lbs ØLabour – A total 40 hrs

Linear Programming: Maximization Problem Resource Requirements Product Labour Clay Profit (Hr/Unit) (Lb/Unit) $/Unit Bowl 1 4 40 Mug 2 3 50 There are 40 labour hours and 120 pounds of clay available Step 1: Define the decision variables x 1 – number of bowls x 2 – number of mugs Step 2: Define the objective function Z = 40 x 1 + 50 x 2 Step 3: Define the constraints x 1 + 2 x 2 ≤ 40 4 x 1 + 3 x 2 ≤ 120 Non-negativity constraints x 1, x 2 ≥ 0 Step 4: Solve the problem

Linear Programming: Maximization Problem • The complete linear programming model for this problem can now be summarized as follows: Maximize Z = 40 x 1 + 50 x 2 Where x 1 + 2 x 2 ≤ 40 4 x 1 + 3 x 2 ≤ 120 x 1, x 2 ≥ 0

Linear Programming: Maximization Problem The solution of this model will result in numeric values for x 1 and x 2 that will maximize total profit, Z, but should not be infeasible • A feasible solution does not violate any of the constraints. E. g. x 1= 5, x 2= 10 • An infeasible problem violates at least one of the constraints. E. g. x 1= 10, x 2= 20

Linear Programming: Graphical Solution • The next stage in the application of linear programming is to find the solution of the model • A common solution approach is to solve algebraically: v. Manually v. Computer Program

Linear Programming: Graphical Solution • Graphical Solutions are limited to linear programming problems with only two decision variables. • The graphical method provides a picture of how a solution is obtained for a linear programming problem

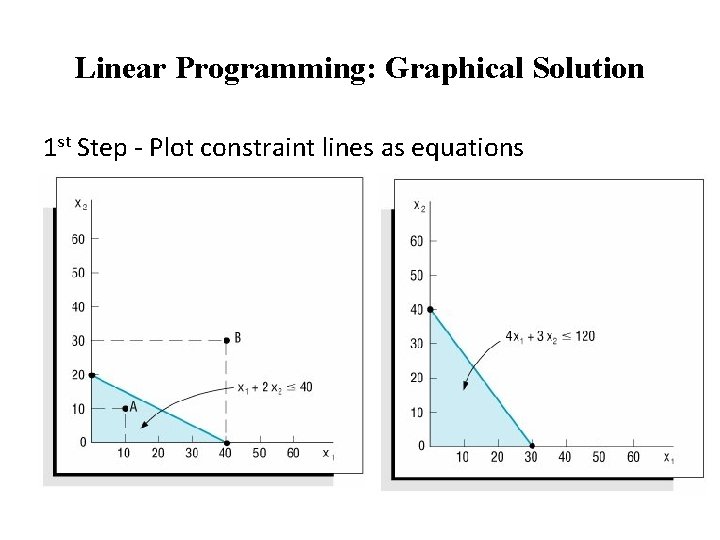
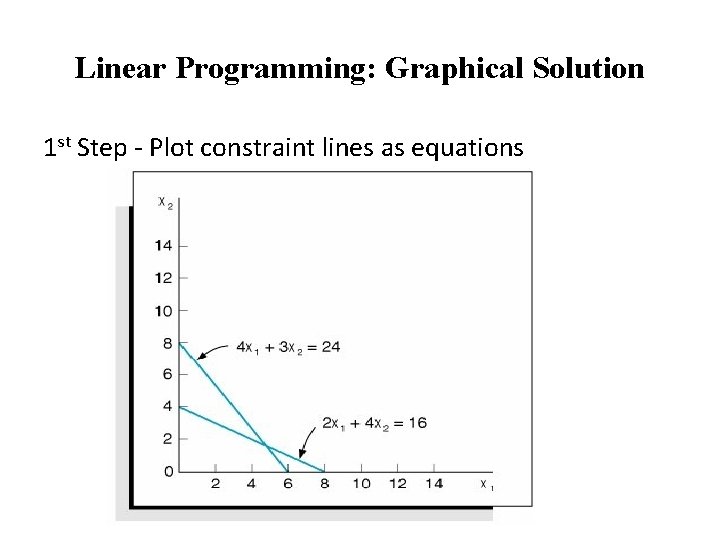
Linear Programming: Graphical Solution 1 st Step - Plot constraint lines as equations

Linear Programming: Graphical Solution Plotting Line • Determine two points that are on the line and then draw a straight line through the points. • One point can be found by letting x 1 = 0 and solving for x 2: • A second point can be found by letting x 2 = 0 and solving for x 1:

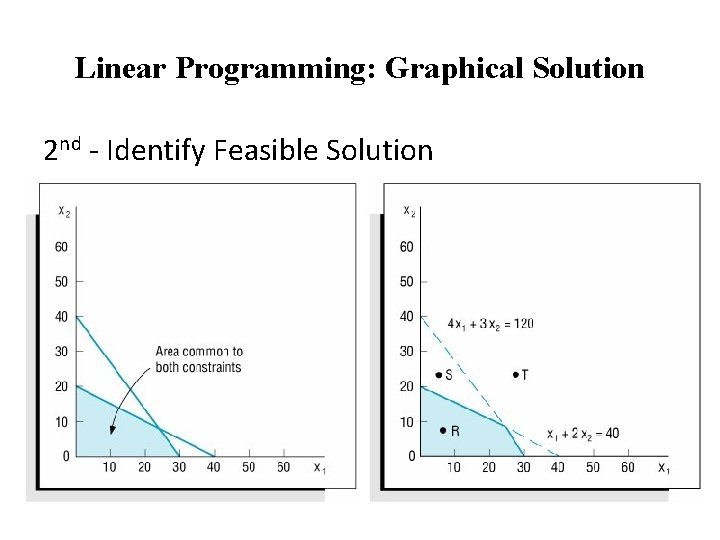
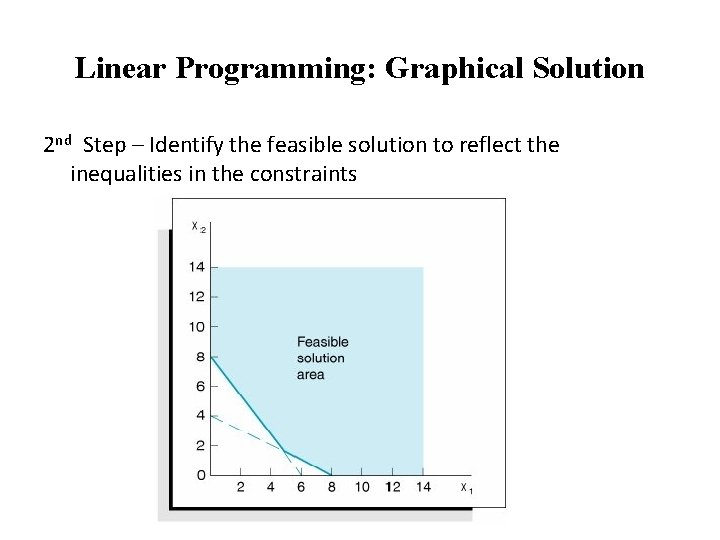
Linear Programming: Graphical Solution 2 nd - Identify Feasible Solution

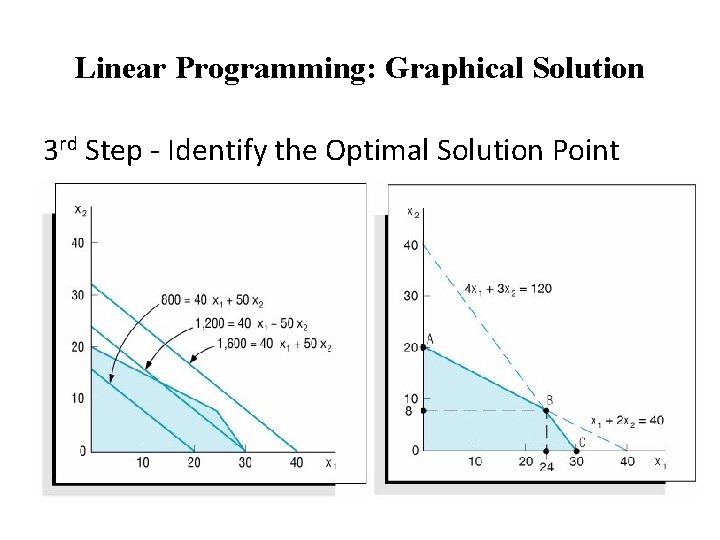
Linear Programming: Graphical Solution 3 rd Step - Identify the Optimal Solution Point

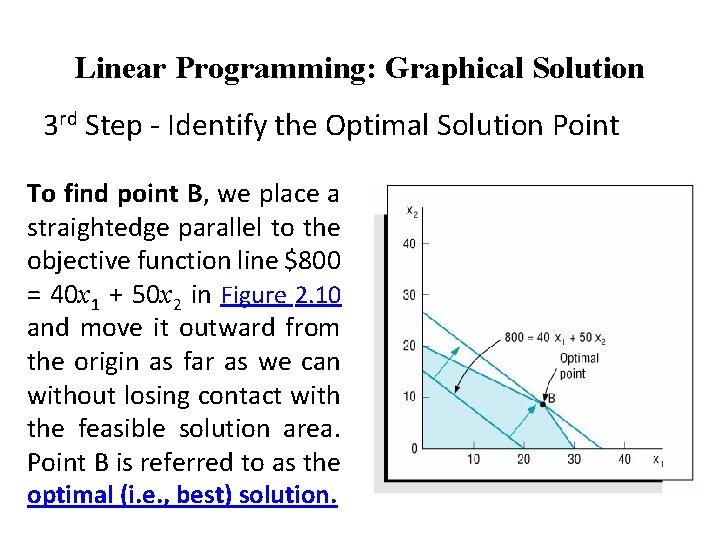
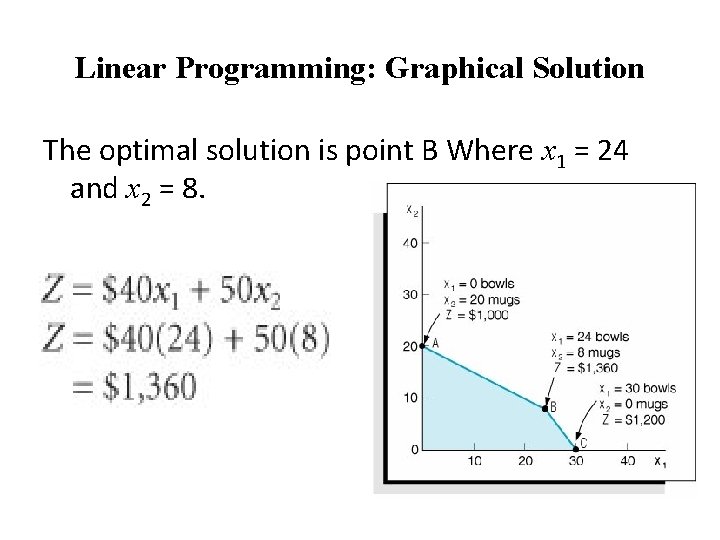
Linear Programming: Graphical Solution 3 rd Step - Identify the Optimal Solution Point To find point B, we place a straightedge parallel to the objective function line $800 = 40 x 1 + 50 x 2 in Figure 2. 10 and move it outward from the origin as far as we can without losing contact with the feasible solution area. Point B is referred to as the optimal (i. e. , best) solution.

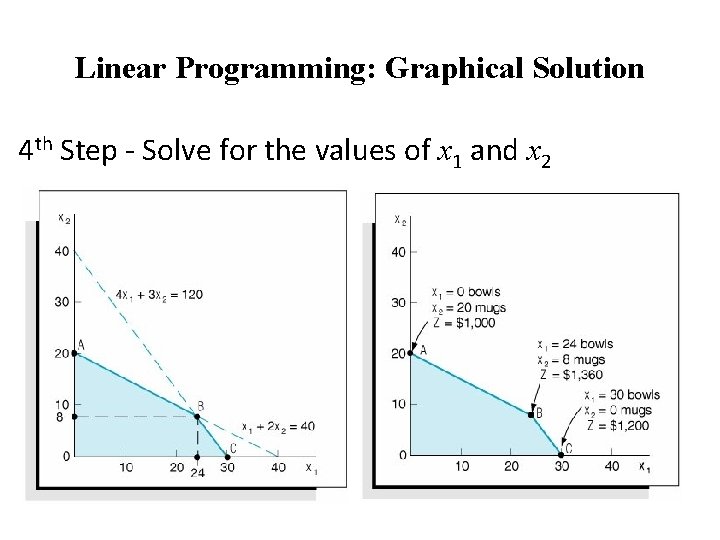
Linear Programming: Graphical Solution 4 th Step - Solve for the values of x 1 and x 2

Linear Programming: Graphical Solution • The Optimal Solution Point is the last point the objective function touches as it leaves the feasible solution area. • Extreme Points are corner points on the boundary of the feasible solution area. E. g. A, B or C

Linear Programming: Graphical Solution • Constraint Equations are solved simultaneously at the optimal extreme point to determine the variable solution values. v. First, convert both equations to functions of x 1: v. Now let x 1 in the 1 st eq. equal x 1 in the 2 nd eq. 40 - 2 x 2 = 30 - (3 x 2/4)

Linear Programming: Graphical Solution v And solve for x 2: v. Substituting x 2 = 8 in one the original equations:

Linear Programming: Graphical Solution The optimal solution is point B Where x 1 = 24 and x 2 = 8.

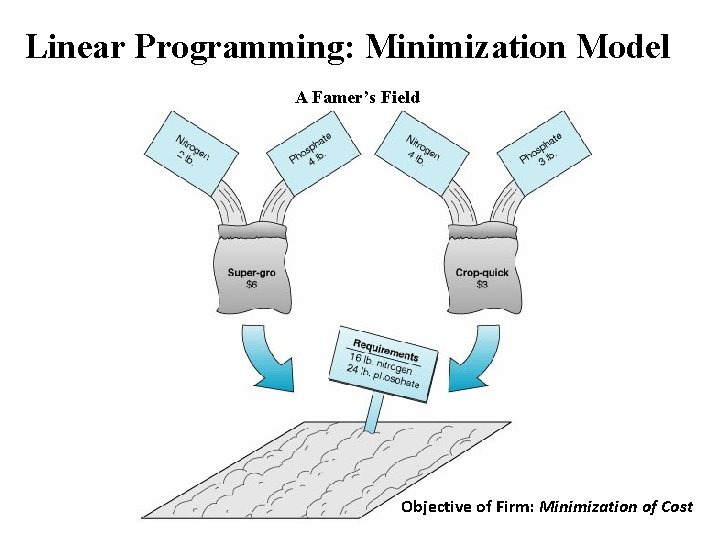
Linear Programming: Minimization Model A Famer’s Field Objective of Firm: Minimization of Cost

Linear Programming: Graphical Solution • A farmer is preparing to plant a crop in the spring and needs to fertilize a field. There are two brands of fertilizer to choose from, Super-gro and Crop-quick. Each brand yields a specific amount of nitrogen and phosphate per bag, as follows: Chemical Contribution Brand NITROGEN PHOSPHATE (LB. /BAG) Super-gro 2 4 Crop-quick 4 3

Linear Programming: Graphical Solution • The farmer's field requires at least v 16 pounds of nitrogen and v 24 pounds of phosphate. • Super-gro costs $6 per bag, and • Crop-quick costs $3. • The farmer wants to know how many bags of each brand to purchase in order to minimize the total cost of fertilizing.

Linear Programming: Minimization Problem Model Formulation Step 1: Define the Decision Variables v. How many bags of Super-gro and Crop-quick to buy Step 2: Define the Objective Function v. Minimize cost Step 3: Define the Constraints v. The field requirements for nitrogen and phosphate

Linear Programming: Minimization Problem Step 1: Define the decision variables x 1 = bags of Super-gro Chemical Contribution Brand NITROGEN (LB. /BAG) PHOSPHATE (LB. /BAG) Super-gro 2 4 Crop-quick 4 3 The field requires at least 16 pounds of nitrogen and 24 pounds of phosphate. x 2 = bags of Crop-quick Step 2: Define the objective function Minimize Z = $6 x 1 + 3 x 2 Step 3: Define the constraints 2 x 1 + 4 x 2 ≥ 16 lb. 4 x 1 + 3 x 2 ≥ 24 lb Minimum Requirement Non-negativity constraints x 1, x 2 ≥ 0 Step 4: Solve the problem

Linear Programming: Maximization Problem • The complete model formulation for this minimization problem is: Minimize Z = $6 x 1 + 3 x 2 Where 2 x 1 + 4 x 2 ≥ 16 lb. 4 x 1 + 3 x 2 ≥ 24 lb x 1, x 2 ≥ 0

Linear Programming: Graphical Solution 1 st Step - Plot constraint lines as equations

Linear Programming: Graphical Solution 2 nd Step – Identify the feasible solution to reflect the inequalities in the constraints

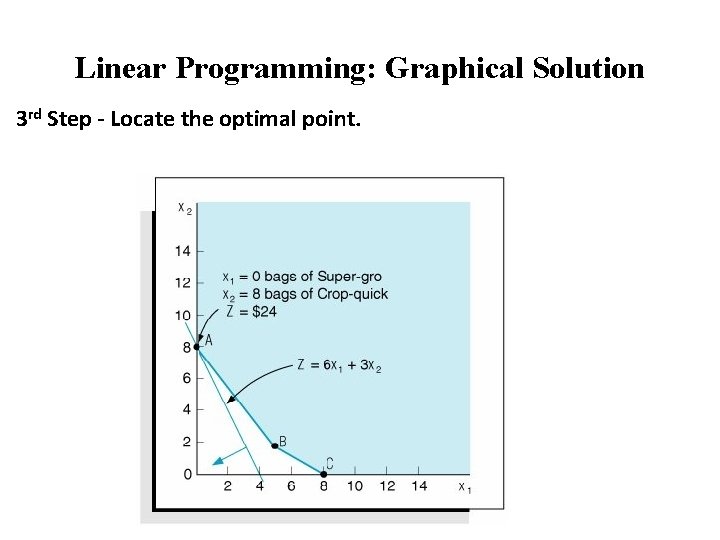
Linear Programming: Graphical Solution 3 rd Step - Locate the optimal point.

Linear Programming: Graphical Solution • The Optimal Solution of a minimization problem is at the extreme point closest to the origin. • Extreme Points are corner points on the boundary of the feasible solution area. E. g. A, B Or C • As the Objective Function edges toward the origin, the last point it touches in the feasible solution area is A. In other words, point A is the closest the objective function can get to the origin without encompassing infeasible points.

Linear Programming: Graphical Solution v And solve for x 2: v. Given that the optimal solution is x 1 = 0, x 2 = 8, the minimum cost, Z, is