Introduction to Inference Tests of Significance Proof 925

































- Slides: 48

Introduction to Inference Tests of Significance

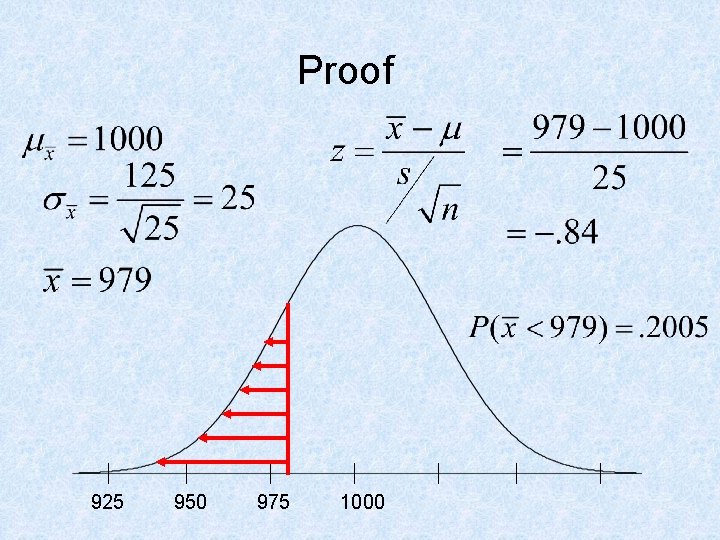
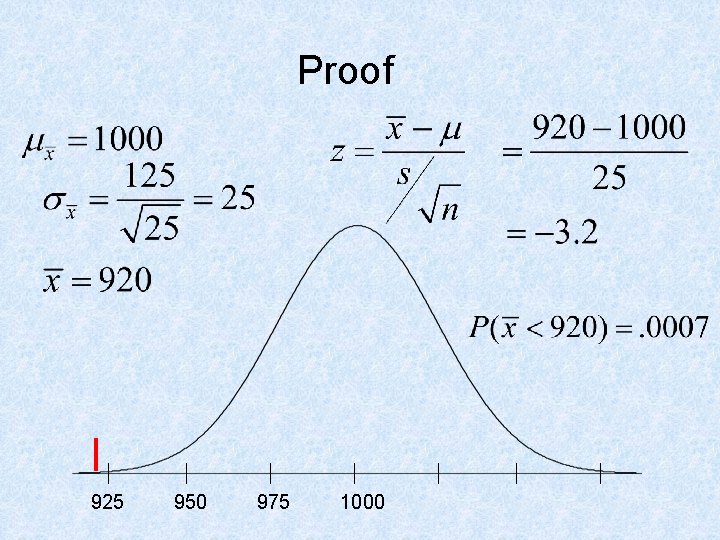
Proof 925 950 975 1000

Proof 925 950 975 1000

Definitions • A test of significance is a method for using sample data to make a decision about a population characteristic. • The null hypothesis, written H 0, is the starting value for the decision (i. e. H 0 : m = 1000). • The alternative hypothesis, written Ha, states what belief/claim we are trying to determine if statistically significant (Ha : m < 1000).

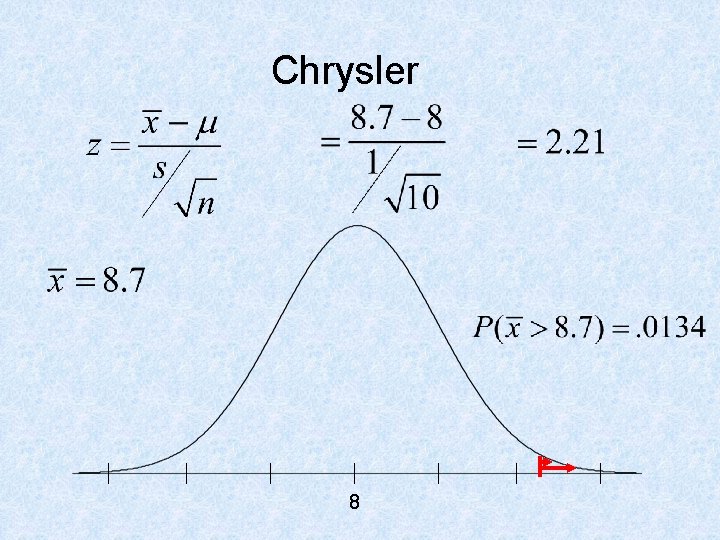
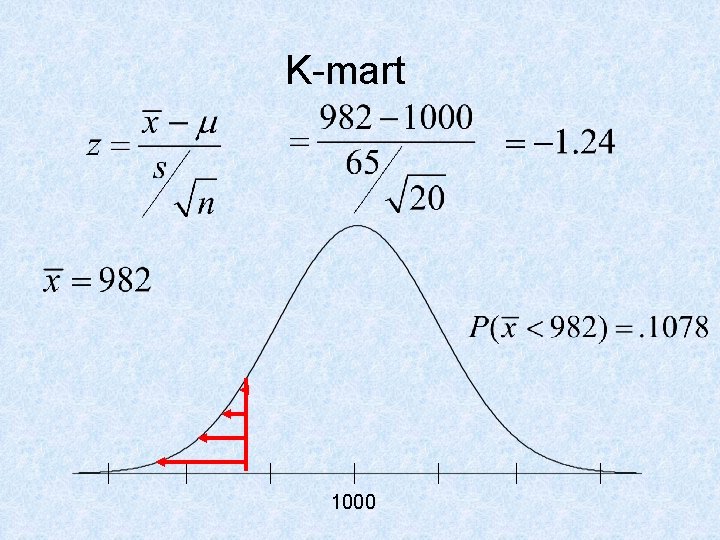
Examples • Chrysler Concord – H 0: m = 8 – H a: m > 8 • K-mart – H 0: m = 1000 – Ha: m < 1000

Chrysler 8

K-mart 1000

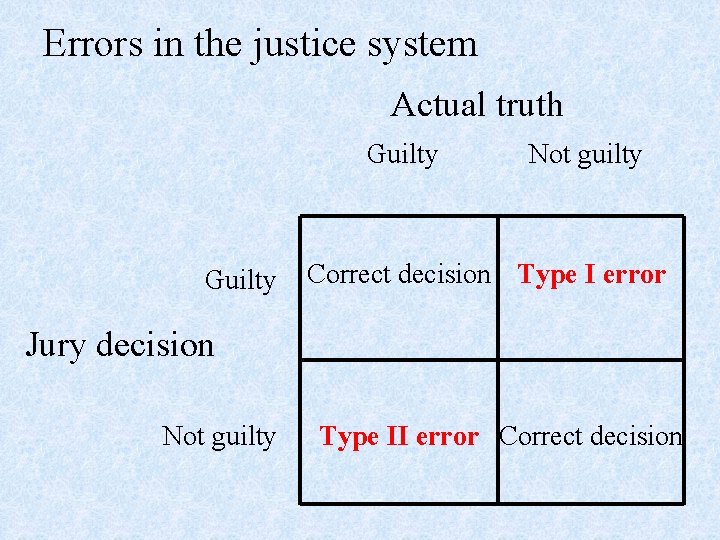
Phrasing our decision • In justice system, what is our null and alternative hypothesis? • H 0: defendant is innocent • Ha: defendant is guilty • What does the jury state if the defendant wins? • Not guilty • Why?

Phrasing our decision • H 0: defendant is innocent • Ha: defendant is guilty • If we have the evidence: – We reject the belief the defendant is innocent because we have the evidence to believe the defendant is guilty. • If we don’t have the evidence: – We fail to reject the belief the defendant is innocent because we do not have the evidence to believe the defendant is guilty.

Chrysler Concord • • H 0: m = 8 H a: m > 8 p-value =. 0134 We reject H 0 since the probability is so small there is enough evidence to believe the mean Concord time is greater than 8 seconds.

K-mart light bulb • • H 0: m = 1000 Ha: m < 1000 p-value =. 1078 We fail to reject H 0 since the probability is not very small there is not enough evidence to believe the mean lifetime is less than 1000 hours.

Remember: Inference procedure overview • • • State the procedure Define any variables Establish the conditions (assumptions) Use the appropriate formula Draw conclusions

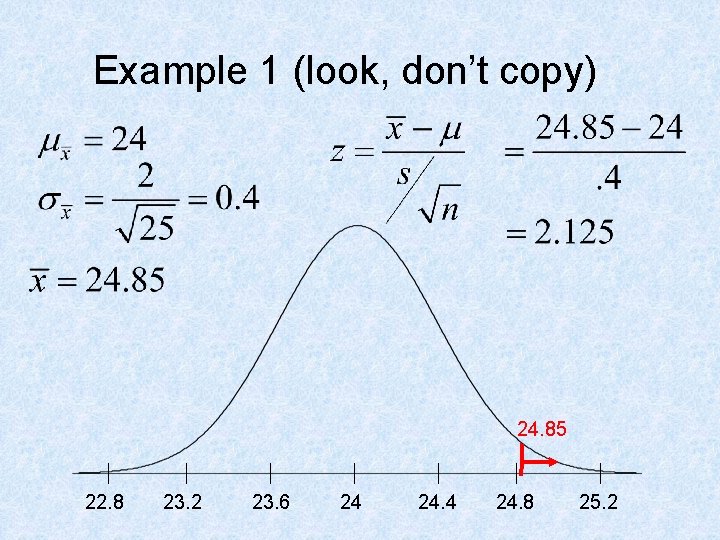
Test of Significance Example • A package delivery service claims it takes an average of 24 hours to send a package from New York to San Francisco. An independent consumer agency is doing a study to test the truth of the claim. Several complaints have led the agency to suspect that the delivery time is longer than 24 hours. Assume that the delivery times are normally distributed with standard deviation (assume s for now) of 2 hours. A random sample of 25 packages has been taken.

Example 1 test of significance m = true mean delivery time Ho: m = 24 Ha: m > 24 Given a random sample Given a normal distribution Safe to infer a population of at least 250 packages

Example 1 (look, don’t copy) 24. 85 22. 8 23. 2 23. 6 24 24. 8 25. 2

Example 1 test of significance m = true mean delivery time Ho: m = 24 Ha: m > 24 Given a random sample Given a normal distribution Safe to infer a population of at least 250 packages. let a =. 05

Example 1 test of significance m = true mean delivery time Ho: m = 24 Ha: m > 24 Given a random sample Given a normal distribution Safe to infer a population of at least 250 packages. We reject Ho. Since p-value<a there is enough evidence to believe the delivery time is longer than 24 hours.

Wording of conclusion revisit • If I believe the statistic is just too extreme and unusual (P-value < a), I will reject the null hypothesis. • If I believe the statistic is just normal chance variation (P-value > a), I will fail to reject the null hypothesis. reject p-value<a, there is We Ho, since the fail to reject p-value>a, there is not enough evidence to believe…(Ha in context…)

Example 3 test of significance m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

Familiar transition • What happened on day 2 of confidence intervals involving mean and standard deviation? • Switch from using z-scores to using the tdistribution. • What changes occur in the write up?

Example 3 test of significance m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample. Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

Example 3 t-test m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample. Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

Example 3 t-test m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

Example 3 t-test m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample. Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

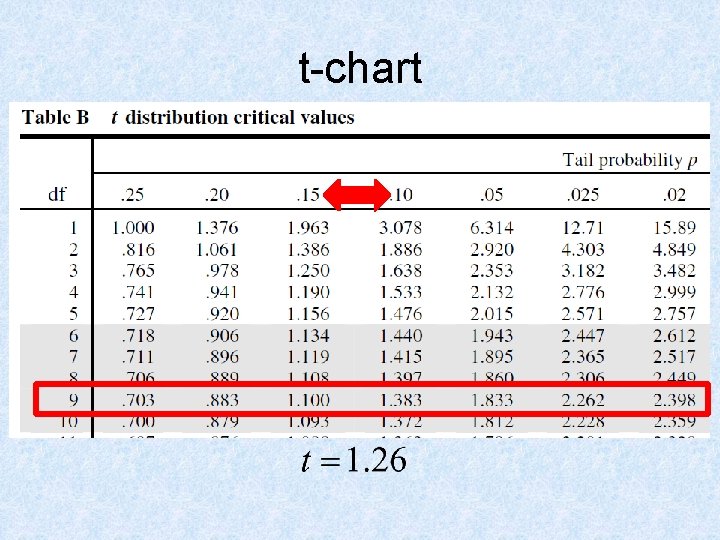
t-chart

Example 3 t-test m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample. Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

Example 3 t-test m = true mean distance Ho: m = 340 Ha: m > 340 Given random sample. Given normally distributed. Safe to infer a population of at least 100 missiles. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the mean distance traveled is more than 340 miles.

1 proportion z-test p = true proportion pure short Ho: p =. 25 Ha: p =. 25 Given a random sample. np = 1064(. 25) > 10 n(1–p) = 1064(1–. 25) > 10 Sample size is large enough to use normality Safe to infer a population of at least 10, 640 plants. We fail to reject Ho. Since p-value>a there is not enough evidence to believe the proportion of pure short is different than 25%.

Choosing a level of significance • How plausible is H 0? If H 0 represents a long held belief, strong evidence (small a) might be needed to dissolve the belief. • What are the consequences of rejecting H 0? The choice of a will be heavily influenced by the consequences of rejecting or failing to reject.

Errors in the justice system Actual truth Guilty Not guilty Correct decision Type I error Jury decision Not guilty Type II error Correct decision

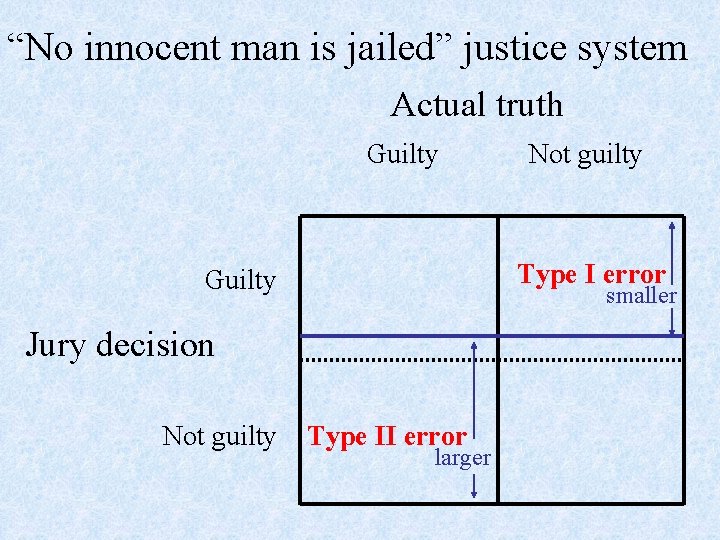
“No innocent man is jailed” justice system Actual truth Guilty Type I error Guilty smaller Jury decision Not guilty Type II error larger

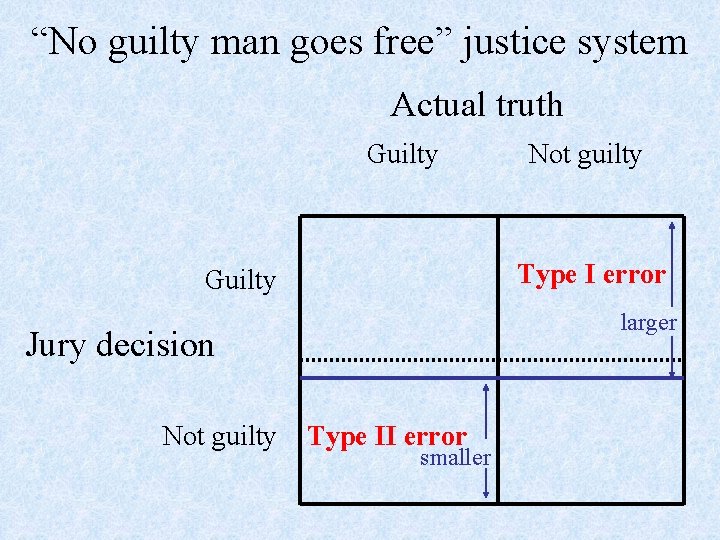
“No guilty man goes free” justice system Actual truth Guilty Type I error Guilty larger Jury decision Not guilty Type II error smaller

Errors in the justice system Actual truth Guilty (Ha true) Not guilty (H 0 true) Guilty Correct decision Type I error (reject H 0) Jury decision Not guilty Type II error Correct decision (fail to reject H 0)

Type I and Type II errors • If we believe Ha when in fact H 0 is true, this is a type I error. • If we believe H 0 when in fact Ha is true, this is a type II error. • Type I error: if we reject H 0 and it’s a mistake. • Type II error: if we fail to reject H 0 and it’s a mistake. APPLET

Type I and Type II example A distributor of handheld calculators receives very large shipments of calculators from a manufacturer. It is too costly and time consuming to inspect all incoming calculators, so when each shipment arrives, a sample is selected for inspection. Information from the sample is then used to test Ho: p =. 02 versus Ha: p <. 02, where p is the true proportion of defective calculators in the shipment. If the null hypothesis is rejected, the distributor accepts the shipment of calculators. If the null hypothesis cannot be rejected, the entire shipment of calculators is returned to the manufacturer due to inferior quality. (A shipment is defined to be of inferior quality if it contains 2% or more defectives. )

Type I and Type II example • Type I error: We think the proportion of defective calculators is less than 2%, but it’s actually 2% (or more). • Consequence: Accept shipment that has too many defective calculators so potential loss in revenue.

Type I and Type II example • Type II error: We think the proportion of defective calculators is 2%, but it’s actually less than 2%. • Consequence: Return shipment thinking there are too many defective calculators, but the shipment is ok.

Type I and Type II example • Distributor wants to avoid Type I error. Choose a =. 01 • Calculator manufacturer wants to avoid Type II error. Choose a =. 10

Concept of Power • Definition? • Power is the capability of accomplishing something… • The power of a test of significance is…

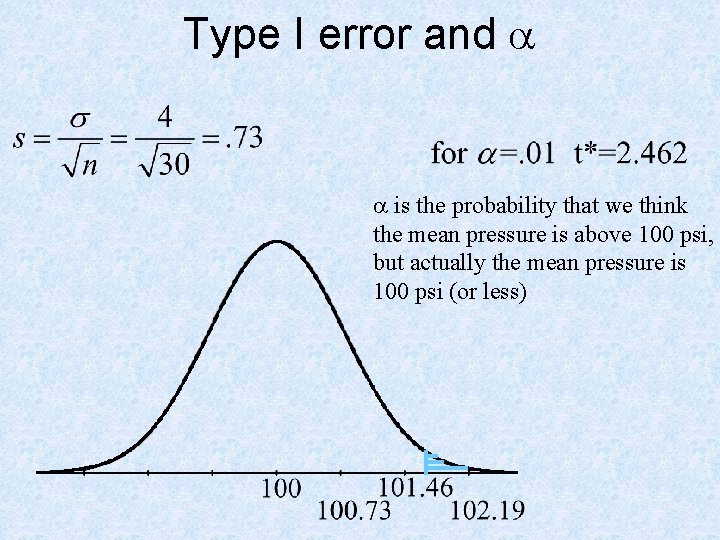
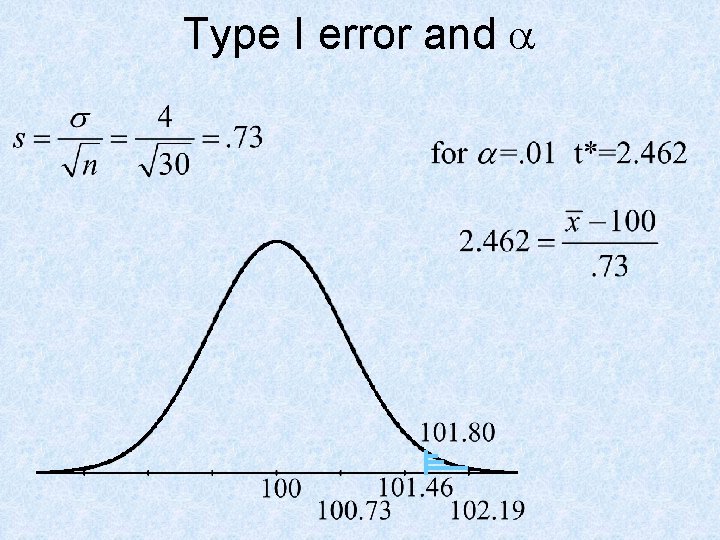
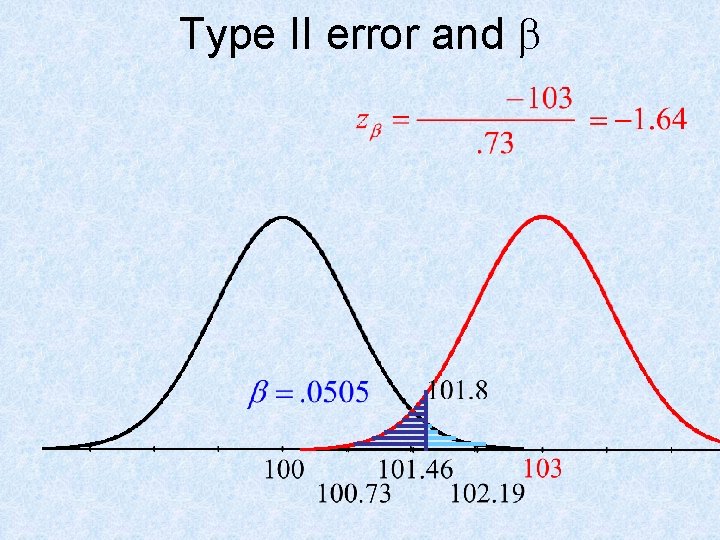
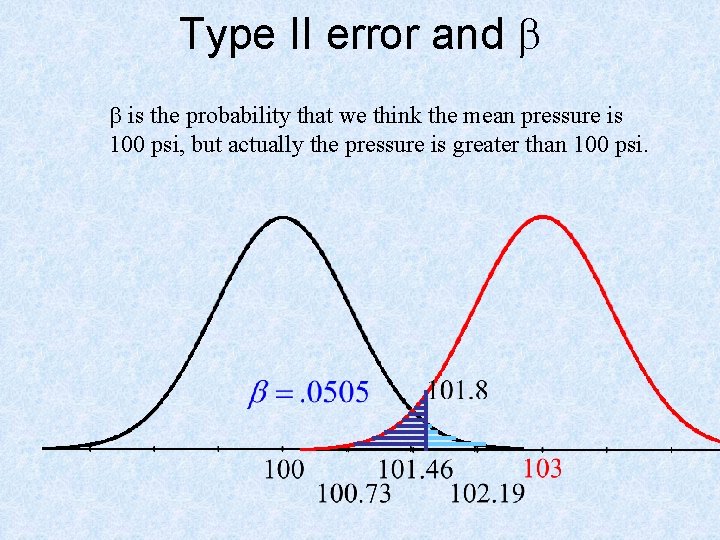
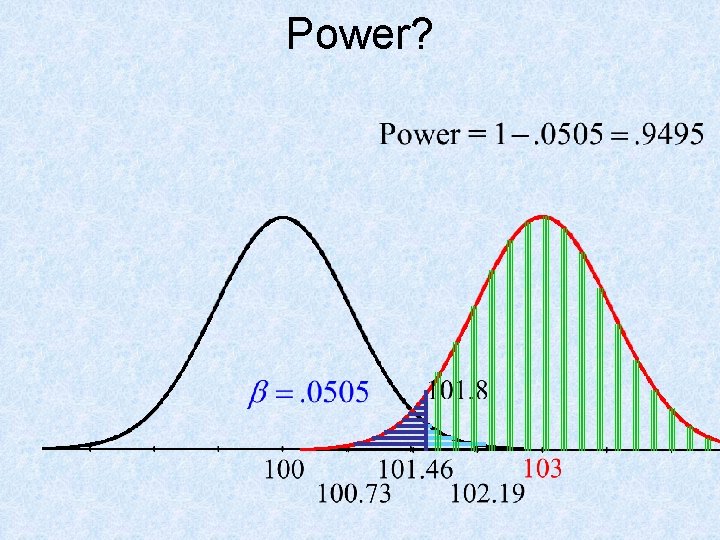
Power Example In a power generating plant, pressure in a certain line is supposed to maintain an average of 100 psi over any 4 - hour period. If the average pressure exceeds 103 psi for a 4 - hour period, serious complications can evolve. During a given 4 - hour period, thirty random measurements are to be taken. The standard deviation for these measurements is 4 psi (graph of data is reasonably normal), test Ho: m = 100 psi versus the alternative “new” hypothesis m = 103 psi. Test at the alpha level of. 01. Calculate a type II error and the power of this test. In context of the problem, explain what the power means.

Type I error and a a is the probability that we think the mean pressure is above 100 psi, but actually the mean pressure is 100 psi (or less)

Type I error and a

Type II error and b

Type II error and b b is the probability that we think the mean pressure is 100 psi, but actually the pressure is greater than 100 psi.

Power?

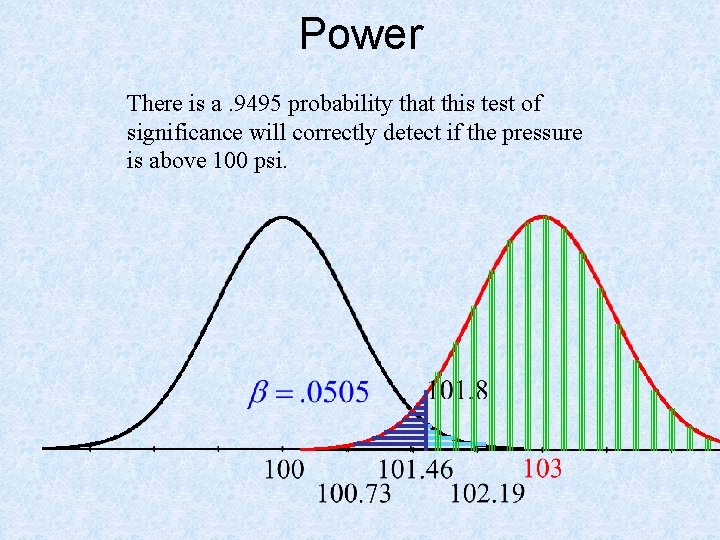
Power There is a. 9495 probability that this test of significance will correctly detect if the pressure is above 100 psi.

Concept of Power • The power of a test of significance is the probability that the null hypothesis will be correctly rejected. • Because the true value of m is unknown, we cannot know what the power is for m, but we are able to examine “what if” scenarios to provide important information. • Power = 1 – b

Effects on the Power of a Test • The larger the difference between the hypothesized value and the true value of the population characteristic, the higher the power. • The larger the significance level, a, the higher the power of the test. • The larger the sample size, the higher the power of the test. APPLET
 Hg 925/1995
Hg 925/1995 Force that opposes motion
Force that opposes motion 925 million
925 million Ace different help iq tests still
Ace different help iq tests still Types of significance tests
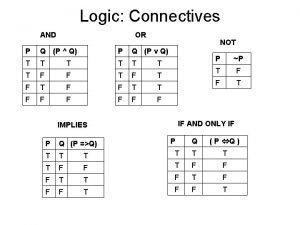
Types of significance tests Direct proof and indirect proof
Direct proof and indirect proof Direct proof and indirect proof
Direct proof and indirect proof Indirect proof assumption
Indirect proof assumption Direct proof and indirect proof
Direct proof and indirect proof Unit 2 logic and proof homework 7 algebraic proofs
Unit 2 logic and proof homework 7 algebraic proofs 2-5 algebraic proof
2-5 algebraic proof Lesson 4-7 introduction to coordinate proof
Lesson 4-7 introduction to coordinate proof Wigan lea mental maths
Wigan lea mental maths Tds apes
Tds apes Romberga tests
Romberga tests Dirty minded test questions
Dirty minded test questions Uil math practice tests elementary
Uil math practice tests elementary Uil general math practice test
Uil general math practice test Which shaft turns fastest
Which shaft turns fastest Shrek ordinary world
Shrek ordinary world Univariate analysis tests
Univariate analysis tests Gravity seriousness
Gravity seriousness Staar alt 2 released tests
Staar alt 2 released tests Recall example
Recall example Empty can test
Empty can test For what value of x is quadrilateral cdef a parallelogram?
For what value of x is quadrilateral cdef a parallelogram? Rorschach inkblot
Rorschach inkblot Qualitative tests for lipids
Qualitative tests for lipids Provincial achievement tests
Provincial achievement tests Hemastix color
Hemastix color Premarital tests or assessments
Premarital tests or assessments Prayers for before a test
Prayers for before a test Osas tide
Osas tide Osas science
Osas science P(aub) venn diagram
P(aub) venn diagram Iron deficiency anemia labs
Iron deficiency anemia labs Non-parametric t-test
Non-parametric t-test 8.3 proving parallelograms worksheet answers
8.3 proving parallelograms worksheet answers Wais
Wais Pros and cons of sternberg's triarchic theory
Pros and cons of sternberg's triarchic theory Eqao practice test
Eqao practice test Tests paramétriques
Tests paramétriques Elpac practice tests
Elpac practice tests Special test for ankle
Special test for ankle Fei dressage tests
Fei dressage tests Safety net drop tests must consist of a
Safety net drop tests must consist of a City & guilds evolve
City & guilds evolve Equilibrium non equilibrium test
Equilibrium non equilibrium test Why is it important to test installed equipment and devices
Why is it important to test installed equipment and devices