Chapter 8 Statistical inference Significance Tests About Hypotheses

Chapter 8 Statistical inference: Significance Tests About Hypotheses l Learn …. To use an inferential method called a Significance Test To analyze evidence that data provide To make decisions based on data Agresti/Franklin Statistics, 1 of 122

Two Major Methods for Making Statistical Inferences about a Population l Confidence Interval l Significance Test Agresti/Franklin Statistics, 2 of 122

Questions that Significance Tests Attempt to Answer l Does a proposed diet truly result in weight loss, on the average? l Is there evidence of discrimination against women in promotion decisions? l Does one advertising method result in better sales, on the average, than another advertising method? Agresti/Franklin Statistics, 3 of 122

ØSection 8. 1 What Are the Steps For Performing a Significance Test? Agresti/Franklin Statistics, 4 of 122

Hypothesis l l A hypothesis is a statement about a population, usually of the form that a certain parameter takes a particular numerical value or falls in a certain range of values The main goal in many research studies is to check whether the data support certain hypotheses Agresti/Franklin Statistics, 5 of 122

Significance Test l A significance test is a method of using data to summarize the evidence about a hypothesis l A significance test about a hypothesis has five steps Agresti/Franklin Statistics, 6 of 122

Step 1: Assumptions l A (significance) test assumes that the data production used randomization l Other assumptions may include: • Assumptions about the sample size • Assumptions about the shape of the population distribution Agresti/Franklin Statistics, 7 of 122

Step 2: Hypotheses l Each significance test has two hypotheses: • The null hypothesis is a statement that the parameter takes a particular value • The alternative hypothesis states that the parameter falls in some alternative range of values Agresti/Franklin Statistics, 8 of 122

Null and Alternative Hypotheses l The value in the null hypothesis usually represents no effect • The symbol Ho denotes null hypothesis l The value in the alternative hypothesis usually represents an effect of some type • The symbol Ha denotes alternative hypothesis Agresti/Franklin Statistics, 9 of 122

Null and Alternative Hypotheses l A null hypothesis has a single parameter value, such as Ho: p = 1/3 l An alternative hypothesis has a range of values that are alternatives to the one in Ho such as • Ha: p ≠ 1/3 or • Ha: p > 1/3 or • Ha: p < 1/3 Agresti/Franklin Statistics, 10 of 122

Step 3: Test Statistic l l The parameter to which the hypotheses refer has a point estimate: the sample statistic A test statistic describes how far that estimate (the sample statistic) falls from the parameter value given in the null hypothesis Agresti/Franklin Statistics, 11 of 122

Step 4: P-value l To interpret a test statistic value, we use a probability summary of the evidence against the null hypothesis, Ho • First, we presume that Ho is true • Next, we consider the sampling • distribution from which the test statistic comes We summarize how far out in the tail of this sampling distribution the test statistic falls Agresti/Franklin Statistics, 12 of 122

Step 4: P-value l We summarize how far out in the tail the test statistic falls by the tail probability of that value and values even more extreme • This probability is called a P-value • The smaller the P-value, the stronger the evidence is against Ho Agresti/Franklin Statistics, 13 of 122

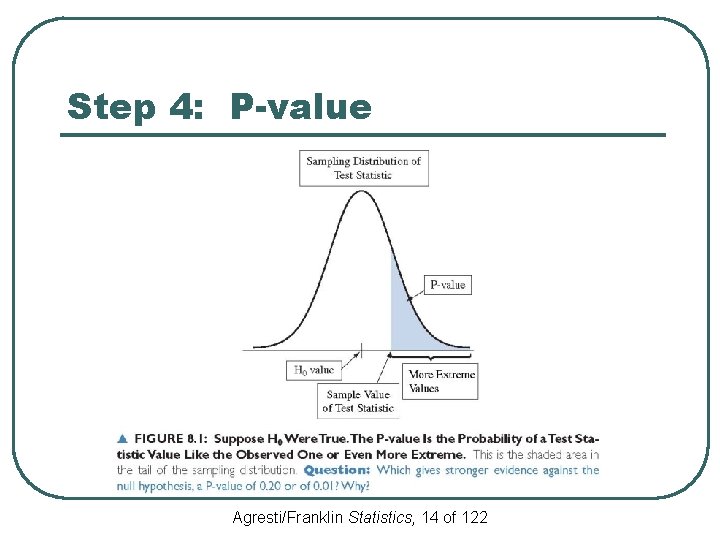
Step 4: P-value Agresti/Franklin Statistics, 14 of 122

Step 4: P-value l l The P-value is the probability that the test statistic equals the observed value or a value even more extreme It is calculated by presuming that the null hypothesis H is true Agresti/Franklin Statistics, 15 of 122

Step 5: Conclusion l The conclusion of a significance test reports the P-value and interprets what it says about the question that motivated the test Agresti/Franklin Statistics, 16 of 122

Summary: The Five Steps of a Significance Test 1. 2. 3. 4. 5. Assumption s Hypotheses Test Statistic P-value Conclusion Agresti/Franklin Statistics, 17 of 122

Is the Statement a Null Hypothesis or an Alternative Hypothesis? In Canada, the proportion of adults who favor legalize gambling is 0. 50. a. Null Hypothesis b. Alternative Hypothesis Agresti/Franklin Statistics, 18 of 122

Is the Statement a Null Hypothesis or an Alternative Hypothesis? a. b. The proportion of all Canadian college students who are regular smokers is less than 0. 24, the value it was ten years ago. Null Hypothesis Alternative Hypothesis Agresti/Franklin Statistics, 19 of 122

Ø Section 8. 4 Decisions and Types of Errors in Significance Tests Agresti/Franklin Statistics, 20 of 122

Type I and Type II Errors l When H 0 is true, a Type I Error occurs when H 0 is rejected l When H 0 is false, a Type II Error occurs when H 0 is not rejected Agresti/Franklin Statistics, 21 of 122

Significance Test Results Agresti/Franklin Statistics, 22 of 122

An Analogy: Decision Errors in a Legal Trial Agresti/Franklin Statistics, 23 of 122

P(Type I Error) = Significance Level α l Suppose H 0 is true. The probability of rejecting H 0, thereby committing a Type I error, equals the significance level, α, for the test. Agresti/Franklin Statistics, 24 of 122

P(Type I Error) l l We can control the probability of a Type I error by our choice of the significance level The more serious the consequences of a Type I error, the smaller α should be Agresti/Franklin Statistics, 25 of 122

Type I and Type II Errors l As P(Type I Error) goes Down, P(Type II Error) goes Up • The two probabilities are inversely related Agresti/Franklin Statistics, 26 of 122

A significance test about a proportion is conducted using a significance level of 0. 05. The test statistic is 2. 58. The P-value is 0. 01. If Ho is true, for what probability of a Type I error was the test designed? a. . 01 b. . 05 c. 2. 58 d. . 02 Agresti/Franklin Statistics, 27 of 122

A significance test about a proportion is conducted using a significance level of 0. 05. The test statistic is 2. 58. The P-value is 0. 01. If this test resulted in a decision error, what type of error was it? a. Type I b. Type II Agresti/Franklin Statistics, 28 of 122