INTEGRATION Pengertian Integral Calculus Aturan Trapezoidal Aturan Simpson

INTEGRATION • • • Pengertian Integral Calculus Aturan Trapezoidal Aturan Simpson 1/3 Integrasi Romberg Aturan Gauss-Quad Mengintegrasikan Fungsi Diskrit

INTEGRATION Definisi Integrasi adalah menggabungkan bagian-bagian sehingga mereka bekerja bersama-sama atau bentuk keseluruhan. Secara matematis, integrasi berguna untuk menemukan daerah di bawah kurva dari satu titik ke titik lain. Hal ini diwakili oleh : dimana simbol adalah tanda integral, dan a dan b adalah batas bawah dan batas integrasi, fungsi f adalah integran dari integral, dan x adalah variabel integrasi. Gambar 1 merupakan demonstrasi grafis dari konsep.

PENGERTIAN INTEGRASI Pendekatan terhadap integral • Metode ini memotong interval [a, b] menjadi sebuah partisi dengan subinterval n yang sama panjang untuk i = 0, 1, 2, …, n • Algoritma: bagaimana mendapatkan supremum dan infimum dari f(x) pada setiap interval • Pendekatan integrasi: • Error:

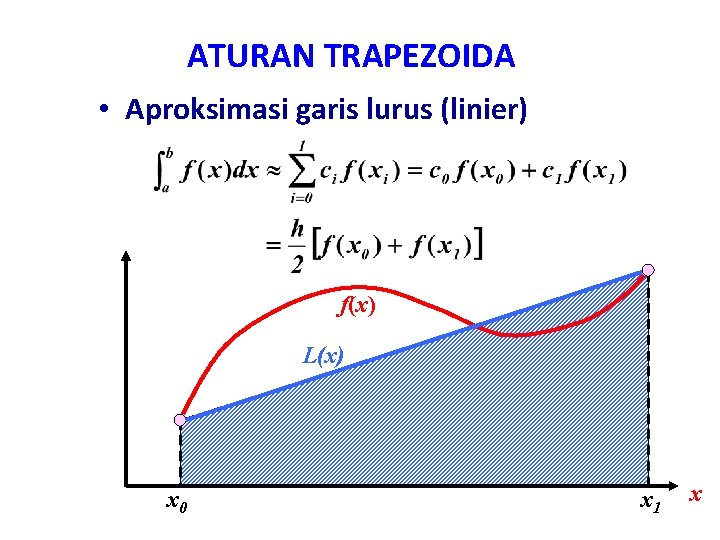
ATURAN TRAPEZOIDA • Aproksimasi garis lurus (linier) f(x) L(x) x 0 x 1 x

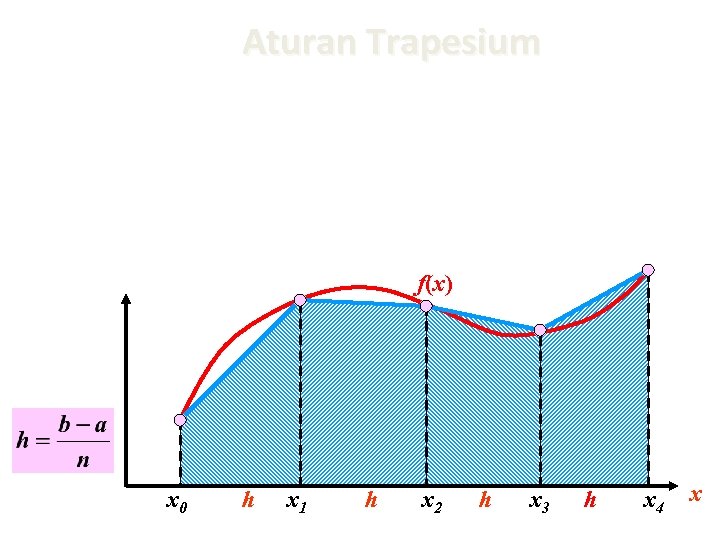
Aturan Trapesium f(x) x 0 h x 1 h x 2 h x 3 h x 4 x

ATURAN Trapezoida

ATURAN TRAPEZOIDA • Definisikan y=f(x) • Tentukan batas bawah (a) dan batas integrasi (b) • Tentukan jumlah pembagi n • Hitung h=(b-a)/n • Hitung

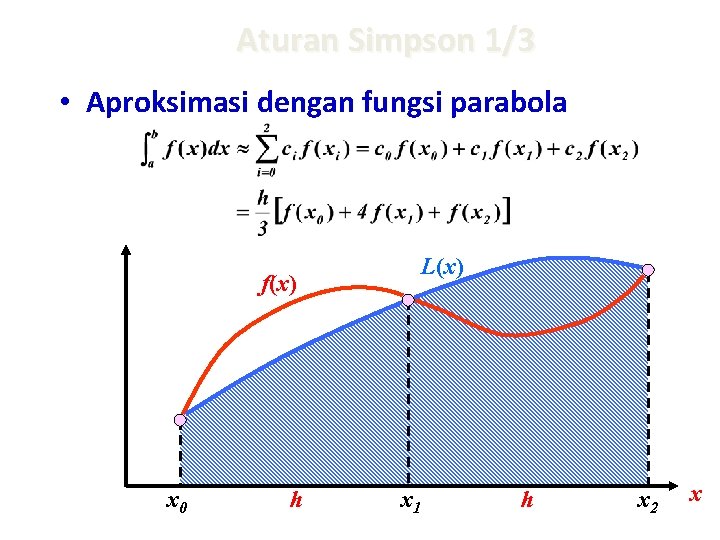
Aturan Simpson 1/3 • Aproksimasi dengan fungsi parabola L(x) f(x) x 0 h x 1 h x 2 x

Aturan Simpson 1/3

Aturan Simpson 1/3

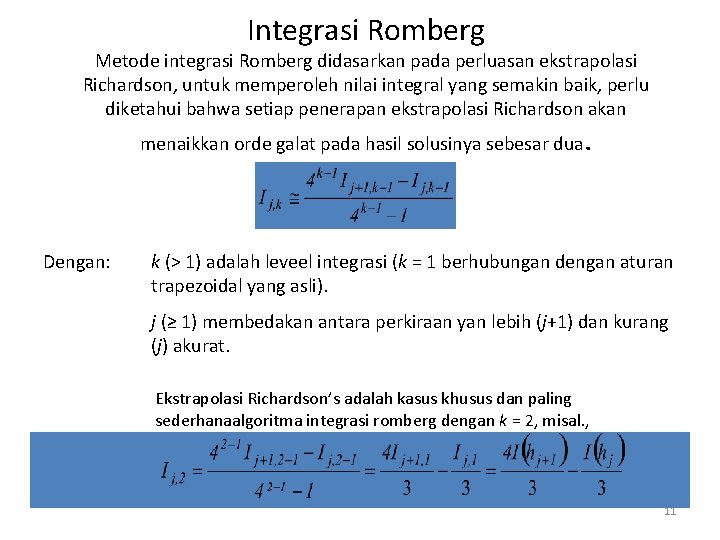
Integrasi Romberg Metode integrasi Romberg didasarkan pada perluasan ekstrapolasi Richardson, untuk memperoleh nilai integral yang semakin baik, perlu diketahui bahwa setiap penerapan ekstrapolasi Richardson akan menaikkan orde galat pada hasil solusinya sebesar dua Dengan: . k (> 1) adalah leveel integrasi (k = 1 berhubungan dengan aturan trapezoidal yang asli). j (≥ 1) membedakan antara perkiraan yan lebih (j+1) dan kurang (j) akurat. Ekstrapolasi Richardson’s adalah kasus khusus dan paling sederhanaalgoritma integrasi romberg dengan k = 2, misal. , 11

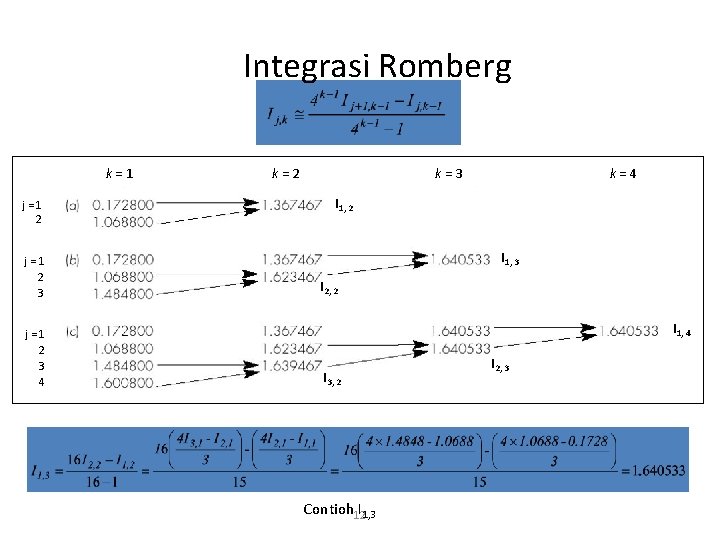
Integrasi Romberg k=1 j=1 2 3 4 k=2 k=3 k=4 I 1, 2 I 1, 3 I 2, 2 I 1, 4 I 3, 2 Contioh 12 I 1, 3 I 2, 3

Metode Integrasi Gauss • Metode Newton Code (Trapezoida, Simpson) berdasarkan titik 2 data diskrit. Dengan batasan : – H sama – Luas dihitung dari a sampai b • Mengakibatkan error yang dihasilkan cukup besar.

Metode Integrasi Gauss • Misal menghitung Luas dengan metode trapezoida dengan selang [-1, 1] • Persamaan ini dapat ditulis (disebut pers Kuadratur Gauss) • Misal x 1=-1, x 2=1 dan c 1=c 2=1 menjadi m. trapezoida • Karena x 1, x 2, , c 1 dan c 2 sembarang maka kita harus memilih nilai tersebut sehingga error integrasinya min

Metode Integrasi Gauss • Bagaimana mencari x 1, x 2, , c 1 dan c 2 Persamaan dibawah ini dianggap memenuhi secara tepat bila empat polinom berikut dijadikan fungsi integral pada interval integrasi [-1, 1] • f(x) = 1 ; f(x) = x 2 ; f(x) = x 3 Didapat

Mengintegrasikan Fungsi Diskrit Metode Spline

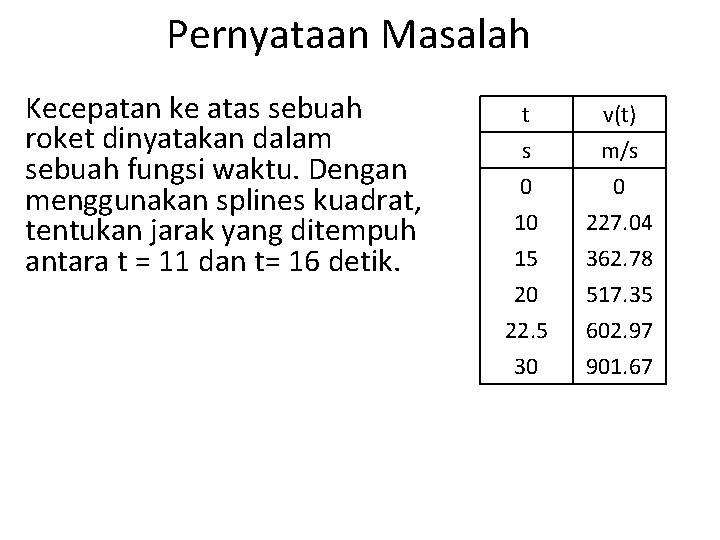
Pernyataan Masalah Kecepatan ke atas sebuah roket dinyatakan dalam sebuah fungsi waktu. Dengan menggunakan splines kuadrat, tentukan jarak yang ditempuh antara t = 11 dan t= 16 detik. t s 0 10 v(t) m/s 0 227. 04 15 20 22. 5 30 362. 78 517. 35 602. 97 901. 67

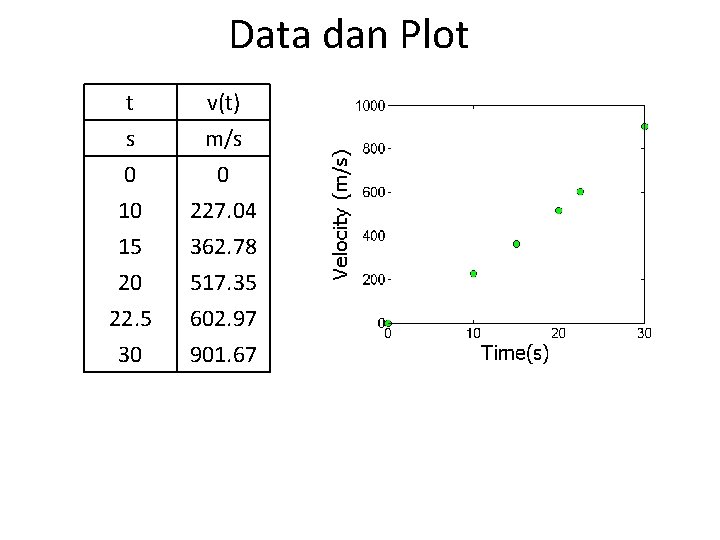
Data dan Plot t s 0 10 v(t) m/s 0 227. 04 15 20 22. 5 30 362. 78 517. 35 602. 97 901. 67

Solusi

Jarak dari Kecepatan

Jarak dari Kecepatan

Mengintegrasikan Fungsi Diskrit Metode Regresi

Kecilkan trunnion Fit ke Hub

Apakah Kontraksi ini cukup? Besarnya kontraksi diperlukan dalam trunnion adalah 0, 015 "atau lebih.

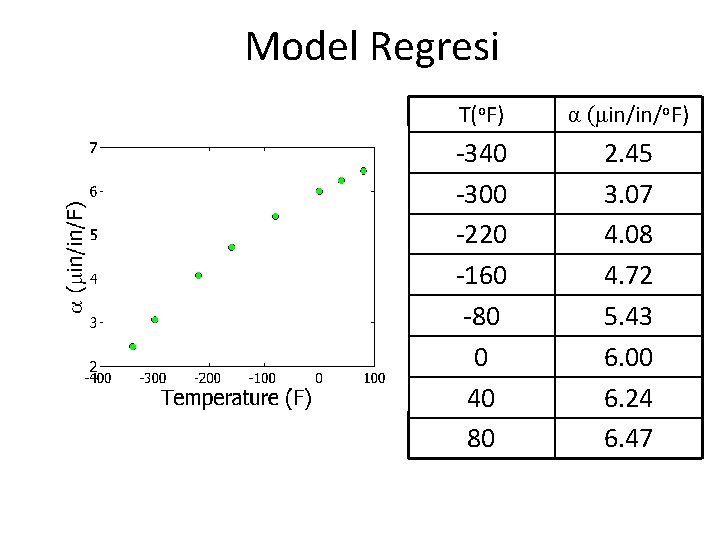
Bagaimana kita menemukan kontraksi ? Ta = 80 o. F Tc = -108 o. F D = 12. 363" T(o. F) α (μin/in/o. F) -340 -300 -220 -160 -80 0 40 80 2. 45 3. 07 4. 08 4. 72 5. 43 6. 00 6. 24 6. 47

Model Regresi T(o. F) α (μin/in/o. F) -340 -300 -220 -160 -80 0 40 80 2. 45 3. 07 4. 08 4. 72 5. 43 6. 00 6. 24 6. 47

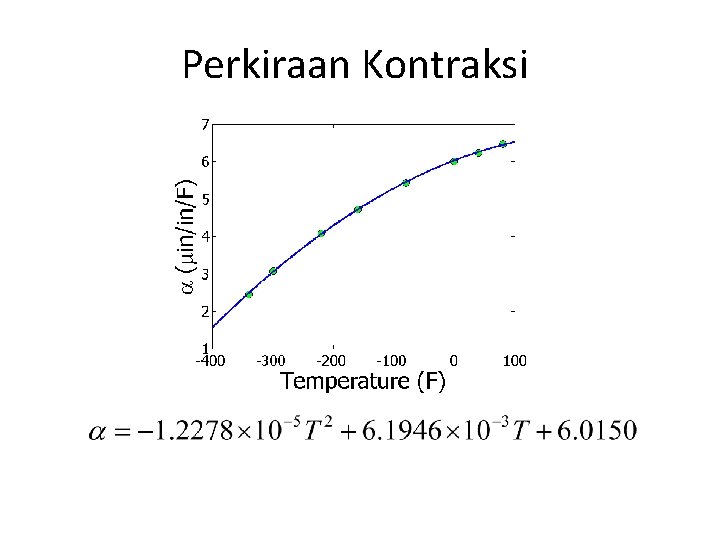
Perkiraan Kontraksi

Menghitung Kontraksi Ta = 80 o. F, Tc = -108 o. F, D = 12. 363" Besarnya kontraksi diperlukan dalam trunnion adalah 0, 015 "atau lebih.