Integral Pengertian Integral l Jika Fx adalah fungsi














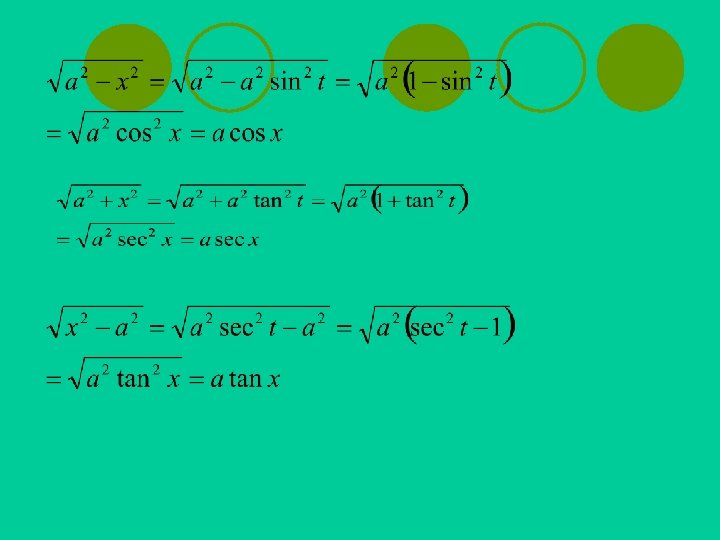

![Integral Tertentu l Jika fungsi f terdefinisi pada interval [a, b], maka adalah integral Integral Tertentu l Jika fungsi f terdefinisi pada interval [a, b], maka adalah integral](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-17.jpg)


![Teorema 1 Kelinearan l Jika f dan g terintegralkan pada interval [a, b] dan Teorema 1 Kelinearan l Jika f dan g terintegralkan pada interval [a, b] dan](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-20.jpg)
![Teorema 2 l Perubahan batas l Jika f terintegralkan pada interval [a, b] maka: Teorema 2 l Perubahan batas l Jika f terintegralkan pada interval [a, b] maka:](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-21.jpg)



















- Slides: 45

Integral

Pengertian Integral l Jika F(x) adalah fungsi umum yang bersifat F’(x) = f(x), l maka F(x) merupakan antiturunan atau integral dari f(x).

Pengintegralan fungsi f(x) terhadap x dinotasikan sebagai berikut : notasi integral (yang diperkenalkan oleh Leibniz, seorang matematikawan Jerman) l f(x) fungsi integran l F(x) fungsi integral umum yang bersifat F’(x) f(x) l c konstanta pengintegralan l

l Jika f ‘(x) = xn, maka ≠ -1, dengan c sebagai konstanta , n

Integral Tak Tentu l apabila terdapat fungsi F(x) yang dapat didiferensialkan pada interval sedemikian hingga maka antiturunan dari f(x) adalah F(x) + c l Secara matematis, ditulis

l di mana l l f(x) lc Lambang integral yang menyatakan operasi antiturunan Fungsi integran, yaitu fungsi yang dicari antiturunannya Konstanta

Teorema 1 l Jika n bilangan rasional dan n ≠ 1, maka , c adalah konstanta.

Teorema 2 l Jika f fungsi yang terintegralkan dan k suatu konstanta, maka

Teorema 3 l Jika f dan g fungsi-fungsi yang terintegralkan, maka

Teorema 4 l Jika f dan g fungsi-fungsi yang terintegralkan, maka

Teorema 5 l Aturan integral substitusi l Jika u suatu fungsi yang dapat didiferensialkan dan r suatu bilangan rasional tak nol maka , dimana c adalah konstanta dan r ≠ -1.

Teorema 6 l Aturan integral parsial l Jika u dan v fungsi-fungsi yang dapat didiferensialkan, maka

Teorema 7 l Aturan integral trigonometri l dimana c adalah konstanta.

Integral dengan bentuk l Pengintegralan bentuk dilakukan dengan menggunakan subtisusi dengan x = a sin t, x = a tan t , x = a sec t. Sehingga diperoleh bentuk-bentuk seperti ini
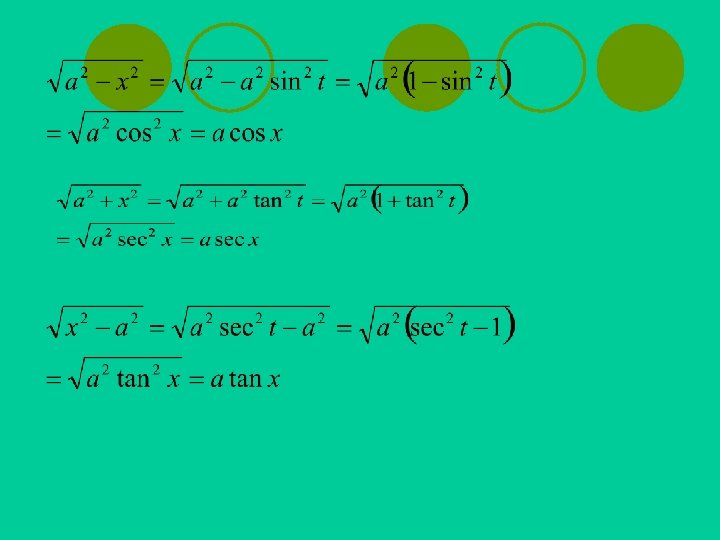

Ingat :
![Integral Tertentu l Jika fungsi f terdefinisi pada interval a b maka adalah integral Integral Tertentu l Jika fungsi f terdefinisi pada interval [a, b], maka adalah integral](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-17.jpg)
Integral Tertentu l Jika fungsi f terdefinisi pada interval [a, b], maka adalah integral tertentu terhadap fungsi f dari a ke b. Pengintegralannya dituliskan sebagai berikut.

l dengan: f(x) a b fungsi integran batas bawah batas

Teorema Dasar Kalkulus l Jika f kontinu pada interval dan andaikan F sembarang antiturunan dari f pada interval tersebut, maka
![Teorema 1 Kelinearan l Jika f dan g terintegralkan pada interval a b dan Teorema 1 Kelinearan l Jika f dan g terintegralkan pada interval [a, b] dan](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-20.jpg)
Teorema 1 Kelinearan l Jika f dan g terintegralkan pada interval [a, b] dan k suatu konstanta, maka
![Teorema 2 l Perubahan batas l Jika f terintegralkan pada interval a b maka Teorema 2 l Perubahan batas l Jika f terintegralkan pada interval [a, b] maka:](https://slidetodoc.com/presentation_image_h/8914b4edf46ff0d97cbd69f7de757389/image-21.jpg)
Teorema 2 l Perubahan batas l Jika f terintegralkan pada interval [a, b] maka:

Teorema 3 Teorema penambahan interval l Jika f terintegralkan pada suatu interval yang memuat tiga titik a, b, dan c, Maka

Teorema 4 Kesimetrian l Jika f fungsi genap, maka l l Jika f fungsi ganjil, maka

Menentukan Luas Daerah 1. Menentukan Luas Daerah di Atas Sumbu-x Misalkan R daerah yang dibatasi oleh kurva y = f(x), sumbu-x, garis x = a, dan garis x = b, dengan f(x) ≥ 0 pada [a, b], maka luas daerah R adalah sebagai berikut.

Grafik kurva di atas sumbu -x y = f(x) L(R) a b

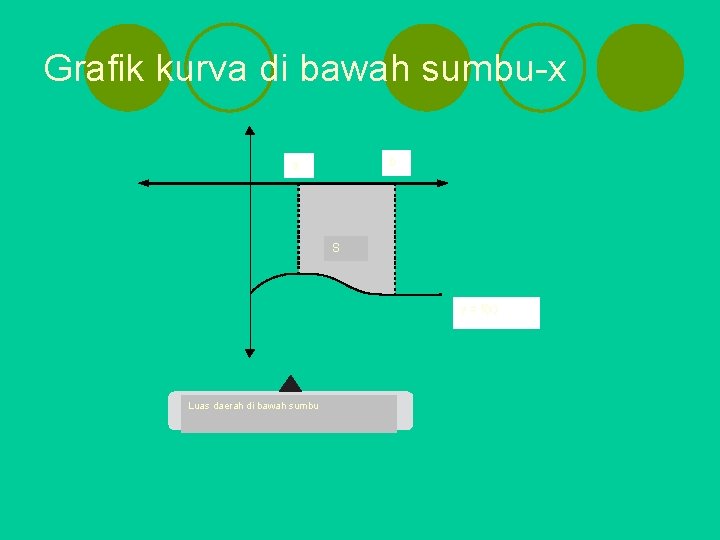
2. Menentukan Luas Daerah di Bawah Sumbu-x Misalnya S daerah yang dibatasi oleh kurva y = f(x), sumbu-x, garis x = a, dan garis x = b, dengan f(x) ≤ 0 pada [a, b], seperti yang telah dibahas di subbab D. 1, maka luas daerah S adalah

Grafik kurva di bawah sumbu-x b a S y = f(x) Luas daerah di bawah sumbu

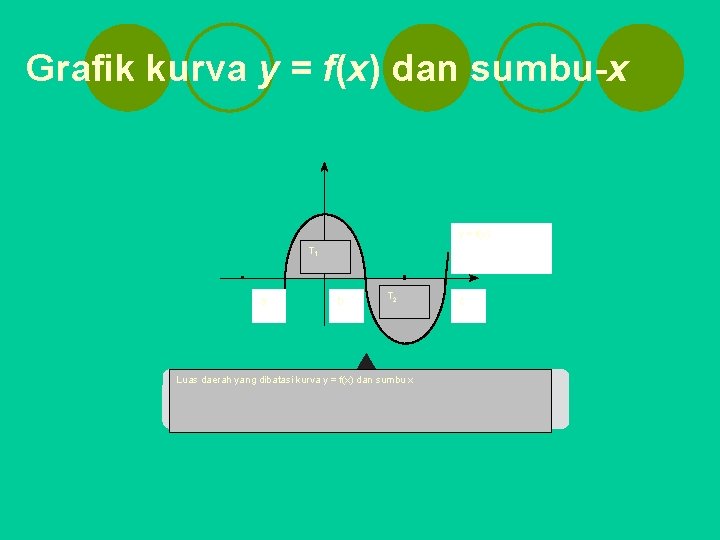
3. Menentukan Luas Daerah yang Terletak Dibatasi Kurva y = f(x) dan sumbu-x l Misalkan T daerah yang dibatasi oleh kurva y = f(x), sumbu-x, garis x = a, dan garis x = c, dengan f(x) ≥ 0 pada [a, b] dan f(x) ≤ 0 pada [b, c], maka luas daerah T adalah

l Rumus ini didapat dengan membagi daerah T menjadi T 1 dan T 2 masing pada interval [a, b] dan [b, c]. Kalian dapat menentukan luas T 1 sebagai luas darah yang terletak di atas sumbu-x dan luas T 2 sebagai luas daerah yang terletak di bawah sumbu-x.

Grafik kurva y = f(x) dan sumbu-x y = f(x) T 1 a b T 2 Luas daerah yang dibatasi kurva y = f(x) dan sumbu x c

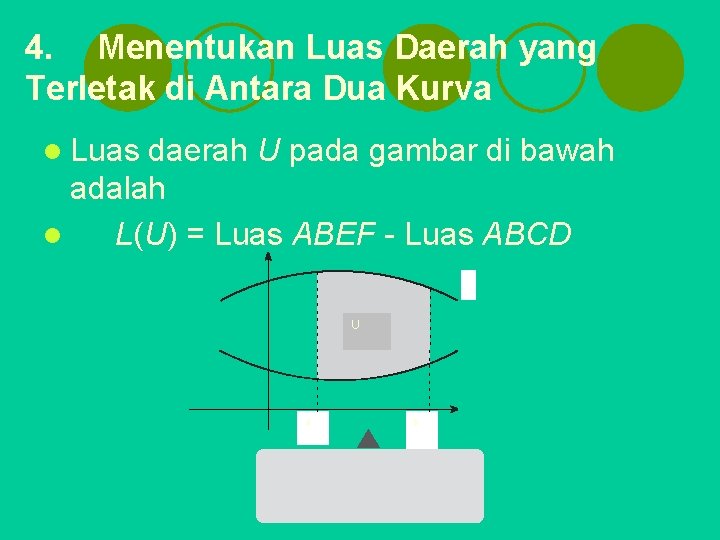
4. Menentukan Luas Daerah yang Terletak di Antara Dua Kurva l Luas daerah U pada gambar di bawah adalah l L(U) = Luas ABEF - Luas ABCD U a b

l ABEF adalah daerah yang dibatasi oleh kurva y 1 = f(x), x = a, x = b, dan y = 0 sehingga Luas ABEF l Adapun ABCD adalah daerah yang dibatasi oleh kurva y 2 = g(x), x = a, x = b, dan y = 0 sehingga Luas ABEF

l Dengan demikian, luas daerah U adalah

Menentukan volume Benda Putar l 1. Menentukan Volume Benda Putar yang Diputar Mengelilingi Sumbu-x l Secara umum, volume dinyatakan sebagai luas alas dikali tinggi. Secara matematis, ditulis V=A. h

l perhatikan sebuah benda yang bersifat bahwa penampang-penampang tegak lurusnya pada suatu garis tertentu memiliki luas tertentu. Misalnya, garis tersebut adalah sumbu-x dan andaikan luas penampang di x adalah A(x) dengan a ≤ x ≤ b. Bagi selang [a, b] dengan titik-titik bagi a = x 0 < x 1< x 2<. . . < xn = b.

l Melalui titik-titik ini, luas bidang tegak lurus pada sumbu-x, sehingga diperoleh pemotongan benda menjadi lempengan yang tipis-tipis. Volume suatu lempengan ini dapat dianggap sebagai volume tabung, yaitu , dengan.

Kita dapatkan kemudian akan menjadi

l A(x) adalah luas alas benda putar, oleh karena alas benda putar ini berupa lingkaran, maka jari-jari yang dimaksud merupakan sebuah fungsi dalam xi misalnya f(x). Dengan demikian volume benda putar dapat dinyatakan sebagai

l Misalkan R daerah yang dibatasi oleh grafik fungsi f(x), sumbu-x, garis x = a, garis x = b, dengan a < b, maka volume benda putar yang diperoleh dengan memutar daerah R mengelilingi sumbu-x adalah

2. Menentukan Volume Benda Putar yang Diputar Mengelilingi Sumbu-y l Misalkan S daerah yang dibatasi oleh grafik fungsi x f(y), sumbu-y, garis x = a, garis x = b, dengan a < b, maka volume benda putar yang diperoleh dengan memutar daerah S mengelilingi sumbu-y adalah V.

Grafik Volume Benda Putar yang Diputar Mengelilingi Sumbu-y Volume benda putar mengelilingi sumbu y

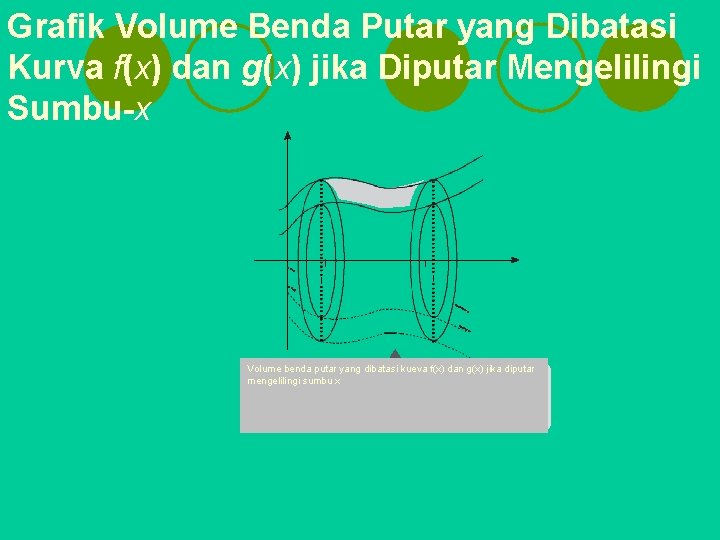
3. Menentukan Volume Benda Putar yang Dibatasi Kurva f(x) dan g(x) jika Diputar Mengelilingi Sumbu-x l Daerah yang dibatasi oleh kurva f(x) dan g(x) dengan , pada interval [a, b] diputar mengelilingi sumbu-x seperti yang telah dijelaskan di subbab E. 1, maka volume benda putar yang diperoleh adalah sebagai berikut.

Grafik Volume Benda Putar yang Dibatasi Kurva f(x) dan g(x) jika Diputar Mengelilingi Sumbu-x Volume benda putar yang dibatasi kueva f(x) dan g(x) jika diputar mengelilingi sumbu x

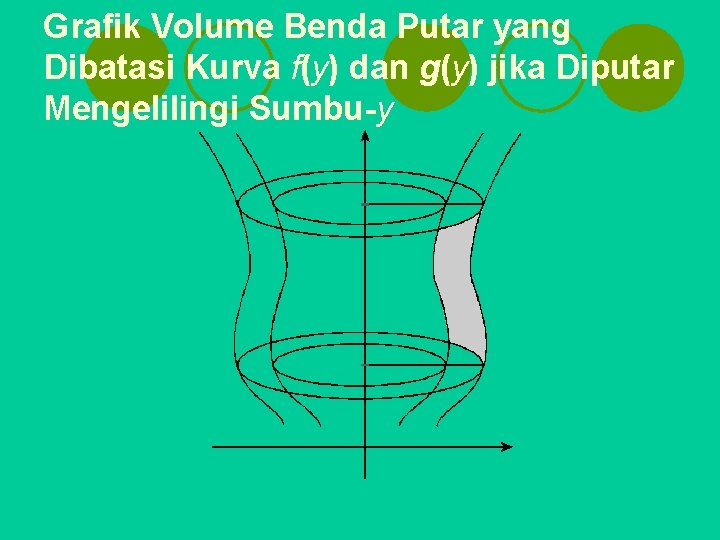
4. Menentukan Volume Benda Putar yang Dibatasi Kurva f(y) dan g(y) jika Diputar Mengelilingi Sumbu-y l Jika daerah yang dibatasi oleh kurva f(y) dan g(y) dengan pada interval [a, b] diputar mengelilingi sumbu-y. Seperti yang telah l dijelaskan di subbab E. 1, maka volume benda putar yang diperoleh adalah sebagai berikut.

Grafik Volume Benda Putar yang Dibatasi Kurva f(y) dan g(y) jika Diputar Mengelilingi Sumbu-y
 Contoh soal fungsi transenden
Contoh soal fungsi transenden Rumus cepat fungsi komposisi
Rumus cepat fungsi komposisi Jika fungsi permintaan dilambangkan dengan fungsi q = 12
Jika fungsi permintaan dilambangkan dengan fungsi q = 12 Fungsi linear dan non linear
Fungsi linear dan non linear Pengertian limit melalui pengamatan grafik fungsi
Pengertian limit melalui pengamatan grafik fungsi Jika fungsi permintaan suatu produk adalah p=36-4q
Jika fungsi permintaan suatu produk adalah p=36-4q Jika f(x) adalah fungsi kontinu dengan f(4) = 5 maka
Jika f(x) adalah fungsi kontinu dengan f(4) = 5 maka Tentukan konstanta c agar fungsi
Tentukan konstanta c agar fungsi Fungsi yang termasuk fungsi eksponensial adalah
Fungsi yang termasuk fungsi eksponensial adalah Trigonometri a
Trigonometri a Integrals
Integrals Integral and non integral citation
Integral and non integral citation Non integral citation
Non integral citation Integral garis dan integral permukaan
Integral garis dan integral permukaan Exchange difference of integral foreign operation is
Exchange difference of integral foreign operation is Integral dx
Integral dx Jika f x =
Jika f x = Kerbau dipegang talinya manusia dipegang janjinya maksud
Kerbau dipegang talinya manusia dipegang janjinya maksud Poset lattice
Poset lattice Struktur algoritma sequence
Struktur algoritma sequence Diketahui (x+3) dan (x-2) merupakan faktor dari p(x)
Diketahui (x+3) dan (x-2) merupakan faktor dari p(x) Kebalikan integral
Kebalikan integral Aturan fungsi invers
Aturan fungsi invers Apa itu mutiple queue dan one way list
Apa itu mutiple queue dan one way list Fungsi fungsi tes
Fungsi fungsi tes Contoh fungsi penerimaan
Contoh fungsi penerimaan Penerapan fungsi non linier dalam ekonomi
Penerapan fungsi non linier dalam ekonomi Rumus fungsi linear penawaran
Rumus fungsi linear penawaran Contoh fungsi non linear
Contoh fungsi non linear Cara menghitung titik pulang pokok
Cara menghitung titik pulang pokok Scope administrasi pendidikan
Scope administrasi pendidikan Fungsi dari icon crop adalah....
Fungsi dari icon crop adalah.... Gunadarma
Gunadarma Tentukan turunan fungsi fungsi berikut y=12/x⁷
Tentukan turunan fungsi fungsi berikut y=12/x⁷ Fungsi komposisi dan fungsi invers
Fungsi komposisi dan fungsi invers Pengertian integral tentu
Pengertian integral tentu Contoh integral tak wajar
Contoh integral tak wajar Fungsi hlook up digunakan untuk... *
Fungsi hlook up digunakan untuk... * Fungsi komposisi
Fungsi komposisi Pengertian, fungsi dan jenis lingkungan pendidikan
Pengertian, fungsi dan jenis lingkungan pendidikan Pppk petra kota surabaya jawa timur
Pppk petra kota surabaya jawa timur Linier adalah
Linier adalah Grafik limit fungsi
Grafik limit fungsi Bentuk eksplisit
Bentuk eksplisit Apakah peran dan fungsi itu sama
Apakah peran dan fungsi itu sama Pengertian fungsi polinom
Pengertian fungsi polinom