1 Chapter 10 Vector Integral Calculus Integral Theorems

























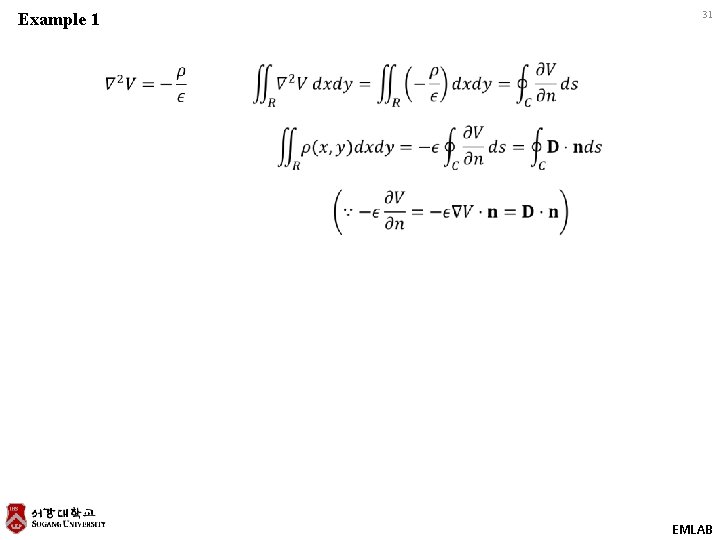
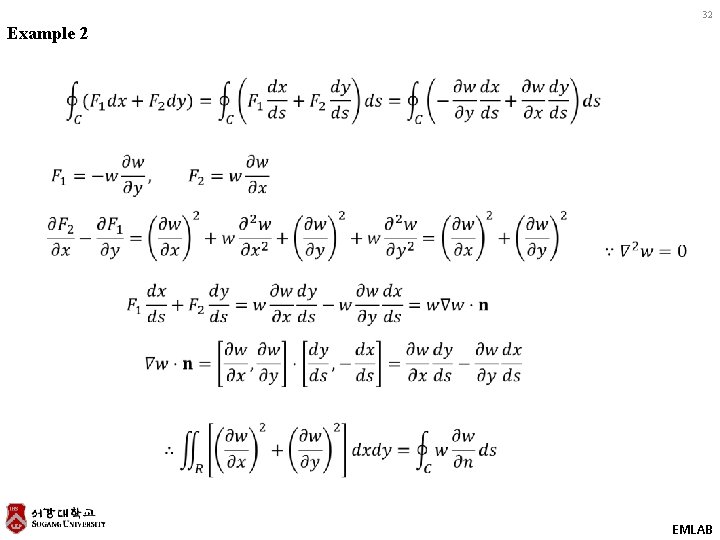















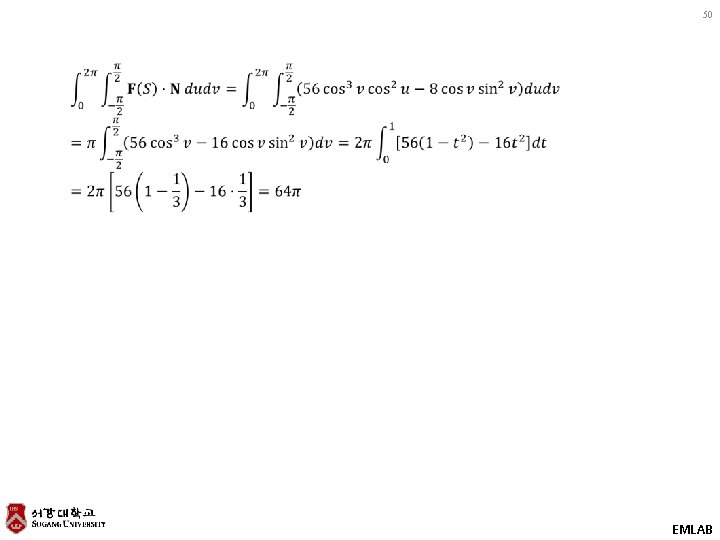

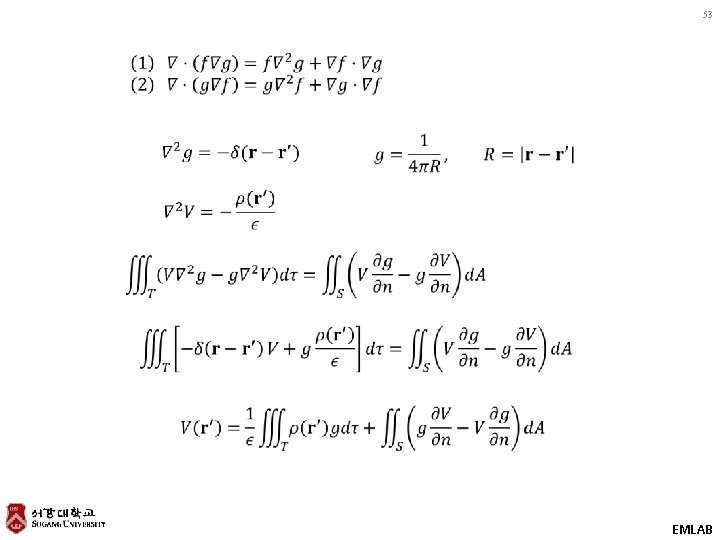


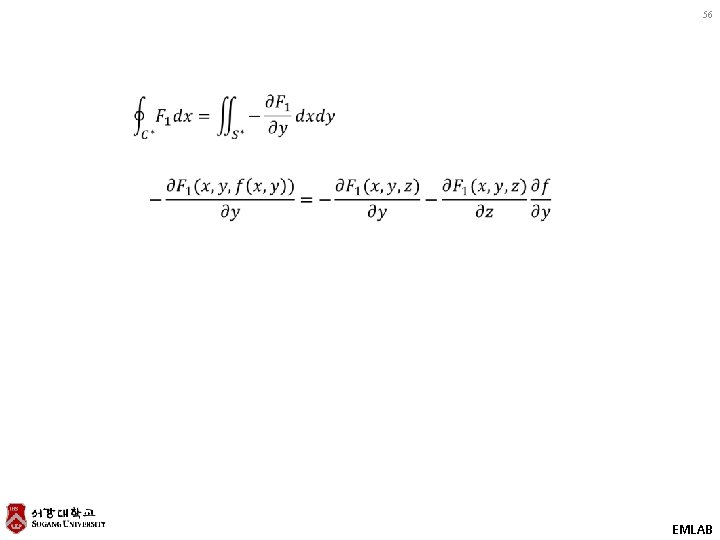

- Slides: 57

1 Chapter 10. Vector Integral Calculus. Integral Theorems EMLAB

1. 1 Line Integrals 2 Definition and Evaluation of Line Integrals For closed path : EMLAB

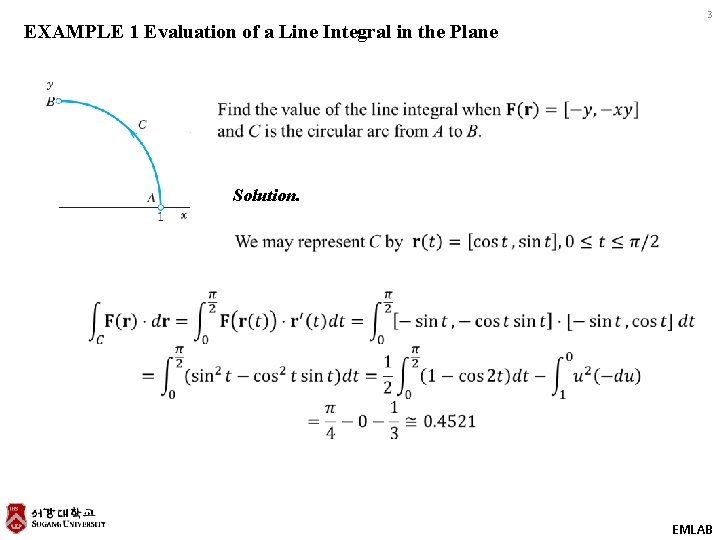
3 EXAMPLE 1 Evaluation of a Line Integral in the Plane Solution. EMLAB

4 THEOREM 1 Direction-Preserving Parametric Transformations Any representations of C that give the same positive direction on C also yield the same value of the line integral PROOF EMLAB

5 Motivation of the Line Integral : Work Done by a Force The sum of these n works is Other Forms of Line Integrals EMLAB

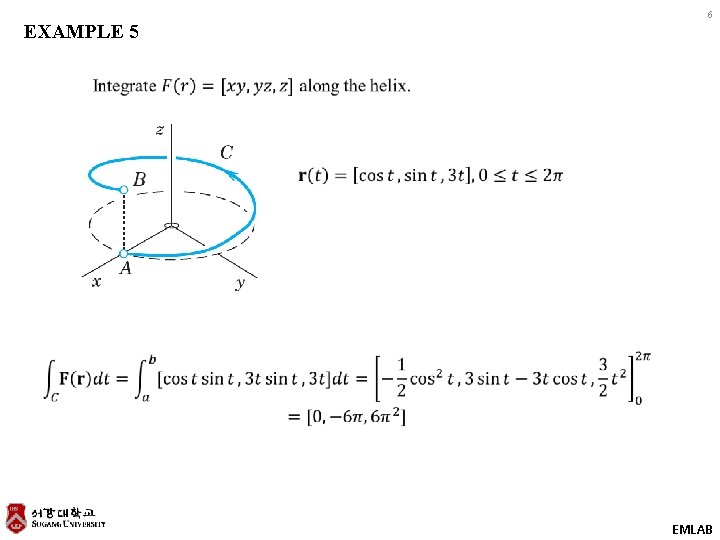
6 EXAMPLE 5 EMLAB

7 THEOREM 2 Path Dependence The line integral generally depends not only on F and on the endpoints A and B of the path, but also on the path itself along which the integral is taken. EMLAB

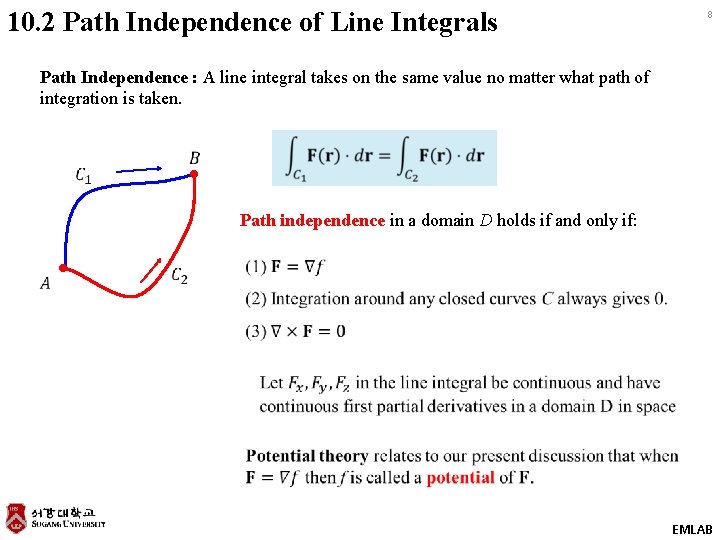
10. 2 Path Independence of Line Integrals 8 Path Independence : A line integral takes on the same value no matter what path of integration is taken. Path independence in a domain D holds if and only if: EMLAB

9 Conditions for path independence EMLAB

10 Test for exactness EMLAB

11 EXAMPLE 2 Path Independence. Determination of a Potential Evaluate the integral from A(0, 1, 2) to B(1, -1, 7) by showing that F has a potential. Solution. If F has a potential f, we should have EMLAB

EXAMPLE 3 Exactness and Independence of Path. Determination of a Potential 12 Show that the differential form under the integral sign of EMLAB

13 EXAMPLE 4 On the Assumption of Simple Connectedness in the proof EMLAB

14 EMLAB

10. 3 Calculus Review: Double Integrals. 15 Fig. 227. Subdivision of a region R EMLAB

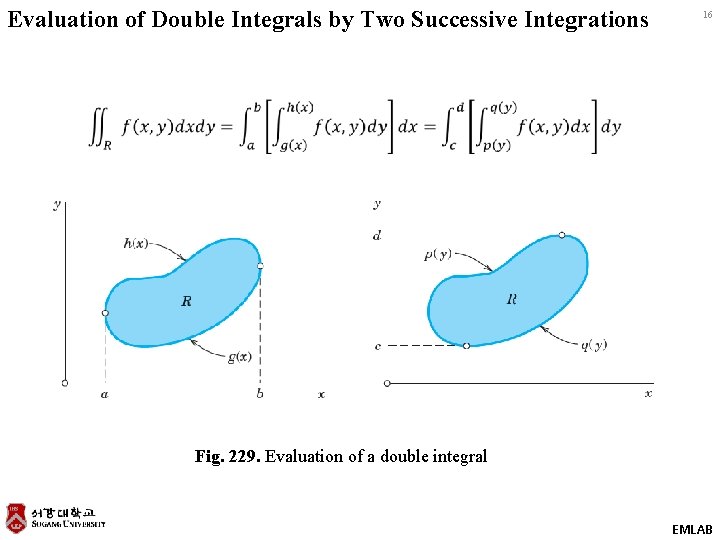
Evaluation of Double Integrals by Two Successive Integrations 16 Fig. 229. Evaluation of a double integral EMLAB

Applications of Double Integrals 17 Area A of a region R in the xy-plane is Then the total mass M in R is the center of gravity of the mass in R EMLAB

18 the moments of inertia the polar moment of inertia EMLAB

Change of Variables in Double Integrals. Jacobian 19 change of the variables of integration in integrals. The formula for a change of variables in double integrals from x, y to u, v is EMLAB

EXAMPLE 1 Change of Variables in a Double Integral 20 Evaluate the following double integral over the square R in Fig. 232. Region R in Example 1 EMLAB

21 EMLAB

EXAMPLE 2 Double Integrals in Polar Coordinates. Center of Gravity. Moments of Inertia 22 The center of gravity has the coordinates For reasons of symmetry. EMLAB

23 The moments of inertia are For reasons of symmetry. EMLAB

10. 4 Green’s Theorem in the Plane 24 Green’s Theorem in the Plane (Transformation between Double Integrals and Line Integrals) Here we integrate along the entire boundary C of R in such a sense that R is on the left as we advance in the direction of integration EMLAB

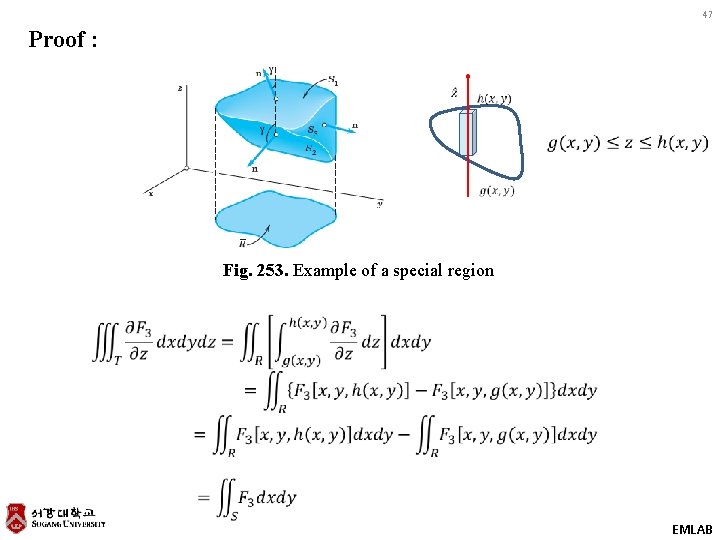
25 PROOF We prove Green’s theorem in the plane, first for a special region R that can be represented in both forms Fig. 235. Example of a special region EMLAB

26 EMLAB

27 Fig. 237. Proof of Green’s theorem Some Applications of Green’s Theorem EXAMPLE 2 Area of a Plane Region as a Line Integral Over the Boundary EMLAB

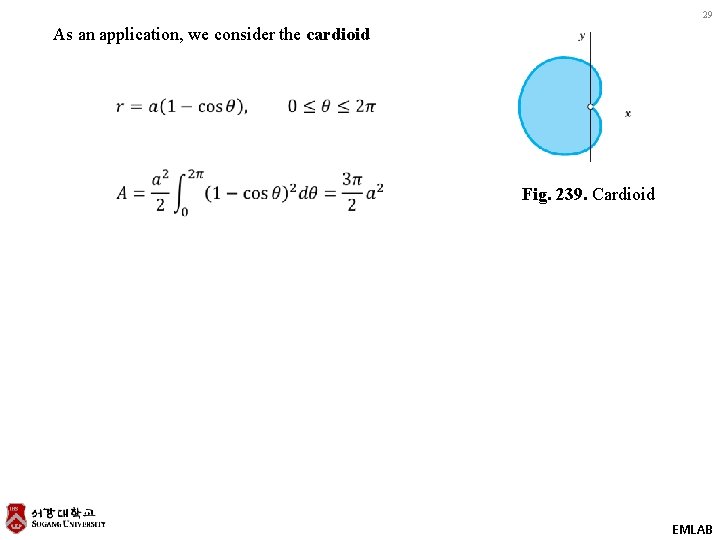
28 For an ellipse EXAMPLE 3 Area of a Plane Region in Polar Coordinates EMLAB

29 As an application, we consider the cardioid Fig. 239. Cardioid EMLAB

EXAMPLE 4 Transformation of a Double Integral of the Laplacian of a Function into a Line Integral of Its Normal Derivative 30 EMLAB
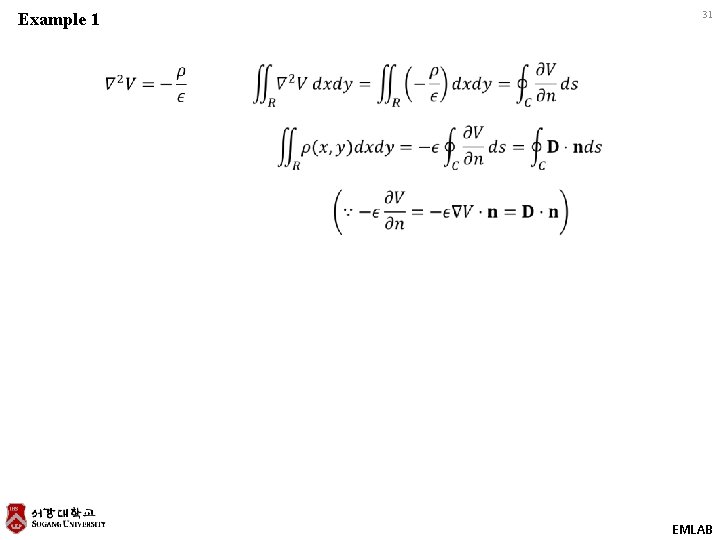
Example 1 31 EMLAB
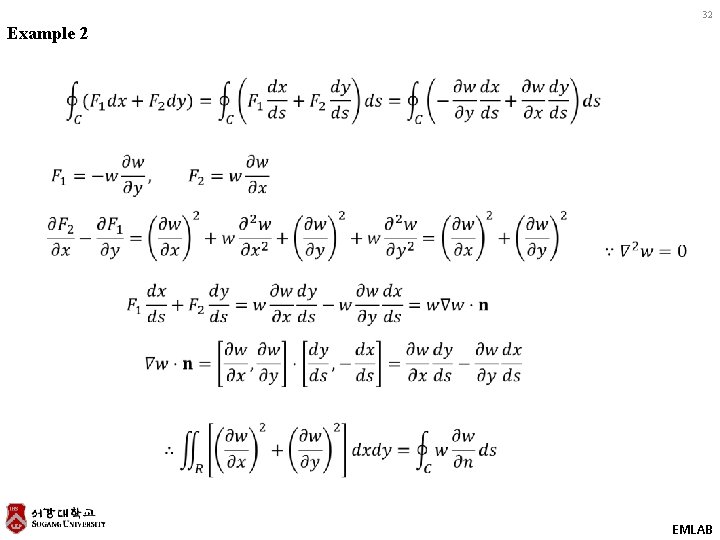
32 Example 2 EMLAB

10. 6 Surface Integrals 33 Representation of Surfaces Example For surfaces S in surface integrals, it will often be more practical to use a parametric representation. Surfaces are two-dimensional. Hence we need two parameters. Fig. 241. Parametric representations of a curve and a surface EMLAB

EXAMPLE 1 Parametric Representation of a Cylinder 34 Fig. 242. Parametric representation of a cylinder EMLAB

EXAMPLE 2 Parametric Representation of a Sphere 35 Fig. 243. Parametric representation of a cylinder of a sphere EXAMPLE 3 Parametric Representation of a Cone EMLAB

Tangent Plane and Surface Normal 36 Fig. 244. Tangent plane and normal vector EXAMPLE 4 Unit Normal Vector of a Sphere EMLAB

37 EXAMPLE 5 Unit Normal Vector of a cone EMLAB

10. 6 Surface Integrals 38 ; unit normal vector EMLAB

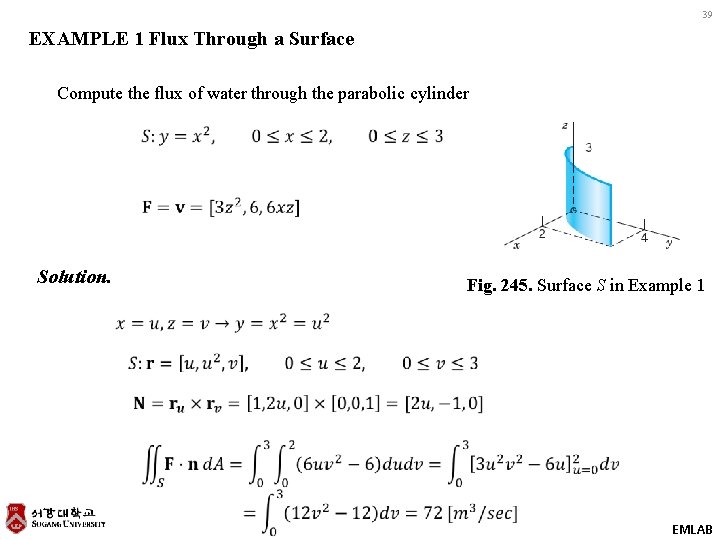
39 EXAMPLE 1 Flux Through a Surface Compute the flux of water through the parabolic cylinder Solution. Fig. 245. Surface S in Example 1 EMLAB

40 EXAMPLE 2 Surface Integral Solution. Fig. 246. Portion of a plane in Example 2 EMLAB

Surface Integrals Without Regard to Orientation 41 mean value theorem for surface integrals If R in the above integral is simply connected and G(r) is continuous in a domain containing R, then there is a point in R such that If G = 1, (6) gives the area A(S) of S, EMLAB

42 EXAMPLE 4 Area of a Sphere EMLAB

43 EXAMPLE 5 Torus Surface (Doughnut Surface): Representation and Area Fig. 249. Torus in Example 5 EMLAB

44 EMLAB

10. 7 Triple Integrals. Divergence Theorem of Gauss 45 EMLAB

Divergence Theorem of Gauss 46 (Transformation Between Triple and Surface Integrals) EMLAB

47 Proof : Fig. 253. Example of a special region EMLAB

EXAMPLE 1 Evaluation of a Surface Integral by the Divergence Theorem 48 Evaluate where S is the closed surface in Fig. 252 consisting of the cylinder Fig. 252. Surface S Solution. EMLAB

EXAMPLE 2 Verification of the Divergence Theorem 49 Evaluate Solution. (a) Volume integral (a) Surface integral EMLAB
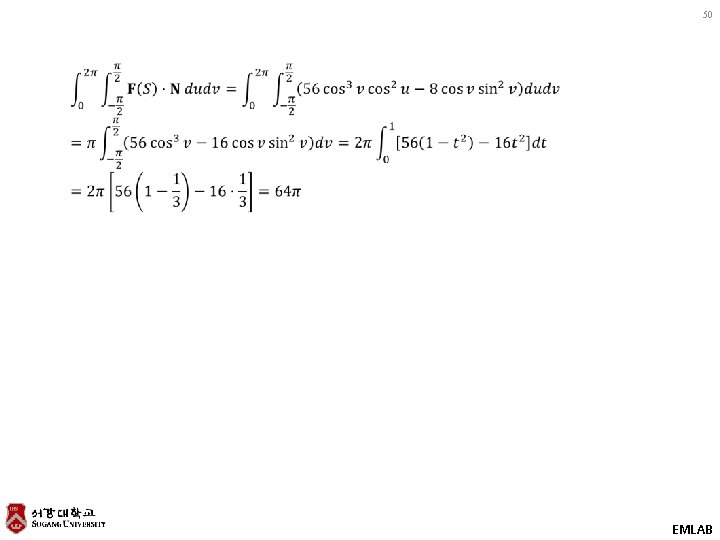
50 EMLAB

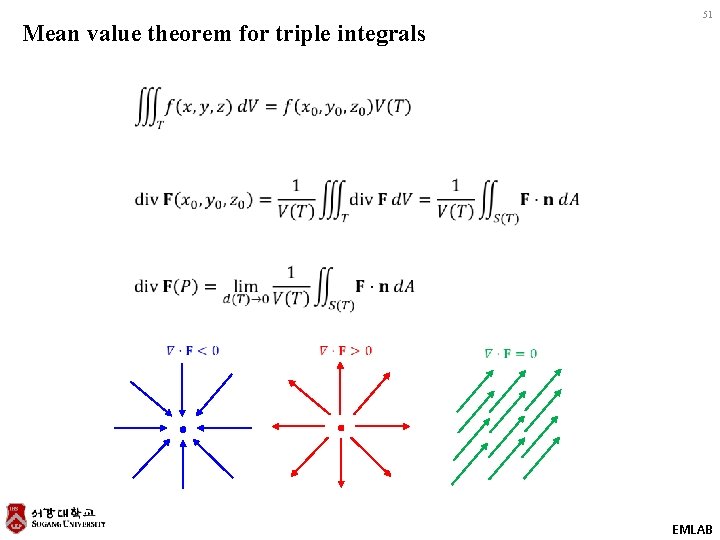
Mean value theorem for triple integrals 51 EMLAB

10. 8 Further Applications of the Divergence Theorem 52 EXAMPLE 4 Green’s Theorems Green’s first formula Green’s second formula EMLAB
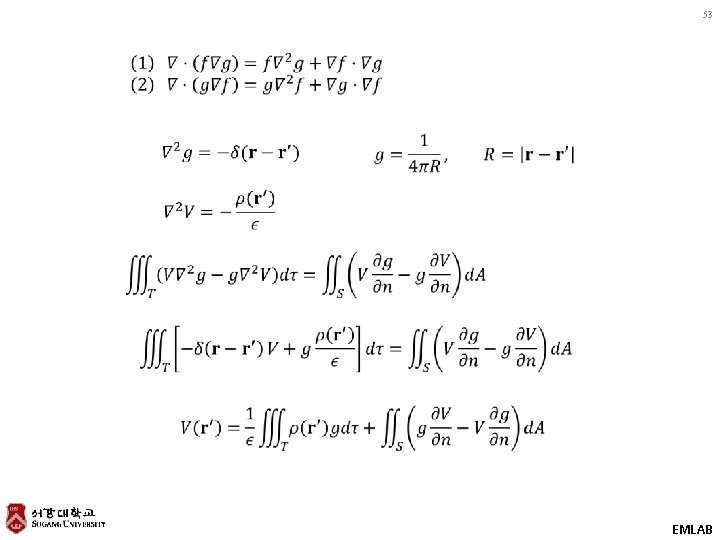
53 EMLAB

10. 9 Stokes’ Theorem 54 Fig. 254. Stokes’ theorem EMLAB

55 Fig. 256. Proof of Stokes’s theorem EMLAB
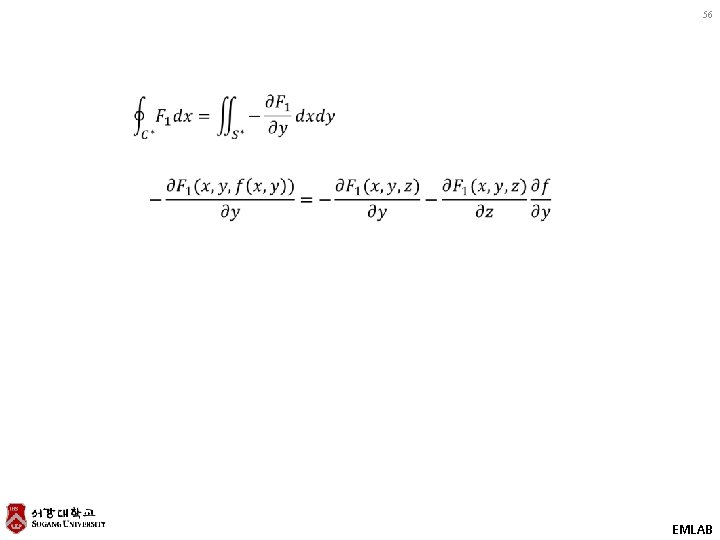
56 EMLAB

57 EXAMPLE 1 Verification of Stokes’s Theorem Evaluate a line integral along the perimeter of the paraboloid. Fig. 255. Surface S in Example 1 EMLAB
 Average rate of change with integrals
Average rate of change with integrals Second fundamental theorem of calculus
Second fundamental theorem of calculus Calculus examples
Calculus examples Gradient of scalar point function
Gradient of scalar point function Gradient operator
Gradient operator Fundamental theorem of vector calculus
Fundamental theorem of vector calculus Calculus history timeline
Calculus history timeline Intergral calculus
Intergral calculus How to solve linear ode
How to solve linear ode Integration calculus formula
Integration calculus formula Properties of vector
Properties of vector Vector unitario de un vector
Vector unitario de un vector Why is vector resolution the opposite of vector addition
Why is vector resolution the opposite of vector addition What is position vector
What is position vector Line integral of vector field
Line integral of vector field Displacement integral
Displacement integral Non integral citation
Non integral citation Integral and non integral citation
Integral and non integral citation Surface integrals of scalar functions
Surface integrals of scalar functions Non integral foreign operation meaning
Non integral foreign operation meaning Integral dx
Integral dx Calculus chapter 5
Calculus chapter 5 Stewart calculus chapter 11
Stewart calculus chapter 11 Calculus chapter 2 limits and continuity answers
Calculus chapter 2 limits and continuity answers Ap calculus chapter 5
Ap calculus chapter 5 Pre calculus chapter 1
Pre calculus chapter 1 Calculus chapter 3
Calculus chapter 3 Calculus chapter 12
Calculus chapter 12 Chapter p preparation for calculus
Chapter p preparation for calculus What is calculus
What is calculus Right triangle congruence theorems
Right triangle congruence theorems Trigonometry sides maze answer key
Trigonometry sides maze answer key Aa similarity theorem
Aa similarity theorem Parallelogram theorems
Parallelogram theorems Cyclic coordinate definition
Cyclic coordinate definition Cyclic coordinates and conservation theorems
Cyclic coordinates and conservation theorems Cpctc theorem
Cpctc theorem Parallel lines
Parallel lines List of theorems
List of theorems Triangle sum theorem formula
Triangle sum theorem formula Euclidean geometry grade 11 theorems
Euclidean geometry grade 11 theorems 4-4 the isosceles triangle theorems
4-4 the isosceles triangle theorems Circle theorems geogebra
Circle theorems geogebra Circle theorums
Circle theorums Tangent rules circle
Tangent rules circle Circle theorems gcse questions
Circle theorems gcse questions Parts of a circle
Parts of a circle Thevenin theorem
Thevenin theorem Exterior angle theorem worksheet
Exterior angle theorem worksheet 5-5 theorems about roots of polynomial equations
5-5 theorems about roots of polynomial equations Parallelogram is a kite
Parallelogram is a kite Kite theorems
Kite theorems M<5
M<5 5-3 theorems involving parallel lines
5-3 theorems involving parallel lines What is remainder theorem
What is remainder theorem Stokes theorem examples
Stokes theorem examples Electrical theorems
Electrical theorems Bond pricing theorems
Bond pricing theorems