ESSENTIAL CALCULUS CH 12 Multiple integrals In this




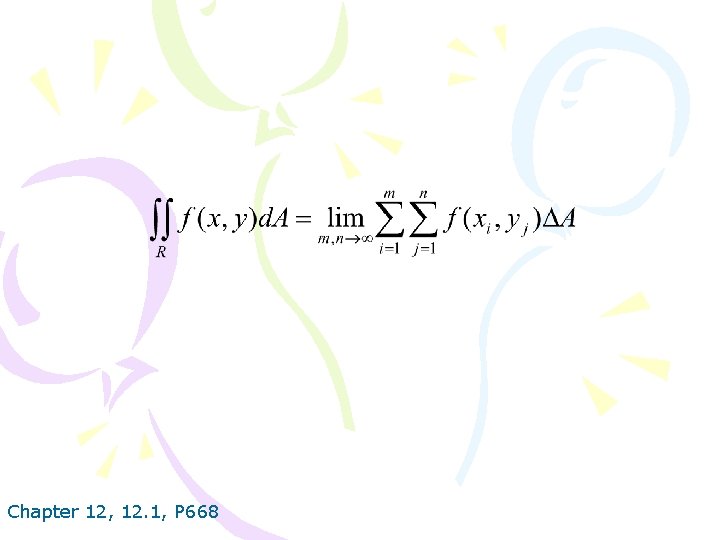
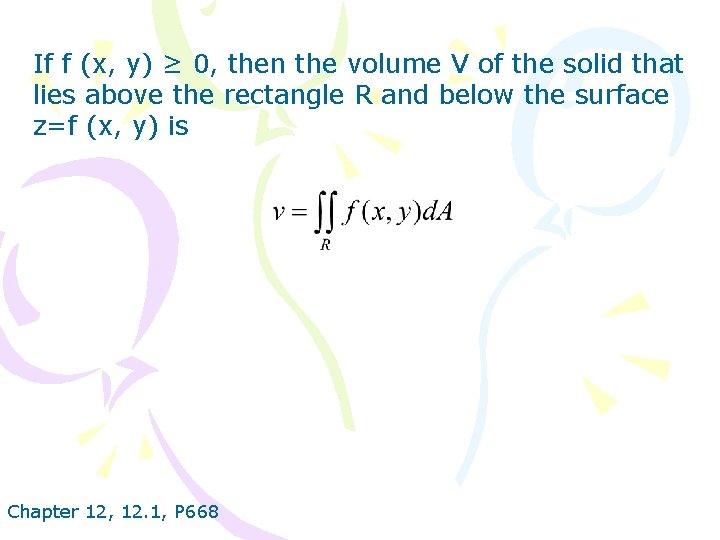
![MIDPOINT RULE FOR DOUBLE INTEGRALS where xi is the midpoint of [xi-1, xi] and MIDPOINT RULE FOR DOUBLE INTEGRALS where xi is the midpoint of [xi-1, xi] and](https://slidetodoc.com/presentation_image_h/2576218f11d5a804c893f00259634037/image-9.jpg)

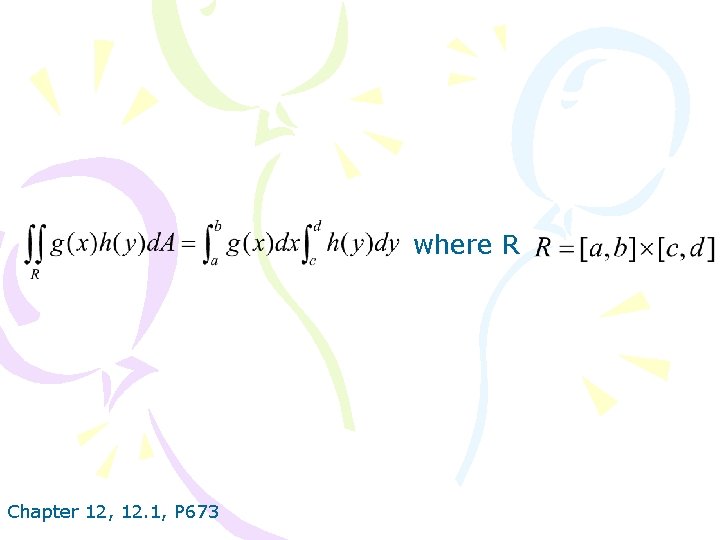

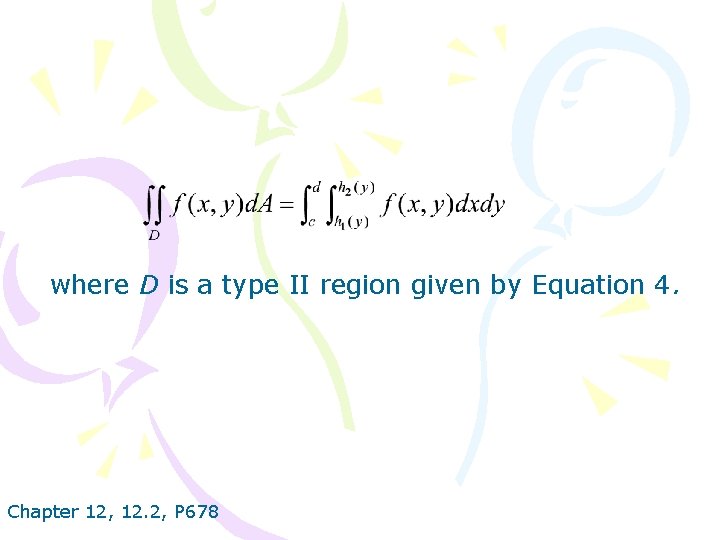

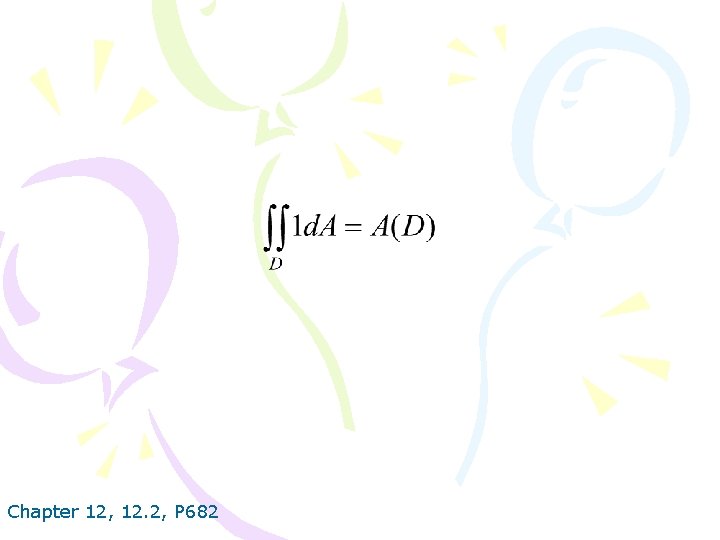
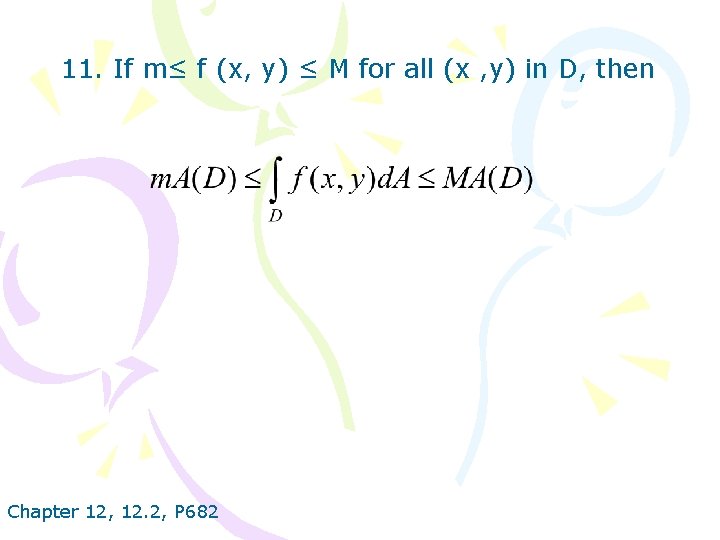






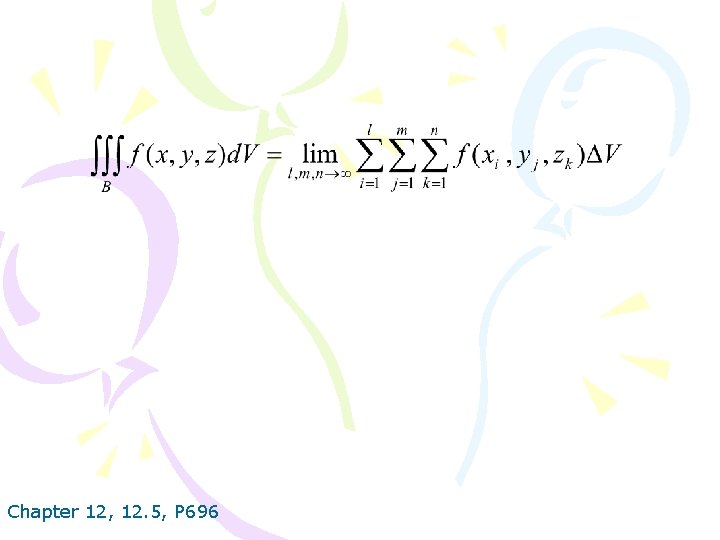




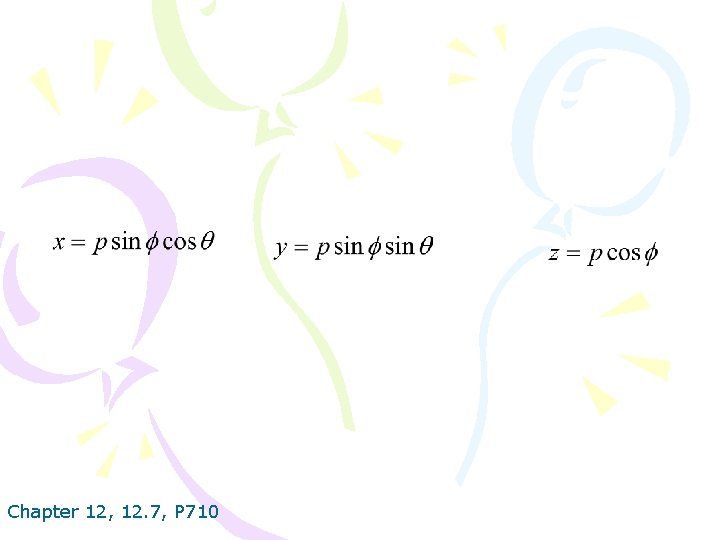






- Slides: 59

ESSENTIAL CALCULUS CH 12 Multiple integrals

In this Chapter: n 12. 1 Double Integrals over Rectangles n 12. 2 Double Integrals over General Regions n 12. 3 Double Integrals in Polar Coordinates n 12. 4 Applications of Double Integrals n 12. 5 Triple Integrals n 12. 6 Triple Integrals in Cylindrical Coordinates n 12. 7 Triple Integrals in Spherical Coordinates n 12. 8 Change of Variables in Multiple Integrals Review

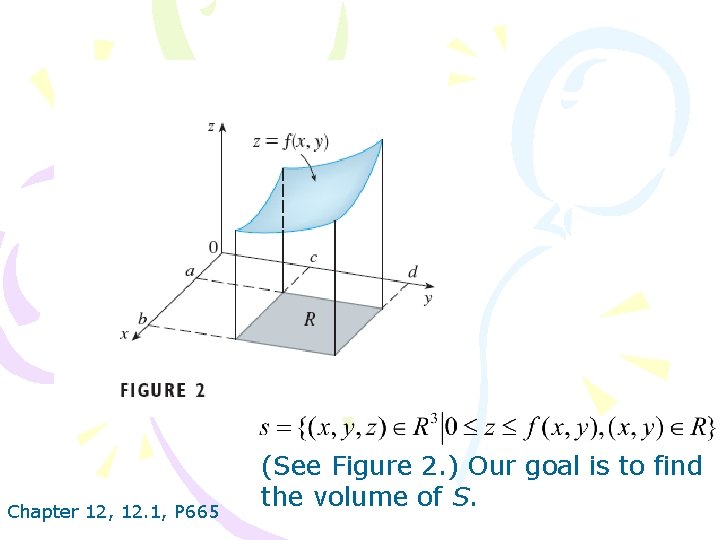
Chapter 12, 12. 1, P 665 (See Figure 2. ) Our goal is to find the volume of S.

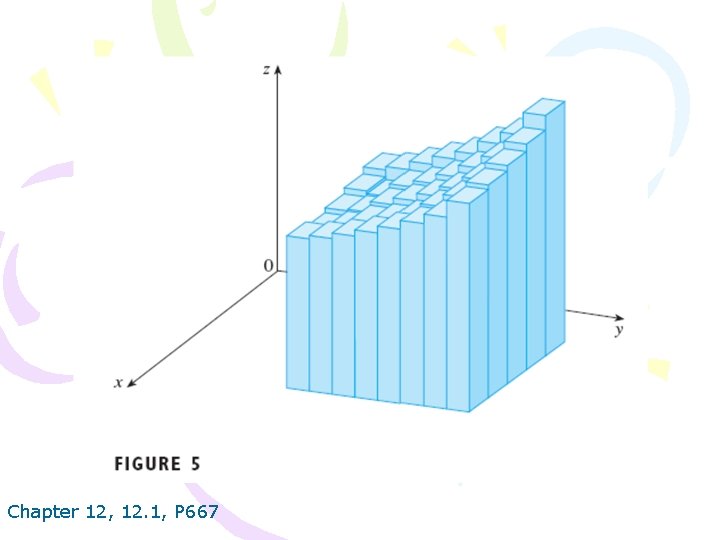
Chapter 12, 12. 1, P 667

Chapter 12, 12. 1, P 667

5. DEFINITION The double integral of f over the rectangle R is if this limit exists. Chapter 12, 12. 1, P 667
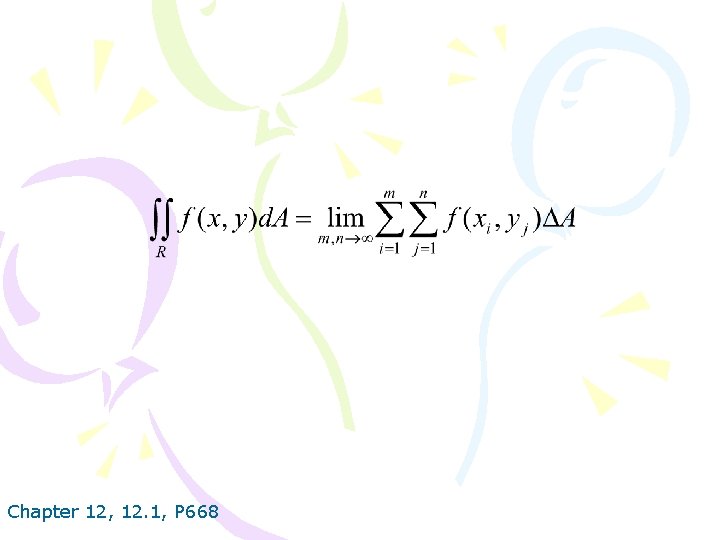
Chapter 12, 12. 1, P 668
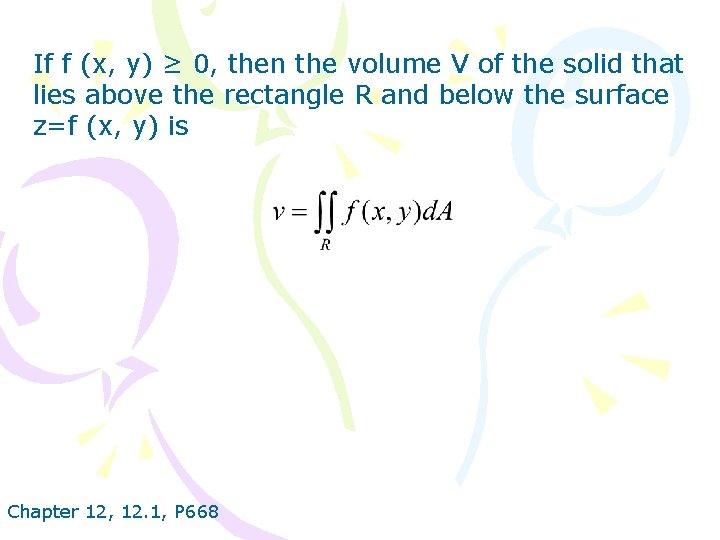
If f (x, y) ≥ 0, then the volume V of the solid that lies above the rectangle R and below the surface z=f (x, y) is Chapter 12, 12. 1, P 668
![MIDPOINT RULE FOR DOUBLE INTEGRALS where xi is the midpoint of xi1 xi and MIDPOINT RULE FOR DOUBLE INTEGRALS where xi is the midpoint of [xi-1, xi] and](https://slidetodoc.com/presentation_image_h/2576218f11d5a804c893f00259634037/image-9.jpg)
MIDPOINT RULE FOR DOUBLE INTEGRALS where xi is the midpoint of [xi-1, xi] and yj is the midpoint of [yj-1, yj ]. Chapter 12, 12. 1, P 669

10. FUBINI’S THEOREM If f is continuous on the rectangle R={(x, y} │a ≤ x≤ b, c ≤ y ≤d} , then More generally, this is true if we assume that f is bounded on R, is discontinuous only on a finite number of smooth curves, and the iterated integrals exist. Chapter 12, 12. 1, P 672
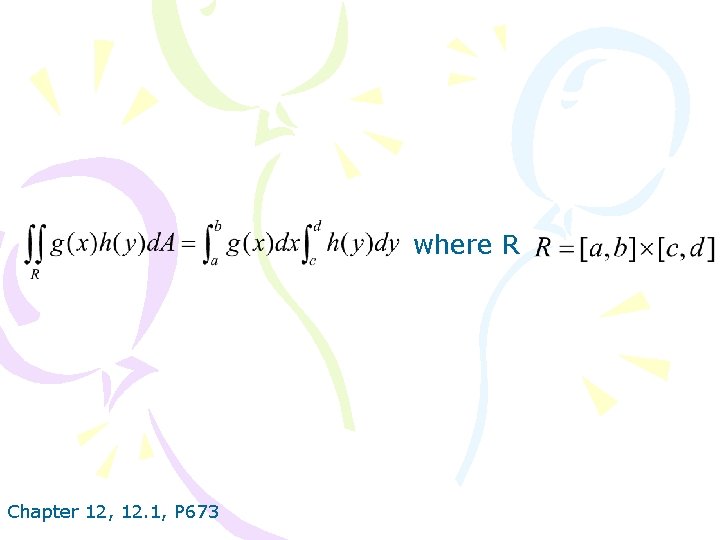
where R Chapter 12, 12. 1, P 673

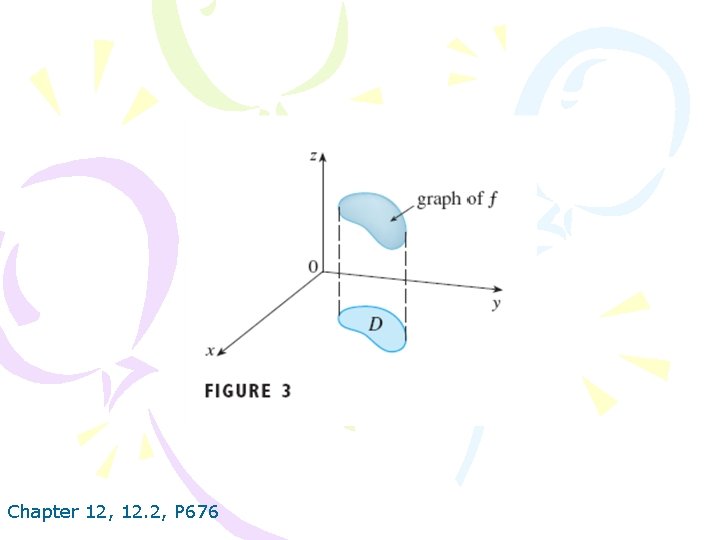
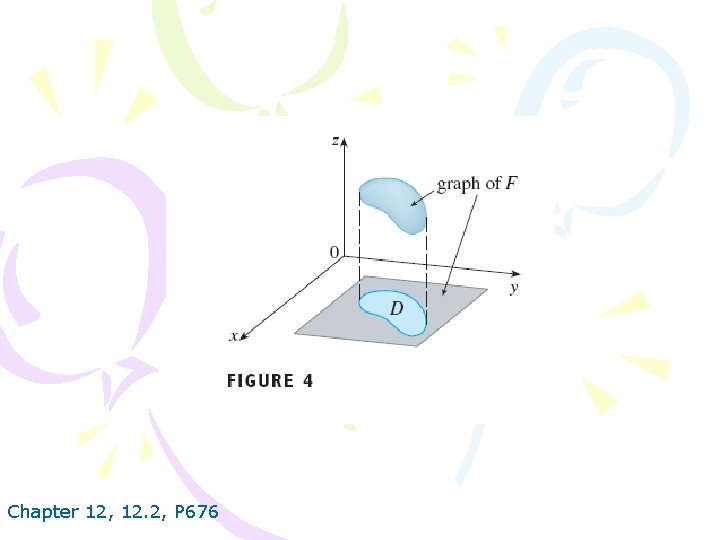
Chapter 12, 12. 2, P 676

Chapter 12, 12. 2, P 676

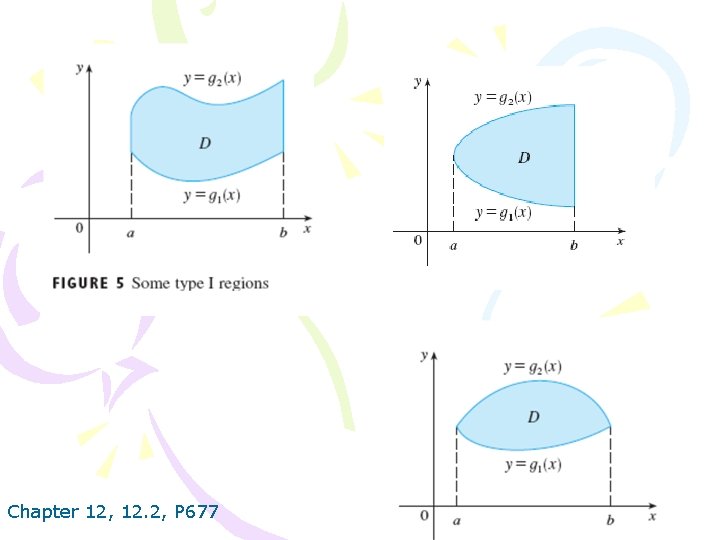
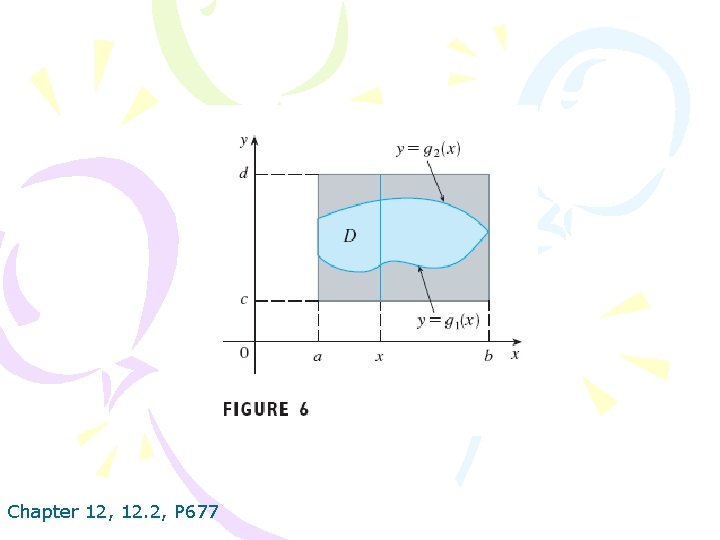
Chapter 12, 12. 2, P 677

Chapter 12, 12. 2, P 677

3. If f is continuous on a type I region D such that then Chapter 12, 12. 2, P 677

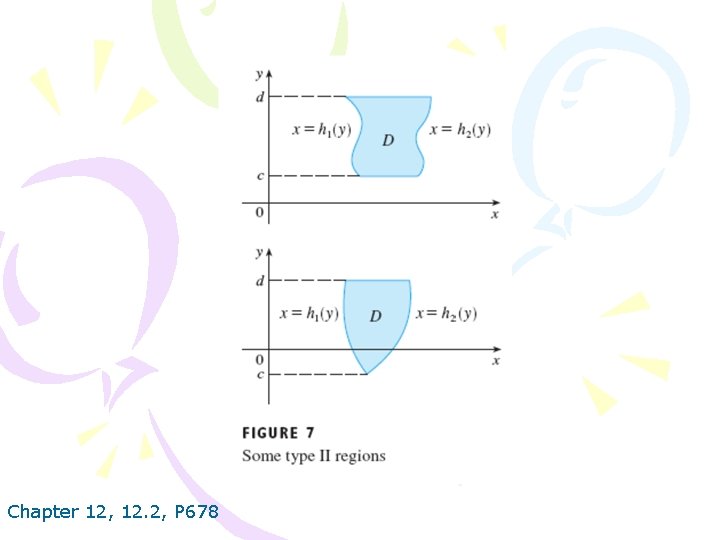
Chapter 12, 12. 2, P 678
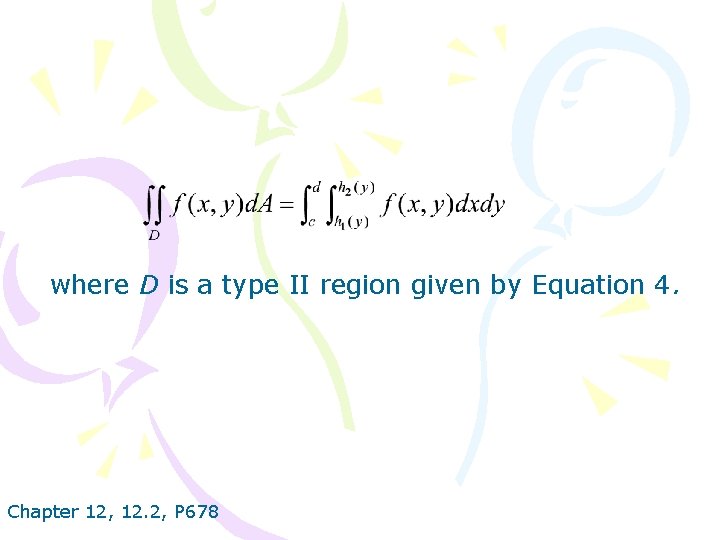
where D is a type II region given by Equation 4. Chapter 12, 12. 2, P 678

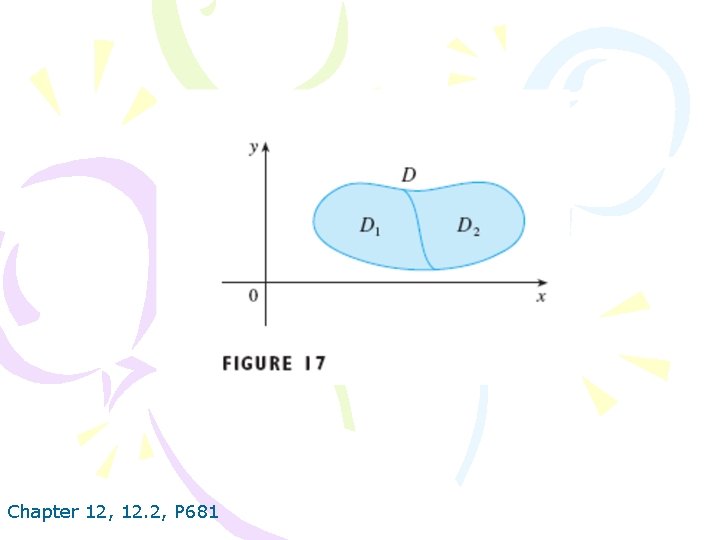
Chapter 12, 12. 2, P 681

6. 7. If f (x, y) ≥ g (x, y) for all (x, y) in D, then 8. If D=D 1 U D 2, where D 1 and D 2 don’t overlap except perhaps on their boundaries (see Figure 17), then Chapter 12, 12. 2, P 681
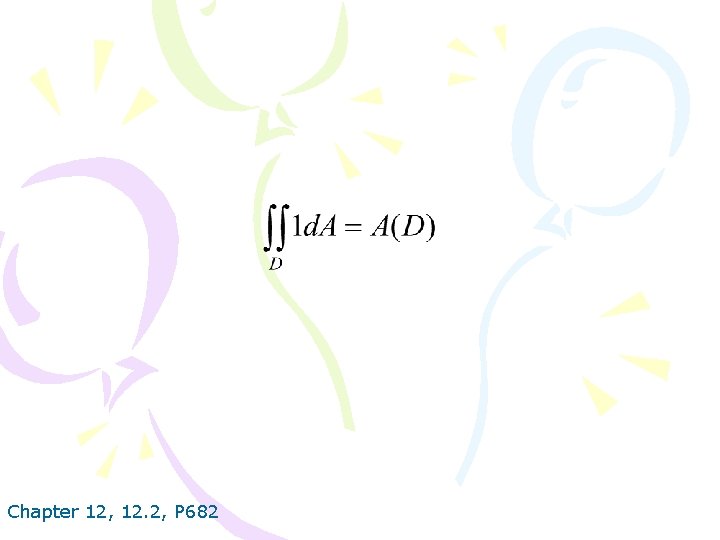
Chapter 12, 12. 2, P 682
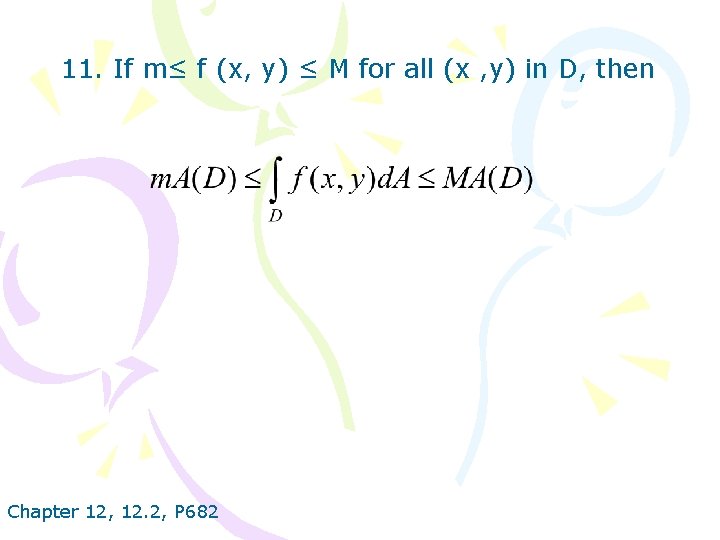
11. If m≤ f (x, y) ≤ M for all (x , y) in D, then Chapter 12, 12. 2, P 682

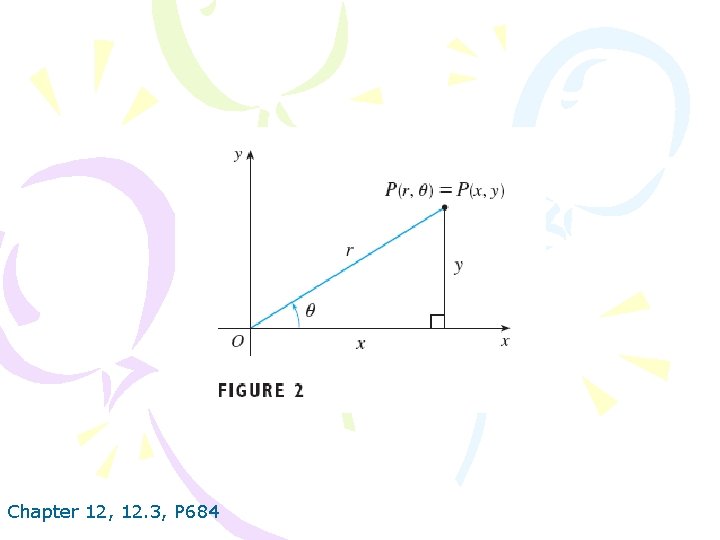
Chapter 12, 12. 3, P 684

Chapter 12, 12. 3, P 684

Chapter 12, 12. 3, P 684

r 2=x 2+y 2 Chapter 12, 12. 3, P 684 x=r cosθ y=r sinθ

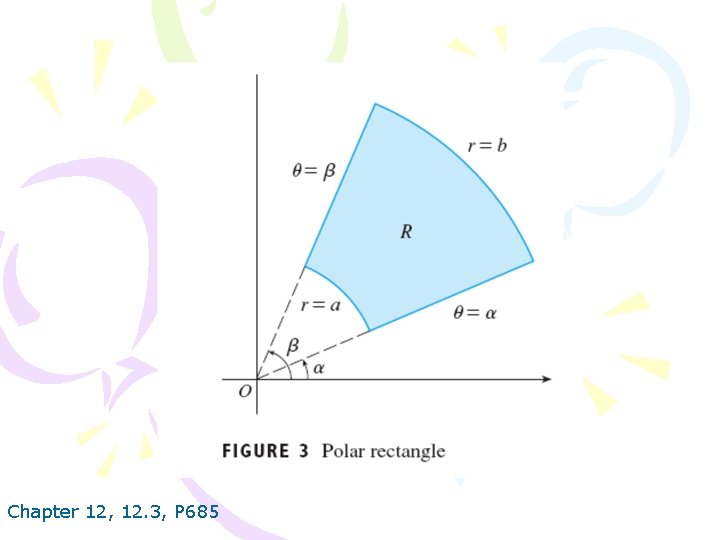
Chapter 12, 12. 3, P 685

2. CHANGE TO POLAR COORDINATES IN A DOUBLE INTEGRAL If f is continuous on a polar rectangle R given by 0≤a≤r≤b, a≤θ≤β, where 0≤β-α≤ 2 , then Chapter 12, 12. 3, P 686

3. If f is continuous on a polar region of the form then Chapter 12, 12. 3, P 687

3. DEFINITION The triple integral of f over the box B is if this limit exists. Chapter 12, 12. 5, P 696
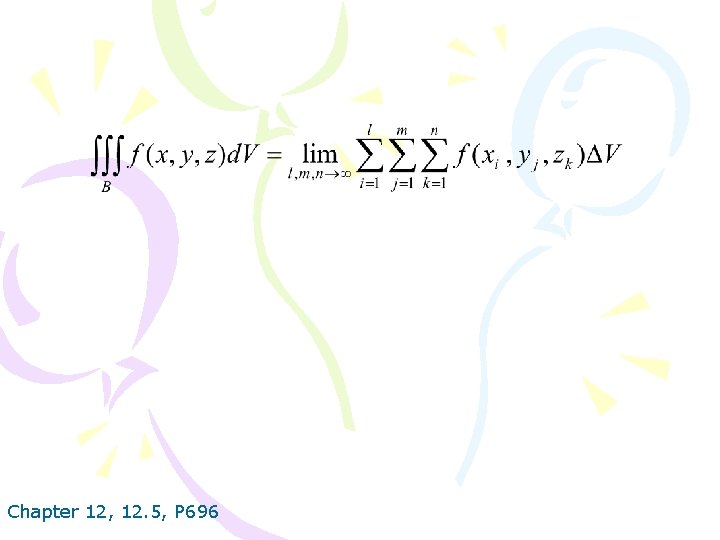
Chapter 12, 12. 5, P 696

4. FUBINI’S THEOREM FOR TRIPLE INTEGRALS If f is continuous on the rectangular box B=[a, b]╳ [c, d ]╳[r, s], then Chapter 12, 12. 5, P 696

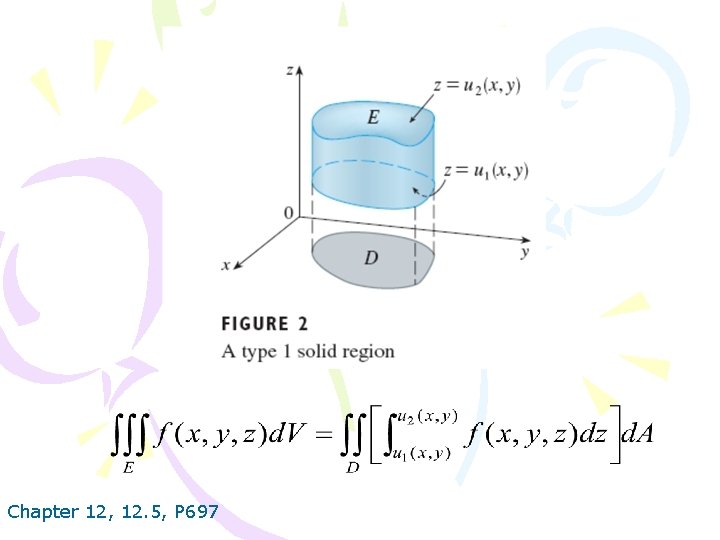
Chapter 12, 12. 5, P 697

Chapter 12, 12. 5, P 697

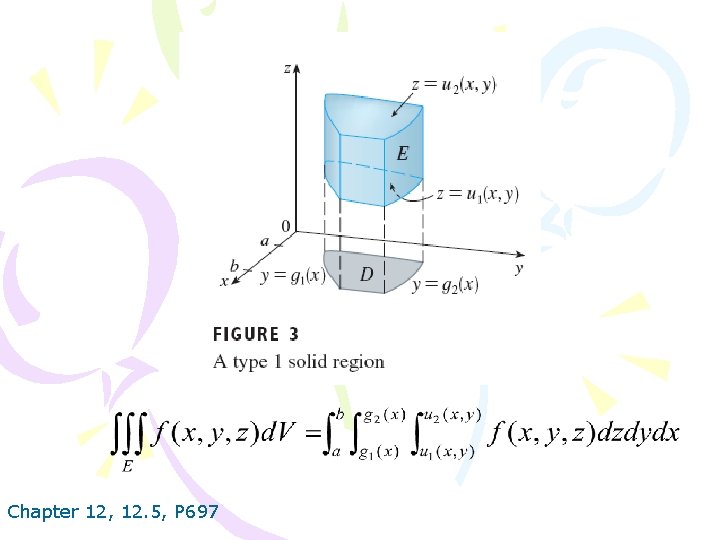
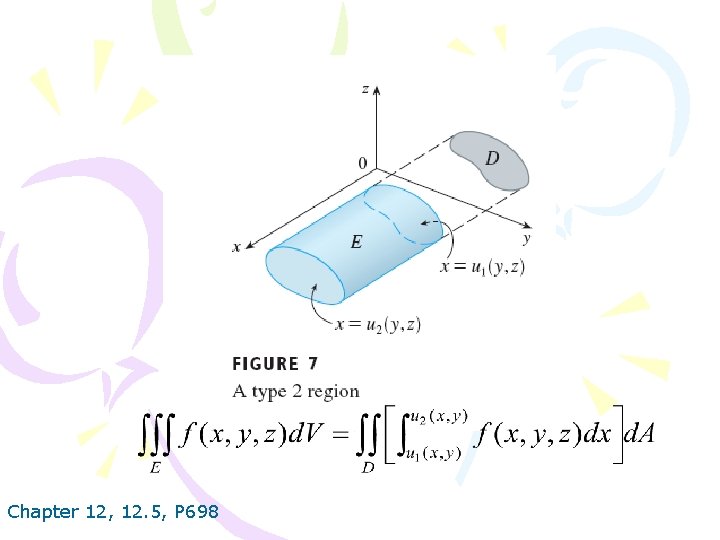
Chapter 12, 12. 5, P 698

Chapter 12, 12. 5, P 698

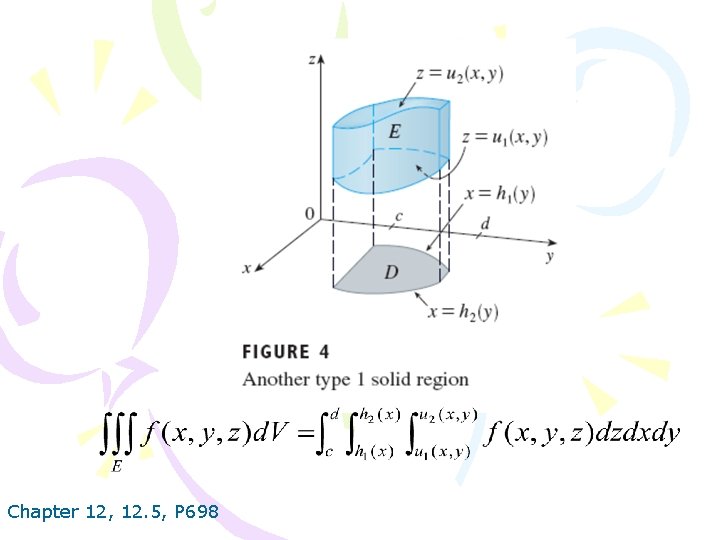
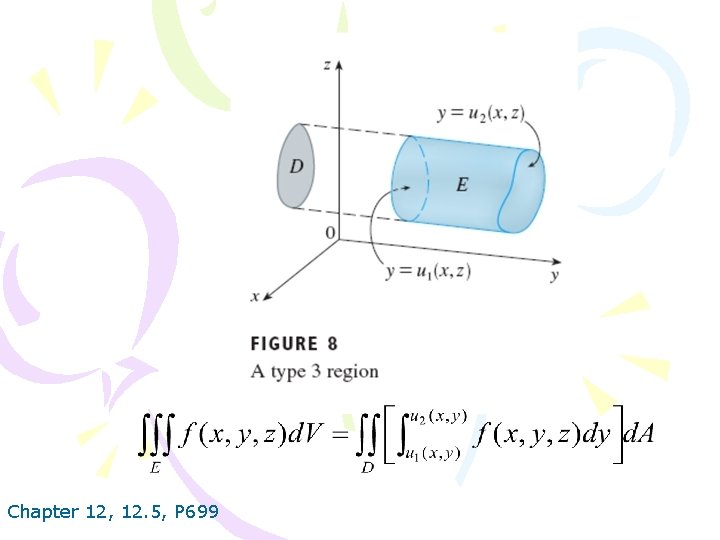
Chapter 12, 12. 5, P 699

Chapter 12, 12. 5, P 700

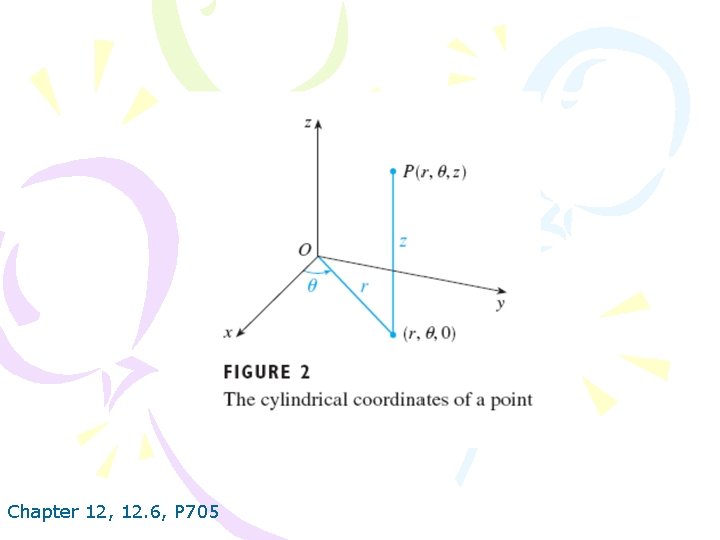
Chapter 12, 12. 6, P 705

To convert from cylindrical to rectangular coordinates, we use the equations 1 x=r cosθ y=r sinθ z=z whereas to convert from rectangular to cylindrical coordinates, we use 2. r 2=x 2+y 2 Chapter 12, 12. 6, P 705 tan θ= z=z

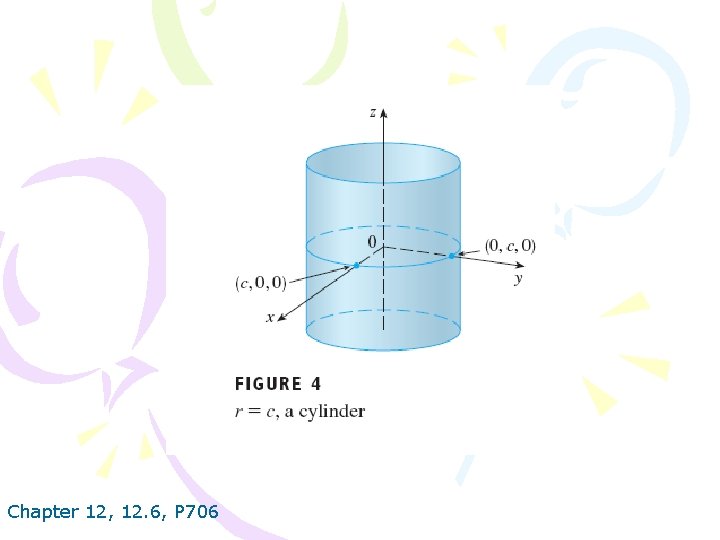
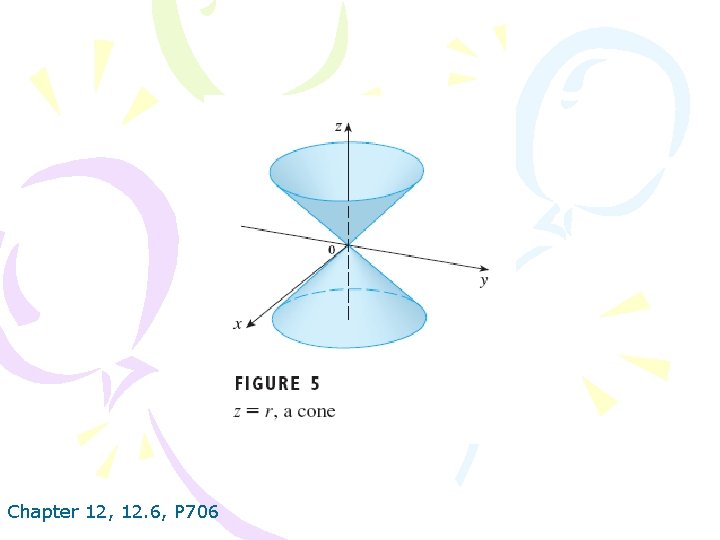
Chapter 12, 12. 6, P 706

Chapter 12, 12. 6, P 706

Chapter 12, 12. 6, P 706

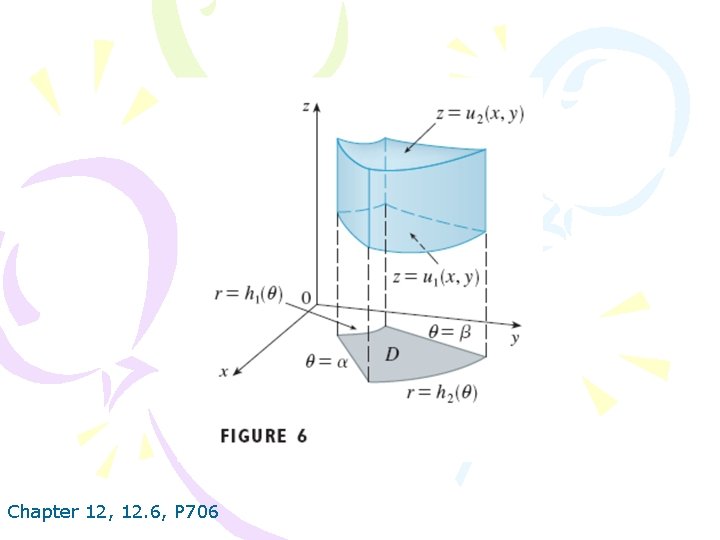
formula for triple integration in cylindrical coordinates. Chapter 12, 12. 6, P 707

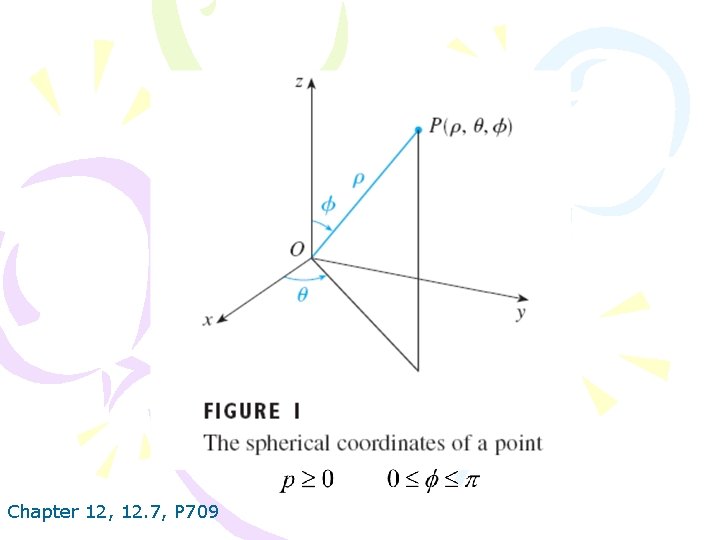
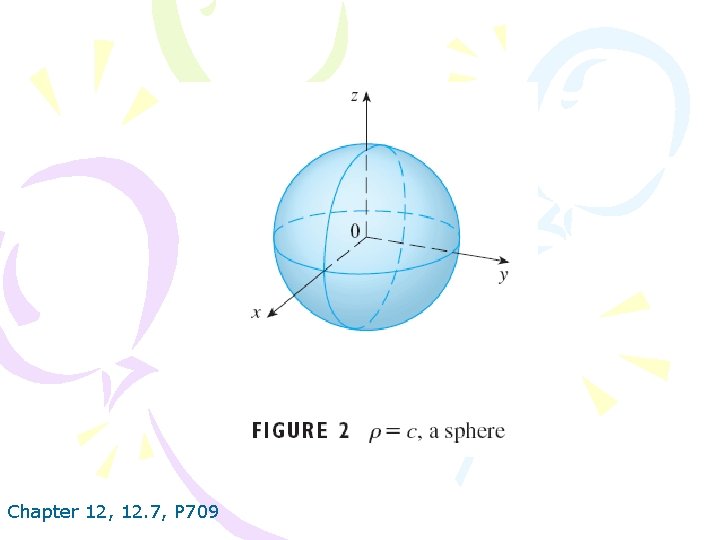
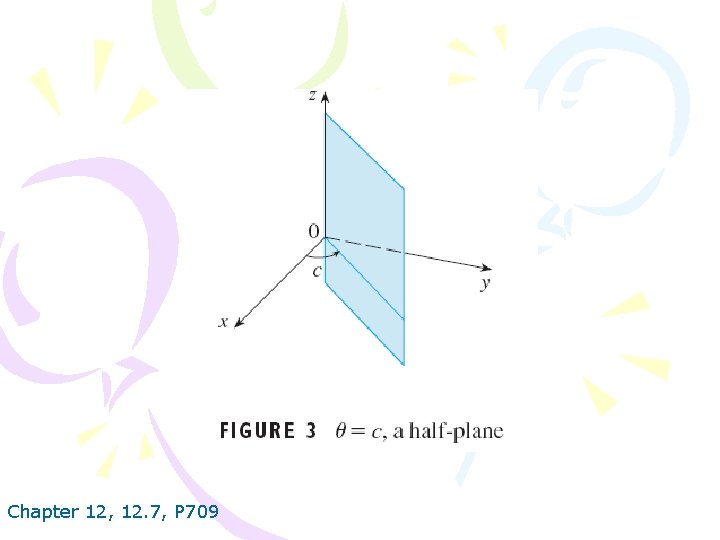
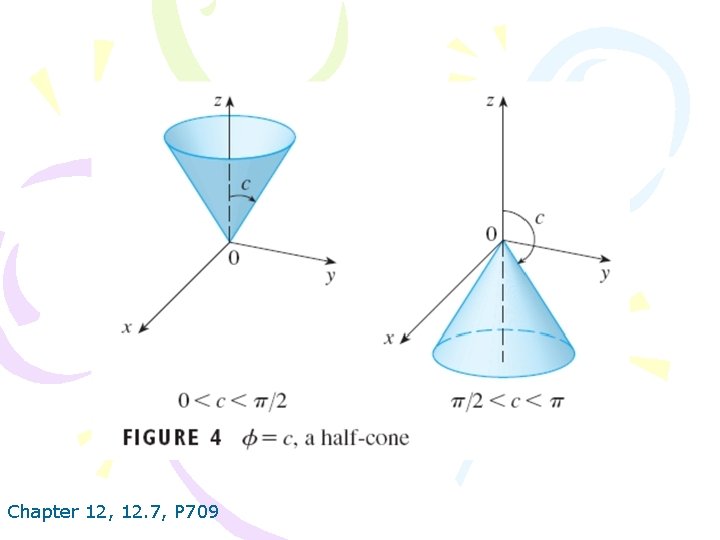
Chapter 12, 12. 7, P 709

Chapter 12, 12. 7, P 709

Chapter 12, 12. 7, P 709

Chapter 12, 12. 7, P 709

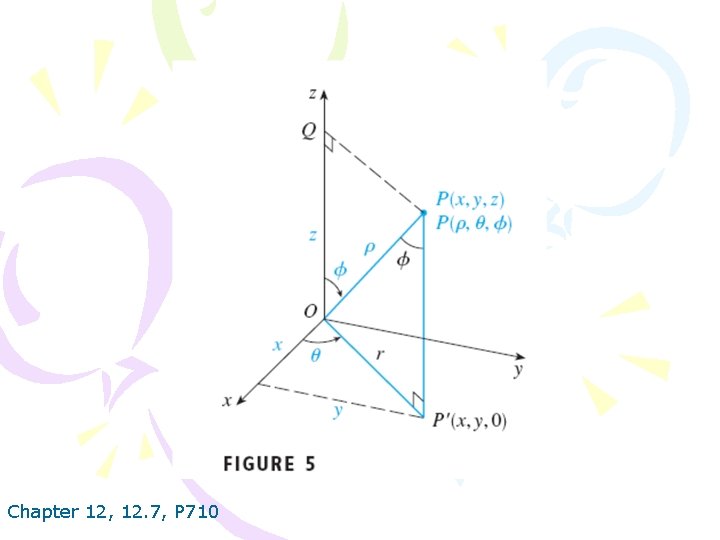
Chapter 12, 12. 7, P 710
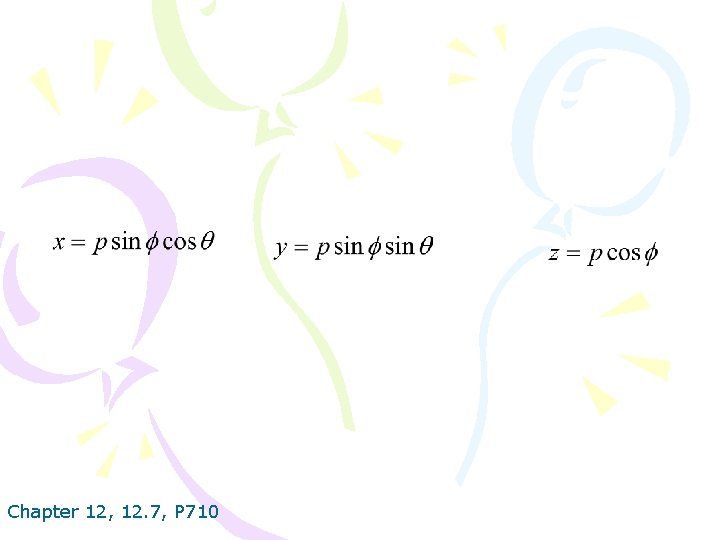
Chapter 12, 12. 7, P 710

Chapter 12, 12. 7, P 710

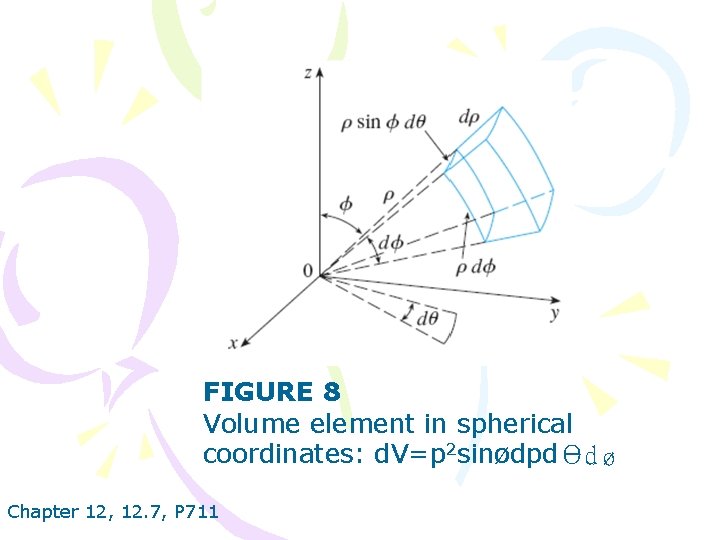
FIGURE 8 Volume element in spherical coordinates: d. V=p 2 sinødpdΘd ø Chapter 12, 12. 7, P 711

Formula for triple integration in spherical coordinates where E is a spherical wedge given by Chapter 12, 12. 7, P 711

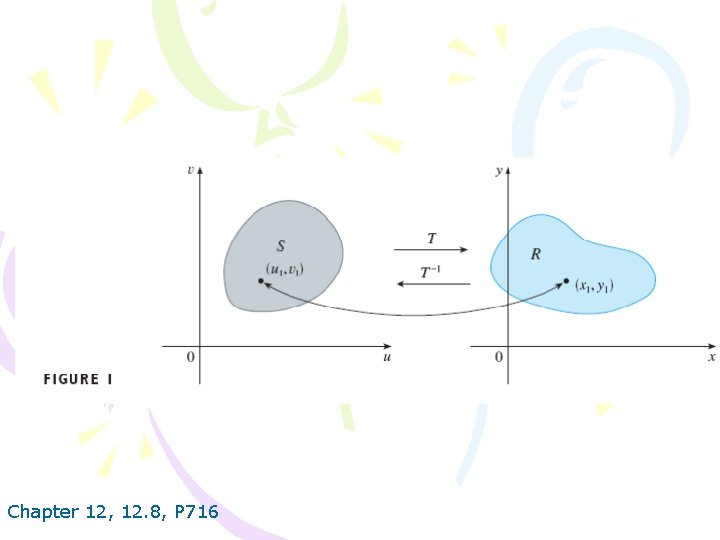
Chapter 12, 12. 8, P 716

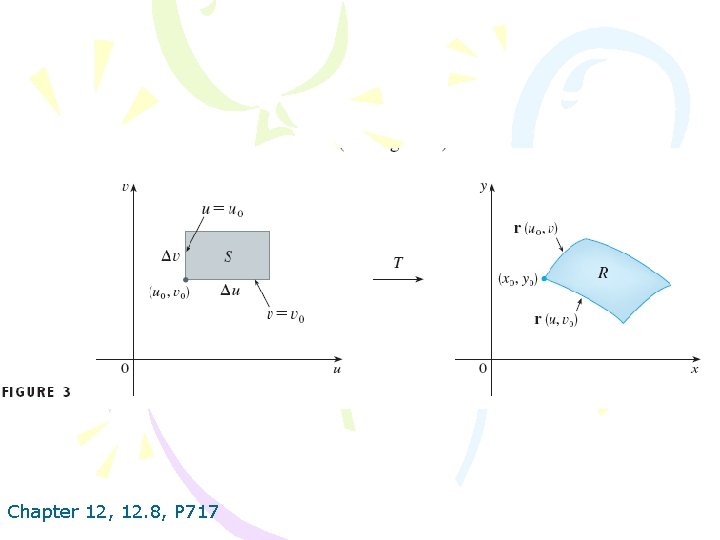
Chapter 12, 12. 8, P 717

7. DEFINITION The Jacobian of the transformation T given by x= g (u, v) and y= h (u, v) is Chapter 12, 12. 8, P 718

9. CHANGE OF VARIABLES IN A DOUBLE INTEGRAL Suppose that T is a C 1 transformation whose Jacobian is nonzero and that maps a region S in the uv-plane onto a region R in the xy-plane. Suppose that f is continuous on R and that R and S are type I or type II plane regions. Suppose also that T is one -to-one, except perhaps on the boundary of. S. Then Chapter 12, 12. 8, P 719

Let T be a transformation that maps a region S in uvw-space onto a region R in xyz-space by means of the equations x=g (u, v, w) y=h (u, v, w) z=k (u, v, w) The Jacobian of T is the following 3 X 3 determinant: 12. Chapter 12, 12. 8, P 721

13. Chapter 12, 12. 8, P 722