Sect 8 2 Cyclic Coordinates Conservation Theorems Definition

Sect. 8. 2: Cyclic Coordinates & Conservation Theorems • Definition of the Hamiltonian: (sum on i) H(q, p, t) qipi – L(q, q, t) (1) • A cyclic coordinate qi one which doesn’t appear in the Lagrangian L. Lagrange Eqtns pi (∂L/∂qi) = 0 pi (∂L/∂qi) = constant. The momentum conjugate to a cyclic coordinate qi is conserved. • Hamilton’s Eqtns get the same result. qi is cyclic From (1) qi doesn’t appear in H either. Hamilton’s Eqtn pi = - (∂H/∂qi) = 0 pi = constant. The momentum conjugate to a cyclic coord qi is conserved.

All momentum conservation theorems from Ch. 2 hold also in the Hamiltonian formalism. In Sect. 2. 6, merely replace L with H & all else carries over directly! • This statement includes the connections between the invariance or symmetry properties of the system & the conserved generalized momenta. § If the system is invariant (symmetrical) under uniform translation A Linear momentum is conserved. § System is invariant (symmetrical) under uniform rotation An Angular momentum is conserved.

• What about energy conservation? For H = H(q, p, t) (d. H/dt) ( H/ qi)qi + ( H/ pi)pi + ( H/ t) Hamilton’s Eqtns: qi = ( H/ pi), pi = - ( H/ qi) (d. H/dt) = ( H/ t) (a) In the derivation of Hamilton’s Eqtns, we also showed: ( H/ t) = - ( L/ t) (b) (a) & (b) together: (d. H/dt) = - ( L/ t) If L doesn’t depend explicitly on the time ( L/ t) = 0 neither does H: (d. H/dt) = 0 H = constant (conserved)

• Does H = constant (conserved) mean that energy is conserved? Not necessarily! • As in our discussion of the energy function h in Ch. 2, (Sect. 2. 7) the questions 1) Whether H = the total energy E & 2) Whether H is conserved are 2 separate questions!

Our discussion in Ch. 2 about the energy function h, also holds for the Hamiltonian H = qjpj - L • Special cases: a. ) The transformation equations from Cartesian to Generalized Coordinates are time independent b. ) The potential V is velocity independent. Only if a. ) & b. ) are BOTH satisfied is it true that: H = T + V = E Total Mechanical Energy • Under these conditions, if V is time independent, (∂L/∂t) = (d. H/dt) = 0 H = E = constant (conserved)

• Summary: Different Conditions: The Hamiltonian: H = qjpj - L ALWAYS: (d. H/dt) = - (∂L/∂t) SOMETIMES: V does not depend on t (d. H/dt) = 0 & H = constant (conserved) USUALLY: H = T + V = E Total Mechanical Energy Conservation Theorem for Mechanical Energy: If H = E AND it does not depend on t, E is conserved!

• Clearly, the conditions for conservation of the Hamiltonian H are DISTINCT from those which make it the total mechanical energy E. We can have conditions in which: 1. H is conserved & = E 2. H is not conserved & = E 3. H is conserved & E 4. H is not conserved & E The most common case in classical (& quantum) mechanics is case 1.

• Stated another way, there are two questions: 1. Does the Hamiltonian H = E for the system? 2. Is the mechanical energy E conserved for the system? • These are 2 aspects of the problem & are DIFFERENT questions! – We may have cases where H E, but E is conserved. – For example: A conservative system, using generalized coordinates which are in motion with respect to fixed rectangular axes: The transformation equations will contain the time T will NOT be a homogeneous, quadratic function of the generalized velocities! H E, However, because the system is conservative, E is conserved! (This is a physical fact about the system, independent of coordinate choices!).

• Note: L is independent of the choice of generalized coordinates. However, H depends on this choice! That is, for one choice of the qi, H may be conserved & for another it may not! • Example: Consider the 1 d system in the figure: A point mass m is attached to an ideal spring, constant k. Other end of the spring is fixed on a massless cart moving (by external means) to the right at constant speed v 0.

• Choose the origin so the cart is there at t = 0. Lagrangian: L(x, x) = T – V = (½)mx 2 - (½)k(x – v 0 t)2 Lagrange’s Equation: mx = -k(x – v 0 t) • Hamiltonian? • x is the Cartesian coordinate of the mass, V doesn’t involve velocity x H = total energy of the system: H = H(x, p, t) = E = T + V = p 2(2 m)-1 + (½)k(x – v 0 t)2 However, H = H(t) (d. H/dt) 0 H constant H is NOT conserved, but it IS the total energy!

• Another way to solve this: Change coordinates from x to x´ = x – v 0 t The Lagrangian: L(x´, x´) = (½)m(x´+ v 0)2 - (½)k(x´)2 = (½)m(x´)2 + mx´v 0 + (½)m(v 0)2 - (½)k(x´)2 mx´ = -kx´ • The Hamiltonian? • There is a term in L (mx´v 0) which is linear in x´. Corresponds to the qa term in the general formalism we’ve discussed. Here, a = mv 0. Using that formalism (or otherwise) the Hamiltonian: H = H(x´, p´) = (p´- mv 0)2(2 m)-1 + (½)k(x´)2 – (½)m(v 0)2 Now, H H(t) (d. H/dt) = 0 H = constant H IS conserved, but it IS NOT the total energy! (It is the energy of MOTION of m relative to the moving cart)

• SUMMARY: 1 Problem, 2 Hamiltonians! Different in magnitude, t dependence, & functional behavior! 1. H = H(x, p, t) = E = T + V = p 2(2 m)-1 + (½)k(x – v 0 t)2 H = H(t) (d. H/dt) 0 H constant H is NOT conserved, but it IS the total energy! 2. H = H(x´, p´) = (p´- mv 0)2(2 m)-1 + (½)k(x´)2 - (½)mx´(v 0)2 H H(t) (d. H/dt) = 0 H = constant H IS conserved, but it IS NOT the total energy! (It is the relative energy of MOTION of m with respect to the cart) • Both Hamiltonians obviously lead to the SAME equation of motion for the particle!

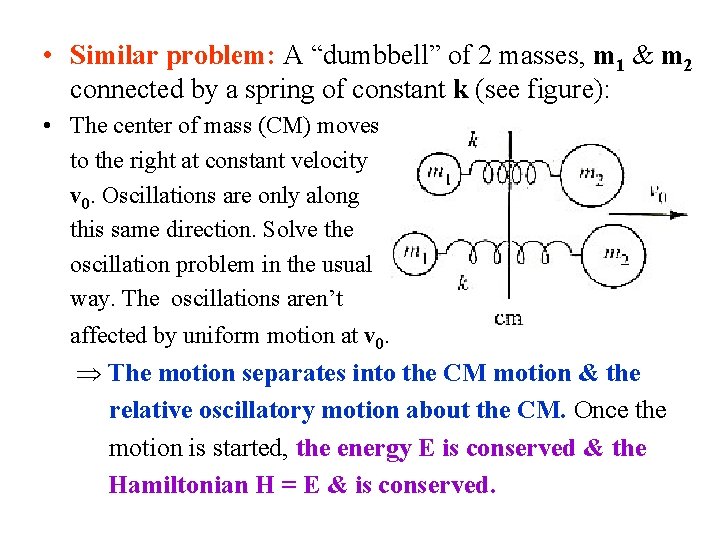
• Similar problem: A “dumbbell” of 2 masses, m 1 & m 2 connected by a spring of constant k (see figure): • The center of mass (CM) moves to the right at constant velocity v 0. Oscillations are only along this same direction. Solve the oscillation problem in the usual way. The oscillations aren’t affected by uniform motion at v 0. The motion separates into the CM motion & the relative oscillatory motion about the CM. Once the motion is started, the energy E is conserved & the Hamiltonian H = E & is conserved.

• A slightly different problem: The same “dumbbell” (see figure): m 2 moves to the right at constant velocity v 0. The CM & m 1 oscillate relative to m 2. This requires an external periodic force! Oscillations are affected by uniform motion at v 0. The motion doesn’t separate into the CM motion & the relative oscillatory motion. Because of the external oscillation force, the energy E is NOT conserved, the Hamiltonian H is NOT conserved & H E!