17 VECTOR CALCULUS VECTOR CALCULUS So far we





















































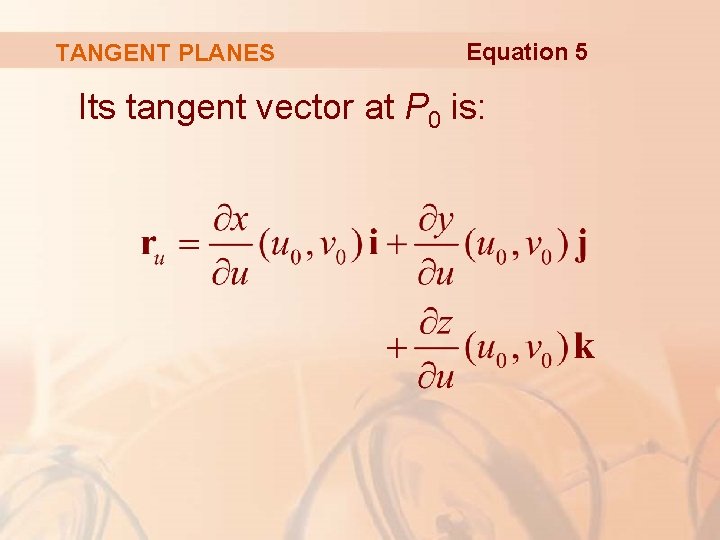





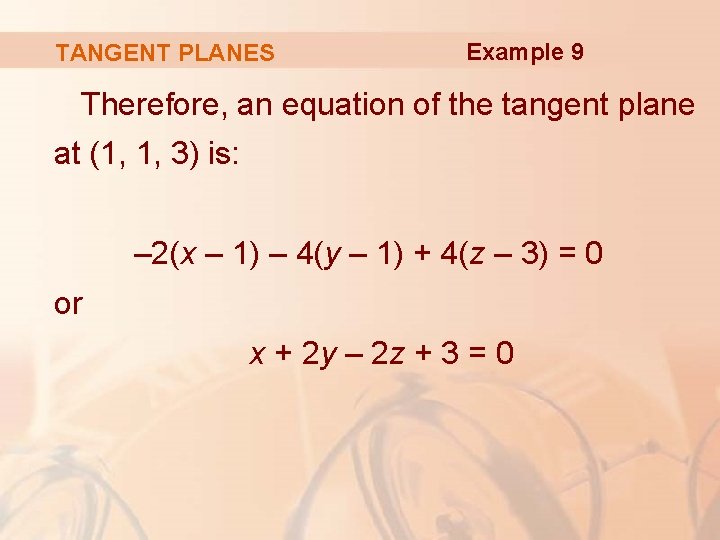





























- Slides: 107

17 VECTOR CALCULUS

VECTOR CALCULUS So far, we have considered special types of surfaces: § § Cylinders Quadric surfaces Graphs of functions of two variables Level surfaces of functions of three variables

VECTOR CALCULUS Here, we use vector functions to describe more general surfaces, called parametric surfaces, and compute their areas.

VECTOR CALCULUS Then, we take the general surface area formula and see how it applies to special surfaces.

VECTOR CALCULUS 17. 6 Parametric Surfaces and their Areas In this section, we will learn about: Various types of parametric surfaces and computing their areas using vector functions.

INTRODUCTION We describe a space curve by a vector function r(t) of a single parameter t. Similarly, we can describe a surface by a vector function r(u, v) of two parameters u and v.

INTRODUCTION Equation 1 We suppose that r(u, v) = x(u, v) i + y(u, v) j + z (u, v) k is a vector-valued function defined on a region D in the uv-plane.

INTRODUCTION So x, y, and z—the component functions of r—are functions of the two variables u and v with domain D.

PARAMETRIC SURFACE Equations 2 The set of all points (x, y, z) in such that x = x(u, v) z = z(u, v) y = y(u, v) and (u, v) varies throughout D, is called a parametric surface S. § Equations 2 are called parametric equations of S.

PARAMETRIC SURFACES Each choice of u and v gives a point on S. By making all choices, we get all of S.

PARAMETRIC SURFACES In other words, the surface S is traced out by the tip of the position vector r(u, v) as (u, v) moves throughout the region D.

PARAMETRIC SURFACES Example 1 Identify and sketch the surface with vector equation r(u, v) = 2 cos u i + v j + 2 sin u k § The parametric equations for this surface are: x = 2 cos u y=v z = 2 sin u

PARAMETRIC SURFACES Example 1 So, for any point (x, y, z) on the surface, we have: x 2 + z 2 = 4 cos 2 u + 4 sin 2 u =4 § This means that vertical cross-sections parallel to the xz-plane (that is, with y constant) are all circles with radius 2.

PARAMETRIC SURFACES Example 1 Since y = v and no restriction is placed on v, the surface is a circular cylinder with radius 2 whose axis is the y-axis.

PARAMETRIC SURFACES In Example 1, we placed no restrictions on the parameters u and v. So, we obtained the entire cylinder.

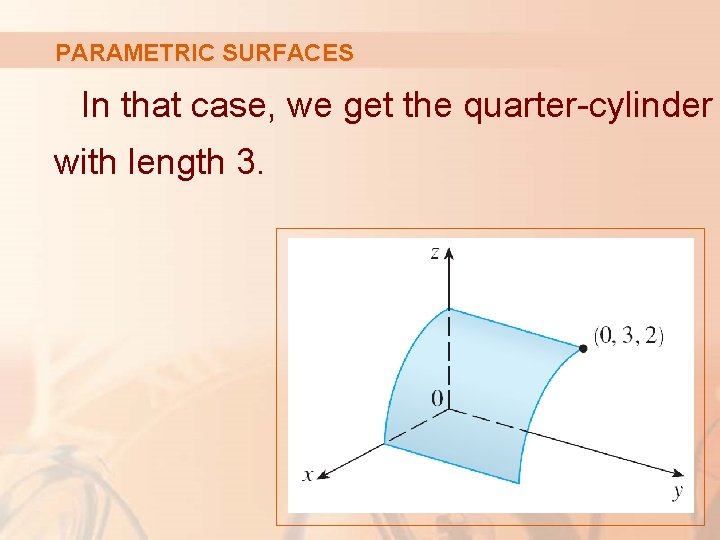
PARAMETRIC SURFACES If, for instance, we restrict u and v by writing the parameter domain as 0 ≤ u ≤ π/2 0≤v≤ 3 then x≥ 0 z≥ 0 0≤y≤ 3

PARAMETRIC SURFACES In that case, we get the quarter-cylinder with length 3.

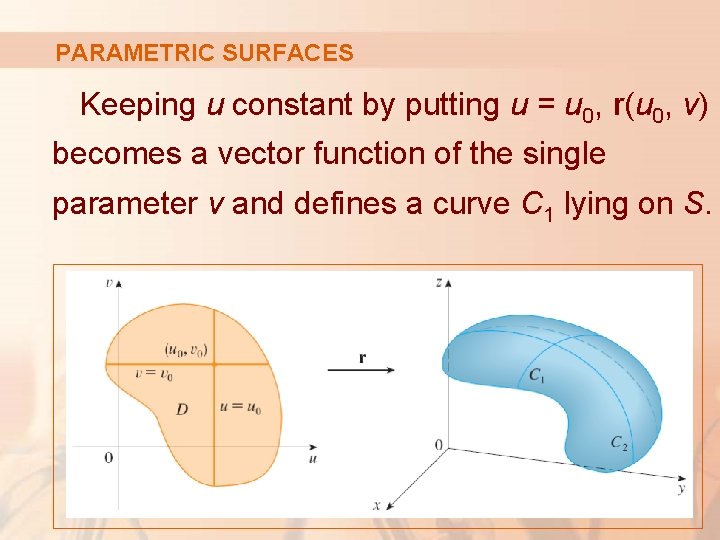
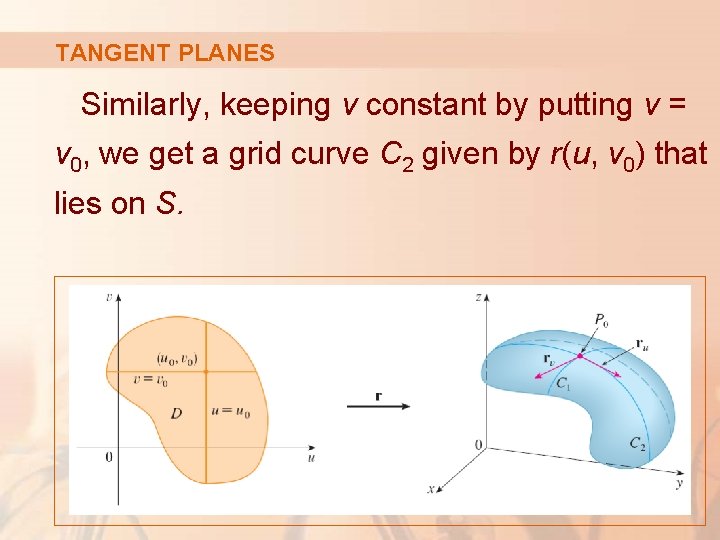
PARAMETRIC SURFACES If a parametric surface S is given by a vector function r(u, v), then there are two useful families of curves that lie on S—one with u constant and the other with v constant. § These correspond to vertical and horizontal lines in the uv-plane.

PARAMETRIC SURFACES Keeping u constant by putting u = u 0, r(u 0, v) becomes a vector function of the single parameter v and defines a curve C 1 lying on S.

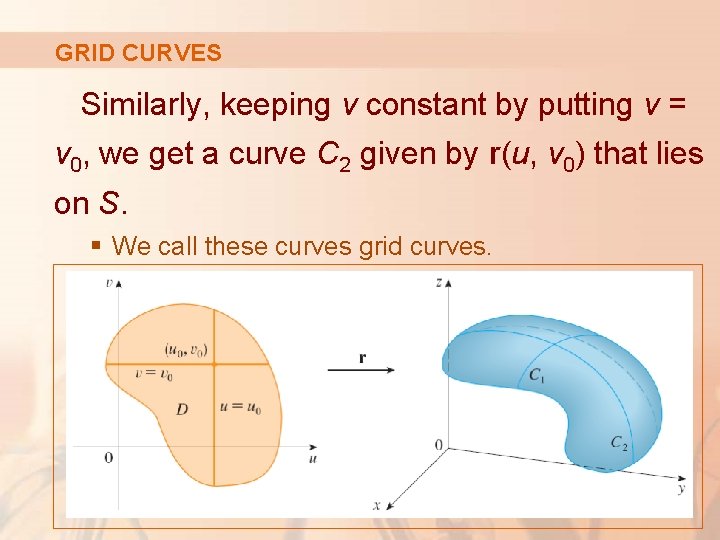
GRID CURVES Similarly, keeping v constant by putting v = v 0, we get a curve C 2 given by r(u, v 0) that lies on S. § We call these curves grid curves.

GRID CURVES In Example 1, for instance, the grid curves obtained by: § Letting u be constant are horizontal lines. § Letting v be constant are circles.

GRID CURVES In fact, when a computer graphs a parametric surface, it usually depicts the surface by plotting these grid curves—as we see in the following example.

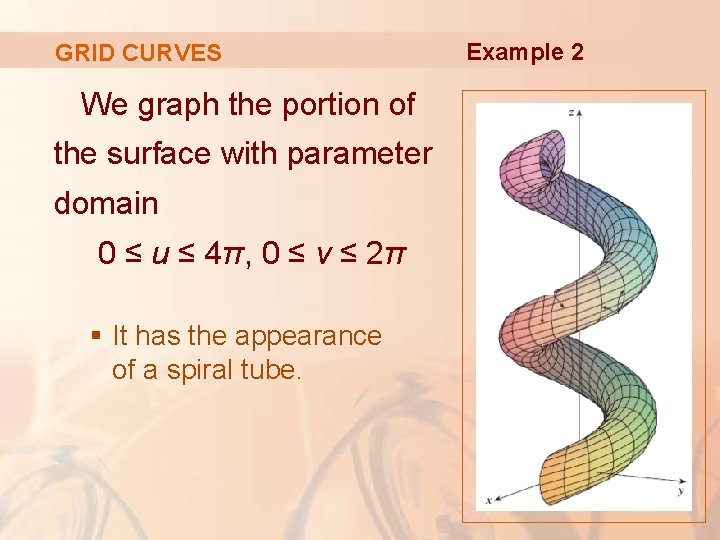
GRID CURVES Example 2 Use a computer algebra system to graph the surface r(u, v) = <(2 + sin v) cos u, (2 + sin v) sin u, u + cos v> § Which grid curves have u constant? § Which have v constant?

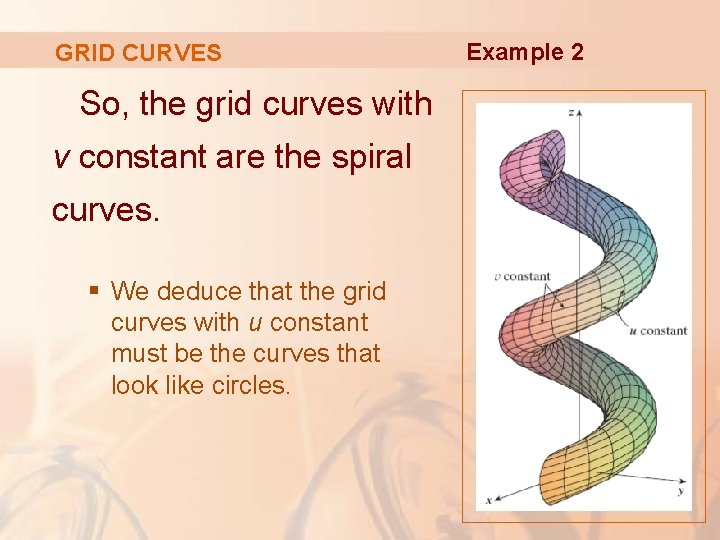
GRID CURVES We graph the portion of the surface with parameter domain 0 ≤ u ≤ 4π, 0 ≤ v ≤ 2π § It has the appearance of a spiral tube. Example 2

GRID CURVES Example 2 To identify the grid curves, we write the corresponding parametric equations: x = (2 + sin v) cos u y = (2 + sin v) sin u z = u + cos v

GRID CURVES Example 2 If v is constant, then sin v and cos v are constant. § So, the parametric equations resemble those of the helix in Example 4 in Section 13. 1

GRID CURVES So, the grid curves with v constant are the spiral curves. § We deduce that the grid curves with u constant must be the curves that look like circles. Example 2

Example 2 GRID CURVES Further evidence for this assertion is that, if u is kept constant, u = u 0, then the equation z = u 0 + cos v shows that the z-values vary from u 0 – 1 to u 0 + 1.

PARAMETRIC REPRESENTATION In Examples 1 and 2 we were given a vector equation and asked to graph the corresponding parametric surface. § In the following examples, however, we are given the more challenging problem of finding a vector function to represent a given surface. § In the rest of the chapter, we will often need to do exactly that.

PARAMETRIC REPRESENTATIONS Example 3 Find a vector function that represents the plane that: § Passes through the point P 0 with position vector r 0. § Contains two nonparallel vectors a and b.

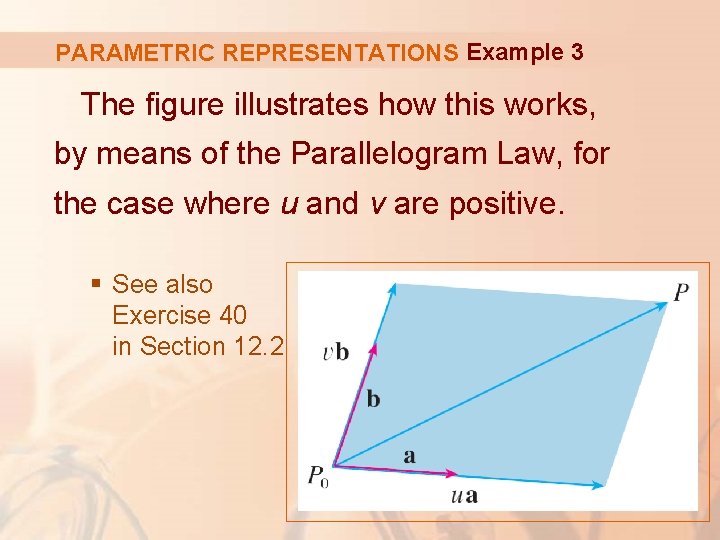
PARAMETRIC REPRESENTATIONS Example 3 If P is any point in the plane, we can get from P 0 to P by moving a certain distance in the direction of a and another distance in the direction of b. § So, there are scalars u and v such that: = ua + vb

PARAMETRIC REPRESENTATIONS Example 3 The figure illustrates how this works, by means of the Parallelogram Law, for the case where u and v are positive. § See also Exercise 40 in Section 12. 2

PARAMETRIC REPRESENTATIONS Example 3 If r is the position vector of P, then § So, the vector equation of the plane can be written as: r(u, v) = r 0 + ua + vb where u and v are real numbers.

PARAMETRIC REPRESENTATIONS Example 3 If we write r = <x, y, z> r 0 = <x 0, y 0, z 0> a = <a 1, a 2, a 3> b = <b 1, b 2, b 3> we can write the parametric equations of the plane through the point (x 0, y 0, z 0) as: x = x 0 + ua 1 + vb 1 y = y 0 + ua 2 + vb 2 z = z 0 + ua 3 + vb 3

PARAMETRIC REPRESENTATIONS Example 4 Find a parametric representation of the sphere x 2 + y 2 + z 2 = a 2 § The sphere has a simple representation ρ = a in spherical coordinates. § So, let’s choose the angles Φ and θ in spherical coordinates as the parameters (Section 15. 8).

PARAMETRIC REPRESENTATIONS Example 4 Then, putting ρ = a in the equations for conversion from spherical to rectangular coordinates (Equations 1 in Section 15. 8), we obtain: x = a sin Φ cos θ y = a sin Φ sin θ z = a cos Φ as the parametric equations of the sphere.

PARAMETRIC REPRESENTATIONS Example 4 The corresponding vector equation is: r(Φ, θ) = a sin Φ cos θ i + a sin Φ sin θ j + a cos Φ k § We have 0 ≤ Φ ≤ π and 0 ≤ θ ≤ 2π. § So, the parameter domain is the rectangle D = [0, π] x [0, 2π]

PARAMETRIC REPRESENTATIONS Example 4 The grid curves with: § Φ constant are the circles of constant latitude (including the equator). § θ constant are the meridians (semicircles), which connect the north and south poles.

APPLICATIONS—COMPUTER GRAPHICS One of the uses of parametric surfaces is in computer graphics.

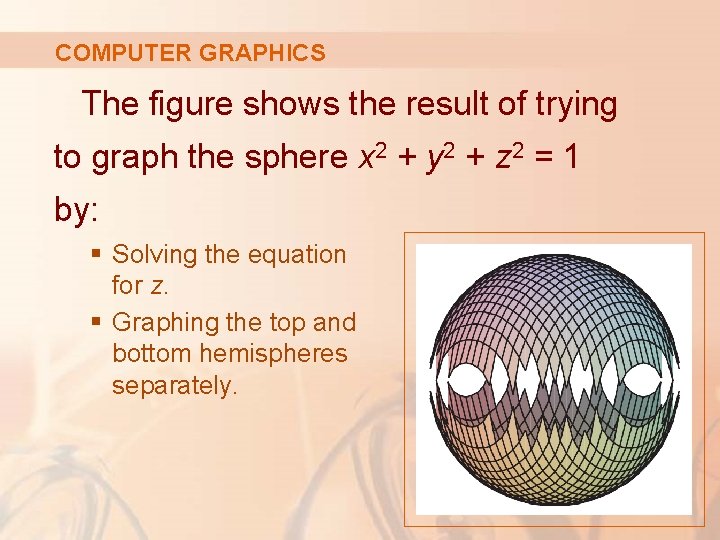
COMPUTER GRAPHICS The figure shows the result of trying to graph the sphere x 2 + y 2 + z 2 = 1 by: § Solving the equation for z. § Graphing the top and bottom hemispheres separately.

COMPUTER GRAPHICS Part of the sphere appears to be missing because of the rectangular grid system used by the computer.

COMPUTER GRAPHICS The much better picture here was produced by a computer using the parametric equations found in Example 4.

PARAMETRIC REPRESENTATIONS Example 5 Find a parametric representation for the cylinder x 2 + y 2 = 4 0≤z≤ 1 § The cylinder has a simple representation r = 2 in cylindrical coordinates. § So, we choose as parameters θ and z in cylindrical coordinates.

PARAMETRIC REPRESENTATIONS Example 5 Then the parametric equations of the cylinder are x = 2 cos θ where: § 0 ≤ θ ≤ 2π § 0≤z≤ 1 y = 2 sin θ z=z

PARAMETRIC REPRESENTATIONS Example 6 Find a vector function that represents the elliptic paraboloid z = x 2 + 2 y 2 § If we regard x and y as parameters, then the parametric equations are simply x=x y=y z = x 2 + 2 y 2 and the vector equation is r(x, y) = x i + y j + (x 2 + 2 y 2) k

PARAMETRIC REPRESENTATIONS In general, a surface given as the graph of a function of x and y—an equation of the form z = f(x, y)—can always be regarded as a parametric surface by: § Taking x and y as parameters. § Writing the parametric equations as x = x y = y z = f(x, y)

PARAMETRIZATIONS Parametric representations (also called parametrizations) of surfaces are not unique. § The next example shows two ways to parametrize a cone.

PARAMETRIZATIONS Example 7 Find a parametric representation for the surface that is, the top half of the cone z 2 = 4 x 2 + 4 y 2

PARAMETRIZATIONS E. g. 7—Solution 1 One possible representation is obtained by choosing x and y as parameters: x=x y=y § So, the vector equation is:

PARAMETRIZATIONS E. g. 7—Solution 2 Another representation results from choosing as parameters the polar coordinates r and θ. § A point (x, y, z) on the cone satisfies: x = r cos θ y = r sin θ

PARAMETRIZATIONS E. g. 7—Solution 2 So, a vector equation for the cone is r(r, θ) = r cos θ i + r sin θ j + 2 r k where: §r≥ 0 § 0 ≤ θ ≤ 2π

PARAMETRIZATIONS For some purposes, the parametric representations in Solutions 1 and 2 are equally good. In certain situations, though, Solution 2 might be preferable.

PARAMETRIZATIONS For instance, if we are interested only in the part of the cone that lies below the plane z = 1, all we have to do in Solution 2 is change the parameter domain to: 0≤r≤½ 0 ≤ θ ≤ 2π

SURFACES OF REVOLUTION Surfaces of revolution can be represented parametrically and thus graphed using a computer.
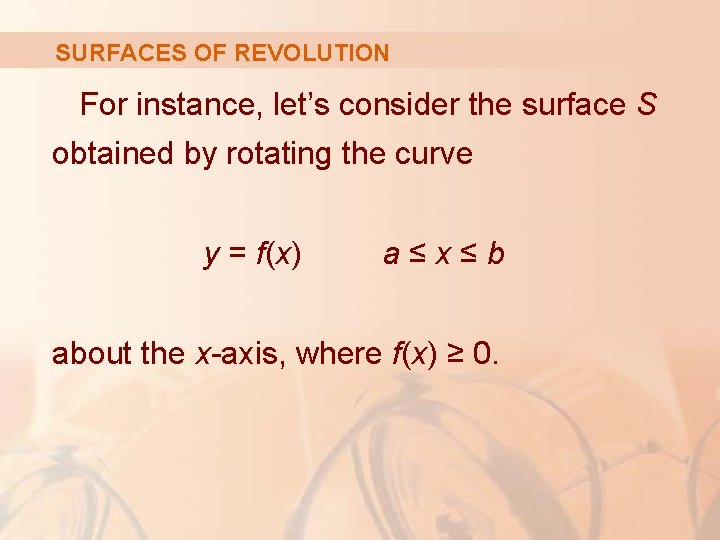
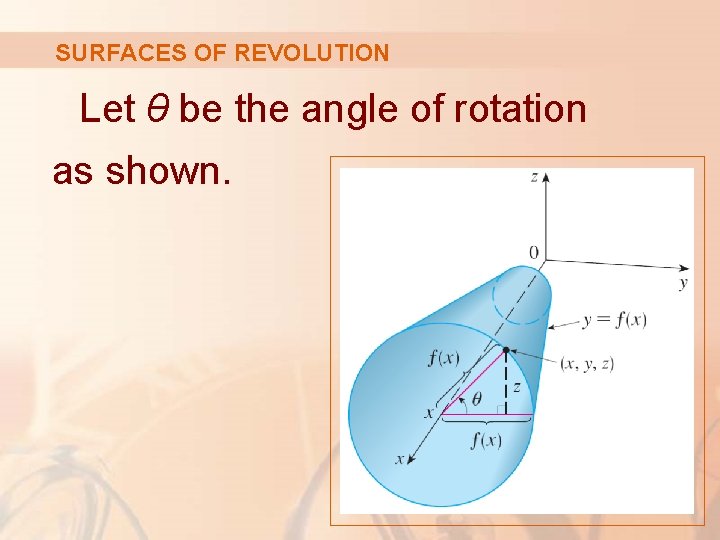
SURFACES OF REVOLUTION For instance, let’s consider the surface S obtained by rotating the curve y = f(x) a≤x≤b about the x-axis, where f(x) ≥ 0.

SURFACES OF REVOLUTION Let θ be the angle of rotation as shown.

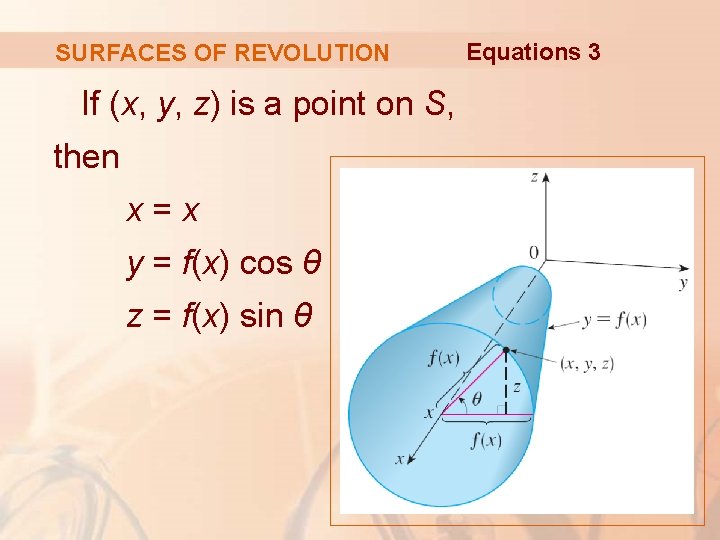
SURFACES OF REVOLUTION If (x, y, z) is a point on S, then x=x y = f(x) cos θ z = f(x) sin θ Equations 3

SURFACES OF REVOLUTION Thus, we take x and θ as parameters and regard Equations 3 as parametric equations of S. § The parameter domain is given by: a≤x≤b 0 ≤ θ ≤ 2π

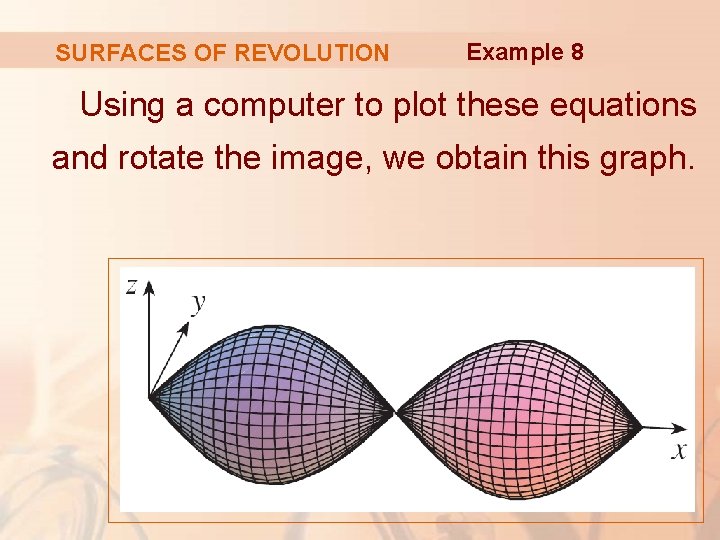
SURFACES OF REVOLUTION Example 8 Find parametric equations for the surface generated by rotating the curve y = sin x, 0 ≤ x ≤ 2π, about the x-axis. Use these equations to graph the surface of revolution.

Example 8 SURFACES OF REVOLUTION From Equations 3, § The parametric equations are: x=x y = sin x cos θ z = sin x sin θ § The parameter domain is: 0 ≤ x ≤ 2π 0 ≤ θ ≤ 2π

SURFACES OF REVOLUTION Example 8 Using a computer to plot these equations and rotate the image, we obtain this graph.

SURFACES OF REVOLUTION We can adapt Equations 3 to represent a surface obtained through revolution about the y- or z-axis. § See Exercise 30.

TANGENT PLANES We now find the tangent plane to a parametric surface S traced out by a vector function r(u, v) = x(u, v) i + y(u, v) j + z(u, v) k at a point P 0 with position vector r(u 0, v 0).

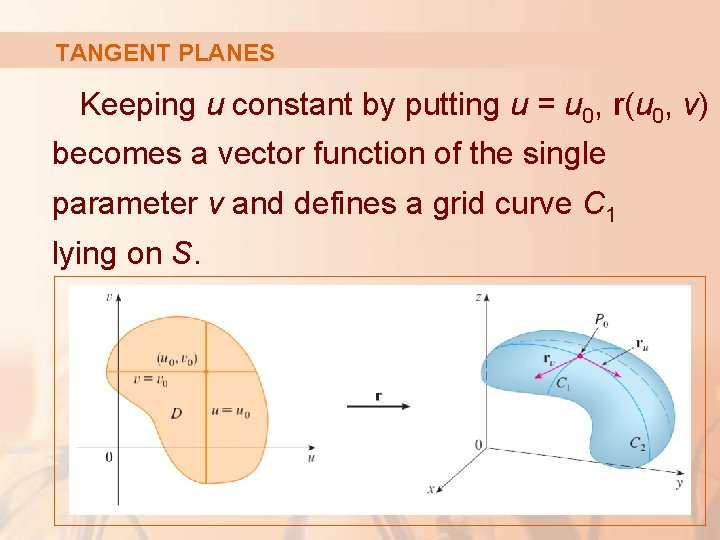
TANGENT PLANES Keeping u constant by putting u = u 0, r(u 0, v) becomes a vector function of the single parameter v and defines a grid curve C 1 lying on S.

TANGENT PLANES Equation 4 The tangent vector to C 1 at P 0 is obtained by taking the partial derivative of r with respect to v:

TANGENT PLANES Similarly, keeping v constant by putting v = v 0, we get a grid curve C 2 given by r(u, v 0) that lies on S.
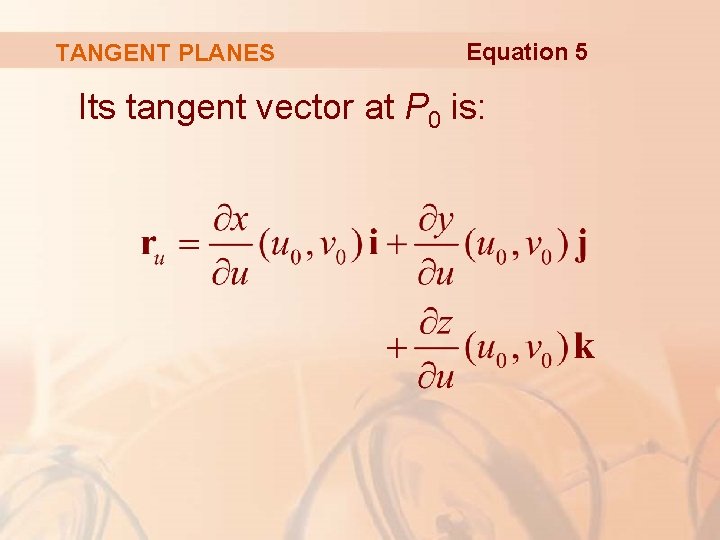
TANGENT PLANES Equation 5 Its tangent vector at P 0 is:

SMOOTH SURFACE If ru x rv is not 0, then the surface is called smooth (it has no “corners”). § For a smooth surface, the tangent plane is the plane that contains the tangent vectors ru and rv , and the vector ru x rv is a normal vector to the tangent plane.

Example 9 TANGENT PLANES Find the tangent plane to the surface with parametric equations x = u 2 y = v 2 at the point (1, 1, 3). z = u + 2 v

TANGENT PLANES Example 9 We first compute the tangent vectors:

TANGENT PLANES Example 9 Thus, a normal vector to the tangent plane is:

TANGENT PLANES Example 9 Notice that the point (1, 1, 3) corresponds to the parameter values u = 1 and v = 1. § So, the normal vector there is: – 2 i + 4 j + 4 k
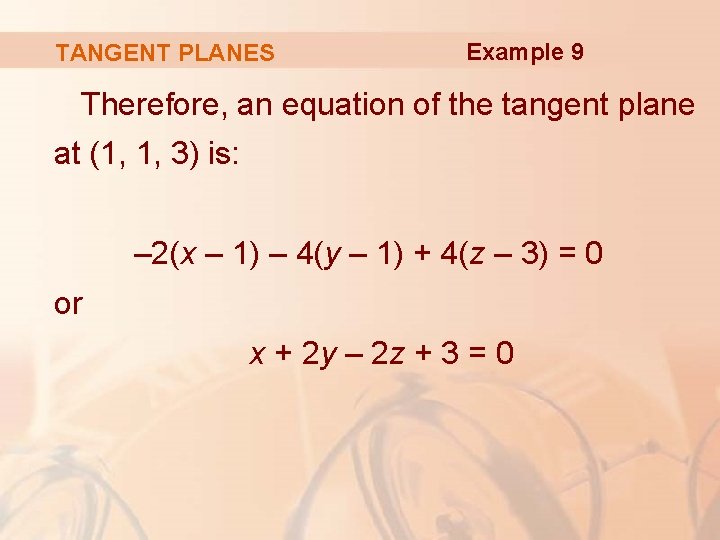
TANGENT PLANES Example 9 Therefore, an equation of the tangent plane at (1, 1, 3) is: – 2(x – 1) – 4(y – 1) + 4(z – 3) = 0 or x + 2 y – 2 z + 3 = 0

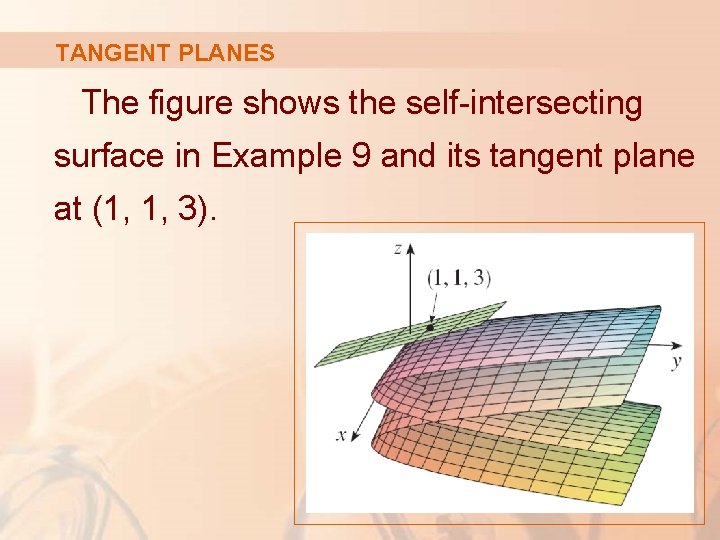
TANGENT PLANES The figure shows the self-intersecting surface in Example 9 and its tangent plane at (1, 1, 3).

SURFACE AREA Now, we define the surface area of a general parametric surface given by Equation 1.

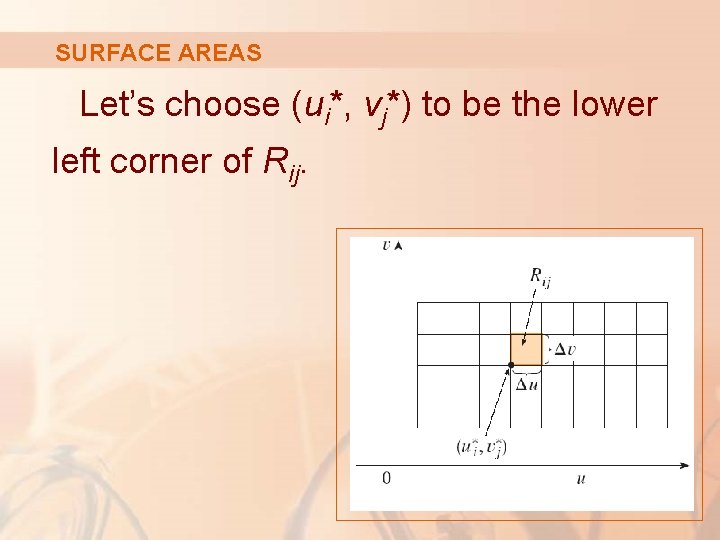
SURFACE AREAS For simplicity, we start by considering a surface whose parameter domain D is a rectangle, and we divide it into subrectangles Rij.

SURFACE AREAS Let’s choose (ui*, vj*) to be the lower left corner of Rij.

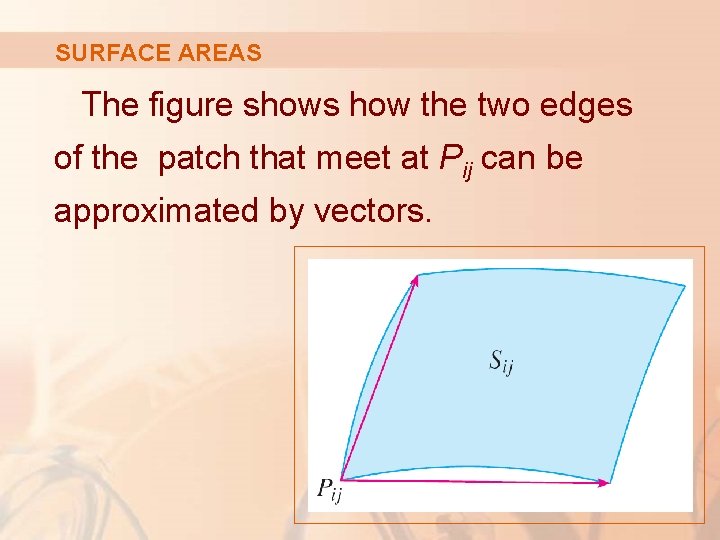
PATCH The part Sij of the surface S that corresponds to Rij is called a patch and has the point Pij with position vector r(ui*, vj*) as one of its corners.

SURFACE AREAS Let ru* = ru(ui*, vj*) and rv* = rv(ui*, vj*) be the tangent vectors at Pij as given by Equations 5 and 4.

SURFACE AREAS The figure shows how the two edges of the patch that meet at Pij can be approximated by vectors.

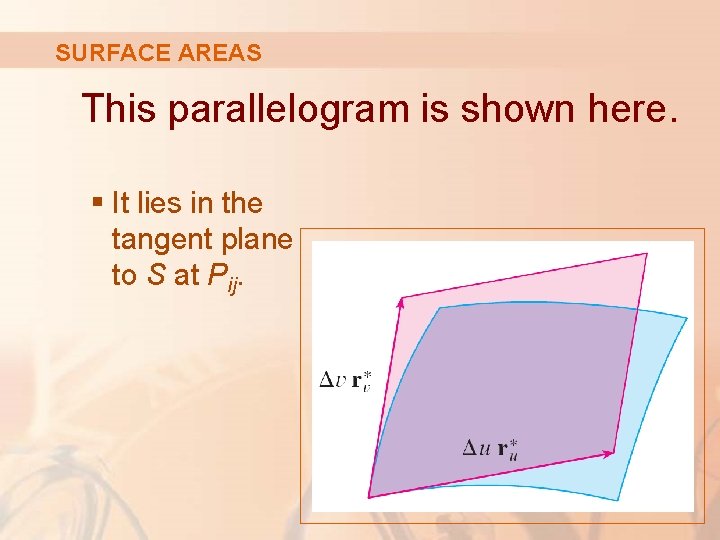
SURFACE AREAS These vectors, in turn, can be approximated by the vectors Δu ru* and Δv rv* because partial derivatives can be approximated by difference quotients. § So, we approximate Sij by the parallelogram determined by the vectors Δu ru* and Δv rv*.

SURFACE AREAS This parallelogram is shown here. § It lies in the tangent plane to S at Pij.

SURFACE AREAS The area of this parallelogram is: So, an approximation to the area of S is:

SURFACE AREAS Our intuition tells us that this approximation gets better as we increase the number of subrectangles. Also, we recognize the double sum as a Riemann sum for the double integral § This motivates the following definition.

SURFACE AREAS Definition 6 Suppose a smooth parametric surface S is: § Given by r(u, v) = x(u, v) i + y(u, v) j + z(u, v) k (u, v) D § Covered just once as (u, v) ranges throughout the parameter domain D.

SURFACE AREAS Definition 6 Then, the surface area of S is where:

SURFACE AREAS Example 10 Find the surface area of a sphere of radius a. § In Example 4, we found x = a sin Φ cos θ, y = a sin Φ sin θ, z = a cos Φ where the parameter domain is: D = {(Φ, θ) | 0 ≤ Φ ≤ π, 0 ≤ θ ≤ 2π)

SURFACE AREAS Example 10 We first compute the cross product of the tangent vectors:

SURFACE AREAS Example 10

SURFACE AREAS Example 10 Thus, since sin Φ ≥ 0 for 0 ≤ Φ ≤ π.

SURFACE AREAS Example 10 Hence, by Definition 6, the area of the sphere is:

SURFACE AREA OF THE GRAPH OF A FUNCTION Now, consider the special case of a surface S with equation z = f(x, y), where (x, y) lies in D and f has continuous partial derivatives. § Here, we take x and y as parameters. § The parametric equations are: x=x y=y z = f(x, y)

GRAPH OF A FUNCTION Thus, and Equation 7

GRAPH OF A FUNCTION Thus, we have: Equation 8

GRAPH OF A FUNCTION Formula 9 Then, the surface area formula in Definition 6 becomes:

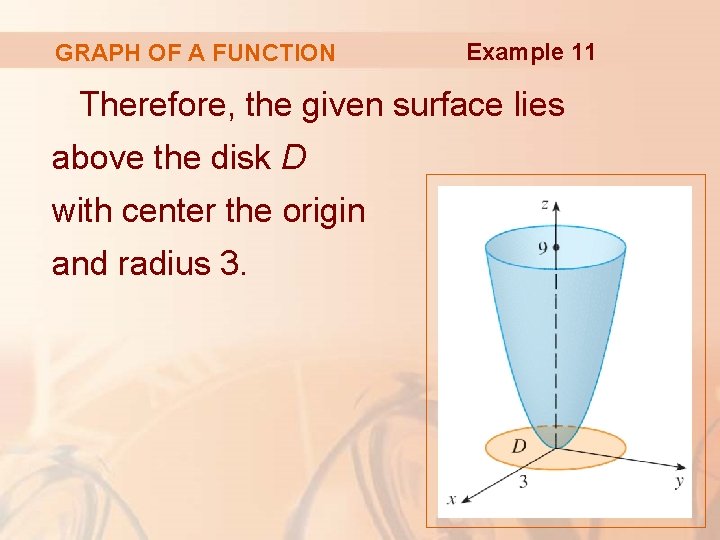
GRAPH OF A FUNCTION Example 11 Find the area of the part of the paraboloid z = x 2 + y 2 that lies under the plane z = 9. § The plane intersects the paraboloid in the circle x 2 + y 2 = 9, z = 9

GRAPH OF A FUNCTION Example 11 Therefore, the given surface lies above the disk D with center the origin and radius 3.

GRAPH OF A FUNCTION Using Formula 9, we have: Example 11

GRAPH OF A FUNCTION Example 11 Converting to polar coordinates, we obtain:

SURFACE AREA The question remains: § Is our definition of surface area (Definition 6) consistent with the surface area formula from single-variable calculus (Formula 4 in Section 8. 2)?

SURFACE AREA We consider the surface S obtained by rotating the curve y = f(x), a ≤ x ≤ b about the x-axis, where: § f(x) ≥ 0. § f’ is continuous.

SURFACE AREA From Equations 3, we know that parametric equations of S are: x=x y = f(x) cos θ a≤x≤b z = f(x) sin θ 0 ≤ θ ≤ 2π

SURFACE AREA To compute the surface area of S, we need the tangent vectors

SURFACE AREA Thus,

SURFACE AREA Hence, because f(x) ≥ 0.

SURFACE AREA Thus, the area of S is:

SURFACE AREA This is precisely the formula that was used to define the area of a surface of revolution in single-variable calculus (Formula 4 in Section 8. 2).
 This map becomes their window figure of speech
This map becomes their window figure of speech Sour cream walls is an example of pun
Sour cream walls is an example of pun In a kingdom far far away
In a kingdom far far away Far far away city
Far far away city Ixj
Ixj Vector identities
Vector identities Directional derivative in vector calculus
Directional derivative in vector calculus Fundamental theorem of vector calculus
Fundamental theorem of vector calculus A position vector is
A position vector is Partitioning a line segment formula
Partitioning a line segment formula Cosenos directores de un vector
Cosenos directores de un vector Resolution of vectors
Resolution of vectors Main proc far
Main proc far Imperative direct indirect
Imperative direct indirect Gone too far childnet
Gone too far childnet Football bell ringer
Football bell ringer Far side
Far side This is, by far, the most tedious way to create animations.
This is, by far, the most tedious way to create animations. Competition in contracting act
Competition in contracting act Nasa evm implementation handbook
Nasa evm implementation handbook Oracle flashback query how far back
Oracle flashback query how far back Ifr clearance template
Ifr clearance template Can far memory improve job throughput
Can far memory improve job throughput The far side comics
The far side comics So far away
So far away Grofar
Grofar Congratulations you made it this far
Congratulations you made it this far Wind ted hughes poem
Wind ted hughes poem När får man csn
När får man csn Chapter 16 the conquest of the far west
Chapter 16 the conquest of the far west As far as i m concerned
As far as i m concerned Far past participle
Far past participle Sos nba
Sos nba Comparison of adjectives generous
Comparison of adjectives generous Far 117 interpretations
Far 117 interpretations Far side rocket scientist
Far side rocket scientist Initation drama
Initation drama How far can we dig into the earth
How far can we dig into the earth Far point of emmetropic eye
Far point of emmetropic eye Summary of the void by muktibodh
Summary of the void by muktibodh Comic relief in macbeth act 2 scene 3
Comic relief in macbeth act 2 scene 3 Performance based payments
Performance based payments Får man skriva patientens namn i journalen
Får man skriva patientens namn i journalen Far-flung fossils activity answer key
Far-flung fossils activity answer key Gone too far childnet
Gone too far childnet Tale og skriftsprog
Tale og skriftsprog Mongols vs vikings
Mongols vs vikings John has hinted that he doesn't wish to remain in the group
John has hinted that he doesn't wish to remain in the group So far we have discussed
So far we have discussed Spider man far from home blockbuster
Spider man far from home blockbuster Huruf mad
Huruf mad Once upon a time long ago and far away
Once upon a time long ago and far away Far away
Far away The conquest of the far west
The conquest of the far west Superlative far
Superlative far The sun is the star at the center of the solar system
The sun is the star at the center of the solar system How far do you agree
How far do you agree Uniform contract format
Uniform contract format Plural of far
Plural of far Kaveh roshanbin far
Kaveh roshanbin far When nothing else could help love lifted me
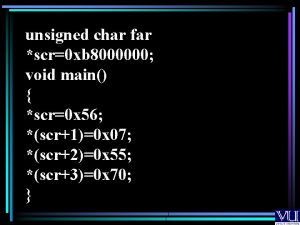
When nothing else could help love lifted me Char *scr
Char *scr Short adjectives
Short adjectives New words to learn
New words to learn 30 of the best far side cartoons of all time
30 of the best far side cartoons of all time How far is mercury from the sun
How far is mercury from the sun Vid körning i dagsljus på landsväg får du ett möte
Vid körning i dagsljus på landsväg får du ett möte Far contract closeout procedures
Far contract closeout procedures The great gatsby chapter 3 questions and answers
The great gatsby chapter 3 questions and answers Simon malynicz
Simon malynicz Per far felice una donna
Per far felice una donna Convert 68 f
Convert 68 f Far north is norway
Far north is norway Displacement
Displacement Hur många elektroner får plats i m skalet
Hur många elektroner får plats i m skalet Once apon a time in venice
Once apon a time in venice Lær excel 2007
Lær excel 2007 Far part 16 source selection
Far part 16 source selection Far eastern art
Far eastern art How far is a light year?
How far is a light year? Once in a faraway city
Once in a faraway city Let's discuss the story so far
Let's discuss the story so far How far is a high school free throw line
How far is a high school free throw line Milstrip
Milstrip Comparison of irregular adjectives
Comparison of irregular adjectives Trigonometry word problems
Trigonometry word problems Many comparative and superlative
Many comparative and superlative Far distances
Far distances Far method
Far method Comparative vs. superlative
Comparative vs. superlative Far point near point
Far point near point Agraph smells blood
Agraph smells blood Ciri-ciri mad asli
Ciri-ciri mad asli Hvordan får man en elefant ind i et køleskab
Hvordan får man en elefant ind i et køleskab Legekunstens far
Legekunstens far Qim far lab
Qim far lab Flumetrin
Flumetrin Flight duty period
Flight duty period The conquest of the far west
The conquest of the far west När får du köra vakt med flagga
När får du köra vakt med flagga Far 117 table b
Far 117 table b How far can you reach
How far can you reach Once a sinner far from jesus
Once a sinner far from jesus Far point
Far point Apa format header
Apa format header Perceptual defense in consumer behaviour
Perceptual defense in consumer behaviour How far did the inca empire stretch
How far did the inca empire stretch So far away
So far away