Jeopardy Review Game Volume Density and Surface Area

Jeopardy Review Game Volume, Density and Surface Area of a Sphere

Participation: Everyone should have their own piece of paper to write down each question. Show all work on your paper, they will be collected at the end of class and counted as a participation grade for today.

Note to Teacher: If at any time you need to return to the game board click the “I <3 Math” picture Pictures on the slides following the answers will also return you to the game board

Density Oh My! Grab Bag Volume Area 10 10 10 20 20 20 30 30 30 40 40 40 50 50 50

Back to the Game Board! Click here to return

Volume for 10 pts What are the volume formulas for prisms/cylinders and pyramids/cones?

Volume for 10 pts Answer Prisms/Cylinders: V=BH Pyramids/Cones: V= BH B=Area of Base H=Height of Solid

Back to the Game Board! Click here to return

Volume for 20 pts Find the volume 60 ft 20 ft 40 ft

Volume for 20 pts Answer V= (40)(20)(60) V= 48, 000 ft 3 60 ft 20 ft 40 ft

Back to the Game Board! Click here to return

Volume for 30 pts Find the volume (in terms of pi) 18 in 24 in

Volume for 30 pts Answer V=BH(1/2) r = 9 in V=(πr 2)(H)(1/2) V= (92π)24(1/2) V= (81π)12 V = 972 π in 3 18 in 24 in

Back to the Game Board! Click here to return

Volume for 40 pts Find the volume of the regular octagonal pyramid. a = 9 cm s = 15 cm 32 cm

Volume for 40 pts Answer V= BH V n = 8 a = 9 cm s = 15 cm 32 cm

Back to the Game Board! Click here to return

Volume for 50 pts Find the exact volume of the cone if the circumference of the base is 48πin 12 in

Volume for 50 pts Answer 12 in

Back to the Game Board! Click here to return

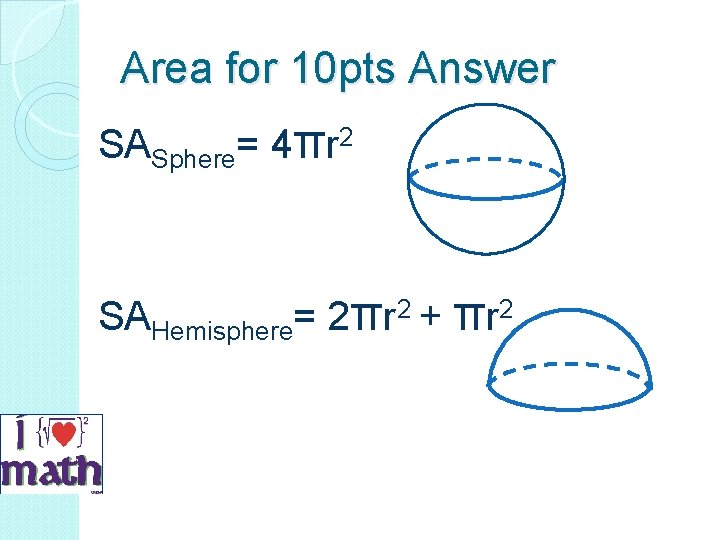
Area for 10 pts What are the Surface Area formulas for a Sphere and Hemisphere?

Area for 10 pts Answer SASphere= 4πr 2 SAHemisphere= 2πr 2 + πr 2

Back to the Game Board! Click here to return

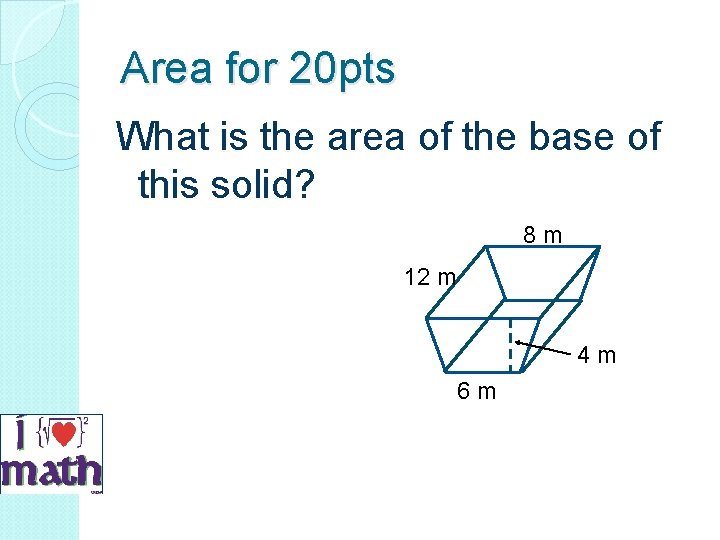
Area for 20 pts What is the area of the base of this solid? 8 m 12 m 4 m 6 m

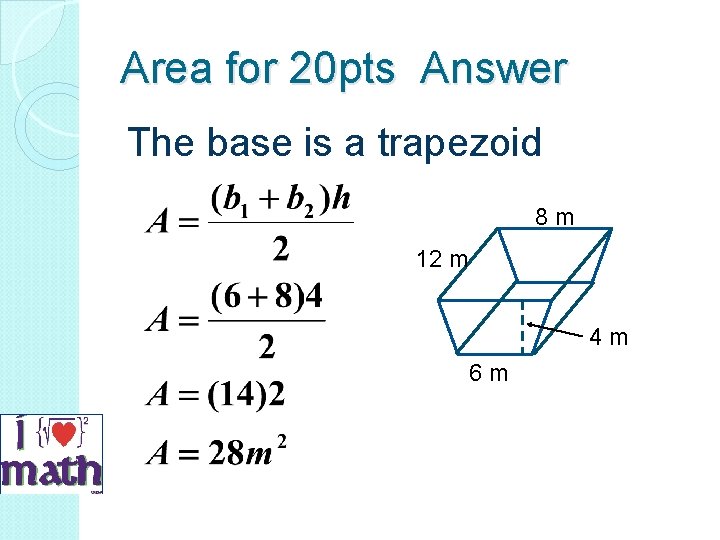
Area for 20 pts Answer The base is a trapezoid 8 m 12 m 4 m 6 m

Back to the Game Board! Click here to return

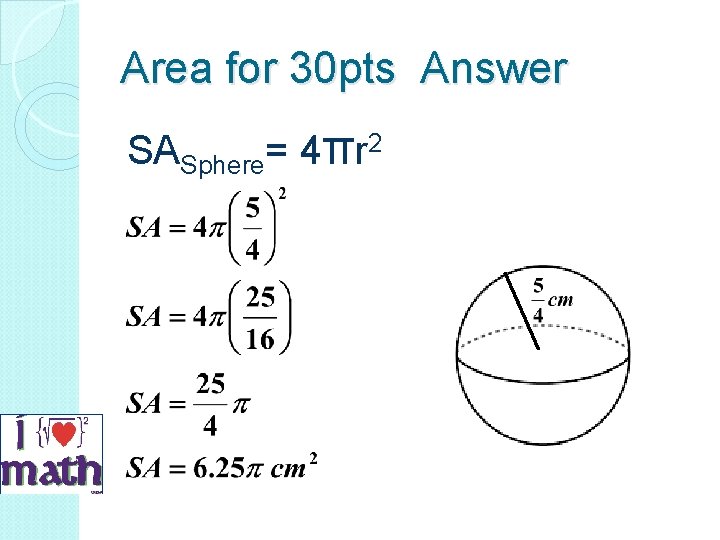
Area for 30 pts Find the exact surface area of this sphere

Area for 30 pts Answer SASphere= 4πr 2

Back to the Game Board! Click here to return

Area for 40 pts An igloo (hemisphere) has an outside circumference of 12πm. What is the exact surface area of the igloo’s outside?

Area for 40 pts Answer C=12πm r =6 m

Back to the Game Board! Click here to return

Area for 50 pts Find the exact surface area of the solid 3 in 5 in 7 in

Area for 50 pts Answer Outside Edge: r =5 2 Top/Bottom: A= πr Inside Edge: r =3 3 in 5 in Total: 7 in

Back to the Game Board! Click here to return

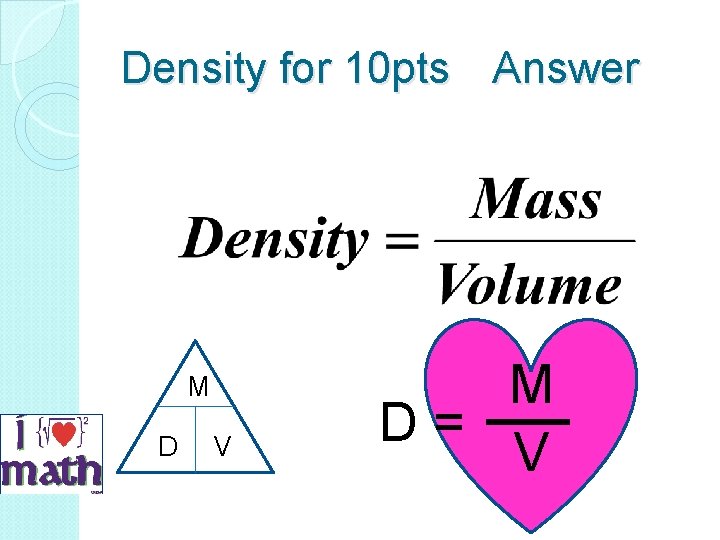
Density for 10 pts What is the formula for density?

Density for 10 pts Answer M D V M D = V

Back to the Game Board! Click here to return

Density for 20 pts If a rock has a mass of 18 grams and displaces 90 cm 3 of water. What is its density?

Density for 20 pts Answer M D = V

Back to the Game Board! Click here to return

Density for 30 pts A piece of metal weighs 351. 4 grams and causes the water level in a cylindrical container (r = 3 cm) to rise 1. 1 cm. What is the density of the piece of metal? (Round to the nearest tenth)

Density for 30 pts Answer

Back to the Game Board! Click here to return

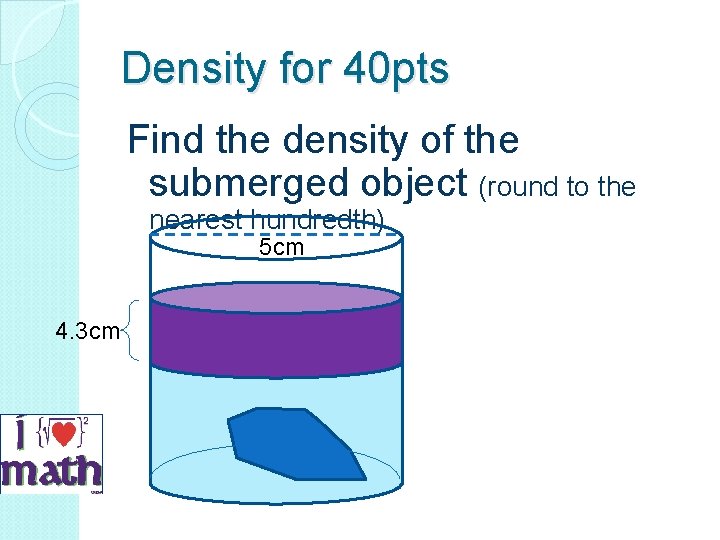
Density for 40 pts Find the density of the submerged object (round to the nearest hundredth) 5 cm 4. 3 cm

Density for 40 pts Answer 5 cm 4. 3 cm

Back to the Game Board! Click here to return

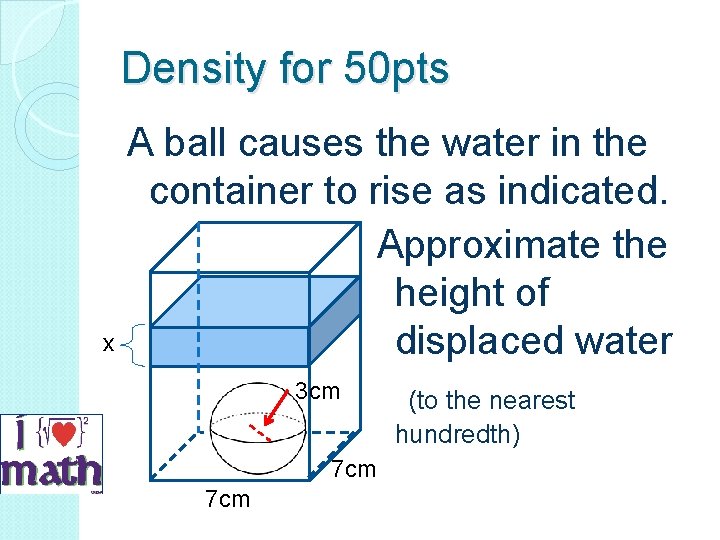
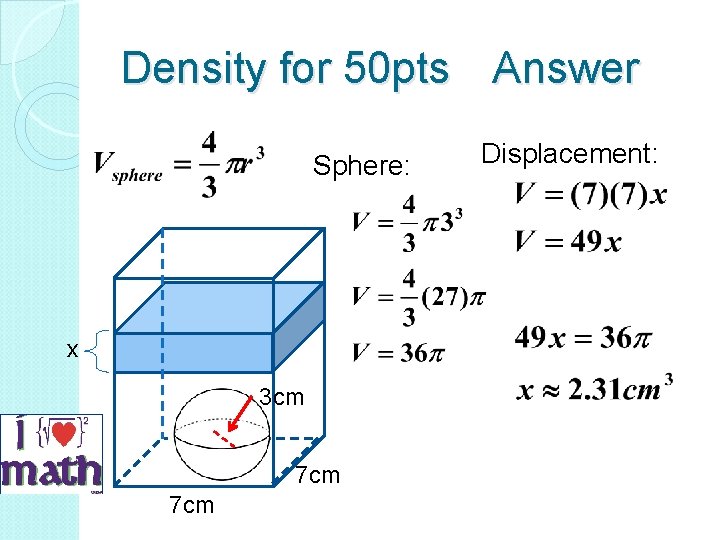
Density for 50 pts A ball causes the water in the container to rise as indicated. Approximate the height of x displaced water 3 cm 7 cm (to the nearest hundredth)

Density for 50 pts Answer Sphere: x 3 cm 7 cm Displacement:

Back to the Game Board! Click here to return

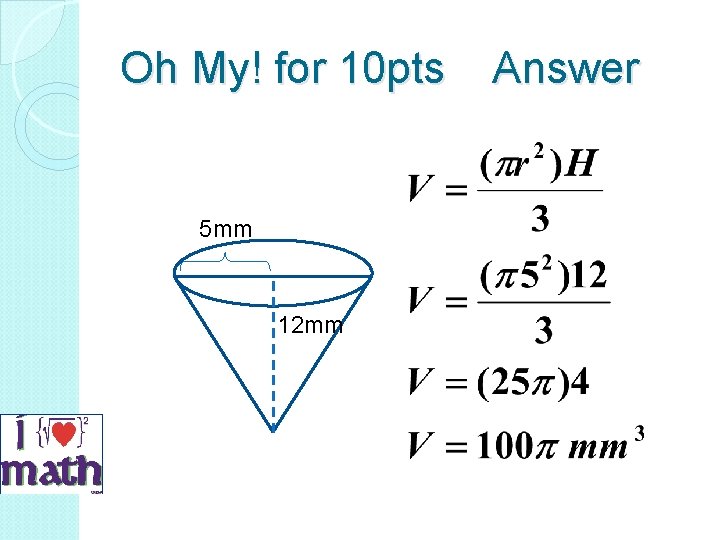
Oh My! for 10 pts Find the exact volume of the cone 5 mm 12 mm

Oh My! for 10 pts Answer 5 mm 12 mm

Back to the Game Board! Click here to return

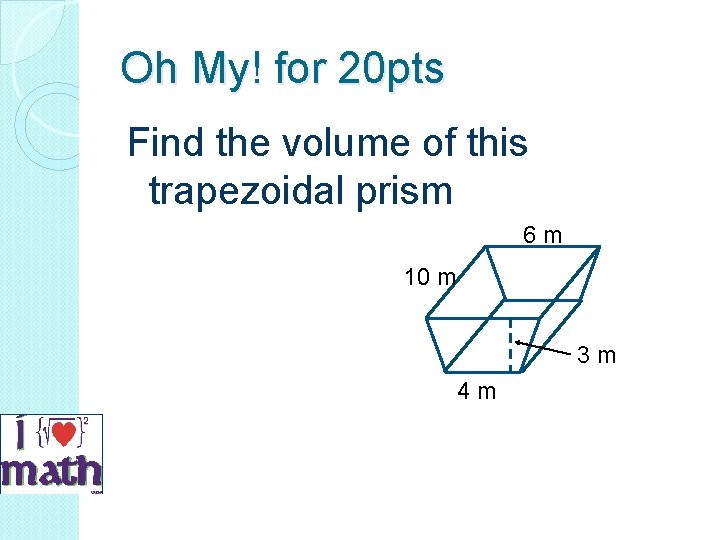
Oh My! for 20 pts Find the volume of this trapezoidal prism 6 m 10 m 3 m 4 m

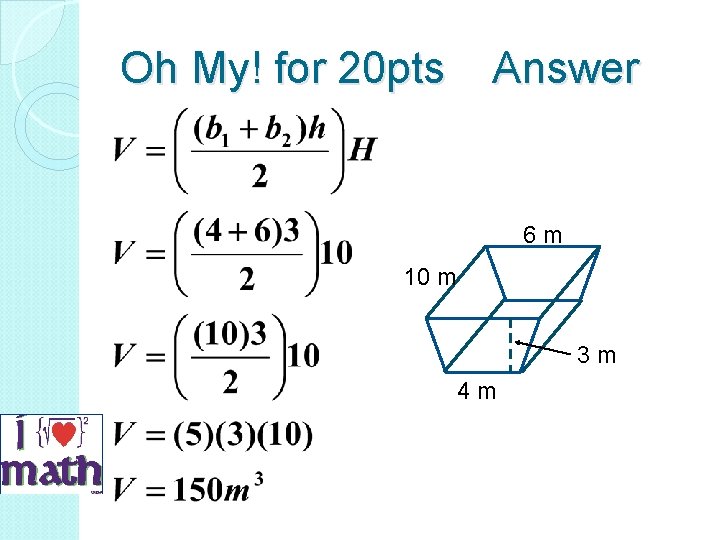
Oh My! for 20 pts Answer 6 m 10 m 3 m 4 m

Back to the Game Board! Click here to return

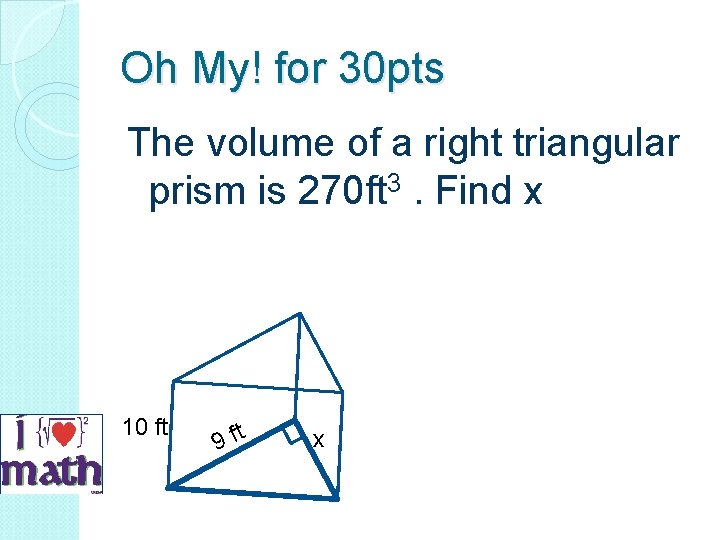
Oh My! for 30 pts The volume of a right triangular prism is 270 ft 3. Find x 10 ft 9 ft x

Oh My! for 30 pts Answer X = 6 ft 10 ft 9 ft x

Back to the Game Board! Click here to return

Oh My! for 40 pts The volume of a pyramid with an isosceles triangular base is 240 cm 3. The height of the triangle is cm and the base is 6 cm. What is the approximate height of the pyramid? (nearest hundredth)

Oh My! for 40 pts Answer H ≈ 46. 19 cm ? 3√ 3 6

Back to the Game Board! Click here to return

Oh My! for 50 pts Water world has a cylindrical water tower that is 150 ft tall and has a diameter of 80 ft. If they charge $0. 50 per gallon, how much money could they make from selling all the water in this tank? Round to the nearest whole dollar. (1 cubic foot = 7. 5 gallons)

Oh My! for 50 pts Answer 40 150

Back to the Game Board! Click here to return

Grab Bag for 10 pts Describe how we use displacement in math.

Grab Bag for 10 pts Answer It helps us find the volume of irregularly shaped objects. The volume of the displaced water is equal to the volume of the submerged object.

Back to the Game Board! Click here to return

Grab Bag for 20 pts If the foundation of a structure has a volume of 1350 ft 3 how many cubic yards of concrete did it take to make the foundation? (3 feet = 1 yard)

Grab Bag for 20 pts Answer 3 ft = 27 ft 3 3 ft 1 yd 3 1 yd 1 yd

Back to the Game Board! Click here to return

Grab Bag for 30 pts If the surface area of a sphere is 196 π cm 2, find its volume to the nearest hundredth.

Grab Bag for 30 pts Answer

Back to the Game Board! Click here to return

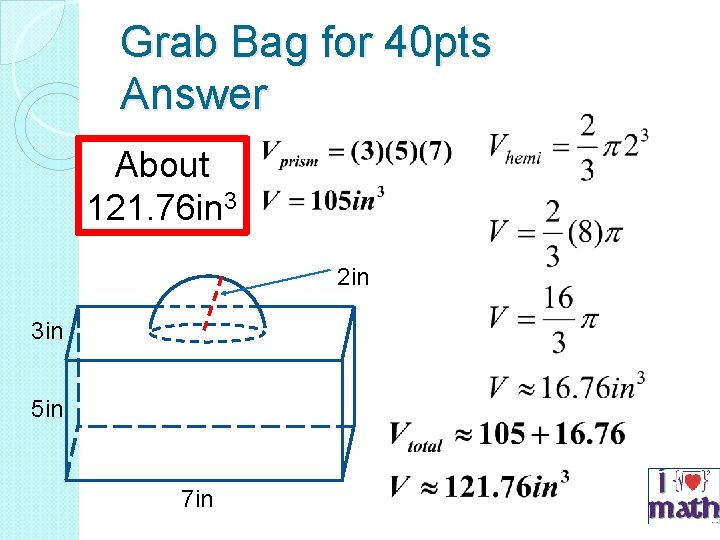
Grab Bag for 40 pts Find the approximate volume of the solid (nearest hundredth) 2 in 3 in 5 in 7 in

Grab Bag for 40 pts Answer About 121. 76 in 3 2 in 3 in 5 in 7 in

Back to the Game Board! Click here to return

Grab Bag for 50 pts This toy part is made of plastic. The outer-hemisphere diameter is 5 in and the inner-hemisphere diameter is 4 in. Find the volume of the plastic. 5 in 4 in (Round to the nearest thousandth)

Grab Bag for 50 pts Answer Outer: Inner: 15. 97 in 3 5 in 4 in Total:

Back to the Game Board! Click here to return