Hypothesis Testing with Two Samples Section 3 Testing






































- Slides: 42

Hypothesis Testing with Two Samples

Section 3 Testing the Difference Between Means (Dependent Samples) .

• How to perform a t-test to test the mean of the difference for a population of paired data .

t-Test for the Difference Between Means • To perform a two-sample hypothesis test with dependent samples, the difference between each data pair is first found: • d = x 1 – x 2 Difference between entries for a data pair • The test statistic is the mean of these differences. Mean of the differences between paired § data entries in the dependent samples .

t-Test for the Difference Between Means • .

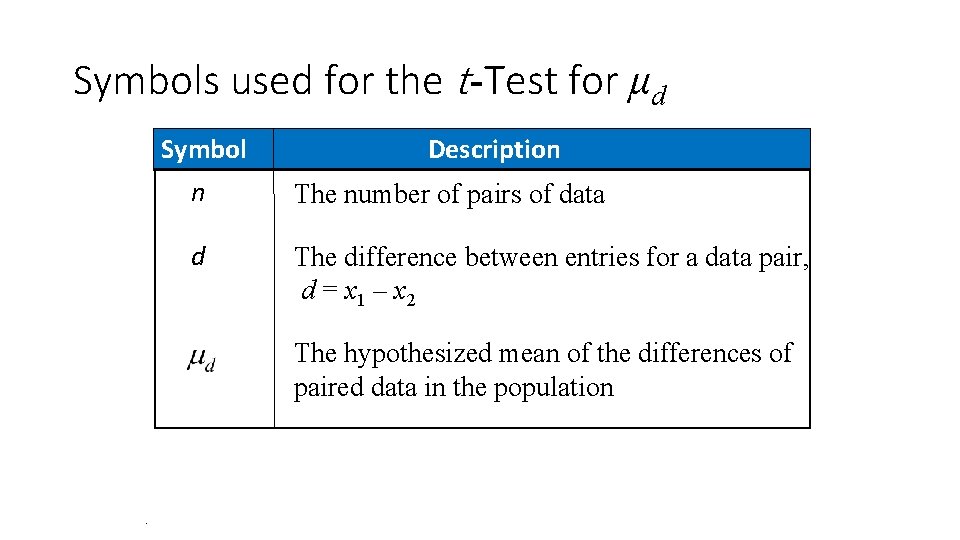
Symbols used for the t-Test for μd Symbol Description n The number of pairs of data d The difference between entries for a data pair, d = x 1 – x 2 The hypothesized mean of the differences of paired data in the population .

Symbols used for the t-Test for μd Symbol Description The mean of the differences between the paired data entries in the dependent samples sd . The standard deviation of the differences between the paired data entries in the dependent samples

t-Test for the Difference Between Means A t-test can be used to test the difference of two population means when these conditions are met. 1. The samples are random. 2. The samples are dependent (paired). 3. The populations are normally distributed or the number n ≥ 30. .

t-Test for the Difference Between Means • The test statistic is • The standardized test statistic is • The degrees of freedom are d. f. = n – 1 .

t-Test for the Difference Between Means (Dependent Samples) In Words In Symbols 1. Verify that the samples are random and dependent, and either the populations are normally distributed or n 30. 2. State the claim mathematically and verbally. Identify the null and alternative hypotheses. 3. Specify the level of significance. . State H 0 and Ha. Identify .

t-Test for the Difference Between Means (Dependent Samples) In Words 4. Identify the degrees of freedom. 5. Determine the critical value(s). 6. Determine the rejection region(s). 7. Calculate and . In Symbols d. f. = n – 1 Use Table 5 in Appendix B.

t-Test for the Difference Between Means (Dependent Samples) In Words In Symbols 8. Find the standardized test statistic and sketch the sampling distribution. 9. Make a decision to reject or fail to reject the null hypothesis. 10. Interpret the decision in the context of the original claim. . If t is in the rejection region, then reject H 0. Otherwise, fail to reject H 0.

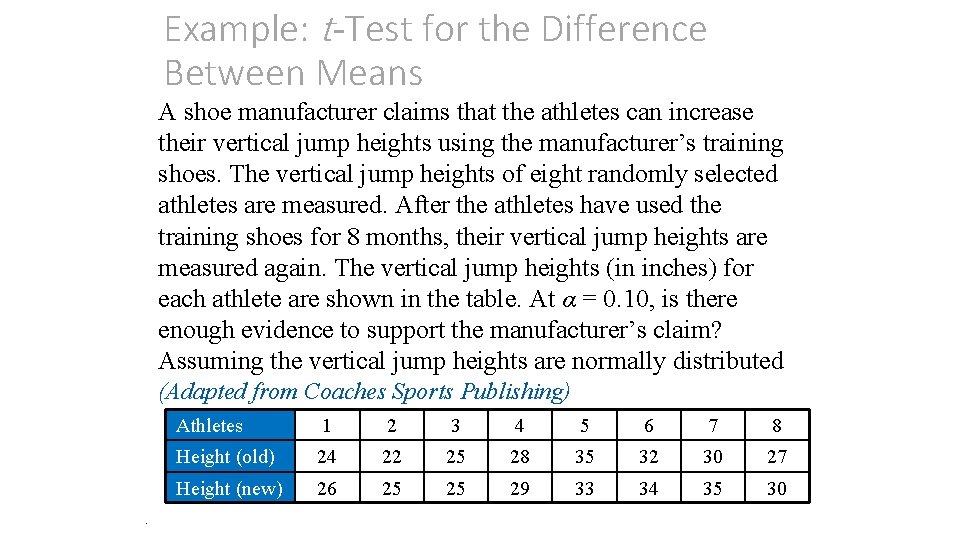
Example: t-Test for the Difference Between Means A shoe manufacturer claims that the athletes can increase their vertical jump heights using the manufacturer’s training shoes. The vertical jump heights of eight randomly selected athletes are measured. After the athletes have used the training shoes for 8 months, their vertical jump heights are measured again. The vertical jump heights (in inches) for each athlete are shown in the table. At α = 0. 10, is there enough evidence to support the manufacturer’s claim? Assuming the vertical jump heights are normally distributed (Adapted from Coaches Sports Publishing) . Athletes 1 2 3 4 5 6 7 8 Height (old) 24 22 25 28 35 32 30 27 Height (new) 26 25 25 29 33 34 35 30

Solution: Two-Sample t-Test for the Difference Between Means Solution: Because the samples are random and dependent, and the populations are normally distributed, you can use the t-test. The claim is that “athletes can increase their vertical jump heights. ” In other words, the manufacturer claims that an athlete’s vertical jump height before using the shoes will be less than the athlete’s vertical jump height after using the shoes. Each difference is given by d = (jump height before shoes) – (jump height after shoes). The null and alternative hypotheses are H 0: md 0 and Ha: md < 0. (Claim) .

Solution: Two-Sample t-Test for the Difference Between Means • .

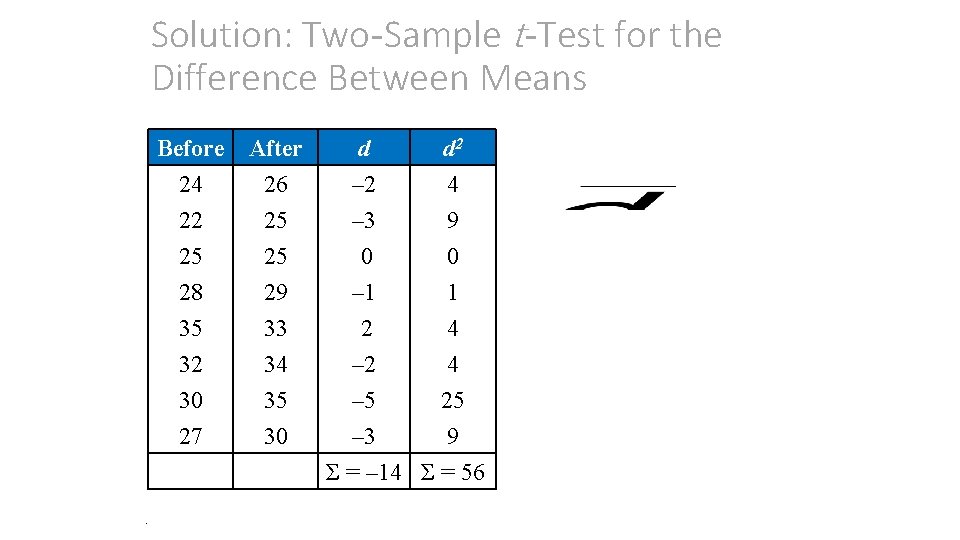
Solution: Two-Sample t-Test for the Difference Between Means Before After 24 26 22 25 25 25 28 35 32 30 27 . 29 33 34 35 30 d – 2 – 3 0 d 2 4 9 0 – 1 1 2 4 – 5 25 – 3 9 Σ = – 14 Σ = 56

Solution: Two-Sample t-Test for the Difference Between Means The standardized test statistic is The figure shows the location of the rejection region and the standardized test statistic t. Because t is in the rejection region, you reject the null hypothesis. .

Solution: Two-Sample t-Test for the Difference Between Means There is enough evidence at the 10% level of significance to support the shoe manufacturer’s claim that athletes can increase their vertical jump heights using the manufacturer’s training shoes. .

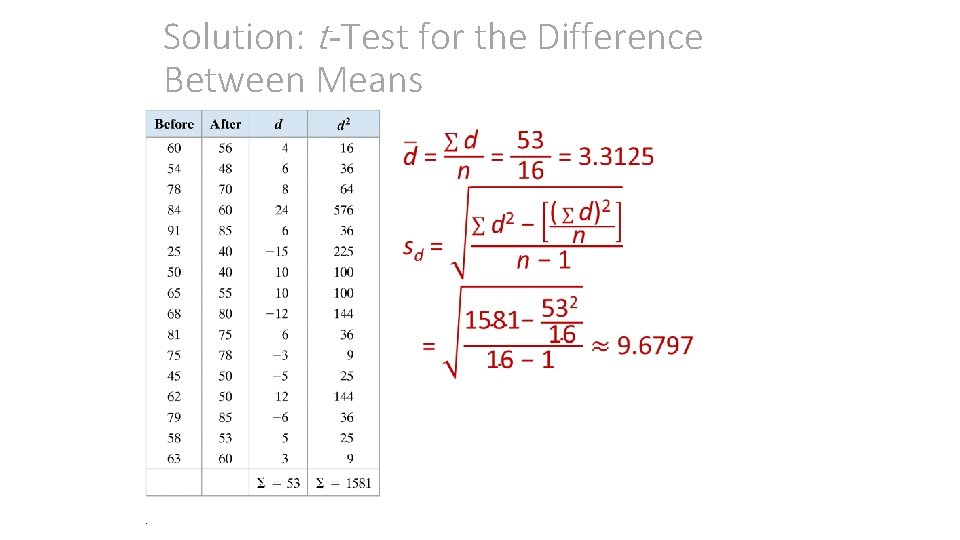
Example: t-Test for the Difference Between Means The campaign staff for a state legislator wants to determine whether the legislator’s performance rating (0 – 100) has changed from last year to this year. The table below shows the legislator’s performance ratings from the same 16 randomly selected voters for last year and this year. At = 0. 01, is there enough evidence to conclude that the legislator’s performance rating has changed? Assume the performance ratings are normally distributed. .

Solution: t-Test for the Difference Between Means Solution: Because the samples are random and dependent, and the populations are normally distributed, you can use the t-test. If there is a change in the legislator’s rating, then there will be a difference between last year’s ratings and this year’s ratings. Because the legislator wants to determine whethere is a difference, the null and alternative hypotheses are H 0: md = 0 and Ha: md 0. (Claim) .

Solution: t-Test for the Difference Between Means • .

Solution: t-Test for the Difference Between Means • .

Solution: t-Test for the Difference Between Means • You can check this result using technology.

Solution: t-Test for the Difference Between Means The figure shows the location of the rejection region and the standardized test statistic t. Because t is not in the rejection region, you fail to reject the null hypothesis. There is not enough evidence at the 1% level of significance to conclude that the legislator’s performance rating has changed. .

Section 4 Testing the Difference Between Proportions .

• How to perform a two-sample z-test for the difference between two population proportions p 1 and p 2 .

Two-Sample z-Test for Proportions • Used to test the difference between two population proportions, p 1 and p 2. • Three conditions are required to conduct the test. 1. The samples must be randomly selected. 2. The samples must be independent. 3. The samples must be large enough to use a normal sampling distribution. That is, n 1 p 1 5, n 1 q 1 5, n 2 p 2 5, and n 2 q 2 5. .

Two-Sample z-Test for the Difference Between Proportions • If these conditions are met, then the sampling distribution for is a normal distribution • Mean: • A weighted estimate of p 1 and p 2 can be found by using • Standard error: . ,

Two-Sample z-Test for the Difference Between Proportions where.

Two-Sample z-Test for the Difference Between Proportions In Words In Symbols 1. Verify that the samples are random and independent. . 2. Find the weighted estimate of p 1 and p 2. Verify that are at least 5. . 3. State the claim mathematically and verbally. Identify the null and alternative hypotheses. State H 0 and Ha. 4. Specify the level of significance. Identify .

Two-Sample z-Test for the Difference Between Proportions In Words 5. Determine the critical value(s). 6. Determine the rejection region(s). 7. Find the standardized test statistic and sketch the sampling distribution. . In Symbols Use Table 4 in Appendix B.

Two-Sample z-Test for the Difference Between Proportions In Words 8. Make a decision to reject or fail to reject the null hypothesis. 9. Interpret the decision in the context of the original claim. . In Symbols If z is in the rejection region, reject H 0. Otherwise, fail to reject H 0.

Example: Two-Sample z-Test for the Difference Between Proportions • .

Solution: Two-Sample z-Test for the Difference Between Proportions • .

Solution: Two-Sample z-Test for the Difference Between Proportions •

Solution: Two-Sample z-Test for the Difference Between Proportions • .

Solution: Two-Sample z-Test for the Difference Between Proportions The figure below shows the location of the rejection regions and the standardized test statistic z. Because z is in the rejection region, you reject the null hypothesis. There is enough evidence at the 10% level of significance to reject the claim that the proportion of occupants who wear seat belts is the same for passenger cars and pickup trucks. .

Example: Two-Sample z-Test for the Difference Between Proportions A medical research team conducted a study to test the effect of a cholesterol reducing medication. At the end of the study, the researchers found that of the 4700 randomly selected subjects who took the medication, 301 died of heart disease. Of the 4300 randomly selected subjects who took a placebo, 357 died of heart disease. At α = 0. 01 can you conclude that the death rate due to heart disease is lower for those who took the medication than for those who took the placebo? (Adapted from New England Journal of Medicine) .

Solution: Two-Sample z-Test for the Difference Between Proportions • .

Solution: Two-Sample z-Test for the Difference Between Proportions •

Solution: Two-Sample z-Test for the Difference Between Proportions The standardized test statistic is .

Solution: Two-Sample z-Test for the Difference Between Proportions The figure below shows the location of the rejection region and the standardized test statistic z. Because z is in the rejection region, you reject the null hypothesis. There is enough evidence at the 1% level of significance to support the claim that the death rate due to heart disease is lower for those who took the medication than for those who took the placebo. .
 A dietitian wishes to see if a person's cholesterol
A dietitian wishes to see if a person's cholesterol Inferences based on two samples
Inferences based on two samples Syarat uji median
Syarat uji median What is the null hypothesis
What is the null hypothesis Developing null and alternative hypothesis
Developing null and alternative hypothesis Site:slidetodoc.com
Site:slidetodoc.com Protoplanet hypothesis weakness
Protoplanet hypothesis weakness The language of hypothesis testing
The language of hypothesis testing Inference hypothesis testing
Inference hypothesis testing Anova
Anova Hypothesis testing assignment
Hypothesis testing assignment Hypothesis testing
Hypothesis testing Critical value hypothesis testing
Critical value hypothesis testing Hypothesis testing assumptions
Hypothesis testing assumptions Hypothesis testing formula
Hypothesis testing formula Goal of hypothesis testing
Goal of hypothesis testing Hypothesis type 1 error
Hypothesis type 1 error Formula for hypothesis testing
Formula for hypothesis testing Six steps of hypothesis testing
Six steps of hypothesis testing What is the claim in hypothesis testing
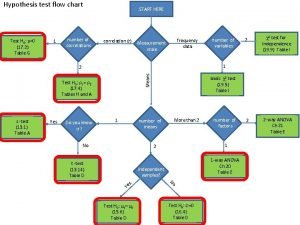
What is the claim in hypothesis testing Hypothesis testing flowchart
Hypothesis testing flowchart Chapter 8 hypothesis testing
Chapter 8 hypothesis testing Chapter 7 hypothesis testing with one sample answers
Chapter 7 hypothesis testing with one sample answers Hypothesis testing for population proportion
Hypothesis testing for population proportion Slope hypothesis testing
Slope hypothesis testing Hypothesis testing business statistics
Hypothesis testing business statistics Hypothesis testing a level maths
Hypothesis testing a level maths Manifold hypothesis
Manifold hypothesis Hypothesis testing in r
Hypothesis testing in r Phantoms in statistics
Phantoms in statistics Hypothesis testing in r
Hypothesis testing in r Anova test
Anova test Hypothesis testing excel
Hypothesis testing excel Create a meme about concepts in hypothesis testing
Create a meme about concepts in hypothesis testing Hypothesis testing for variance
Hypothesis testing for variance Testing of hypothesis
Testing of hypothesis Categorical hypothesis testing
Categorical hypothesis testing Statistical test meaning
Statistical test meaning Causal hypothesis testing
Causal hypothesis testing Kari is testing the hypothesis
Kari is testing the hypothesis Hypothesis examples
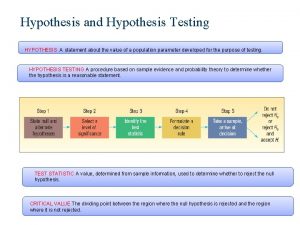
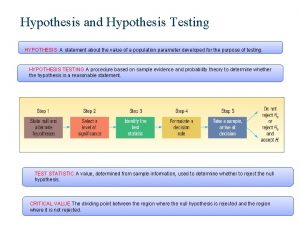
Hypothesis examples Logic of hypothesis testing
Logic of hypothesis testing Hypothesis testing notation
Hypothesis testing notation