Statistics Hypothesis Test PHANTOMS P Parameter H Hypotheses

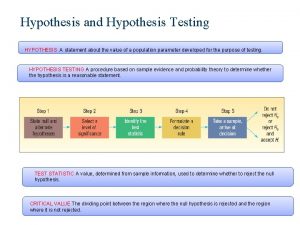
Statistics Hypothesis Test PHANTOMS P Parameter H Hypotheses A Assumptions N Name the test T Test statistic O Obtain p-value M Make decision S State conclusion in context

Is the coin Fair? You suspect that you have a weighted coin. You flip the coin 220 times and find 124 heads. Is there enough statistical evidence to declare the coin unfair? Let p = the true proportion of coin tosses landing on heads. One Proportion z – Test Ho: p = 0. 5 Ha: p ≠ 0. 5 1. SRS – The data was collected randomly by a chance event 2. Appr. Normal: 220 (0. 5)=110 ≥ 10 AND 220 (1 – (0. 5))=110 ≥ 10 Since our p-value is greater than 0. 05 we “FAIL to REJECT H 0“. There is not sufficient evidence to conclude the coin is unfair.

p = The true proportion of Hispanics called for jury duty in the county. H 0 : p = 0. 19 HA : p < 0. 19

One Proportion z – Test p = The true proportion of Hispanics called for jury duty in the county. H 0 : p = 0. 19 HA : p < 0. 19 Since the P-value = 0. 0793 is high p>0. 05, we fail to reject the null hypothesis. There is NO convincing evidence that Hispanics are underrepresented in the jury selection system. SRS: potential jurors are called randomly from all of the residents. Success/Failure condition: np= (72)(0. 19) = 13. 68 and n(1 – p) = (72)(0. 81) = 58. 32 are both > 10, so the sample is large enough.

WHAT PERCENT OF THE EARTH IS COVERED WITH WATER?

One Proportion Significance Test Is there evidence that the proportion of the earth that is covered with water is different than 0. 78 p = The true proportion of earth’s surface that is covered with water. One H 0: p = 0. 78 Proportion Ha: p ≠ 0. 78 z – Test 1. 2. 3. SRS – The data was collected randomly Population of potential volleys is ≥ 10 · n n · (0. 78) ≥ 10 AND n · (1 – (0. 78)) ≥ 10 Since the P-Value is NOT less than 0. 05 , we fail to REJECT H 0 There is Since no evidence to support the prop. of Earth’s water is NOTto 78% the P-Value is lessthat than 0. 05 There is strong evidence REJECT H 0. The claim that exactly 0. 78 of the Earth is covered by water is not supported.

H 0 : p = 0. 40 (p=The proportion of female executives. ) HA : p < 0. 40

H 0 : p = 0. 40 (The proportion of female executives. ) HA : p < 0. 40 One Proportion z – Test Randomization condition: Executives were not chosen randomly, 10% condition: Population of employees at the company > 10(43) Success/Failure condition: np= (43)(0. 40) = 17. 2 and n(1 – p) = (43)(0. 60) = 25. 8 are both >10, so the sample is large enough. The conditions have not all been satisfied, so a Normal model may or may not be valid, so we continue with Caution

Since the P-value = 0. 0955 is high (p>0. 05), we fail to reject the H 0. There is little evidence to suggest proportion of female executives is any different from the overall proportion of 40% female employees at the company.

HW: Page 472: 25 -28

HW: Page 472: 25 -28

WARM – UP An insurance company checks police records on 582 accidents selected at random. Teenagers were involved in 91 of them. a. ) Find the 95% Confidence Interval for the true % of accidents that involve teens. (Follow all steps) b. )A Politician interested in raising the drivers licenses age claims that one out of every five (p =. 20) auto accidents is due to teenagers. Is there supporting evidence that the proportion is different than this?

a. )An insurance company checks police records on 582 accidents selected at random. Teenagers were involved in 91 of them. Find the 95% Confidence Interval for the % of accidents that involved teens. (Follow all steps) p = The true proportion of auto accidents involving teenagers. 1. SRS – Stated 2. Population of National Auto Accidents ≥ 10(582) 3. 582(. 1564) ≥ 10 582(1 -. 1564) ≥ 10 One Proportion Z– Conf. Int. We can be 95% confident that the true proportion of accidents involving teenage drivers is between 12. 7% and 18. 6%

b. ) An insurance company checks police records on 582 accidents selected at random. Teenagers were involved in 91 of them. A Politician interested in raising the drivers licenses age claims that one out of every five (p =. 20) auto accidents is due to teenagers. Is there supporting evidence that the proportion is different than this? p = The true proportion of auto accidents involving teenagers. One Proportion H 0: p = 0. 2 z – Test Ha: p ≠ 0. 2 1. SRS – Stated 2. Population of National Auto Accidents ≥ 10(582) 3. 582(. 2) ≥ 10 582(1 -. 2) ≥ 10 Since the P-Value is less than α = 0. 05 the data IS significant. There is strong evidence to REJECT H 0. The Politician is wrong.

14. ) p = The true proportion of mothers who have graduated from college. H 0: p = 0. 31 One Proportion Ha: p ≠ 0. 31 z – Test 1. 2. 3. SRS – NOT Stated Population of mothers ≥ 10(8368) 8368(. 31) ≥ 10 8368(1 -. 31) ≥ 10 Since the P-Value is less than α = 0. 05 the data IS significant. There is strong evidence to REJECT H 0. There is evidence of a change in education level among mothers