Statistical Hypotheses Hypothesis Testing Statistical Hypotheses There are





























- Slides: 35

Statistical Hypotheses & Hypothesis Testing

Statistical Hypotheses There are two types of statistical hypotheses. Null Hypothesis The null hypothesis, denoted by H 0, assumes the sample observations result purely from chance. Alternative Hypothesis The alternative hypothesis, denoted by H 1, states the counter-assumption that sample observations are influenced by some non-random cause. Note: The Alternate Hypothesis is always the logical opposite of the Null Hypothesis. Example: Suppose we wanted to determine whether a coin was fair and balanced. A null hypothesis might be that half the flips would be Heads and half of the flips would be Tails. The alternative hypothesis would be that the number (percent) of Heads and Tails would be very different. Symbolically, these hypotheses would be expressed as: H 0: р = 0. 5 where р = Probability of Heads H 1: р ≠ 0. 5

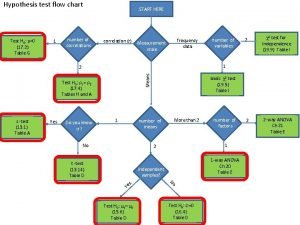
Hypothesis Testing Hypothesis testing is a decision making process about accepting or rejecting a statement (assumption) regarding a population parameter. Frequently, hypothesis testing is applied to a assumption about a population mean. For example, test the assumption that the population mean μ is equal to 120 versus μ is not equal to 120; i. e. , H 0: μ = 120 versus H 1: μ ≠ 120.

References David Harper - Bionic Turtle http: //www. bionicturtle. com/learn/article/type_i_versus_type_ii_errors_9_minute_tutorial/ http: //www. bionicturtle. com/learn/article/hypothesis_testing_9_minute_screencast/ Null and Alternate Hypothesis http: //www. ganesha. org/spc/hyptest. html#hypothesis

Hypothesis Testing

Hypothesis Testing Suppose we believe the average systolic blood pressure of healthy adults is normally distributed with mean μ = 120 and variance σ2 = 50. To test this assumption, we sample the blood pressure of 42 randomly selected adults. Sample statistics are Mean ¿ = 122. 4 Variance s 2 = 50. 3 Standard Deviation s = √ 50. 3 = 7. 09 Standard Error = s / √n = 7. 09 / √ 42 = 1. 09

Central Limit Theorem The distribution of all sample means of sample size n from a Normal Distribution (μ, σ2) is a normally distributed with Mean = μ Variance = σ2 / n For our case: Mean μ = 120 Variance σ2 / n = 50 / 42 = 1. 19 Note: Theoretically we can test the hypothesis regarding the mean and the hypothesis regarding the variance; however one usually presumes the sample variances are stable from sample to sample and any one sample variance is an unbiased estimator of the population variance. As such, hypothesis testing is most frequently associated with testing assumptions regarding the population mean.

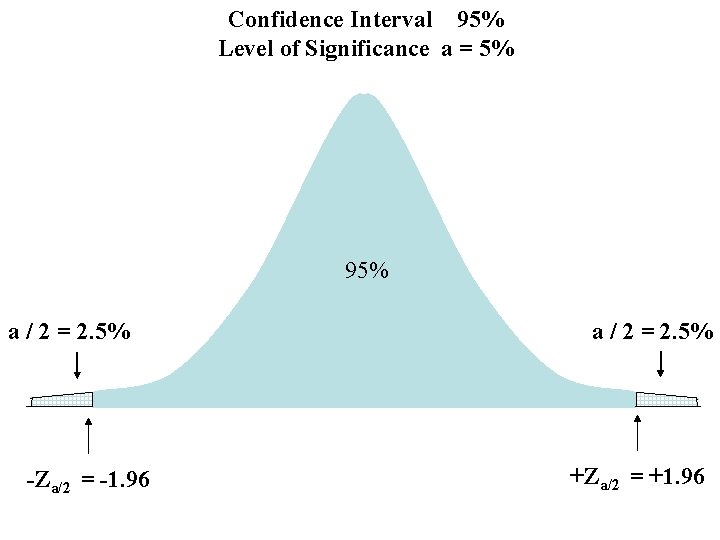
Hypothesis Testing Test the assumption H 0: μ = 120 vs. H 1: μ ≠ 120 using a level of significance α = 5% Note: If our sample came from the assumed population with mean μ = 120, then we would expect 95% of all sample means of sample size n = 42 to be within ± Zα/2 = ± 1. 96

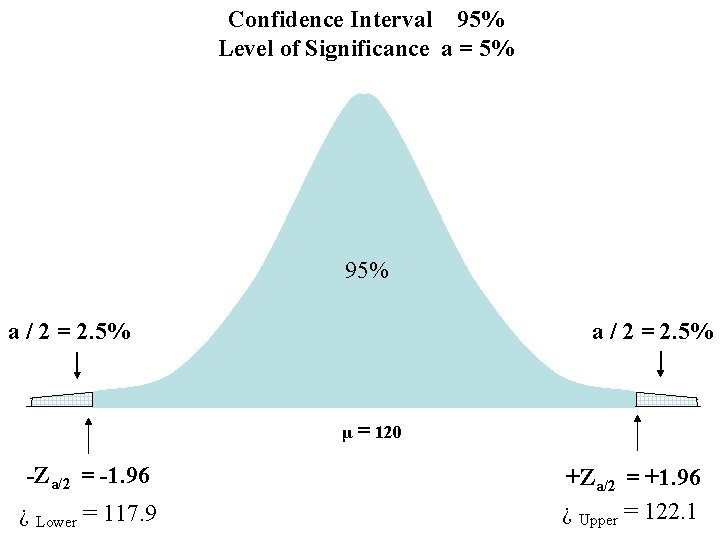
Confidence Interval 95% Level of Significance a = 5% 95% a / 2 = 2. 5% -Za/2 = -1. 96 a / 2 = 2. 5% +Za/2 = +1. 96

Calculate Upper and Lower Bounds on ¿ ¿Lower = μ – Zα/2 (s /√n) = 120 – 1. 96(1. 09) =117. 9 ¿Upper = μ + Zα/2 (s /√n) = 120 + 1. 96(1. 09) =122. 1

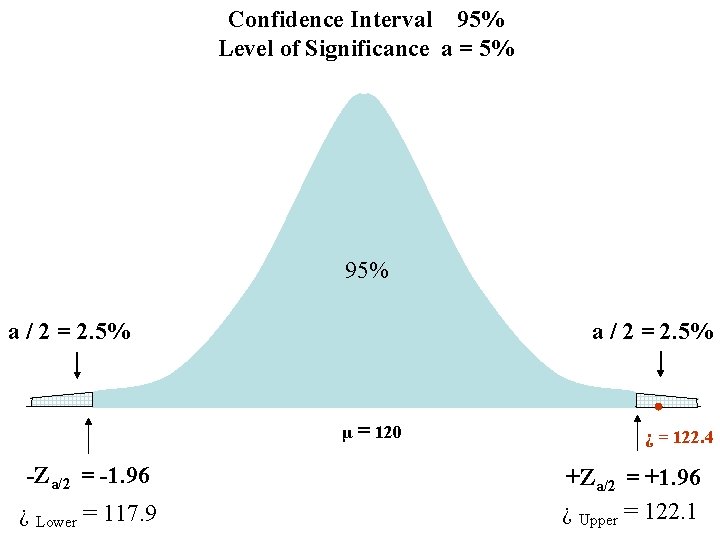
Confidence Interval 95% Level of Significance a = 5% 95% a / 2 = 2. 5% μ = 120 -Za/2 = -1. 96 ¿ Lower = 117. 9 +Za/2 = +1. 96 ¿ Upper = 122. 1

Hypothesis Testing Comparisons Compare our sample mean ¿ = 122. 4 To the Upper and Lower Limits.

Confidence Interval 95% Level of Significance a = 5% 95% a / 2 = 2. 5% μ = 120 -Za/2 = -1. 96 ¿ Lower = 117. 9 ¿ = 122. 4 +Za/2 = +1. 96 ¿ Upper = 122. 1

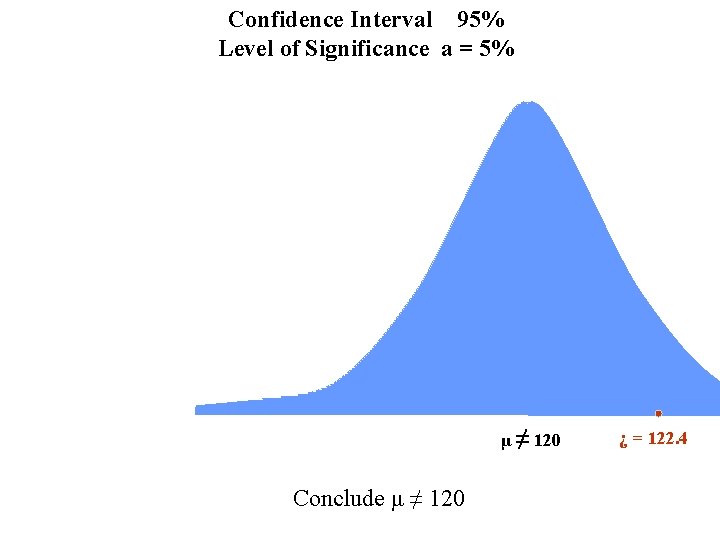
Hypothesis Testing Conclusions Note: Sample mean ¿ = 122. 4 falls outside of the 95% Confidence Interval. We can reach one of two logical conclusions: One, that we expect this to occur for 2. 5% of the samples from a population with mean μ = 120. Two, our sample came from a population with a mean μ ≠ 120. Since 2. 5% = 1/40 is a rather “rare” event; we opt for the conclusion that our original null hypothesis is false and we reject H 0: μ = 120 and therefore accept vs. H 1: μ ≠ 120.

Confidence Interval 95% Level of Significance a = 5% μ ≠ 120 Conclude μ ≠ 120 ¿ = 122. 4

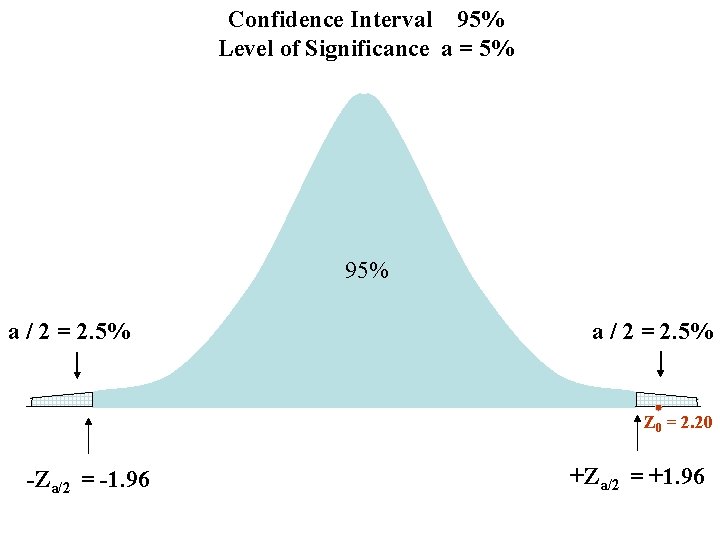
Alternate Method Rather than compare the sample mean to the 95% lower and upper bounds, one can use the Z Transformation for the sample mean and compare the results with ± Zα/2. Z 0 = ( ¿ – μ ) / (s / √n) = (122. 4 – 120) / 1. 09 = 2. 20

Confidence Interval 95% Level of Significance a = 5% 95% a / 2 = 2. 5% Z 0 = 2. 20 -Za/2 = -1. 96 +Za/2 = +1. 96

Alternate Method Note: Since Z 0= 2. 20 value exceeds Zα/2 =1. 96, we reach the same conclusion as before; Reject H 0: μ = 120 and Accept H 1: μ ≠ 120.

Alternate Method - Extended We can quantify the probability (p-Value) of obtaining a test statistic Z 0 at least as large as our sample Z 0. P( |Z 0| > Z ) = 2[1 - Φ (|Z 0|)] p-Value = P( |2. 20| > Z ) = 2[1 - Φ (2. 20)] p-Value = 2(1 – 0. 9861) = 0. 0278 = 2. 8% Compare p-Value to Level of Significance If p-Value < α, then reject null hypothesis Since 2. 8% < 5%, Reject H 0: μ = 120 and conclude μ ≠ 120.

Hypothesis Testing Errors

Hypothesis Testing Suppose we believe the average systolic blood pressure of healthy adults is normally distributed with mean μ = 120 and variance σ2 = 50. To test this assumption, we sample the blood pressure of 42 randomly selected adults. Sample statistics are Mean ¿ = 122. 4 Variance s 2 = 50. 3 Standard Deviation s = √ 50. 3 = 7. 09 Standard Error = s / √n = 7. 09 / √ 42 = 1. 09 Z 0 = ( ¿ – μ ) / (s / √n) = (122. 4 – 120) / 1. 09 = 2. 20

Confidence Interval 95% Level of Significance a = 5% 95% a / 2 = 2. 5% Z 0 = 2. 20 -Za/2 = -1. 96 +Za/2 = +1. 96

Conclusion (Critical Value) Since Z 0= 2. 20 exceeds Zα/2 = 1. 96, Reject H 0: μ = 120 and Accept H 1: μ ≠ 120.

Conclusion (p-Value) We can quantify the probability (p-Value) of obtaining a test statistic Z 0 at least as large as our sample Z 0. P( |Z 0| > Z ) = 2[1 - Φ (|Z 0|)] p-Value = P( |2. 20| > Z ) = 2[1 - Φ (2. 20)] p-Value = 2(1 – 0. 9861) = 0. 0278 = 2. 8% Compare p-Value to Level of Significance If p-Value < α, then reject null hypothesis Since 2. 8% < 5%, Reject H 0: μ = 120 and conclude μ ≠ 120.

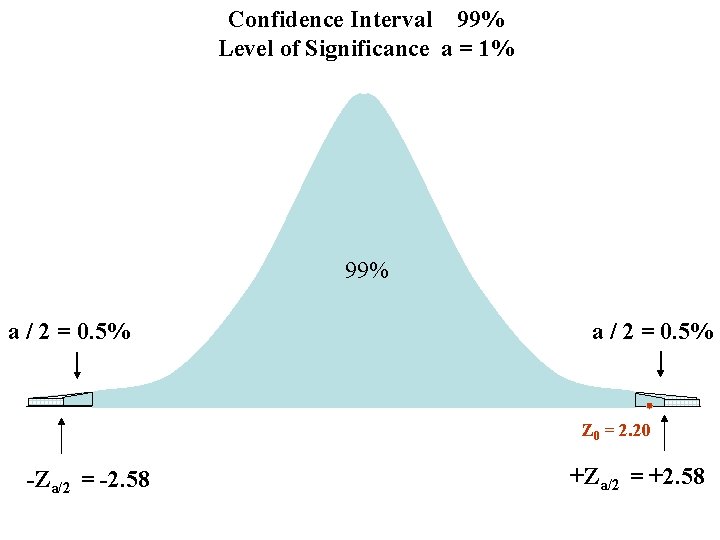
Confidence Interval = 99% Level of Significance α = 1% Z 0 = ( ¿ – μ ) / (s / √n) = (122. 4 – 120) / 1. 09 = 2. 20 Zα/2 = +2. 58

Confidence Interval 99% Level of Significance a = 1% 99% a / 2 = 0. 5% Z 0 = 2. 20 -Za/2 = -2. 58 +Za/2 = +2. 58

Conclusion (Critical Value) Since Z 0= 2. 20 is less than Zα/2 =2. 58, Fail to Reject H 0: μ = 120 and conclude there is insufficient evidence to say H 1: μ ≠ 120.

Conclusion (p-Value) We can quantify the probability (p-Value) of obtaining a test statistic Z 0 at least as large as our sample Z 0. P( |Z 0| > Z ) = 2[1 - Φ (|Z 0|)] p-Value = P( |2. 20| > Z ) = 2[1 - Φ (2. 20)] p-Value = 2(1 – 0. 9861) = 0. 0278 = 2. 8% Compare p-Value to Level of Significance If p-Value < α, then reject null hypothesis Since 2. 8% > 1%, Fail to Reject H 0: μ = 120 and conclude there is insufficient evidence to say H 1: μ ≠ 120.

Hypothesis Testing Conclusions As can be seen in the previous example, our conclusions regarding the null and alternate hypotheses are dependent upon the sample data and the level of significance. Given different values of sample mean and the sample variance or given a different level of significance, we may come to a different conclusion.

Null Hypotheses And Alternate Hypotheses

Hypothesis Testing Hypotheses are always about the population and never about the sample. The true value of a hypothesis can never be known or confirmed. Conclusions regarding hypotheses are never absolute and as such are susceptible to some degree of definable/calculable risk of error. Type I Error Type II Error Rejecting H 0 when H 0 is True Failing to Reject H 0 when H 0 is False Probability of Type I Error = α Probability of Type II Error = β

Power of the Test Probability of Correctly Rejecting a False Null Hypothesis = 1 - β Probability of Correctly Rejecting H 0 when H 1 is true = 1 - β Probability of Rejecting H 0 when H 0 is False = 1 - β Probability of Accepting H 1 when H 1 is True = 1 - β

Probability of Type I and Type II Errors The Level of Significance α establishes the Probability of a Type I Error. The Probability of a Type II Error depends on the magnitude of the true mean and the sample size.

Probability of Type II Errors Consider H 0: μ = μ 0 H 1: μ ≠ μ 0 Suppose the null hypothesis is false and the true magnitude of the mean is μ = μ 0 + δ. and therefore , that is to say Z 0 is normally distributed with mean and variance 1.

Probability of Type II Error Applied Statistics and Probability for Engineers, 3 ed, Montgomery & Runger, Wiley 2003
 Mikael ferm
Mikael ferm Hypothesis stats
Hypothesis stats Chapter 20 testing hypotheses about proportions
Chapter 20 testing hypotheses about proportions Chapter 19 testing hypotheses about proportions
Chapter 19 testing hypotheses about proportions Marzano high yield instructional strategies
Marzano high yield instructional strategies It is an assertion concerning one or more population
It is an assertion concerning one or more population Chapter 20 testing hypotheses about proportions
Chapter 20 testing hypotheses about proportions What is test statistic formula
What is test statistic formula Null hypothesis example
Null hypothesis example What is a null hypothesis
What is a null hypothesis Alternative hypothesis
Alternative hypothesis Null hypothesis statistics
Null hypothesis statistics Nebular hypothesis and protoplanet hypothesis venn diagram
Nebular hypothesis and protoplanet hypothesis venn diagram The language of hypothesis testing
The language of hypothesis testing P value significant difference
P value significant difference One-way anova hypothesis testing
One-way anova hypothesis testing Hypothesis testing assignment
Hypothesis testing assignment Hypothesis testing
Hypothesis testing Critical value hypothesis testing
Critical value hypothesis testing Null hypothesis assumptions
Null hypothesis assumptions Critical value hypothesis testing
Critical value hypothesis testing Goal of hypothesis testing
Goal of hypothesis testing Difference between type 1 and type 2 error
Difference between type 1 and type 2 error 6 steps of hypothesis testing
6 steps of hypothesis testing What is the claim in hypothesis testing
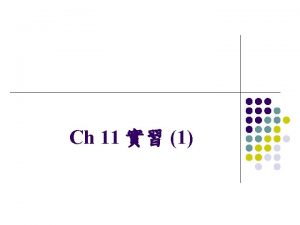
What is the claim in hypothesis testing Psychology statistical test flow chart
Psychology statistical test flow chart Chapter 8 hypothesis testing
Chapter 8 hypothesis testing Chapter 7 hypothesis testing with one sample answers
Chapter 7 hypothesis testing with one sample answers Hypothesis testing for population proportion
Hypothesis testing for population proportion Slope hypothesis testing
Slope hypothesis testing Hypothesis testing business statistics
Hypothesis testing business statistics Edexcel a level maths hypothesis testing
Edexcel a level maths hypothesis testing Manifold hypothesis
Manifold hypothesis Hypothesis testing in r
Hypothesis testing in r Phantoms in statistics
Phantoms in statistics Hypothesis testing in r
Hypothesis testing in r