Hypothesis Testing The goal of hypothesis testing is

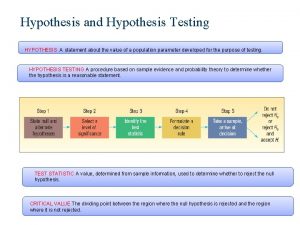
Hypothesis Testing The goal of hypothesis testing is to set up a procedure(s) to allow us to decide if a model is acceptable in light of our experimental observations. Example: A theory predicts that BR(Higgs®m+m -)= 2 x 10 -5 and you measure (4± 2) x 10 -5. The hypothesis we want to test is “are experiment and theory consistent? ” Hypothesis testing does not have to compare theory and experiment. Example: CLEO measures the Lc lifetime to be (180 ± 7)fs while SELEX measures (198 ± 7)fs. The hypothesis we want to test is “are the lifetime results from CLEO and SELEX consistent? ” There are two types of hypotheses tests: parametric and non-parametric Parametric: compares the values of parameters (e. g. does the mass of proton = mass of electron ? ) Non-parametric: deals with the shape of a distribution (e. g. is angular distribution consistent with being flat? ) Consider the case of neutron decay. Suppose we have two theories that both predict the energy spectrum of the electron emitted in the decay of the neutron. Here a parametric test might not be able to distinguish between the two theories since both theories might predict the same average energy of the emitted electron. However a non-parametric test would be able to distinguish between the two theories as the shape of the energy spectrum differs for each theory. 880. P 20 Winter 2006 Richard Kass 1

Hypothesis testing A procedure for using hypothesis testing: a) b) c) Measure (or calculate) something Find something that you wish to compare with your measurement (theory, experiment) Form a hypothesis (e. g. my measurement, x, is consistent with the PDG value) H 0: x=x. PDG H 0 is called the “null hypothesis” d) e) Calculate the confidence level that the hypothesis is true Accept or reject the hypothesis depending on some minimum acceptable confidence level Problems with the above procedure a) b) c) What is a confidence level ? How do you calculate a confidence level? What is an acceptable confidence level ? How would we test the hypothesis “the space shuttle is safe? ” Is 1 explosion per 10 launches safe? Or 1 explosion per 1000 launches? A working definition of the confidence level: The probability of the event happening by chance. Example: Suppose we measure some quantity (X) and we know that it is described by a gaussian pdf with m=0 and s=1. What is the confidence level for measuring X ³ 2 (i. e. ³ 2 s from the mean)? Thus we would say that the confidence level for measuring X ³ 2 is 0. 025 or 2. 5% and we would expect to get a value of X ³ 2 one out of 40 tries if the underlying pdf is gaussian. 880. P 20 Winter 2006 Richard Kass 2

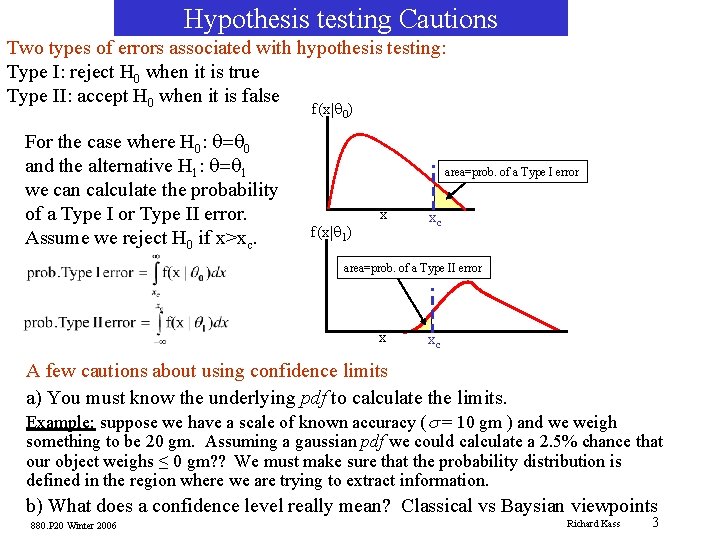
Hypothesis testing Cautions Two types of errors associated with hypothesis testing: Type I: reject H 0 when it is true Type II: accept H 0 when it is false f(x|q 0) For the case where H 0: q=q 0 and the alternative H 1: q=q 1 we can calculate the probability of a Type I or Type II error. Assume we reject H 0 if x>xc. area=prob. of a Type I error f(x|q 1) x xc area=prob. of a Type II error x xc A few cautions about using confidence limits a) You must know the underlying pdf to calculate the limits. Example: suppose we have a scale of known accuracy (s = 10 gm ) and we weigh something to be 20 gm. Assuming a gaussian pdf we could calculate a 2. 5% chance that our object weighs ≤ 0 gm? ? We must make sure that the probability distribution is defined in the region where we are trying to extract information. b) What does a confidence level really mean? Classical vs Baysian viewpoints 880. P 20 Winter 2006 Richard Kass 3

Hypothesis Testing-Gaussian Variables We wish to test if a quantity we have measured (m=average of n measurements ) is consistent with a known mean (m 0). H 0: 0. 9± 0. 2=0. 33 880. P 20 Winter 2006 If acceptable CL=5%, then we would reject H 0 Richard Kass 4

Hypothesis Testing-Gaussian Variables Do charge 2/3 quarks exist? H 0: 0. 9± 0. 2=0. 67 If acceptable CL=5%, then we would accept H 0 Another variation of the quark problem H 0: our charge measurements are consistent with q=1/3 quarks If acceptable CL=5%, then we would reject H 0 880. P 20 Winter 2006 Richard Kass 5

Hypothesis Testing-Gaussian Variables Tests when both means are unknown but come from a gaussian pdf: n and m are the number of measurements for each mean Example: Do two experiments agree with each other? CLEO measures the Lc lifetime to be (180 ± 7)fs while SELEX measures (198 ± 7)fs. H 0: 180± 7=198 ± 7 Thus 7% of the time we should expect the experiments to disagree at this level. If acceptable CL=5%, then we would accept H 0 880. P 20 Winter 2006 Richard Kass 6

Hypothesis Testing-non-Gaussian Variables Assume we have a bunch of measurements (xi’s) that are NOT from a gaussian pdf. (e. g. they could be from a poisson distribution) We can calculate a quantity that looks like a c 2 which compares our data (di) with corresponding predictions (PR(xi)) from a pdf: K. Pearson showed that for a wide variety of pdfs (e. g. Poisson) the above test statistic becomes distributed according to a c 2 pdf with n-1 dof. For example, the data are from a poisson distribution with mean=m. If we have a total of N events in our sample then we predict: NP(m, m) events for a given value of m (= 0, 1, 2, 3, 4…. ) At the same time, we have observed N(m) events. If NP(m, m) >5 for all m then the following is approximately a c 2 with n-1 dof. 880. P 20 Winter 2006 Richard Kass 7

Hypothesis Testing-Pearson’s c 2 Test The following is the numbers of neutrino events detected in 10 second intervals by the IMB experiment on 23 February 1987 around which time the supernova S 1987 a was first seen by experimenters: #events 0 1 2 3 4 5 6 7 8 9 #intervals 1024 860 307 58 15 3 0 0 0 1 Assuming the data is described by a Poisson distribution. Calculate the average & compute the average number events expected in an interval. l= 0. 777 if we include interval with 9 events We can calculate a c 2 assuming the data are described by a Poisson distribution: The predicted number of intervals is given by: Note: we use s 2=prediction for a Poisson #events 0 1 2 3 4 5 6 7 8 9 #intervals predicted 1064 823 318 82 16 2 0. 3 0. 003 0. 0003 There are 7 (= 9 -2) DOF’s here and the probability of c 2/D. O. F. = 3. 6/7 is high (≈80%), indicating a good fit to a Poisson Reject H 0: “interval with 9 events is from Poisson with l=0. 77” 880. P 20 Winter 2006 Richard Kass 8