HMM Hidden Markov Models Xuhua Xia xxiauottawa ca

HMM (Hidden Markov Models) Xuhua Xia xxia@uottawa. ca http: //dambe. bio. uottawa. ca

Infer the invisible • In science, one often needs to infer what is not visible based on what is visible. • Examples in this lecture – Detecting missing alleles in a locus – Hidden Markov model (the main topic) Xuhua Xia Slide 2

Detecting missing alleles in a locus Suppose we obtain 30 individuals with a single A band, 30 with a single B band, and 40 individuals with both A and B bands (NA? = 30, NB? = 30, NAB = 40). With H 2 (hypothesis of two alleles) which assumes NA? = NAA and NB? = NBB, the proportion of AA, AB and BB genotype are p. A 2, 2 p. Ap. B, and p. B 2, respectively. So, assuming H-W equilibrium, the loglikelihood function for estimating p. A is A B which will lead to p. A = 0. 5, and ln. LH 2 = -110. 90355. We do not need to estimate pa because pa = 1 – p. A. With H 3 (3 alleles, with a 3 rd cryptic allele C) we need to estimate p. A and p. B. The log-likelihood function is which will lead to p. A = p. B = 0. 4667 (and p. C = 0. 0666), and ln. LH 3 = -109. 62326. LRT or information-theoretic indices, e. g.

Markov Models • A model of a stochastic process over time or space • Components of a Markov model – A set of states – A set of dependence – A set of transition probabilities • Examples: – Markov chain of nucleotide (or amino acid) substitutions over time – Markov models of site dependence Xuhua Xia Slide 4

Morkov models over 1 -dimention • S = RRRYYYRRRYYY……, • 0 -order Markov model R – PR = 0. 5 – PY = 0. 5 – What is the nucleotide at site i? • Site dependence • 1 st-order Markov model – PRR = PYY = 2/3 – PYR = PRY =1/3 – P(Si|Si-1 = R)? • 2 nd-order Markov model Y R Y 2/3 1/3 2/3 3 1 R Y 2 R Y R 1/6 0 1/6 – P(Si|Si-2 = R, Si-1 = Y)? • 3 rd-order and higher order Markov models: rarely used Xuhua Xia Slide 5 Y 1/6 0 1/6

Long-range dependence Xuhua Xia Slide 6

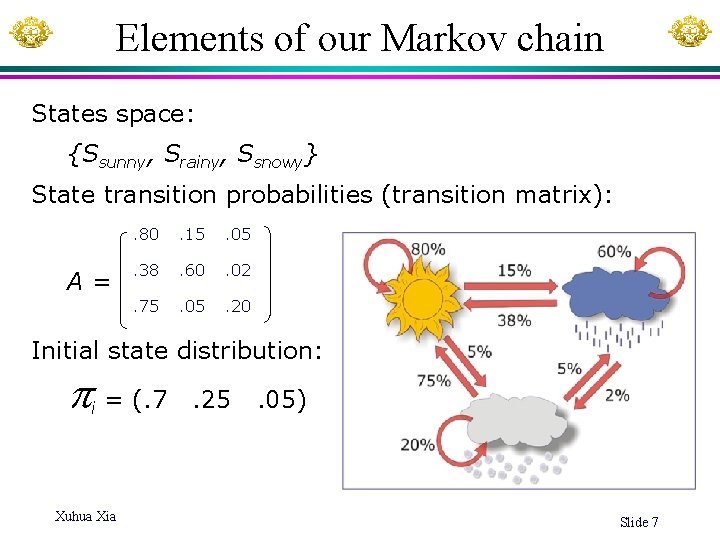
Elements of our Markov chain States space: {Ssunny, Srainy, Ssnowy} State transition probabilities (transition matrix): A= . 80 . 15 . 05 . 38 . 60 . 02 . 75 . 05 . 20 Initial state distribution: = (. 7 i Xuhua Xia . 25 . 05) Slide 7

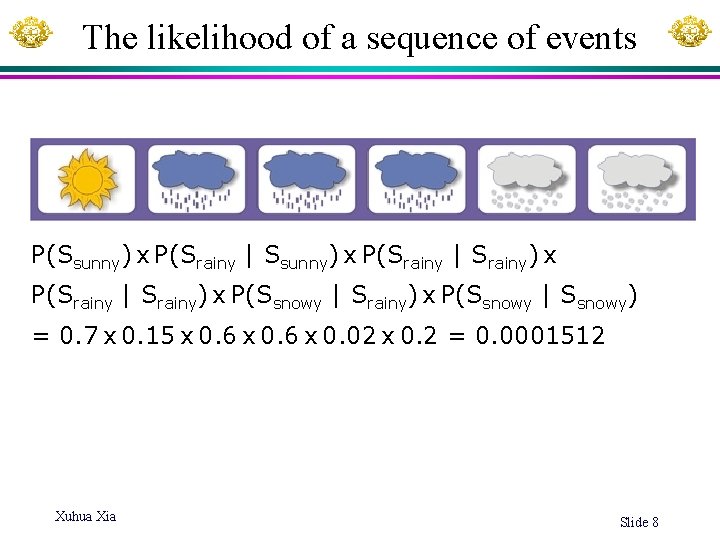
The likelihood of a sequence of events P(Ssunny) x P(Srainy | Srainy) x P(Ssnowy | Ssnowy) = 0. 7 x 0. 15 x 0. 6 x 0. 02 x 0. 2 = 0. 0001512 Xuhua Xia Slide 8

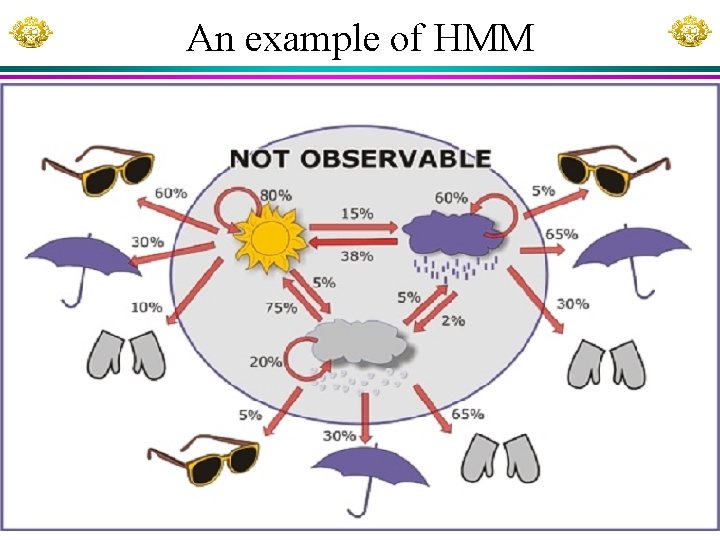
An example of HMM Xuhua Xia Slide 9

HMM: A classic example Dishonest casino dealer secretly switching between 1. a fair (F) die with P(i, i=1 to 6) = 1/6 and 2. a loaded (L) die with P(6) = 1 Is it possible to know how many dice the dishonest casino dealer uses? Need specific hypotheses: e. g. , Visible: 1354634255112466666122363 Hidden: FFFFFFFLLLLLFFFFFF F L 1 2 3 4 5 6 F PFL 1/6 1/6 1/6 L PLF PLL 0 0 0 1 H 1: he has two H 2: he has three HMM: 1. State space: {S 1, S 2, …, SN} 2. State transition probabilities (transition matrix): aij = P(Si, t+1 | Sj, t) 3. Observations: {O 1, O 2, …, OM} 4. Emission probabilities: bj(k) = P(Ok| Sj) Xuhua Xia Is it possible to reconstruct the hidden Markov model and infer all hidden states? Almost never. Success of inference depends mainly on 1) differences in emission probabilities, and 2) how long the chain will stay in each state

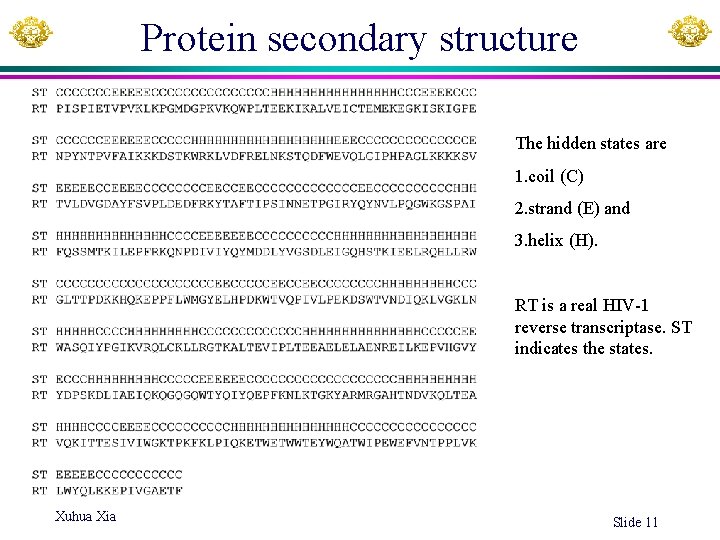
Protein secondary structure The hidden states are 1. coil (C) 2. strand (E) and 3. helix (H). RT is a real HIV-1 reverse transcriptase. ST indicates the states. Xuhua Xia Slide 11

Transition probabilities over sites C E H C 0. 88210 0. 06987 0. 04803 E 0. 26154 0. 73846 0. 00000 H 0. 06897 0. 00690 0. 92414 The relatively large values in the diagonal are typical of Markov chains where a state tends to stay in the same state for several consecutive observations (amino acids in our case). Quality of inference increases with the diagonal values. Xuhua Xia Slide 12

Emission probabilities AA C E H A 0. 0262 0. 0308 0. 0552 C 0. 0000 0. 0138 D 0. 0568 0. 0154 0. 0345 E 0. 0742 0. 0308 0. 1379 F 0. 0218 0. 0462 0. 0276 G 0. 0961 0. 0000 0. 0138 H 0. 0218 0. 0000 0. 0138 I 0. 0480 0. 1385 0. 0828 K 0. 1135 0. 0769 0. 1172 L 0. 0699 0. 0769 0. 1103 M 0. 0131 0. 0154 0. 0138 N 0. 0393 0. 0000 0. 0276 P 0. 1397 0. 0154 0. 0138 Q 0. 0393 0. 0769 0. 0828 R 0. 0218 0. 0000 0. 0621 S 0. 0393 0. 0308 0. 0207 T 0. 0830 0. 0615 0. 0621 V 0. 0393 0. 1846 0. 0483 W 0. 0306 0. 0462 0. 0552 Xuhua Xia Y 0. 0262 0. 1539 0. 0069 Quality of inferring the hidden states increases with the difference in emission probabilities. Predicting secondary structure based only on emission probabilities only: 12345678901 T = YVYVEEEEEEPGPG Naïve = EEEEHHHHHHCCCC PEH in the transition probability matrix is 0. 00000, implying an extremely small probability of E followed by H. Our naïve prediction above with an H at position 5 (following an E at position 4) therefore represents an extremely unlikely event. Another example is at position 11 with T 11 = V. Our prediction of Naïve 11 = E implies a transition of secondary structure from H to E (Naïve 10 and Naïve 11) and then back from E to H (Naïve 11 and Naïve 12). The transition probability matrix shows us that PHE and PEH are both very small. So S 11 is very unlikely to be E.

Infer the hidden states: Viterbi algorithm • A dynamic programming algorithm • Incorporate information from both the transition probability matrix and the emission probability matrix • Need two matrices – Viterbi matrix (Vij): log-likelihood of state j at position i. – Backtrack matrix (B) – Both of dimension Num. State × Seq. Len • Output: a reconstructed hidden state sequence • Example: predicting secondary structure of sequence YVYVEEEEEEPGPG Xuhua Xia Slide 14

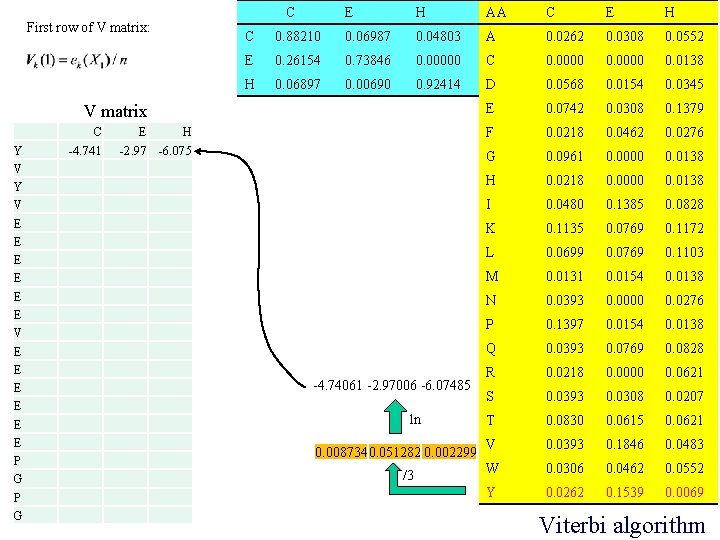
First row of V matrix: C E H AA C E H C 0. 88210 0. 06987 0. 04803 A 0. 0262 0. 0308 0. 0552 E 0. 26154 0. 73846 0. 00000 C 0. 0000 0. 0138 H 0. 06897 0. 00690 0. 92414 D 0. 0568 0. 0154 0. 0345 E 0. 0742 0. 0308 0. 1379 F 0. 0218 0. 0462 0. 0276 G 0. 0961 0. 0000 0. 0138 H 0. 0218 0. 0000 0. 0138 I 0. 0480 0. 1385 0. 0828 K 0. 1135 0. 0769 0. 1172 L 0. 0699 0. 0769 0. 1103 M 0. 0131 0. 0154 0. 0138 N 0. 0393 0. 0000 0. 0276 P 0. 1397 0. 0154 0. 0138 Q 0. 0393 0. 0769 0. 0828 R 0. 0218 0. 0000 0. 0621 S 0. 0393 0. 0308 0. 0207 T 0. 0830 0. 0615 0. 0621 V 0. 0393 0. 1846 0. 0483 W 0. 0306 0. 0462 0. 0552 Y 0. 0262 0. 1539 0. 0069 V matrix Y V E E E P G C -4. 741 E H -2. 97 -6. 075 -4. 74061 -2. 97006 -6. 07485 ln 0. 0087340. 051282 0. 002299 /3 Viterbi algorithm

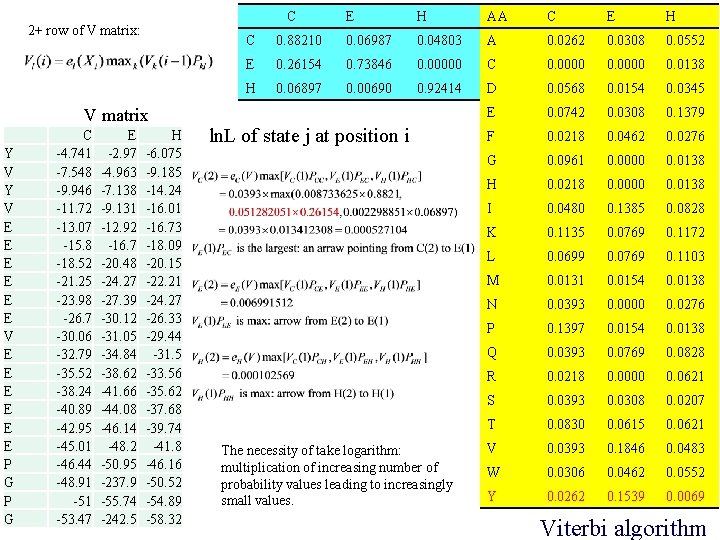
C 2+ row of V matrix: V matrix Y V E E E P G C -4. 741 -7. 548 -9. 946 -11. 72 -13. 07 -15. 8 -18. 52 -21. 25 -23. 98 -26. 7 -30. 06 -32. 79 -35. 52 -38. 24 -40. 89 -42. 95 -45. 01 -46. 44 -48. 91 -53. 47 E -2. 97 -4. 963 -7. 138 -9. 131 -12. 92 -16. 7 -20. 48 -24. 27 -27. 39 -30. 12 -31. 05 -34. 84 -38. 62 -41. 66 -44. 08 -46. 14 -48. 2 -50. 95 -237. 9 -55. 74 -242. 5 H -6. 075 -9. 185 -14. 24 -16. 01 -16. 73 -18. 09 -20. 15 -22. 21 -24. 27 -26. 33 -29. 44 -31. 5 -33. 56 -35. 62 -37. 68 -39. 74 -41. 8 -46. 16 -50. 52 -54. 89 -58. 32 E H AA C E H C 0. 88210 0. 06987 0. 04803 A 0. 0262 0. 0308 0. 0552 E 0. 26154 0. 73846 0. 00000 C 0. 0000 0. 0138 H 0. 06897 0. 00690 0. 92414 D 0. 0568 0. 0154 0. 0345 E 0. 0742 0. 0308 0. 1379 F 0. 0218 0. 0462 0. 0276 G 0. 0961 0. 0000 0. 0138 H 0. 0218 0. 0000 0. 0138 I 0. 0480 0. 1385 0. 0828 K 0. 1135 0. 0769 0. 1172 L 0. 0699 0. 0769 0. 1103 M 0. 0131 0. 0154 0. 0138 N 0. 0393 0. 0000 0. 0276 P 0. 1397 0. 0154 0. 0138 Q 0. 0393 0. 0769 0. 0828 R 0. 0218 0. 0000 0. 0621 S 0. 0393 0. 0308 0. 0207 T 0. 0830 0. 0615 0. 0621 V 0. 0393 0. 1846 0. 0483 W 0. 0306 0. 0462 0. 0552 Y 0. 0262 0. 1539 0. 0069 ln. L of state j at position i The necessity of take logarithm: multiplication of increasing number of probability values leading to increasingly small values. Viterbi algorithm

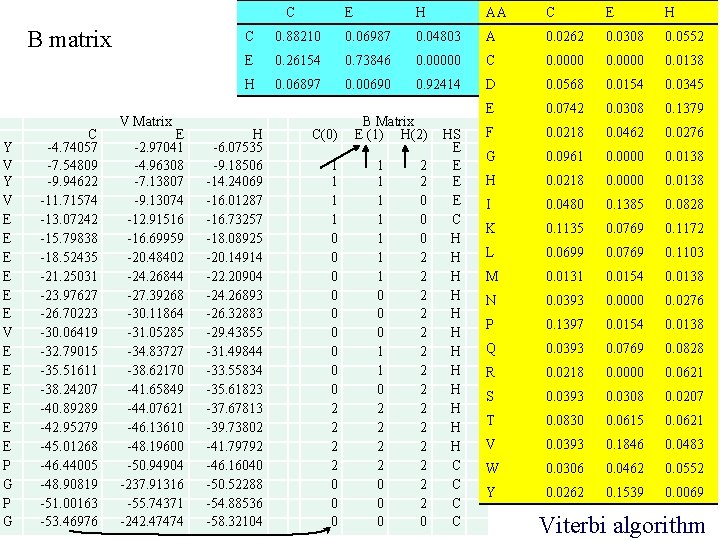
C B matrix Y V E E E P G C -4. 74057 -7. 54809 -9. 94622 -11. 71574 -13. 07242 -15. 79838 -18. 52435 -21. 25031 -23. 97627 -26. 70223 -30. 06419 -32. 79015 -35. 51611 -38. 24207 -40. 89289 -42. 95279 -45. 01268 -46. 44005 -48. 90819 -51. 00163 -53. 46976 V Matrix E -2. 97041 -4. 96308 -7. 13807 -9. 13074 -12. 91516 -16. 69959 -20. 48402 -24. 26844 -27. 39268 -30. 11864 -31. 05285 -34. 83727 -38. 62170 -41. 65849 -44. 07621 -46. 13610 -48. 19600 -50. 94904 -237. 91316 -55. 74371 -242. 47474 E H AA C E H C 0. 88210 0. 06987 0. 04803 A 0. 0262 0. 0308 0. 0552 E 0. 26154 0. 73846 0. 00000 C 0. 0000 0. 0138 H 0. 06897 0. 00690 0. 92414 D 0. 0568 0. 0154 0. 0345 E 0. 0742 0. 0308 0. 1379 F 0. 0218 0. 0462 0. 0276 G 0. 0961 0. 0000 0. 0138 H 0. 0218 0. 0000 0. 0138 I 0. 0480 0. 1385 0. 0828 K 0. 1135 0. 0769 0. 1172 L 0. 0699 0. 0769 0. 1103 M 0. 0131 0. 0154 0. 0138 N 0. 0393 0. 0000 0. 0276 P 0. 1397 0. 0154 0. 0138 Q 0. 0393 0. 0769 0. 0828 R 0. 0218 0. 0000 0. 0621 S 0. 0393 0. 0308 0. 0207 T 0. 0830 0. 0615 0. 0621 V 0. 0393 0. 1846 0. 0483 W 0. 0306 0. 0462 0. 0552 Y 0. 0262 0. 1539 0. 0069 H -6. 07535 -9. 18506 -14. 24069 -16. 01287 -16. 73257 -18. 08925 -20. 14914 -22. 20904 -24. 26893 -26. 32883 -29. 43855 -31. 49844 -33. 55834 -35. 61823 -37. 67813 -39. 73802 -41. 79792 -46. 16040 -50. 52288 -54. 88536 -58. 32104 C(0) 1 1 0 0 0 0 0 2 2 0 0 0 B Matrix E (1) H(2) 1 1 1 1 0 0 0 1 1 0 2 2 0 0 0 2 2 2 2 0 HS E E C H H H C C Viterbi algorithm

The Viterbi Algorithm • Dynamic programming algorithm – Score matrix V – Backtrack matrix B C E H C 0. 88210 0. 06987 0. 04803 E 0. 26154 0. 73846 0. 00000 H 0. 06897 0. 00690 0. 92414 12345678901 T = YVYVEEEEEEPGPG Viterbi = EEEECHHHHHHCCCC Naïve = EEEEHHHHHHCCCC Xuhua Xia Slide 18

Objectives and computation in HMM • Define the model structure, e. g. , number of hidden states, number of observed events • Obtain training data • Training HMM to obtain transition probability matrix and emission probabilities • Viterbi algorithm to reconstruct the hidden states • Forward algorithm to compute the probability of the observed sequence • Utility again: – Better understanding – Better prediction Xuhua Xia Slide 19