Heavy ion collisions and Ad SCFT Amos Yarom

Heavy ion collisions and Ad. S/CFT Amos Yarom With S. Gubser and S. Pufu.

Part 2: Entropy estimates

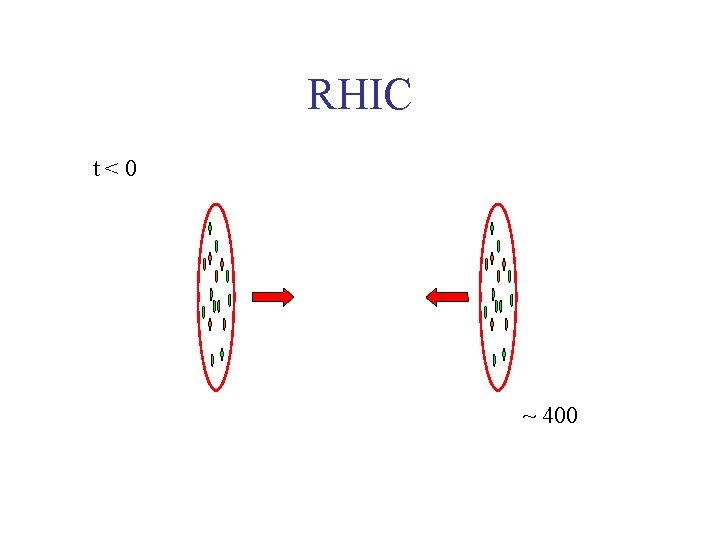
RHIC t<0 ~ 400

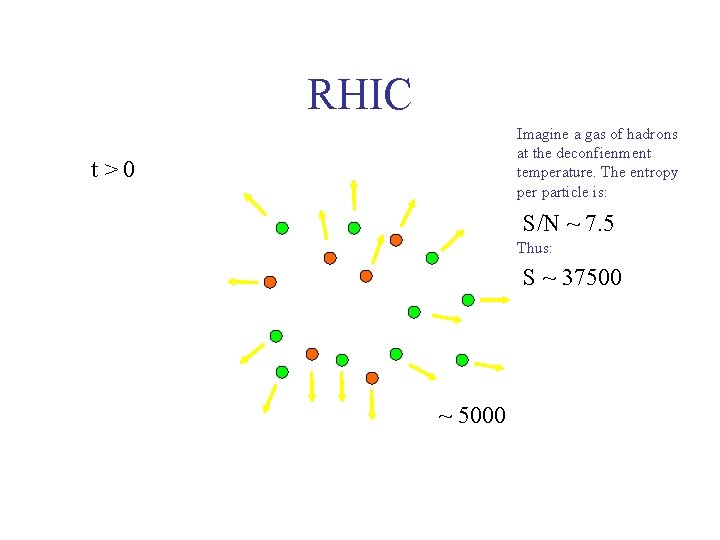
RHIC Imagine a gas of hadrons at the deconfienment temperature. The entropy per particle is: t>0 S/N ~ 7. 5 Thus: S ~ 37500 ~ 5000

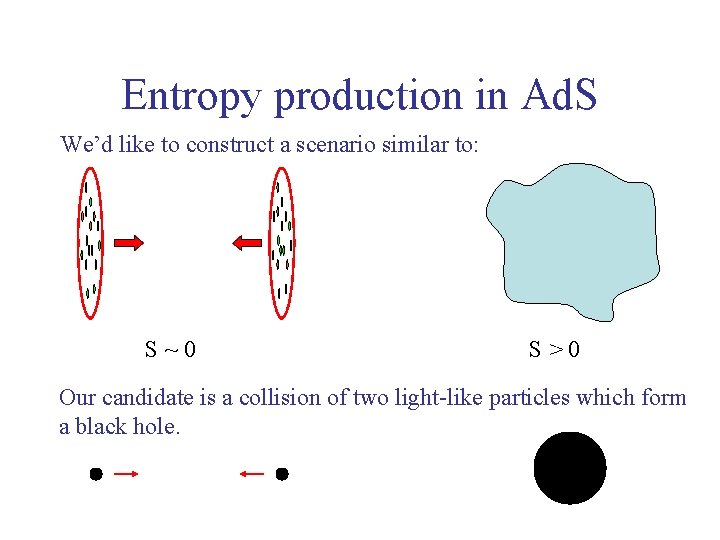
Entropy production in Ad. S We’d like to construct a scenario similar to: S~0 S>0 Our candidate is a collision of two light-like particles which form a black hole.

Light-like particles in Ad. S 0 z=z* z

Light-like particles in Ad. S 0 z=z* z

Light-like particles in Ad. S Equations of motion for the metric: Let’s switch to light-like coordinates: Then: Stress tensor of a light-like particle.

Light-like particles in Ad. S Equations of motion for the metric: Let’s switch to light-like coordinates: Then: We use an ansatz:

Light-like particles in Ad. S The equations of motion for the metric: with the ansatz: reduce to:

Light-like particles in Ad. S The solution to: is: where:

Light-like particles in Ad. S 0 z=z* z

Light-like particles in Ad. S 0 z=z* z

Light-like particles in Ad. S z=z* t The line element we wrote down is a solution anywhere outside the future light-cone of the collision point. t=0 x 3 x 1, x 2

Horizons Event horizon: boundary of causal curves reaching future null infinity. Marginally trapped surface: ~ a 3 dimensional surface for which the outward pointing null vector propagates neither inward nor outward and the other propagates inward. be the null normal vectors to the surface. Let: and Then, a marginally trapped surface satisfies:

Horizons A trapped surface is always on or inside an event horizon. The area of the event horizon can only increase The entropy of a black hole is proportional to its area Goal: Find a marginally trapped surface, compute its area, and obtain a lower bound on the entropy of the black hole.

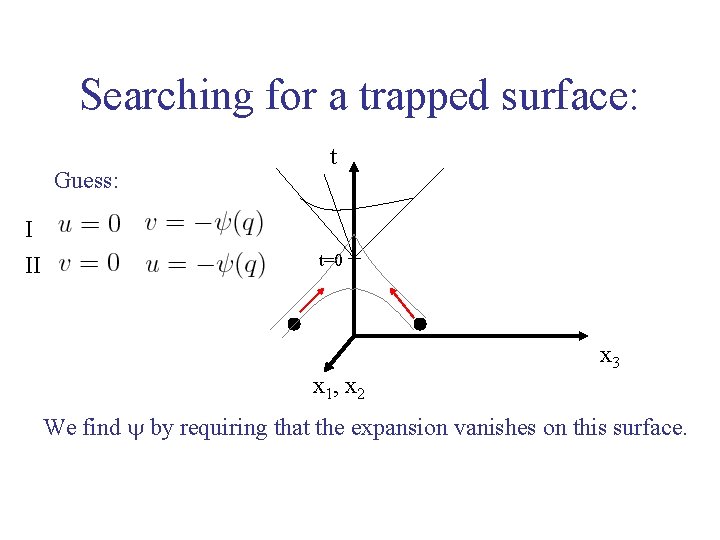
Searching for a trapped surface: Guess: t I II t=0 x 3 x 1, x 2 We find y by requiring that the expansion vanishes on this surface.

Searching for a trapped surface: Guess: I II We find y by requiring that the expansion vanishes on this surface. A normal to the surface is given by: The metric is singular at u=0 and ! v<0. In order for the metric to be finite we use the coordinate transformation: Requiring that it’s light-like, outward pointing and future directing,

Searching for a trapped surface: Guess: I II We find y by requiring that the expansion vanishes on this surface. A normal to the surface is given by: The inward pointing null vector is given by:

Searching for a trapped surface: Guess: I II We find y by requiring that the expansion vanishes on this surface. The normals to the surface are given by: From symmetry:

Searching for a trapped surface: Guess: I II The normal to the surface is: The induced metric should be orthogonal to the normals. To find it, we make the guess: and determine A, B and C though:

Searching for a trapped surface: Guess: I II With and we can compute the expansion: After some work, we find (using With the boundary conditions: ):

Searching for a trapped surface: We need to solve: With the boundary conditions: The most general, non-singular, solution to the differential equation is: We denote the boundary by the surface q=qc. Then, the boundary conditions turn into algebraic relations between qc and K:

Searching for a trapped surface: We found a trapped surface: I II Where: with

Horizons A trapped surface is always on or inside an event horizon. The area of the event horizon can only increase The entropy of a black hole is proportional to its area Goal: Find a marginally trapped surface, compute its area, and obtain a lower bound on the entropy of the black hole.

Searching for a trapped surface: We found a trapped surface: I II Where: with The area is given by:

Searching for a trapped surface: We found a trapped surface: I II Its area is: The lower bound on the entropy is:

Converting to boundary quantities Let’s see what the collision looks like on the boundary. Recall that: So from:

Converting to boundary quantities Let’s see what the collision looks like on the boundary. Recall that: From the form of the metric we find: So we convert: E=Ebeam=19. 7 Te. V z*=4. 3 fm

Converting to boundary quantities We convert: E = Ebeam = 19. 7 Te. V Naively: Recall z* = 4. 3 fm But more generally:

Converting to boundary quantities We convert: E = Ebeam = 19. 7 Te. V Naively: Compare: z* = 4. 3 fm But more generally:

Converting to boundary quantities We convert: E = Ebeam = 19. 7 Te. V So that: z* = 4. 3 fm

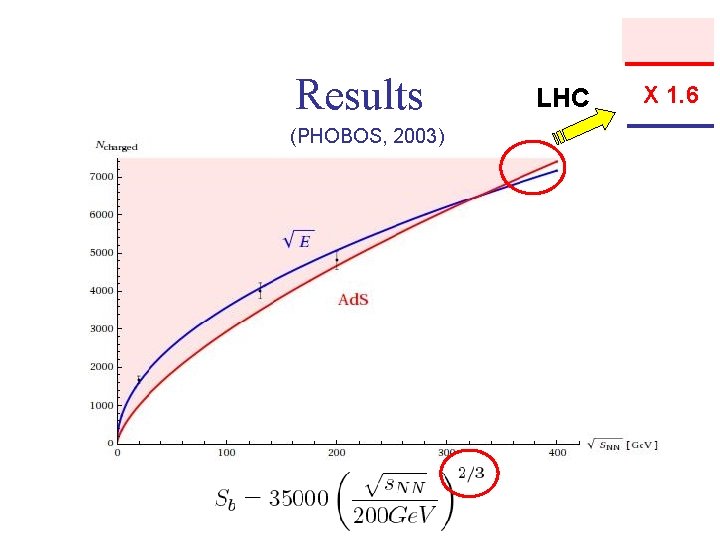
Results (PHOBOS, 2003) LHC X 1. 6

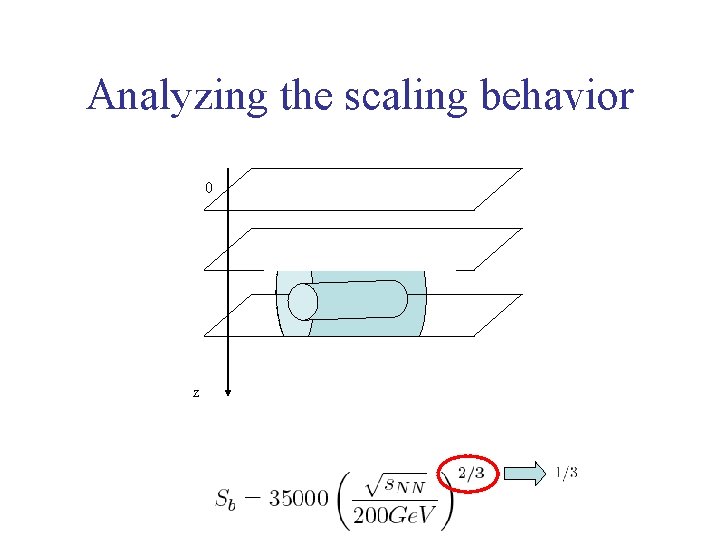
Analyzing the scaling behavior 0 z

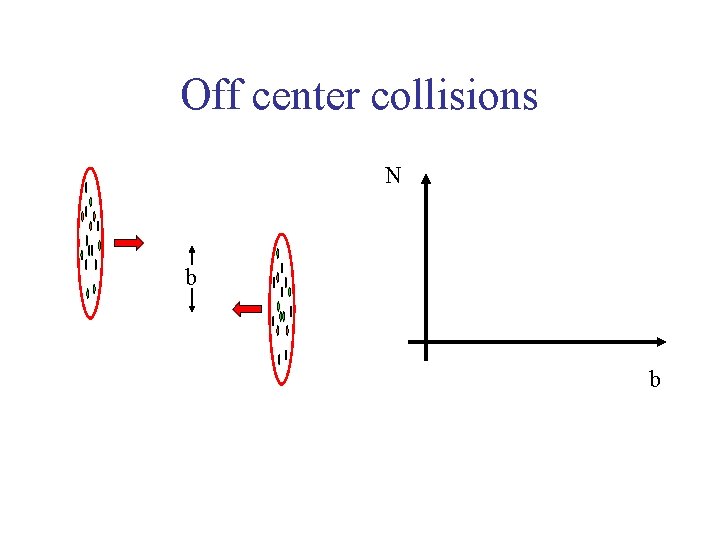
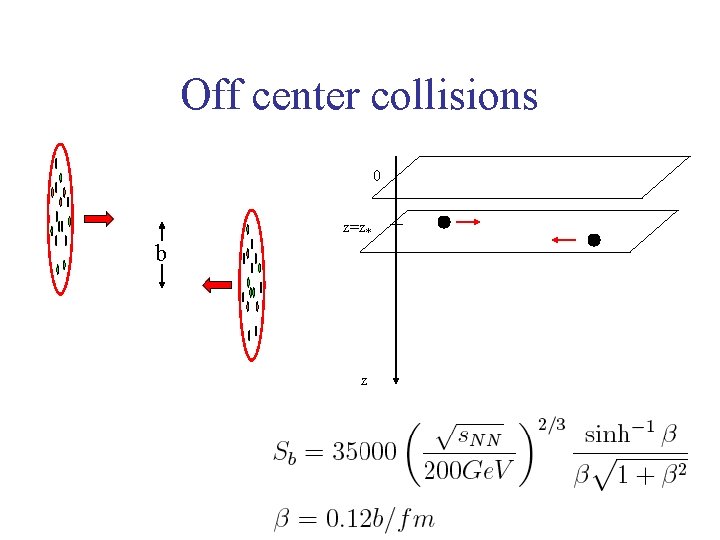
Off center collisions N b b

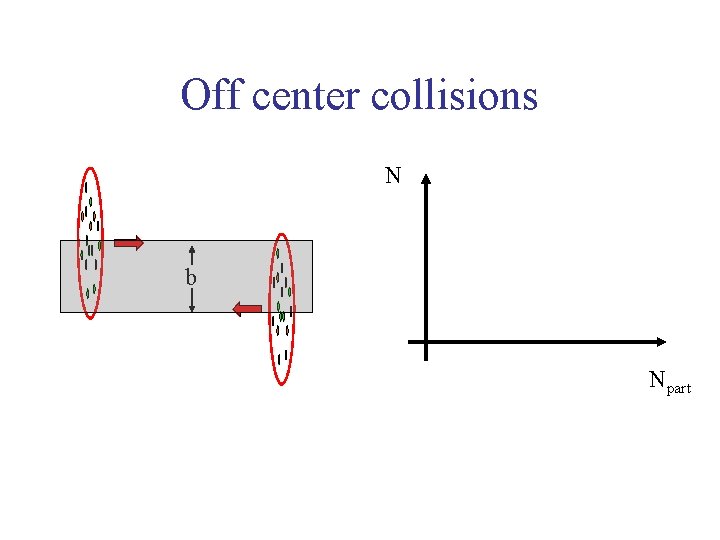
Off center collisions N b Npart

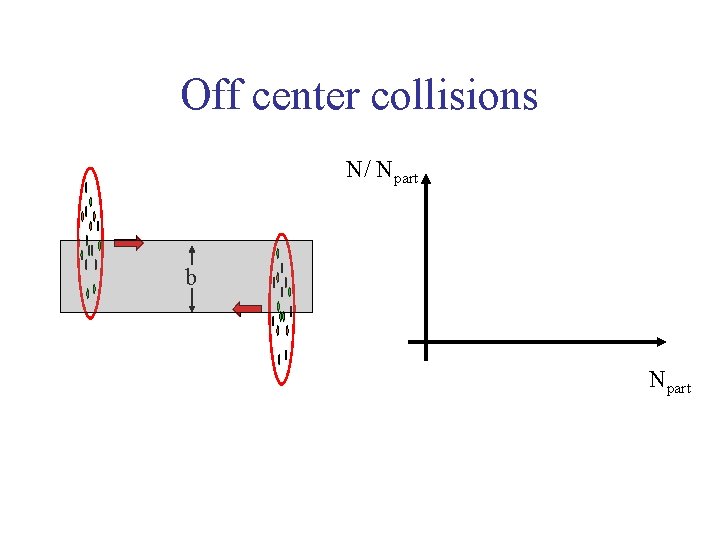
Off center collisions N/ Npart b Npart

Off center collisions

Off center collisions 0 z=z* b z

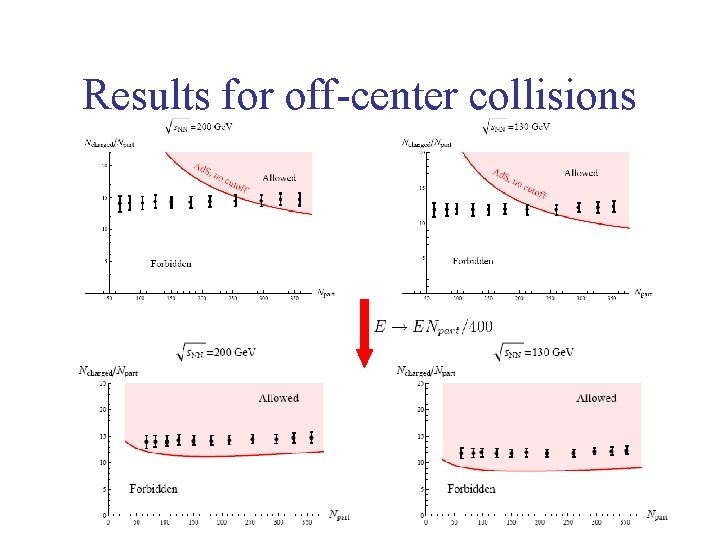
Results for off-center collisions

Results for off-center collisions “spectators” In a confining theory the spectators don’t participate in the collisions. b For the purpose of this calculation we can “mimic” confinenemnt by setting:

Results for off-center collisions

References • • • PHOBOS collaboration nucl-ex/0410022. Multiplicity data. Aichelburg and Sexl. Gen. Rel. Grav. 2 (1972) 303 -312 Shock wave geometries in flat space. Hotta et. al. Class. Quant. Grav. 10 (1993) 307 -314, Stefsos et. al. hep-th/9408169, Podolsky et. al. gr-qc/9710049, Horowitz et. al. hep-th/9901012, Emparan hep-th/0104009, Kang et. al. hepth/0410173. Shock wave geometries in Ad. S space. Penrose, unpublished, Eardley and Giddings, gr-qc/0201034, Yoshino et. al. gr-qc/0209003 Trapped surface computation in flat space. Gubser et. al. 0805. 1551, Lin et. al 0902. 1508, Gubser et. al. 0902. 4062 Trapped surface computation in Ad. S space.