Gated Graphs and Causal Inference John Winn Microsoft








![do calculus • [Pearl, Causal diagrams for empirical research, Biometrika 1995] do calculus • [Pearl, Causal diagrams for empirical research, Biometrika 1995]](https://slidetodoc.com/presentation_image/5ead5f2b2a3df7537ef9c00ae8026eb3/image-32.jpg)





- Slides: 51

Gated Graphs and Causal Inference John Winn Microsoft Research, Cambridge with lots of input from Tom Minka Networks: Processes and Causality, September 2012

Outline • • • Graphical models of mixtures Gated graphs d-separation in gated graphs Inference in gated graphs Modelling interventions with gated graphs Causal inference with gated graphs

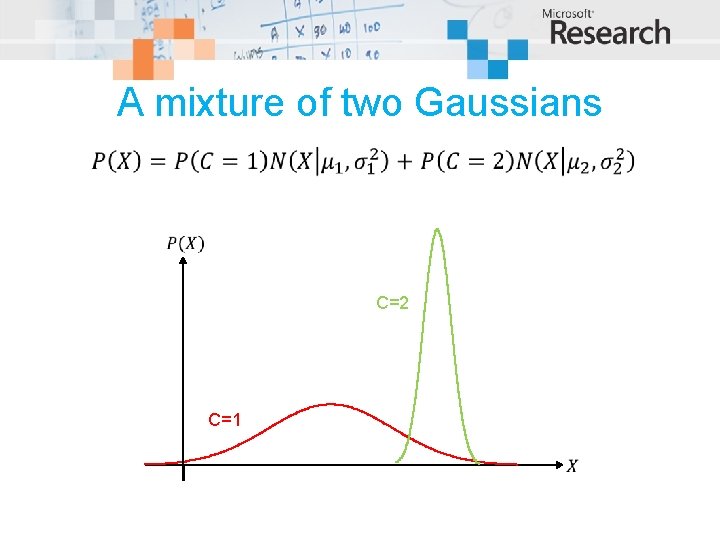
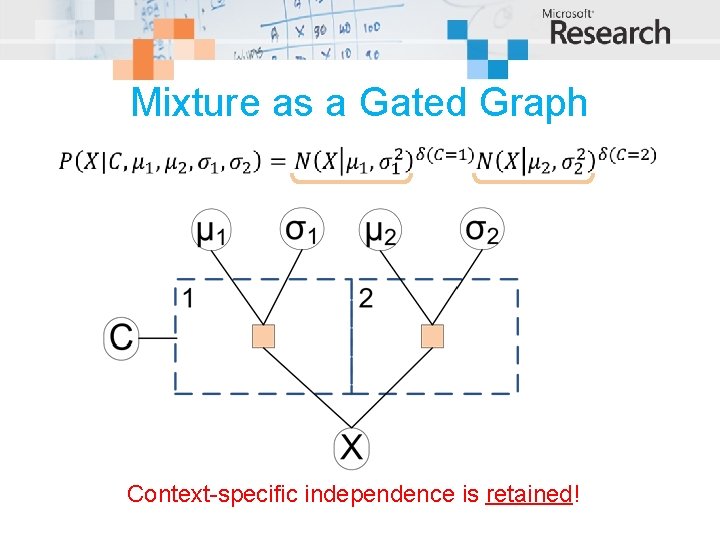
A mixture of two Gaussians C=2 C=1

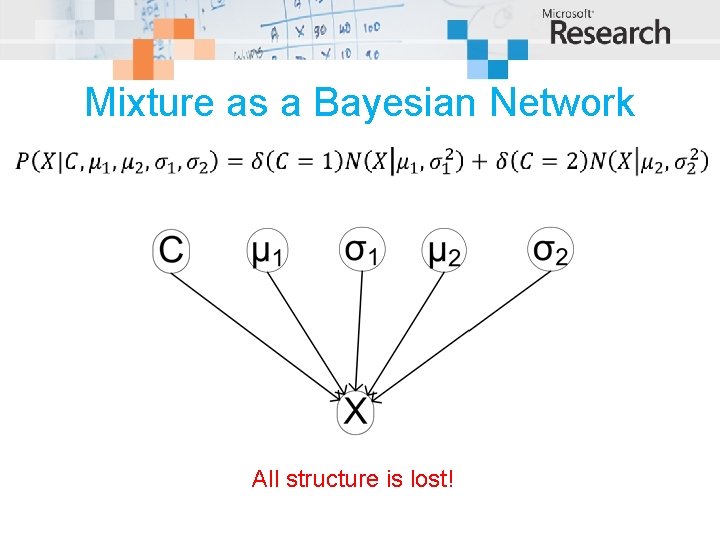
Mixture as a Bayesian Network All structure is lost!

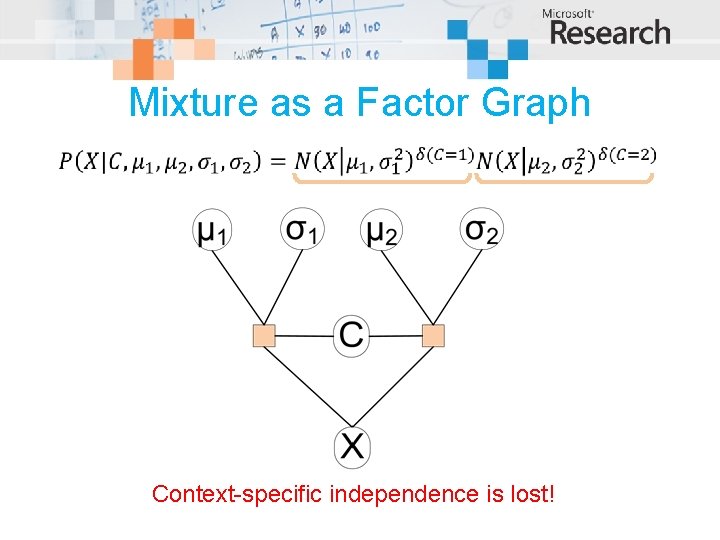
Mixture as a Factor Graph Context-specific independence is lost!

Mixture as a Gated Graph Context-specific independence is retained!

GATED GRAPHS

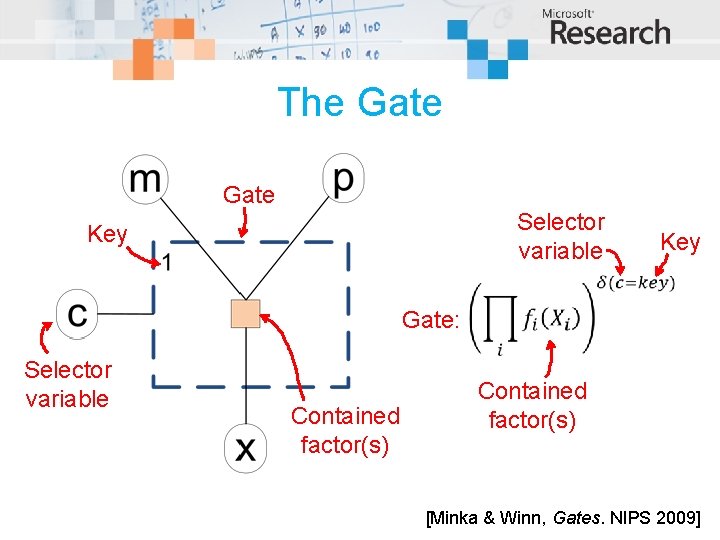
The Gate Selector variable Key Gate: Selector variable Contained factor(s) [Minka & Winn, Gates. NIPS 2009]

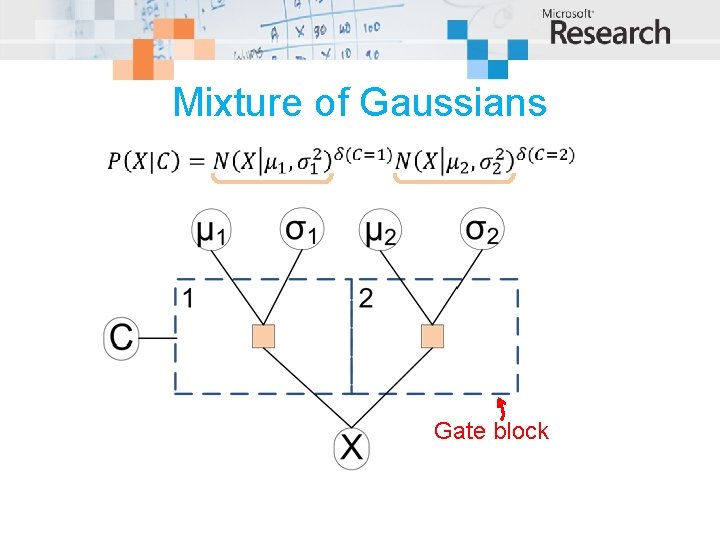
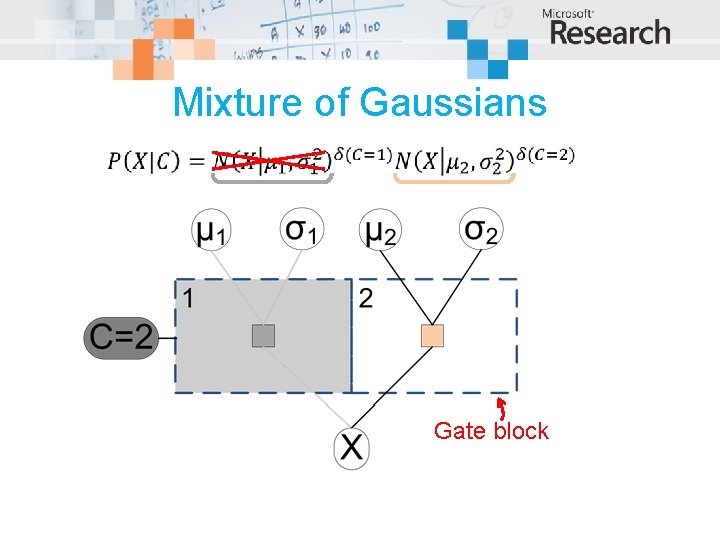
Mixture of Gaussians Gate block

Mixture of Gaussians Gate block

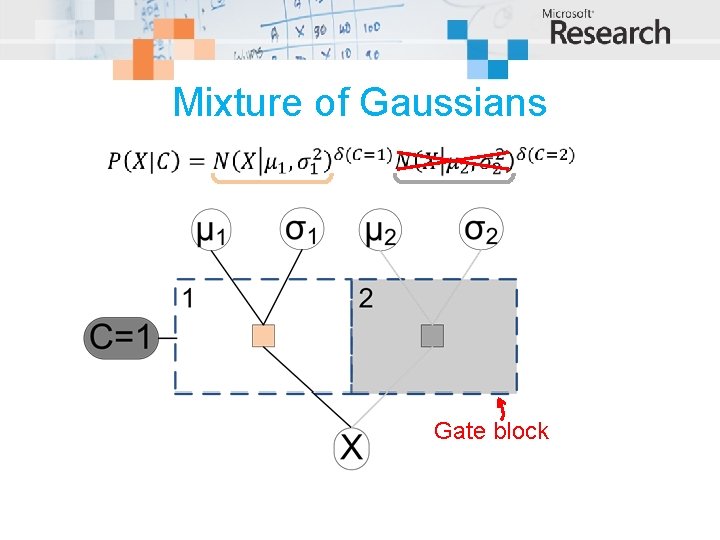
Mixture of Gaussians Gate block

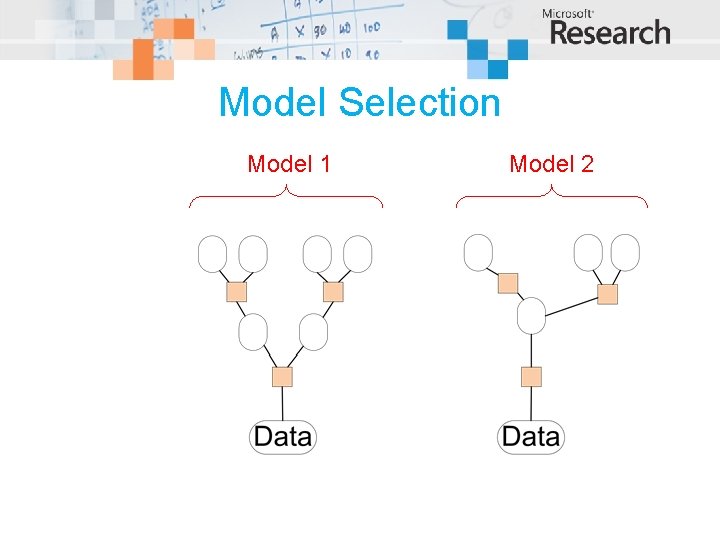
Model Selection Model 1 Model 2

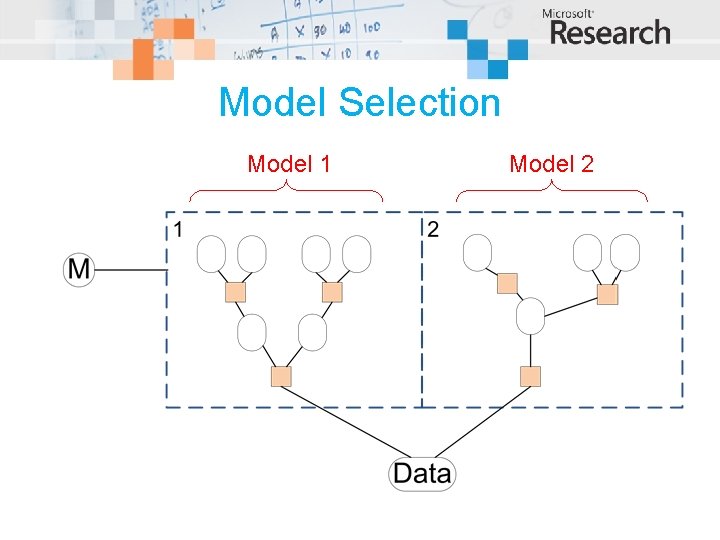
Model Selection Model 1 Model 2

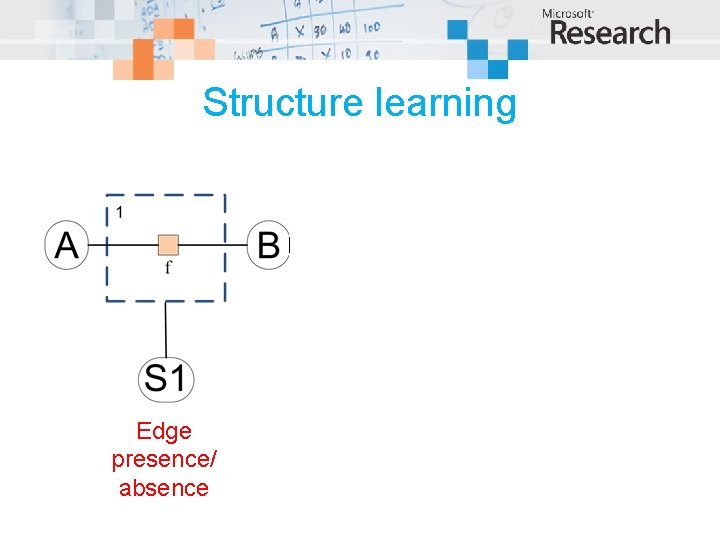
Structure learning Edge presence/ absence Edge type Variable presence/ absence

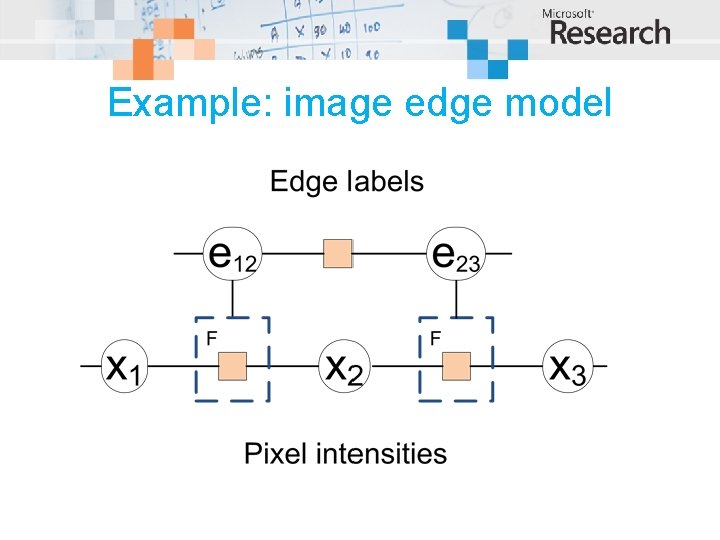
Example: image edge model

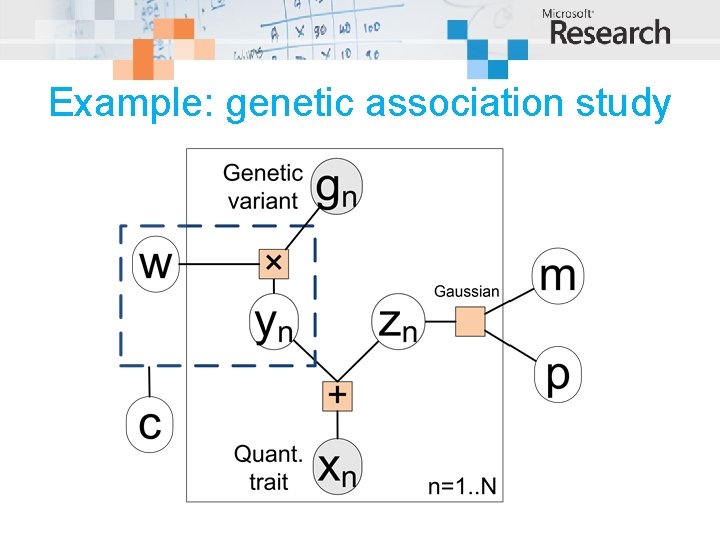
Example: genetic association study

D-SEPARATION IN GATED GRAPHS

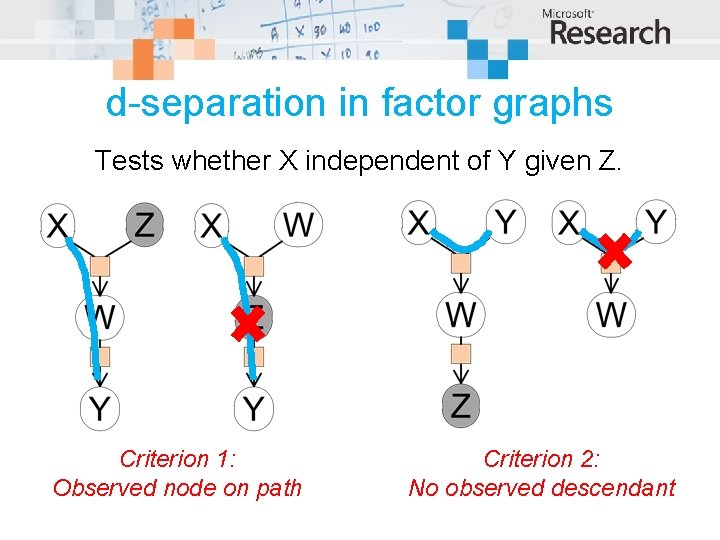
d-separation in factor graphs Tests whether X independent of Y given Z. Criterion 1: Observed node on path Criterion 2: No observed descendant

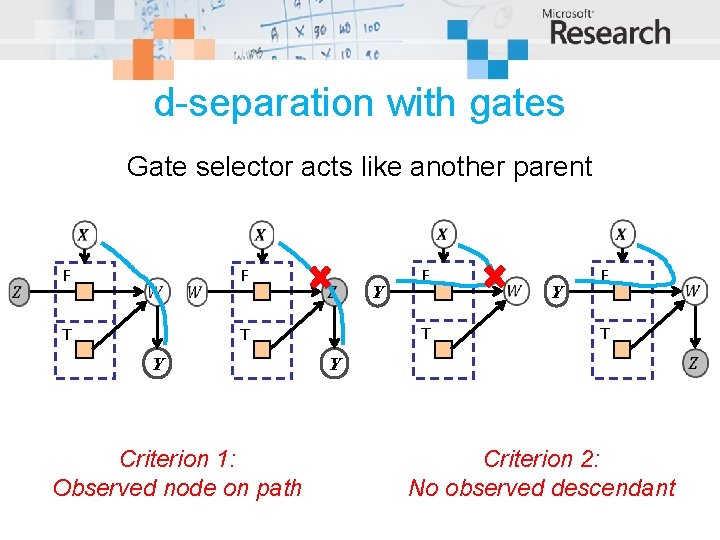
d-separation with gates Gate selector acts like another parent F T F T T Y Criterion 1: Observed node on path Y F T Y Criterion 2: No observed descendant

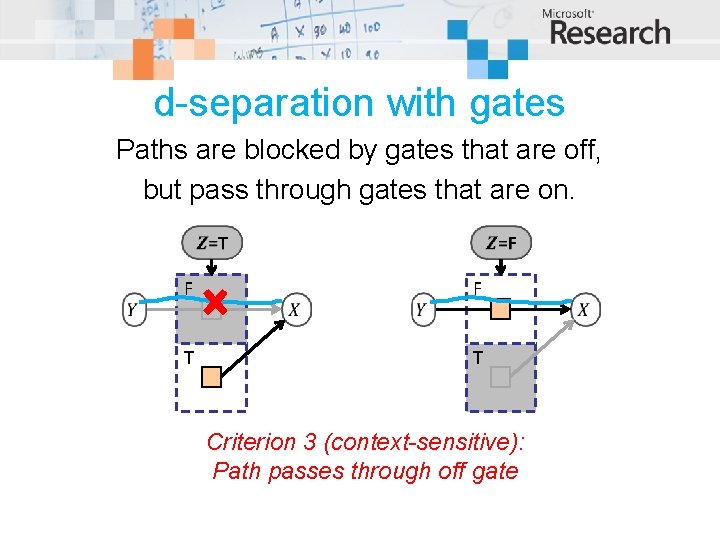
d-separation with gates Paths are blocked by gates that are off, but pass through gates that are on. F F T T Criterion 3 (context-sensitive): Path passes through off gate

d-separation summary Criterion 1: Observed node on path Criterion 2: No observed descendant Criterion 3: Path passes through off gate Allows new independencies to be detected, New! (even if they apply only in particular contexts)

INFERENCE IN GATED GRAPHS

Inference in Gated Graphs Extended forms of standard algorithms: • belief propagation • expectation propagation • variational message passing • Gibbs sampling Algorithms become more accurate + more efficient by exploiting conditional independencies. Free software at http: //research. microsoft. com/infernet [Minka & Winn, Gates. NIPS 2009]

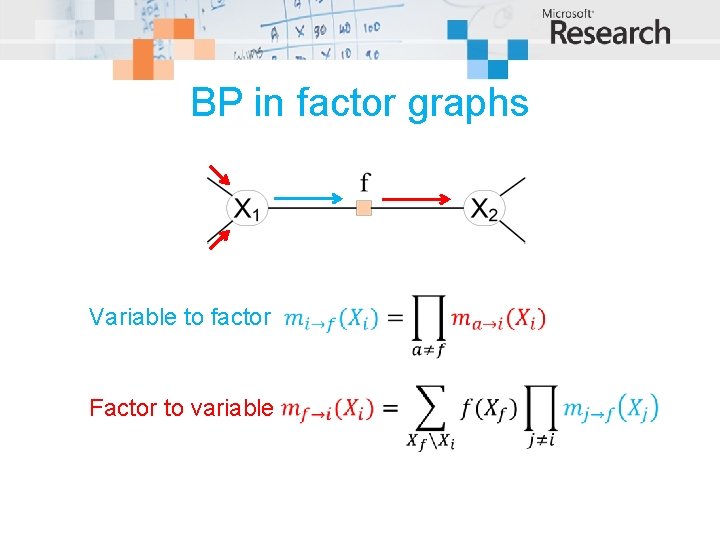
BP in factor graphs Variable to factor Factor to variable

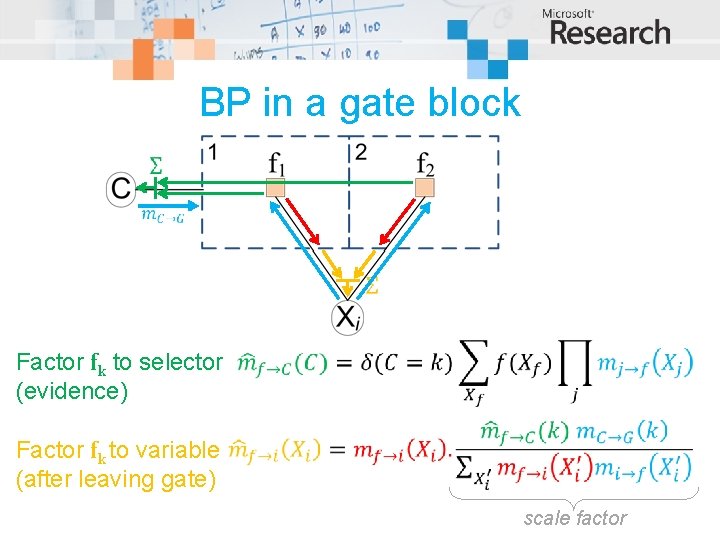
BP in a gate block Factor fk to selector (evidence) Factor fk to variable (after leaving gate) scale factor

MODELLING INTERVENTIONS WITH GATED GRAPHS (yes – I’m finally getting round to talking about causality)

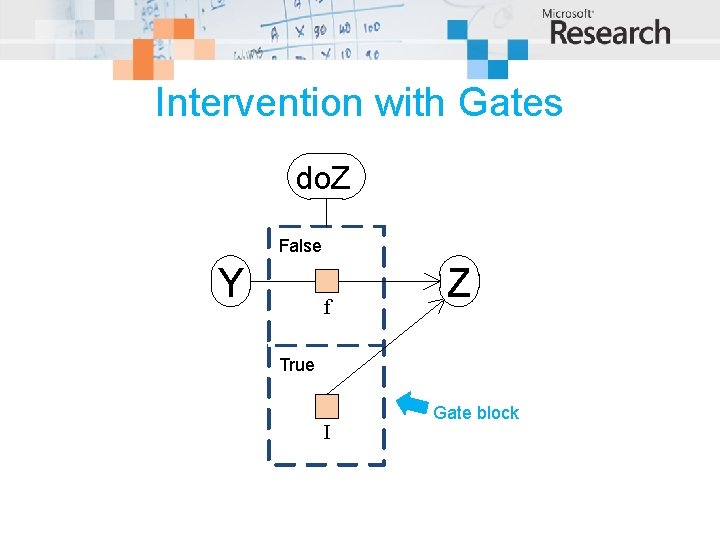
Intervention with Gates do. Z False Y f Z True I Gate block

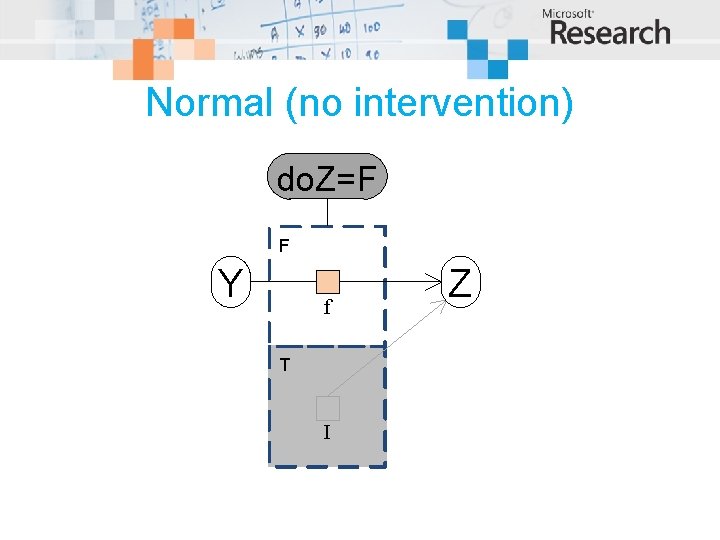
Normal (no intervention) do. Z=F F Y f T I Z

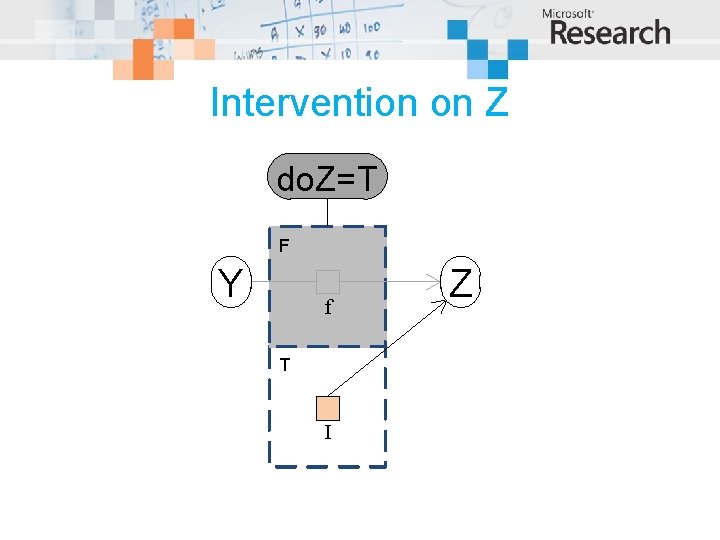
Intervention on Z do. Z=T F Y f T I Z

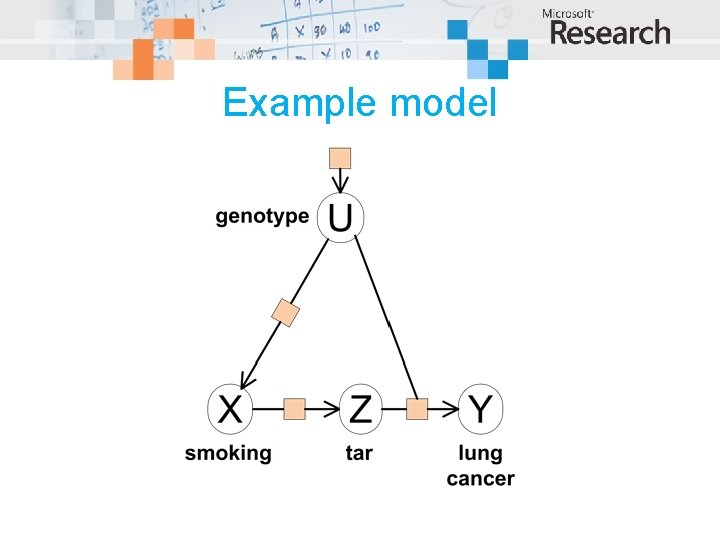
Example model

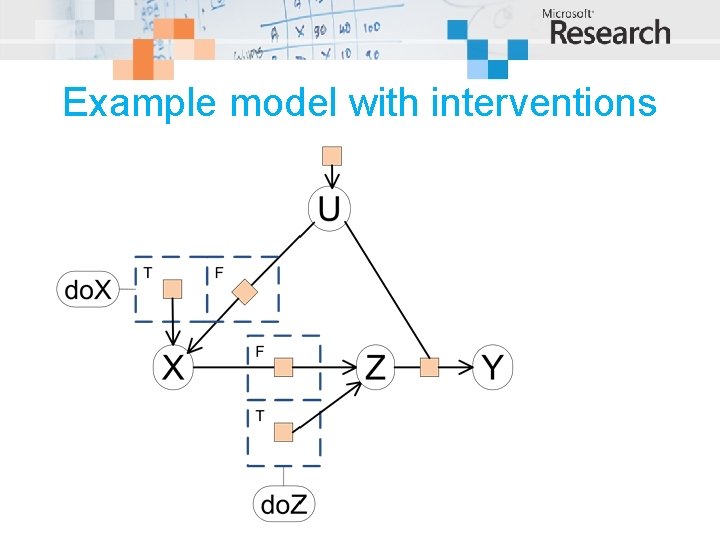
Example model with interventions
![do calculus Pearl Causal diagrams for empirical research Biometrika 1995 do calculus • [Pearl, Causal diagrams for empirical research, Biometrika 1995]](https://slidetodoc.com/presentation_image/5ead5f2b2a3df7537ef9c00ae8026eb3/image-32.jpg)
do calculus • [Pearl, Causal diagrams for empirical research, Biometrika 1995]

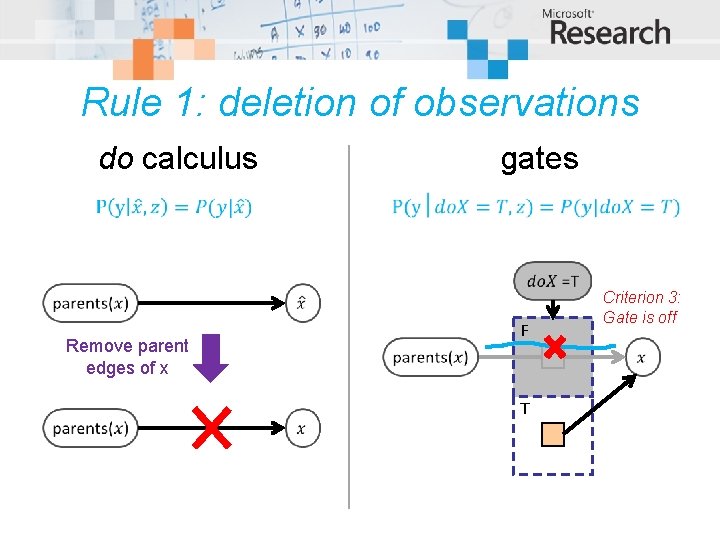
Rule 1: deletion of observations do calculus gates F Remove parent edges of x Criterion 3: Gate is off T

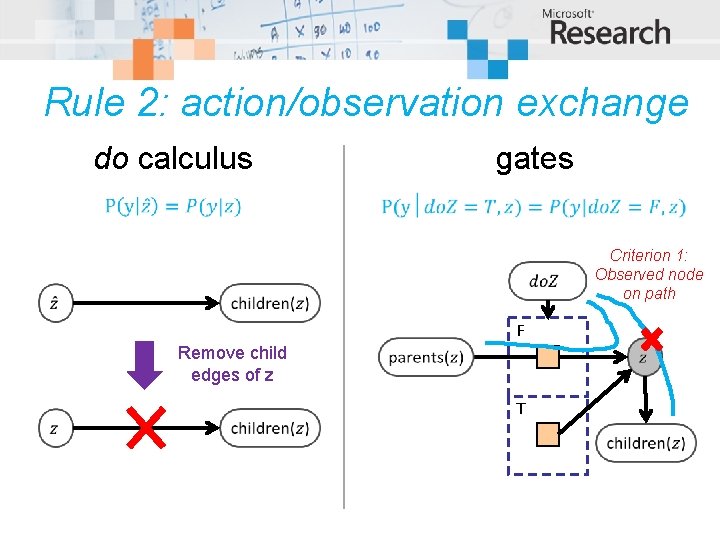
Rule 2: action/observation exchange do calculus gates Criterion 1: Observed node on path F Remove child edges of z T

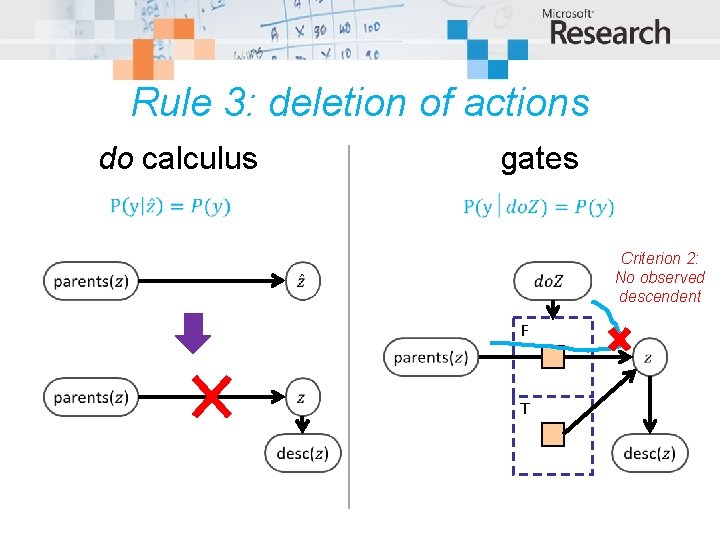
Rule 3: deletion of actions do calculus gates Criterion 2: No observed descendent F T

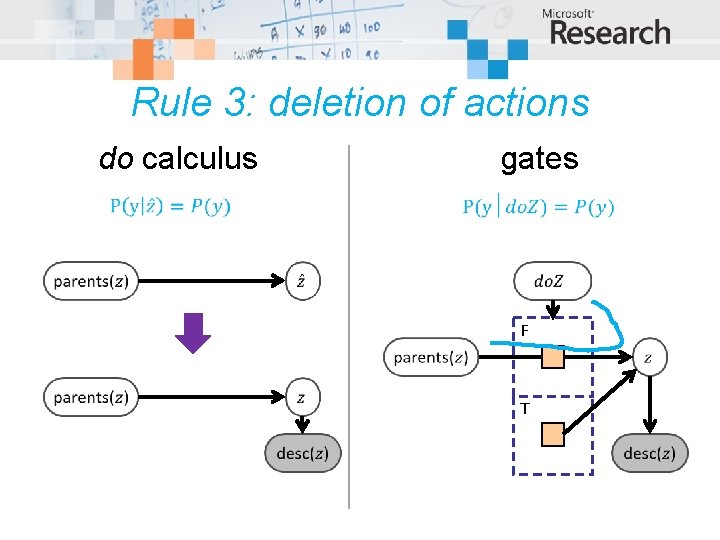
Rule 3: deletion of actions do calculus gates F T

do calculus equivalence The three rules of do calculus are a special case of the three d-separation criteria applied to the gated graph of an intervention.

CAUSAL INFERENCE WITH GATED GRAPHS

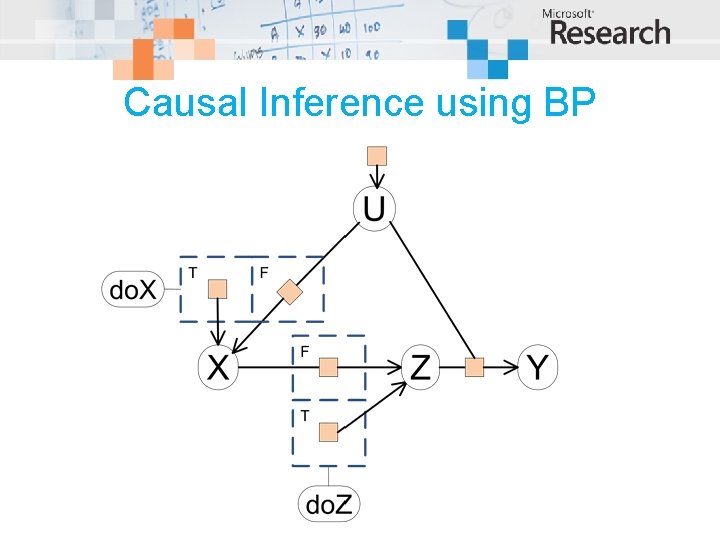
Causal Inference using BP

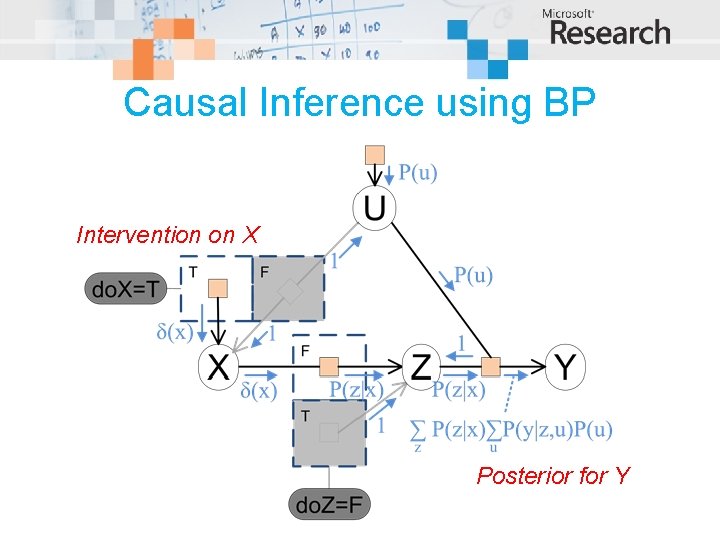
Causal Inference using BP Intervention on X Posterior for Y

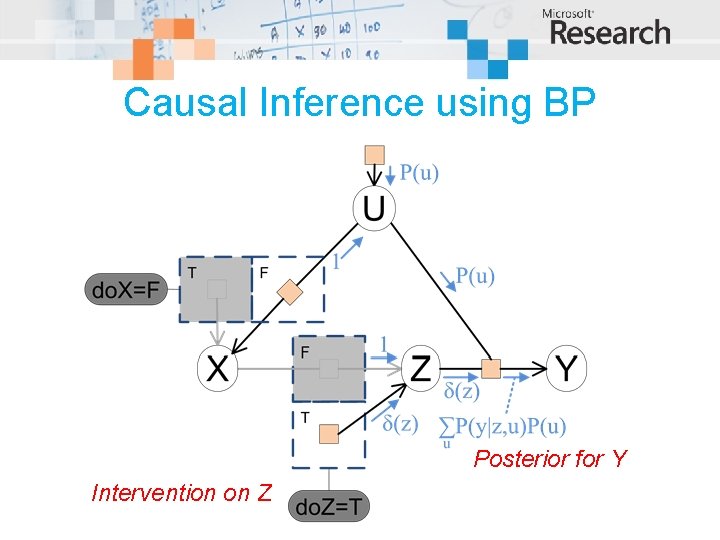
Causal Inference using BP Posterior for Y Intervention on Z

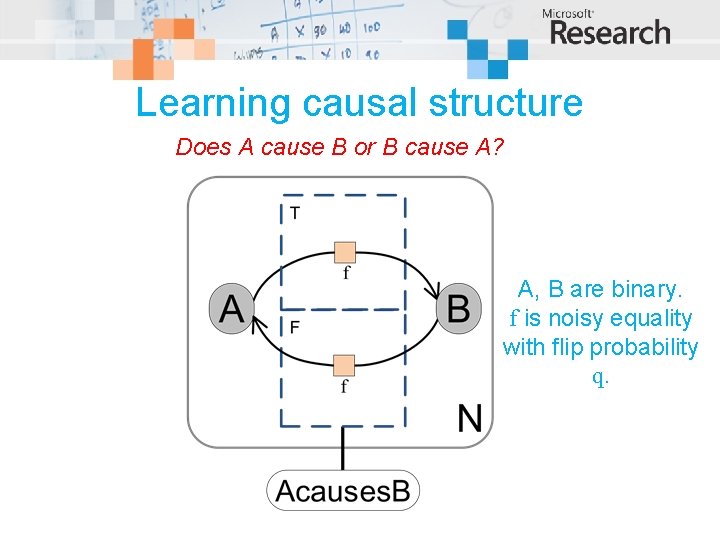
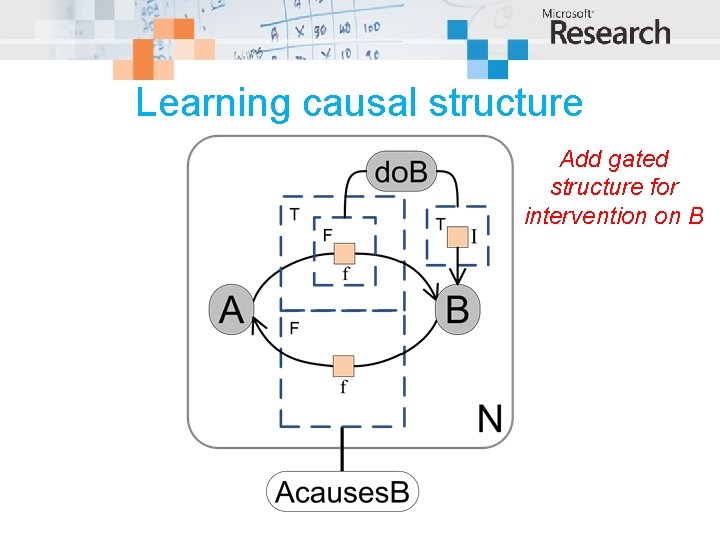
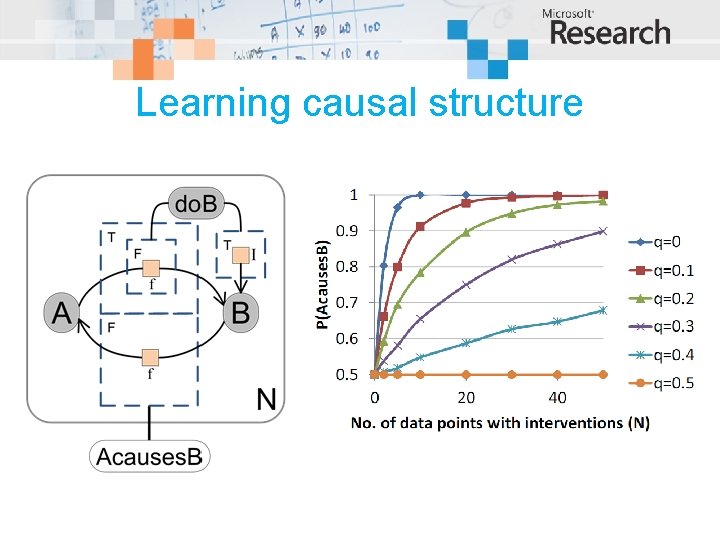
Learning causal structure Does A cause B or B cause A? A, B are binary. f is noisy equality with flip probability q.

Learning causal structure Add gated structure for intervention on B

Learning causal structure

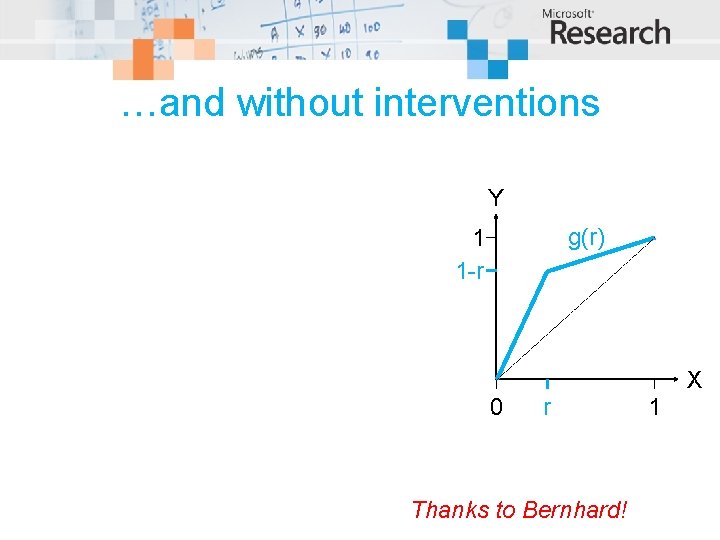
…and without interventions Y g(r) 1 1 -r X 0 r Thanks to Bernhard! 1

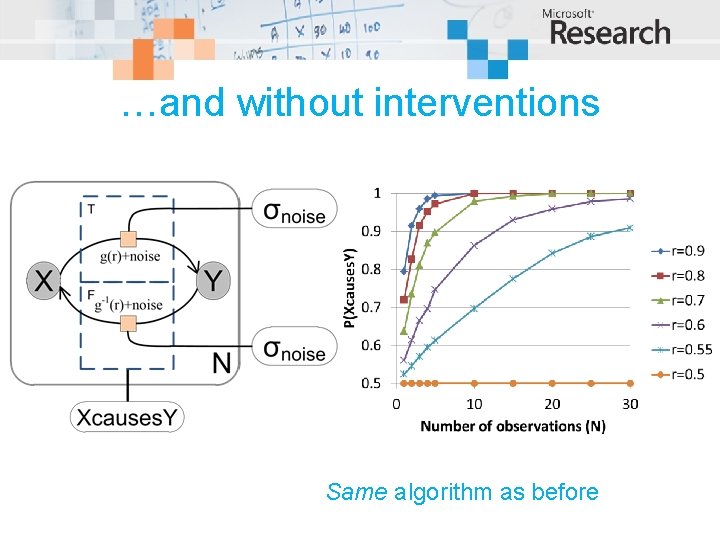
…and without interventions Same algorithm as before

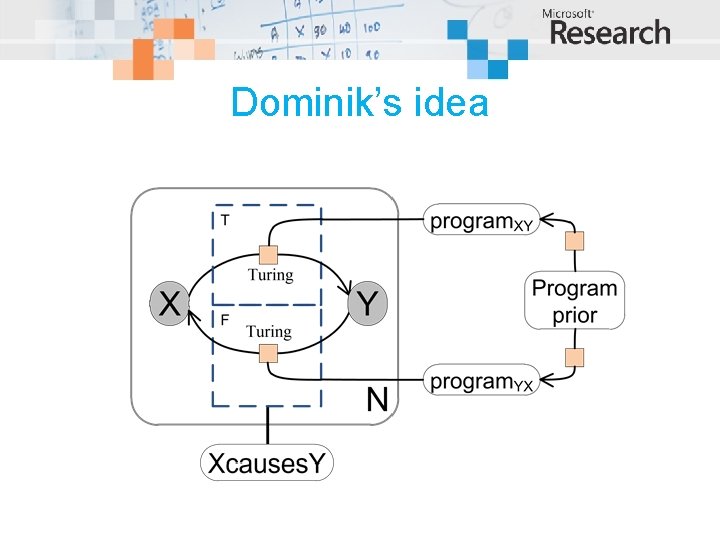
Dominik’s idea

Conclusions Causal reasoning is a special case of probabilistic inference: • The rules of do-calculus arise from testing d-separation in the gated graph. • Causal inference can be performed using probabilistic inference in the gated graph. • Causal structure can be discovered by using gates in two ways: – to model interventions and/or – to compare alternative structures.

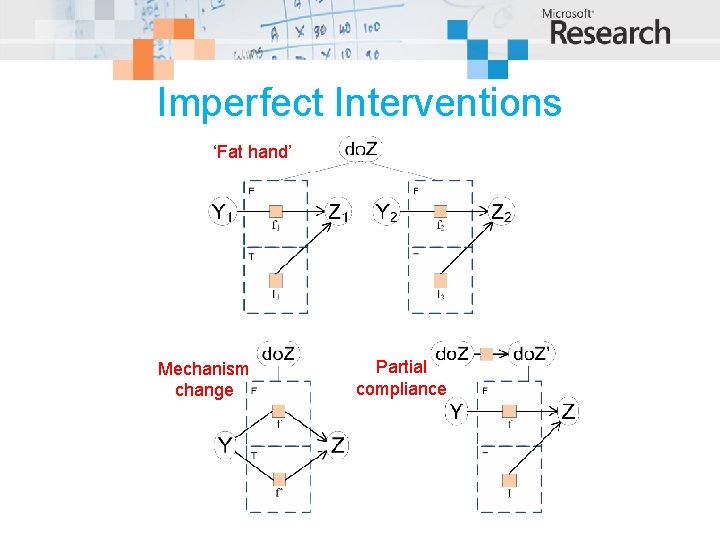
Future directions • Imperfect interventions – Partial compliance – Mechanism change • Counterfactuals – Variables that differ in the real and counterfactual worlds lie in different gates – Variables common to both worlds lie outside the gates

THANK YOU!

Imperfect Interventions ‘Fat hand’ Mechanism change Partial compliance
 Voltage gated vs ligand gated
Voltage gated vs ligand gated Descriptive and causal inference
Descriptive and causal inference Causal inference ai
Causal inference ai Causal inference techniques
Causal inference techniques Causal inference vs correlation
Causal inference vs correlation Causal inference
Causal inference Good and bad state graphs
Good and bad state graphs Graphs that enlighten and graphs that deceive
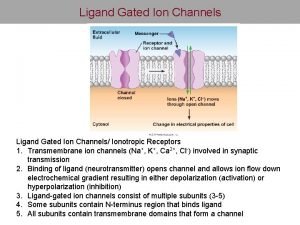
Graphs that enlighten and graphs that deceive Transmembrane ligand gated ion channel
Transmembrane ligand gated ion channel Speed and velocity
Speed and velocity End behavior of polynomials
End behavior of polynomials Andrew ng rnn
Andrew ng rnn Flipflops
Flipflops Gated d-latch
Gated d-latch Anatomy of the synapse
Anatomy of the synapse Gated wye friction loss
Gated wye friction loss Gated kick
Gated kick Inverse gated decoupling
Inverse gated decoupling Voltage gated sodium channel
Voltage gated sodium channel In primitive flow table for gated latch each state has
In primitive flow table for gated latch each state has Axon patch clamp amplifier
Axon patch clamp amplifier Depolarization sodium ions
Depolarization sodium ions Race condition occurs in gated sr latch when
Race condition occurs in gated sr latch when Sr nand latch
Sr nand latch Teardowns definition ap human geography
Teardowns definition ap human geography Because of winn dixie plot diagram
Because of winn dixie plot diagram Winn dixie interview questions and process
Winn dixie interview questions and process Winn equation
Winn equation Because of winn dixie
Because of winn dixie What is the genre of because of winn dixie
What is the genre of because of winn dixie Because of winn-dixie pictures
Because of winn-dixie pictures Miranda winn
Miranda winn India opal
India opal Jeremy winn
Jeremy winn Diane winn
Diane winn Colin winn
Colin winn Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Microsoft official academic course microsoft excel 2016
Microsoft official academic course microsoft excel 2016 Microsoft edge startwarren theverge
Microsoft edge startwarren theverge Microsoft excel merupakan program aplikasi dari
Microsoft excel merupakan program aplikasi dari Microsoft official academic course microsoft word 2016
Microsoft official academic course microsoft word 2016 Exploratory, descriptive and causal research
Exploratory, descriptive and causal research Correlational research
Correlational research Comperative of far
Comperative of far 2 key deliverables for causal analysis process
2 key deliverables for causal analysis process Causal analysis and resolution examples
Causal analysis and resolution examples Difference between conclusive and exploratory research
Difference between conclusive and exploratory research Cause and effect causal chain examples
Cause and effect causal chain examples Causal organism of neck and bulb rot in garlic is _____
Causal organism of neck and bulb rot in garlic is _____ The major emphasis in exploratory research is on
The major emphasis in exploratory research is on Networks and graphs: circuits, paths, and graph structures
Networks and graphs: circuits, paths, and graph structures Describing visual data
Describing visual data