Correlational and Causal Comparative Research Definition and Purpose

Correlational and Causal Comparative Research

Definition and Purpose Correlational research involves the collection of data to determine the extent to which two (or more) variables are related. If a relationship exists, we say that the two variables covary in some non-random way. The strength of the relationship is expressed as a correlation coefficient, r.

Correlational Research Concerned with examining the strength of associations (or relations) among two or more variables. Strength is expressed as a correlation coefficient between -1. 0 and +1. 0. The relationship can be positive or negative. Correlations with absolute values close to 1. 0 imply strong relationships; close to 0. 0 imply weak (or no) relationships.

Purpose of Correlation Research Descriptive: Show (or describe) the associations among variables. Hypothesis testing: Test whether variables expected to be related are, in fact, related. Theory driven. Correlations often occur spuriously. Should not examine correlations, first, and then construct a theory to explain them.

Correlational Research Design Collect data on two or more variables for each participant in the research study. Minimally accepted sample size is 30. If the measures have low reliability, larger sample sizes are needed. If participants are to be subdivided (say, into males and females) larges sample sizes are needed.

More on Sample Sizes Depends on the reliability of the measures. With reasonable reliability a minimum of 30 cases with bivariate measures is usually acceptable. The statistical test is a t test of the null hypothesis: H 0: xy = 0. 0

Analysis Correlation coefficients (rxy) describe both the size and direction of the relationship between two variables, x and y. Positive correlations close to +1. 0 indicate that two variables are strongly positively related (scores on one variable can be used to predict scores on the other). Negative correlations close to -1. 0 indicate that the two variables are strongly negatively correlated. Again scores on one can be used to predict scores on the other.

Analysis Assuming all or most of the coordinates (points) fall within the ellipse (of a scatter graph), the figure below represents a weak (near zero) correlation.

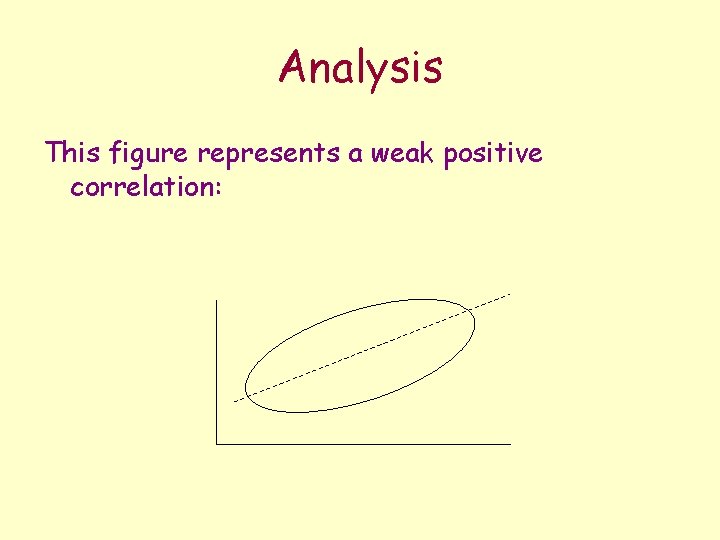
Analysis This figure represents a weak positive correlation:

Analysis Here we have a strong positive correlation:

Analysis This would be a representation of a weak negative correlation.

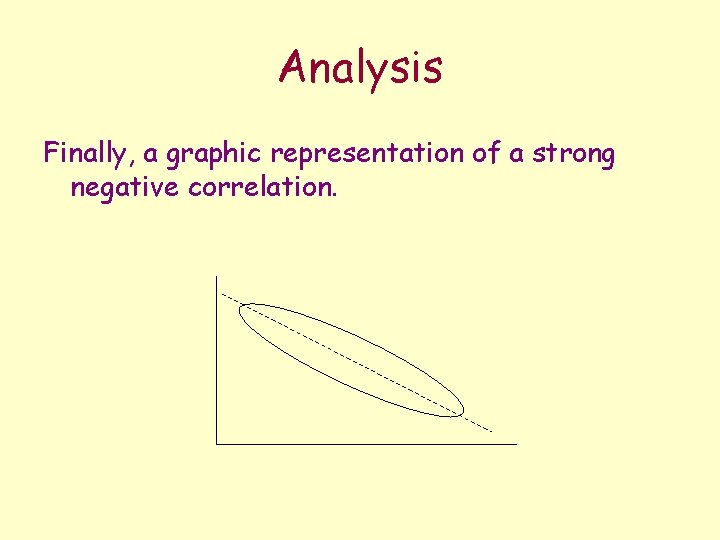
Analysis Finally, a graphic representation of a strong negative correlation.

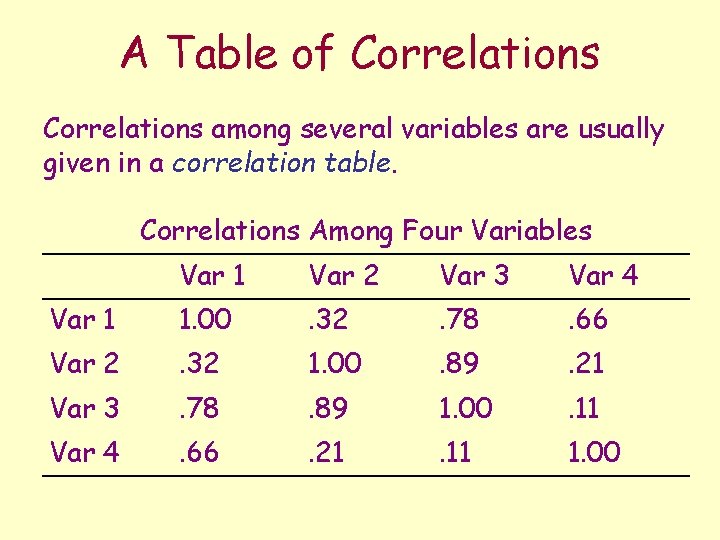
A Table of Correlations among several variables are usually given in a correlation table. Correlations Among Four Variables Var 1 Var 2 Var 3 Var 4 Var 1 1. 00 . 32 . 78 . 66 Var 2 . 32 1. 00 . 89 . 21 Var 3 . 78 . 89 1. 00 . 11 Var 4 . 66 . 21 . 11 1. 00

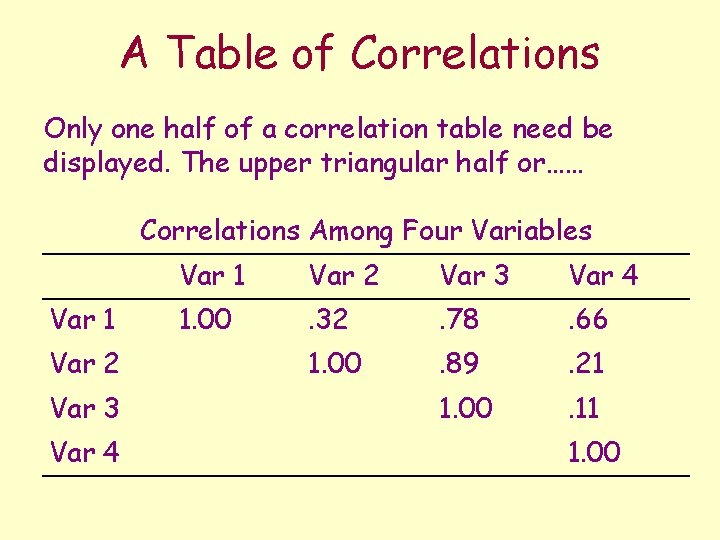
A Table of Correlations Only one half of a correlation table need be displayed. The upper triangular half or…… Correlations Among Four Variables Var 1 Var 2 Var 3 Var 4 1. 00 . 32 . 78 . 66 1. 00 . 89 . 21 1. 00 . 11 1. 00

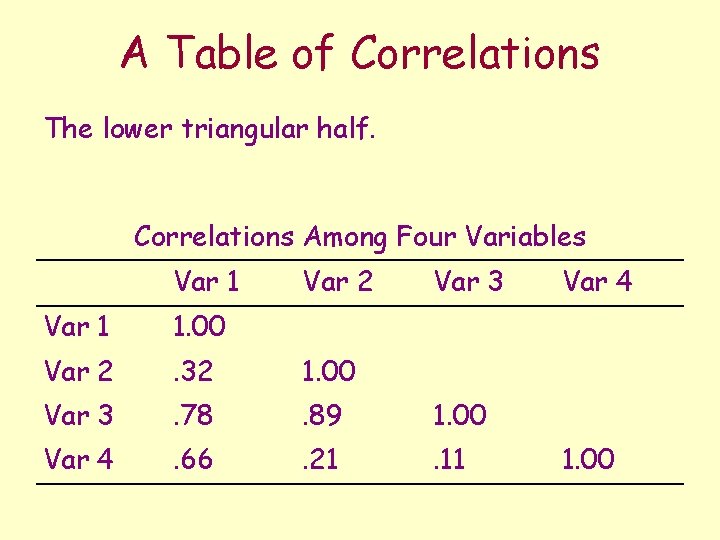
A Table of Correlations The lower triangular half. Correlations Among Four Variables Var 1 Var 2 Var 3 Var 1 1. 00 Var 2 . 32 1. 00 Var 3 . 78 . 89 1. 00 Var 4 . 66 . 21 . 11 Var 4 1. 00

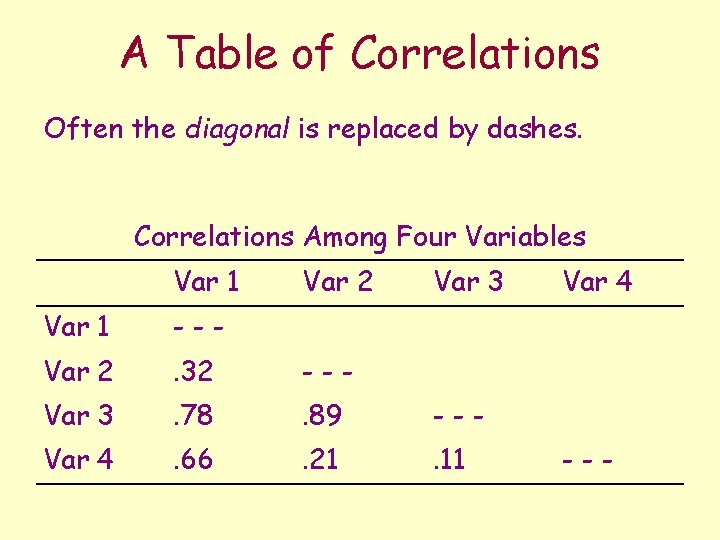
A Table of Correlations Often the diagonal is replaced by dashes. Correlations Among Four Variables Var 1 Var 2 Var 3 Var 1 --- Var 2 . 32 --- Var 3 . 78 . 89 --- Var 4 . 66 . 21 . 11 Var 4 ---

How large should a correlation be? Correlations where Abs(rxy ) >. 50 are typically useful for prediction purposes The square of the correlation coefficient (rxy 2) gives the percent of variation x and y have in common. The size of the correlation required in order to be useful depends on the purpose.

Statistical significance and Practical significance Correlation coefficients should not be interpreted unless it is first shown that the coefficient is statistically significant (i. e. , until we can state that there is sufficient statistical evidence that the correlation is NOT zero). With large enough samples, even small correlations can be statistically significant. Statistically significant correlations may not be practically significant. A low correlation is still a low correlation.

Linear correlations vs Curvilinear correlations The chart below indicates a correlation between two variables that has a nearzero linear correlation but a strong curvilinear correlation.

Causal-Comparative Research Also called ex post facto research. An attempt is made to find the cause or explanation for existing differences between (or among) groups. Two or more existing groups are compared retrospectively. Note that in correlational research we had one group and two or more variables. Here we have two or more groups and one variable.

Causal-Comparative research vs Experimental research In experimental research (or quasi-experimental research) the researcher controls the administration of the independent variable. In causal-comparative research the groups being formed have already been differentiated according to the independent variable (e. g. , either they have been exposed to pre-school or not).

Causal Comparative Research Groups… are classified according to common preexisting characteristic, and compared on some other measure There is NO intervention, manipulation, or random assignment

Major difficulty: Establishing the cause. Three conditions for establishing causeeffect relationships: 1. The presumed cause must precede the effect. 2. The relationship between the cause and effect must be statistically significant. 3. Other probable causes must be eliminated (most difficult condition to meet).

Spurious Causation Here are two examples of spurious causation. In the top example, the correlation between A and C requires the mediator, B. In the bottom example the correlation between B and C exists because both variables are caused by A. A B B C C A

Reaching Conclusions At best, causal-comparative research produces evidence that supports a theoretical conjecture. The strength of evidence relies heavily on two things: 1. The extent to which rival causes can be ruled out. 2. The extent to which the results can be predicted (according to theory) beforehand.

Conducting a Causal-Comparative Study Identify two or more populations (or groups) that differ on some independent variable (IV) of interest (e. g. , novice teachers and veteran teachers). Formulate some theory about how the groups should perform differently on some dependent variable (DV) of interest (e. g. , classroom management). Select representative samples from the populations and compare them on the dependent variable.

Two Variations of Causal Comparative Studies There are two ways to approach causalcomparative research: • Prospective: start with a presumed cause an investigate effects (not very common in social science/education research). • Retrospective: start with a presumed effect and investigate possible causes (these are more prevalent in social science/education research).

Examples of the Two Variations Investigate the relationship between gender and career aspirations or career choice. • Retrospective: Groups identified on the basis of career choice and then compared by gender. • Prospective: Groups formed on the basis of gender, and compared on strength of career aspirations.

Examples of the Two Variations Investigate the relationship of time watching TV (the IV) on academic achievement (the DV) • Prospective: Form groups on the basis of how much TV they watch and compare them on academic achievement (say, GPA). • Retrospective: Form groups on the basis of academic achievement (say, class rank) and compare this to hours of TV watched.

Examples of the Two Variations Investigate the effect of time parents spend reading to children and children’s reading readiness when entering 1 st grade. • Retrospective: Groups formed on the basis of a reading-readiness test score, and compare in terms of time parents spend reading to their children. • Prospective: Form groups of children in terms of time their parents spent reading to them and compare the children on reading readiness scores.

Examples of the Two Variations Investigate the effect of mentoring and tendency to drop out of high school. • Prospective: Groups formed on the basis of whether they enjoyed a mentoring relationship while in high school and compared in terms of whether they dropped out of high school • Retrospective: Groups formed on the basis of whether they dropped out of high school, and compared on whether they enjoyed a mentoring relationship prior to dropping out.

Example Causal-Comparative Study: What causes lung cancer? Finding: People with lung cancer smoke more than people without lung cancer. There are no other differences in lifestyle characteristics between the groups. Conclusion: Smoking is a possible cause of lung cancer. Caution: Is there a third factor that might explain lung cancer AND smoking?

Weaknesses and Controls Lack of randomization, inability to manipulate the independent variables, lack of controls of extraneous variables are all weaknesses in causal-comparative research. Three approaches that help ameliorate some of the problems are: 1. Matching, 2. Comparing homogeneous groups, and 3. Analysis of covariance (to be discussed later).

Strengthening Causal Comparative Designs Strong inference (theory plays a major role). Time sequence (presumed cause precedes presumed effect). Incorporate other, possible, causes in the design (measure common antecedents). Use designs that control for possibl extraneous causes: • matched group design • Extreme groups design • Statistical control (Analysis of Covariance)

Establishing Causal Relationships From John Stuart Mills • Establish a temporal sequence (the presumed cause must precede the presumed effect). • Establish a statistical relation ship between the presumed cause and effect (correlations among variables or differences among groups). • Rule-out possible rival causes (control for, or eliminate extraneous sources of influence). • This is often the most difficult condition. • Strong theory plays an important role here.

Wide Variety of Statistical Procedures t tests, ANOVA, ANCOVA when two or more groups are being compared. Regression analysis when there are multiple independent variables. MANOVA, and multivariate regression, when there are multiple dependent variables. Path analysis and structural equation modeling when theoretical causal paths are being investigated.

END