Fundamentos de Mecnica 4300151 Primeiro semestre de 2020






















- Slides: 40

Fundamentos de Mecânica 4300151 – Primeiro semestre de 2020 9 a Aula Nilberto Medina e Vito Vanin medina@if. usp. br, vanin@if. usp. br 02/04/2020

AVISOS Questionário C 4 sobre Conceitos de Matemática estará aberto até hoje. Leiam o texto e façam as questões e exercícios antes de realizar o teste. Monitoria sobre Mecânica Experimental com Imagens terça e quinta-feira das 12 às 13 e das 18 às 19 horas (ZOOM) Entrega do relatório até 02 de abril às 23: 59 horas via moodle (UPLOAD) 5 a feira a partir das 10 e 6ª-feira a partir das 21 horas Conceitos de Matemática, pelo programa Zoom Leitura cap. 2 HRK seções 2. 5 e 2. 6 cap. 3 HRK seções 3. 1 a 3. 5 Semana que vem: aula e monitoria 2ª, 3ª e 4ª; recesso na 5ª e 6ª 2

Revisão letras que representam variáveis mudas nessas equações, embora muitas letras tenham uso convencional Derivada de uma função f(x) Uma curva é formada por muitas retas Cinemática: posição velocidade Aceleração É a inclinação da pequena reta em torno do 3 Halliday, Resnick e Krane, seção 2 -5 e 2 -6

Movimento unidimensional Derivada de uma função f(x) Exemplo: gráficos da queda livre y(t), v(t) e a(t) Halliday, Resnick e Krane, seção 2 -5 e 2 -6

A equação da reta tangente; aceleração e concavidade

Traçando uma tangente a uma parábola Vamos usar as unidades de base do SI em todas as grandezas deste slide Abaixo, a função Vamos traçar a reta tangente em t = 2 s Em t = 2, portanto a reta tem inclinação = 10 m/s Agora usamos a fórmula e deduzimos ou 2

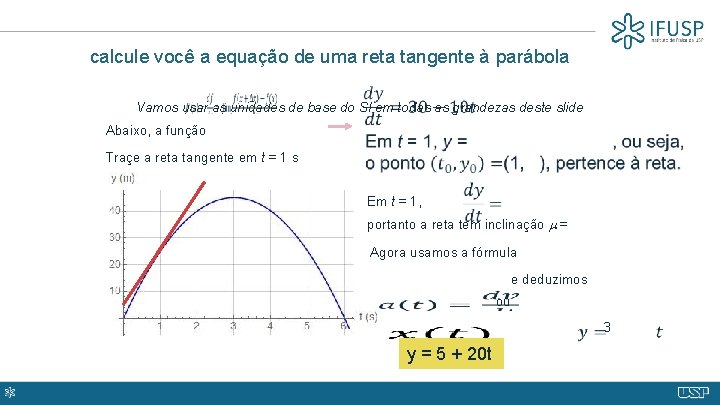
calcule você a equação de uma reta tangente à parábola Vamos usar as unidades de base do SI em todas as grandezas deste slide Abaixo, a função Traçe a reta tangente em t = 1 s Em t = 1, portanto a reta tem inclinação = Agora usamos a fórmula e deduzimos ou y = 5 + 20 t 3

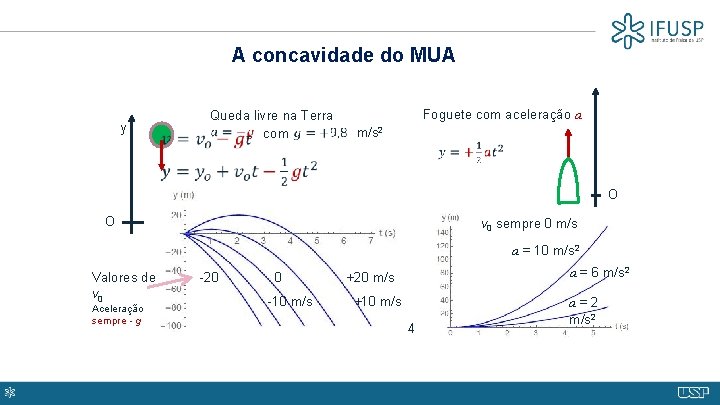
A concavidade do MUA y Queda livre na Terra com Foguete com aceleração a m/s 2 O O v 0 sempre 0 m/s a = 10 m/s 2 Valores de v 0 Aceleração sempre - g a = 6 m/s 2 -20 +20 m/s -10 m/s +10 m/s 4 a = 2 m/s 2 3

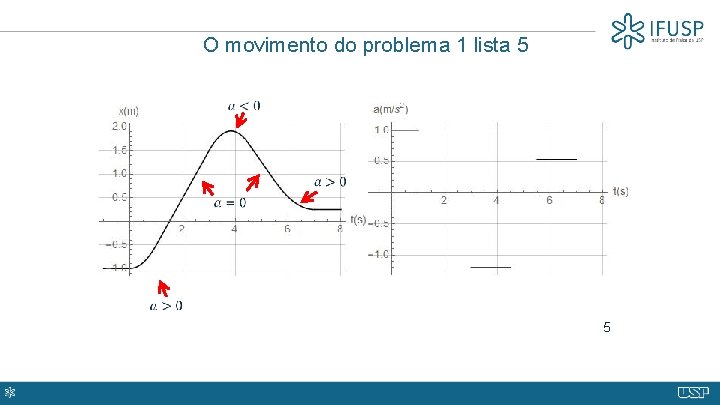
O movimento do problema 1 lista 5 5

O movimento harmônico simples O gráfico em azul representa o movimento de um oscilador harmônico (pode ser uma massa presa numa mola, ou um pêndulo com pequenas oscilações) de período 1 s. No intervalo 0 < t < 0, 5 s, a curva é côncava para baixo aceleração negativa. No intervalo 0, 5 < t < 1 s, a curva é côncava para cima aceleração positiva. 6

Lista 5

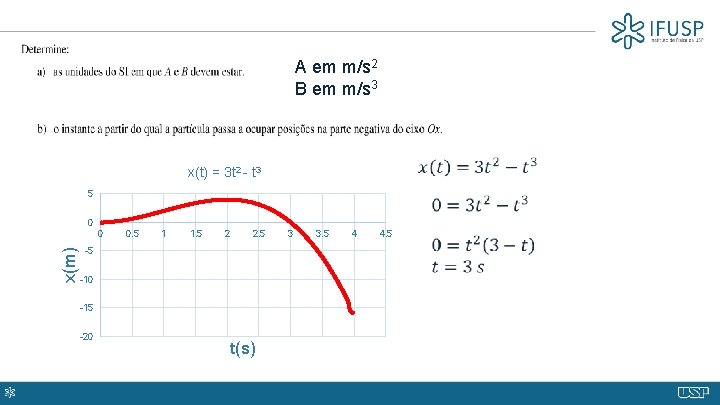
A em m/s 2 B em m/s 3 x(t) = 3 t 2 - t 3 5 0 x(m) 0 0. 5 1 1. 5 2 2. 5 3. 5 4 4. 5 -5 -10 -15 -20 3 t(s)

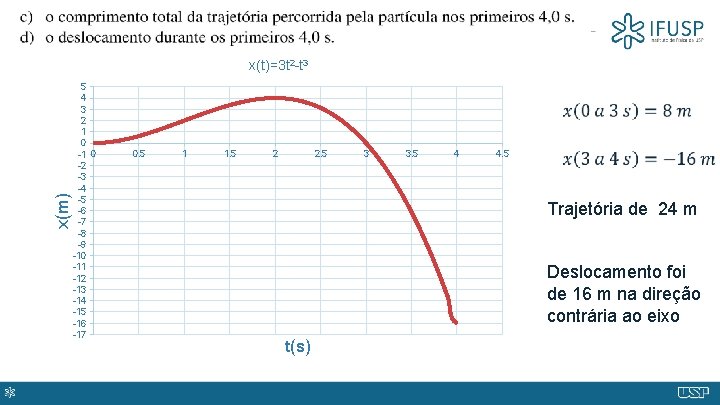
x(m) x(t)=3 t 2 -t 3 5 4 3 2 1 0 -2 -3 -4 -5 -6 -7 -8 -9 -10 -11 -12 -13 -14 -15 -16 -17 0. 5 1 1. 5 2 2. 5 3 3. 5 4 4. 5 Trajetória de 24 m Deslocamento foi de 16 m na direção contrária ao eixo t(s)


Segunda Lei de Newton Halliday, Resnick e Krane, seção 2 -5 e 2 -6

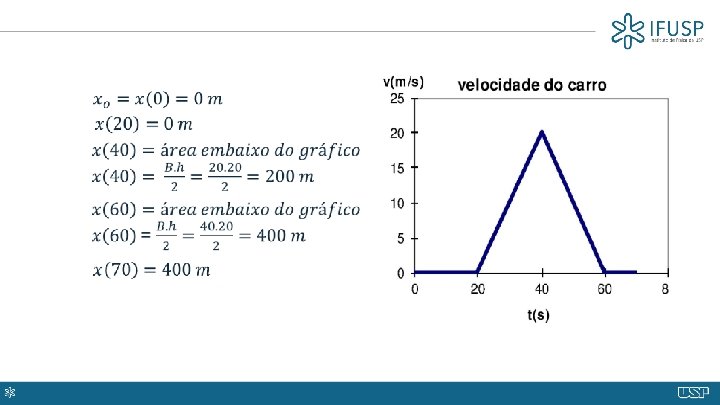
Determinação da posição de um objeto a partir do gráfico de v(t) Antiderivada

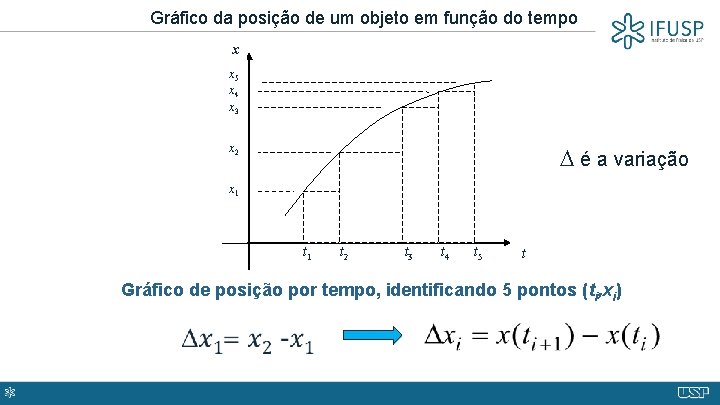
Gráfico da posição de um objeto em função do tempo x x 5 x 4 x 3 x 2 D é a variação x 1 O t 1 t 2 t 3 t 4 t 5 t Gráfico de posição por tempo, identificando 5 pontos (ti, xi)


Integral

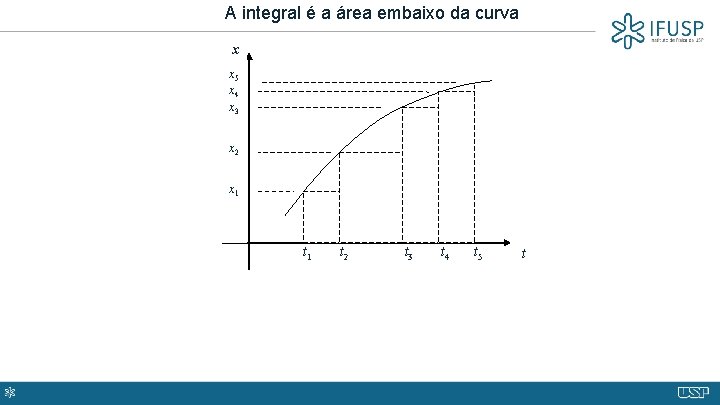
A integral é a área embaixo da curva x x 5 x 4 x 3 x 2 x 1 O t 1 t 2 t 3 t 4 t 5 t


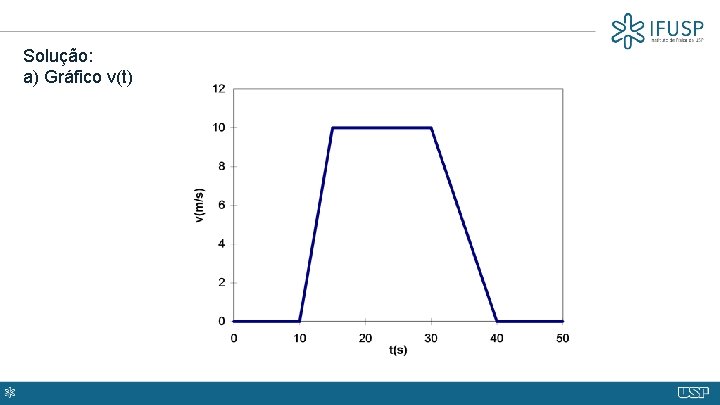
Exemplo 1. O motorista de um ônibus no trânsito urbano, parado em um farol, começa a acelerar em t = 10 s com aceleração constante e igual a 2, 0 m/s 2 até atingir 36 km/h, mantendo essa velocidade por 15 s, quando avista o farol seguinte fechado e começa a frear, com aceleração constante e de módulo 1, 0 m/s 2 , até parar completamente o veículo. a) Faça um gráfico da velocidade em função do tempo. b) Determine a distância que o veículo percorreu entre as duas paradas. c) Determine o instante em que o veículo se encontrava a 200 m do ponto de partida.

Solução: a) Gráfico v(t)

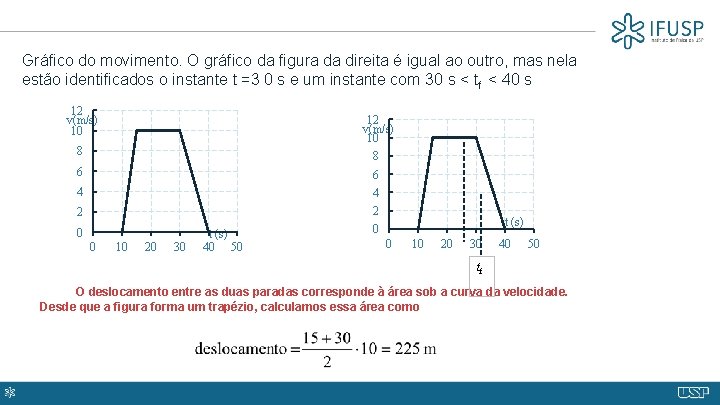
Gráfico do movimento. O gráfico da figura da direita é igual ao outro, mas nela estão identificados o instante t =3 0 s e um instante com 30 s < tf < 40 s 12 v(m/s) 10 8 8 6 6 4 4 2 2 0 0 10 20 30 t (s) 40 50 t (s) 0 0 10 20 30 40 50 tf O deslocamento entre as duas paradas corresponde à área sob a curva da velocidade. Desde que a figura forma um trapézio, calculamos essa área como

(c) O veículo de fato passou por um ponto a 200 m do ponto de partida, porque o percurso total foi maior que esse, conforme o cálculo do item (b) acima. Ao invés de determinar a equação horária para qualquer t, que será complexa uma vez que o movimento tem aceleração variável, determinamos um intervalo de tempo curto em que o veículo passa por esse ponto e escrevemos uma equação mais detalhada apenas para esse intervalo. O deslocamento até t = 30 s, calculado por uma forma análoga à usada no item (b), é . Juntando com o resultado do item (b), vemos que o veículo está a 200 m do ponto de partida em algum instante compreendido entre t = 30 s e t = 40 s.

Na gráfico à direita na figura 1, demarcamos com linhas tracejadas a região do gráfico cuja área corresponde ao deslocamento entre t = 30 s e um certo instante de tempo tf. O instante de tempo que buscamos corresponde a tf desde que o deslocamento seja de 25 m (obtido pela diferença entre o ponto determinado pela questão, 200 m, e o deslocamento até t = 30 s, 175 m). A equação obtida impondo-se essa condição é tendo sido calculada como a da área de um trapézio (que agora está deitado, a altura está na abscissa). Resolvendo essa equação do 2 o grau, obtemos tf = 32, 9 s 33 s, que é o instante em que o veículo alcançou um ponto a 200 m do ponto de partida.


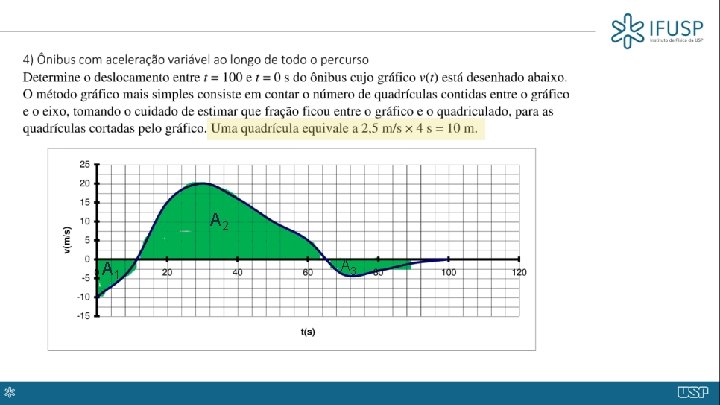
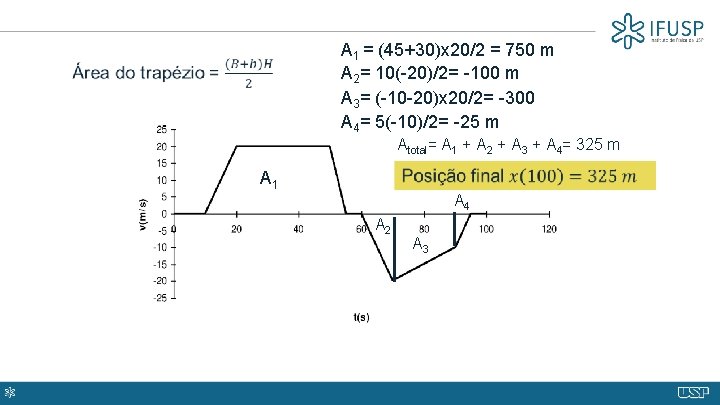
A 2 A 1 A 3

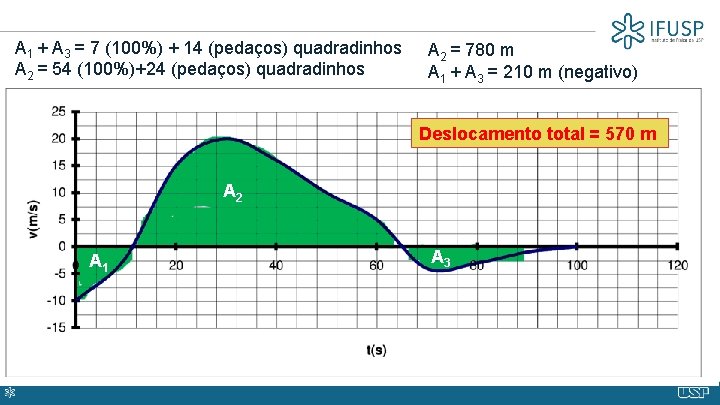
A 1 + A 3 = 7 (100%) + 14 (pedaços) quadradinhos A 2 = 54 (100%)+24 (pedaços) quadradinhos A 2 = 780 m A 1 + A 3 = 210 m (negativo) Deslocamento total = 570 m A 2 A 1 A 3



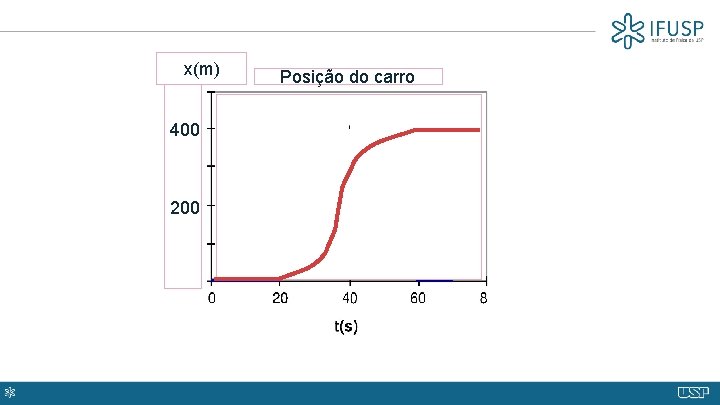
x(m) 400 200 Posição do carro

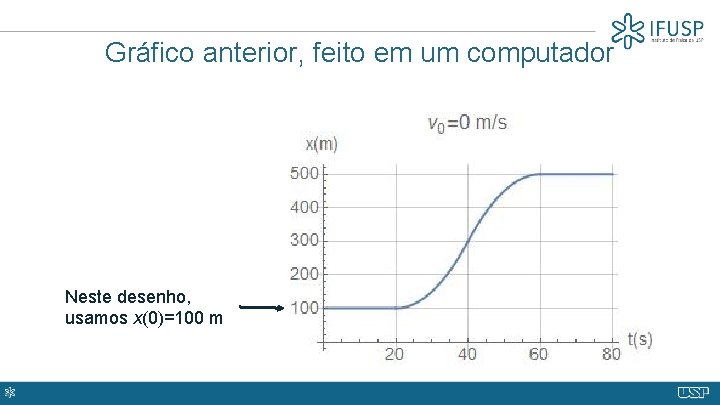
Gráfico anterior, feito em um computador Neste desenho, usamos x(0)=100 m


A 1 = (45+30)x 20/2 = 750 m A 2= 10(-20)/2= -100 m A 3= (-10 -20)x 20/2= -300 A 4= 5(-10)/2= -25 m Atotal= A 1 + A 2 + A 3 + A 4= 325 m A 1 A 4 A 2 A 3

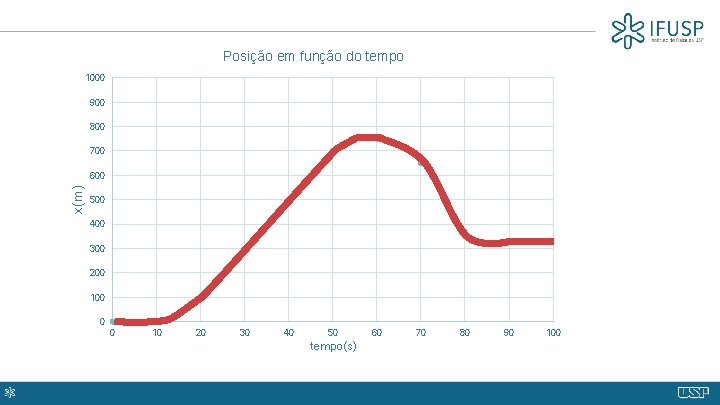
Posição em função do tempo 1000 900 800 700 x(m) 600 500 400 300 200 100 0 0 10 20 30 40 50 tempo(s) 60 70 80 90 100

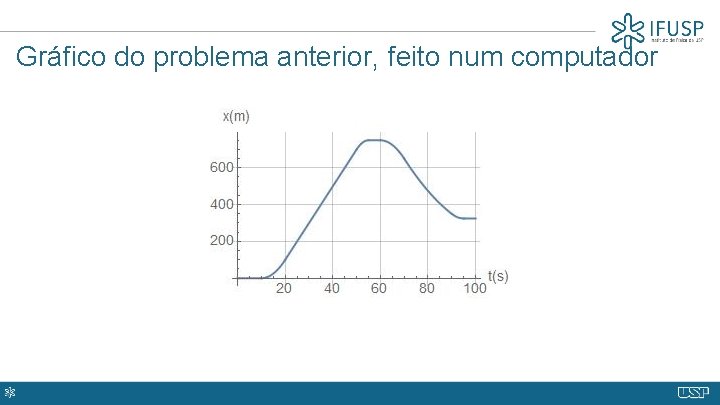
Gráfico do problema anterior, feito num computador


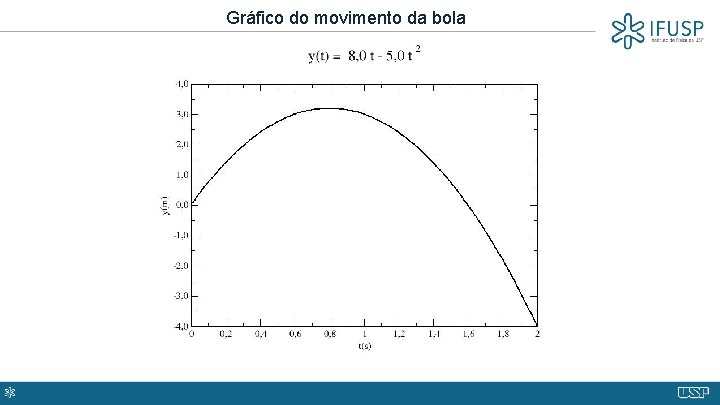
a) Velocidade da bola b) Altura máxima que a bola atinge após a janela para v = 0 m/s

Gráfico do movimento da bola
 Mecnica
Mecnica Mecnica
Mecnica Semestre avanzado universidad de cundinamarca
Semestre avanzado universidad de cundinamarca Rapport semestre 1
Rapport semestre 1 10 semestre
10 semestre Que quiero lograr en mi vida ejemplos
Que quiero lograr en mi vida ejemplos Clarice lispector o primeiro beijo
Clarice lispector o primeiro beijo Desejo vitor hugo
Desejo vitor hugo Subsistema fraternal
Subsistema fraternal 7 selos do apocalípse
7 selos do apocalípse Triangulo retangulo
Triangulo retangulo Quando duas almas se encontram o que realça primeiro
Quando duas almas se encontram o que realça primeiro Unamos agora os pés e
Unamos agora os pés e Mordeu
Mordeu O primeiro encontro com jesus ressuscitado
O primeiro encontro com jesus ressuscitado Primeiro comando da capital leader
Primeiro comando da capital leader Desejo primeiro que você ame e que amando victor hugo
Desejo primeiro que você ame e que amando victor hugo Hinario novo cantico 231
Hinario novo cantico 231 O que fez maria madalena no primeiro dia da semana
O que fez maria madalena no primeiro dia da semana Projeção ortogonal
Projeção ortogonal Consultas de puericultura no primeiro ano de vida
Consultas de puericultura no primeiro ano de vida Primeiro compilador
Primeiro compilador Purificação e iluminação
Purificação e iluminação Deus em.primeiro lugar
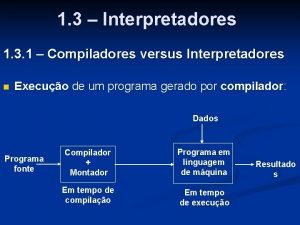
Deus em.primeiro lugar Compilador vs interpretador
Compilador vs interpretador Buscai primeiro o reino de deus
Buscai primeiro o reino de deus Pronomes indefinidos
Pronomes indefinidos Primeiro movimento literário
Primeiro movimento literário Geração 1955
Geração 1955 Reunião de pais catequese
Reunião de pais catequese Indica a classe e subclasse
Indica a classe e subclasse Amamos porque ele nos amou primeiro
Amamos porque ele nos amou primeiro O que é turnover no basquete
O que é turnover no basquete Arte fundamentos conceituais
Arte fundamentos conceituais Fundamentos de la doctrina social de la iglesia
Fundamentos de la doctrina social de la iglesia Fundamentos de la interculturalidad
Fundamentos de la interculturalidad Cuáles son los fundamentos del currículo
Cuáles son los fundamentos del currículo Fundamentos de los dividendos
Fundamentos de los dividendos Fundamentos de la teoria de los colores harald kuppers pdf
Fundamentos de la teoria de los colores harald kuppers pdf Fundamentos de la ebi
Fundamentos de la ebi Fundamentos de la planeacion estrategica
Fundamentos de la planeacion estrategica