Fggvnytranszformcik Ksztette Lesku Katalin IV vfolyam matematika szak

Függvénytranszformációk Készítette: Lesku Katalin IV. évfolyam matematika szak

A függvények és a geometriai transzformáció • Ismerjük a különböző alapfüggvényeket, azok ábrázolását, és a geometriai transzformációkat. • Vajon függvényábrázolás közben találkozhatunk geometriai transzformációkkal is? • Tekintsük a következő függvényábrázolásokat.

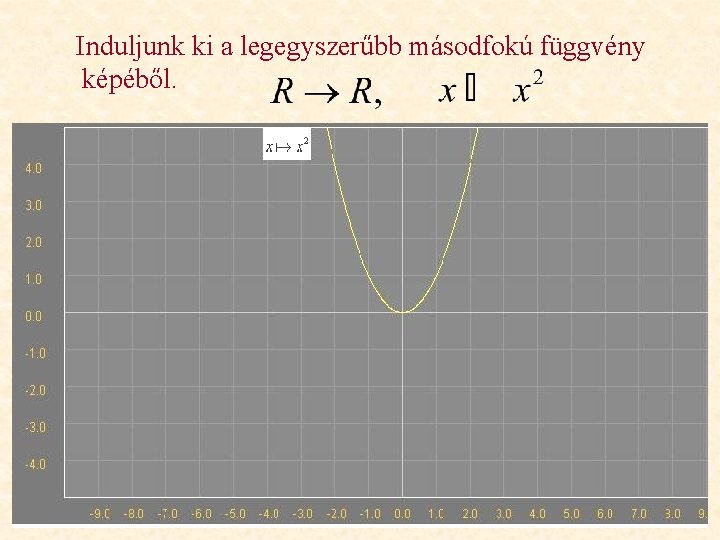
Induljunk ki a legegyszerűbb másodfokú függvény képéből.

Hozzárendelési szabályok • Változtassuk meg a hozzárendelési szabályt, és figyeljük meg a függvény képének változásait! 1. ábra 2. ábra 3. ábra 4. ábra 5. ábra

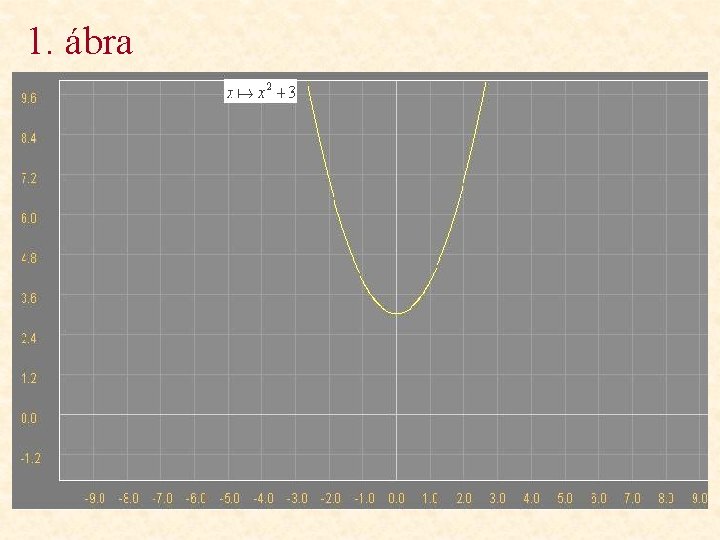
1. ábra

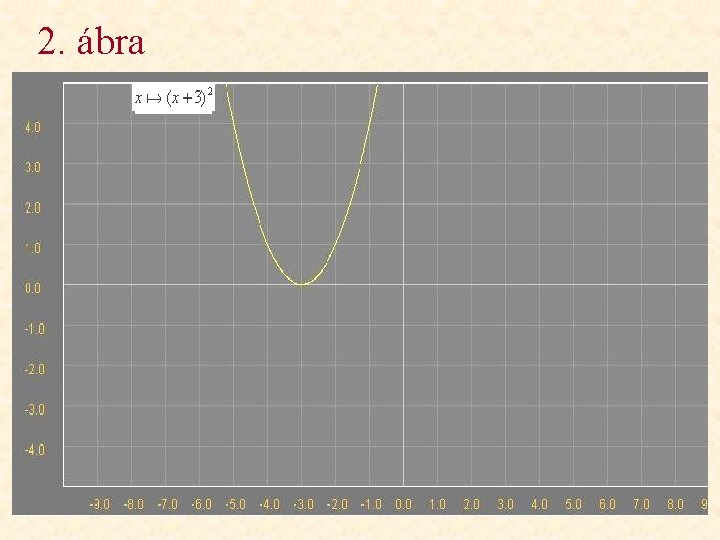
2. ábra

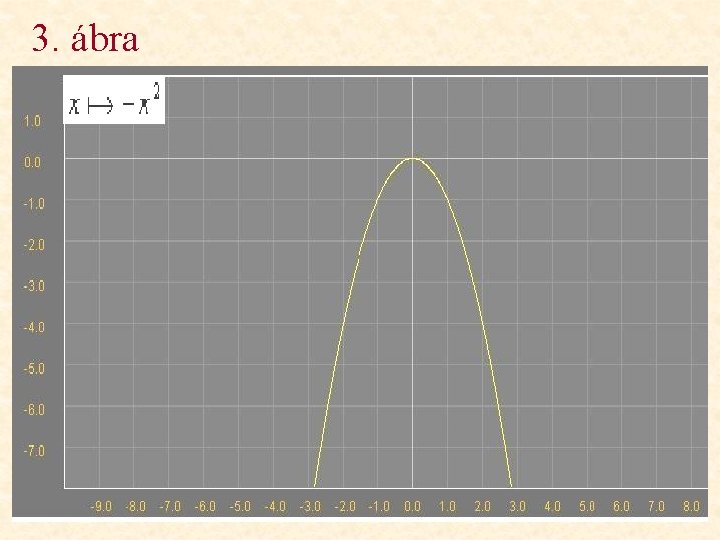
3. ábra

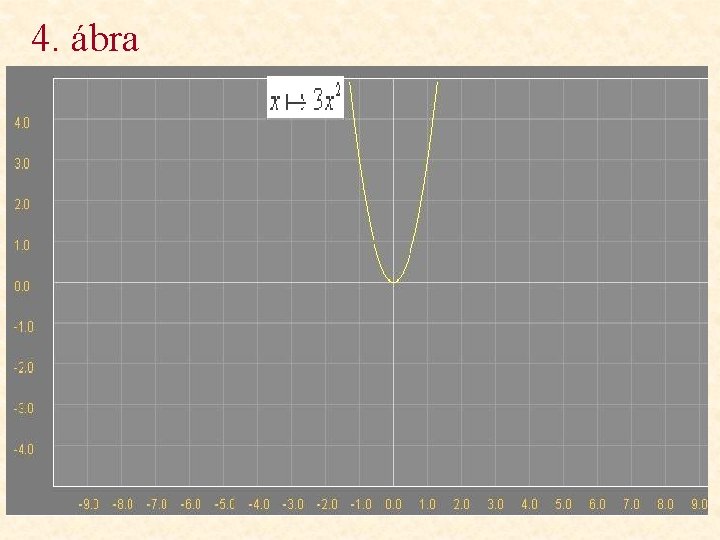
4. ábra

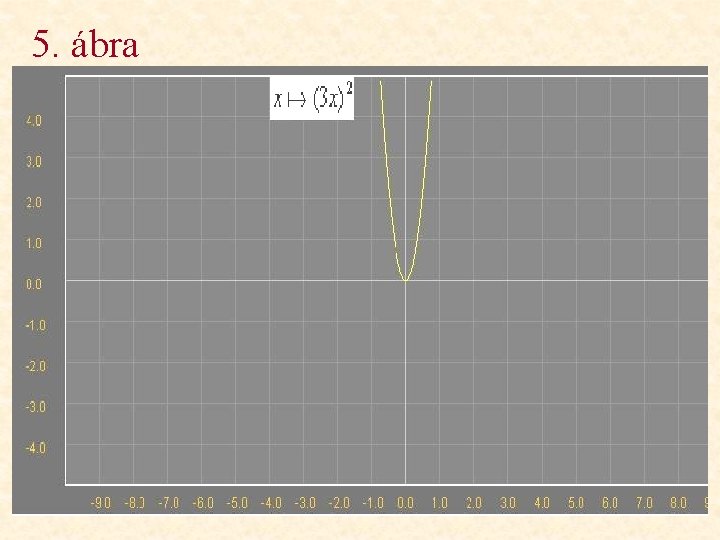
5. ábra

Változások a függvény képében Milyen változásokat figyelhetünk meg? • 1. ábra: a függvény képe az y tengellyel párhuzamosan eltolódik 3 egységgel felfelé. • 2. ábra: a függvény képe az x tengellyel párhuzamosan eltolódik 3 egységgel balra. • 3. ábra: a függvény képe az x tengelyre tükröződik. • 4. ábra: a függvény képe az y tengely irányában 3 -szorosára nyúlik. • 5. ábra: a függvény képe az x tengely irányában 1/3 -szorosára összenyomódik.

Mit állapíthatunk meg? • Az öt példából úgy tűnik, hogy ha egy-egy alapfüggvény hozzárendelési szabályát a fenti módon megváltoztatjuk, akkor az új függvény képét az alapfüggvény képéből valamilyen geometriai transzformációval megkaphatjuk. • Az alapfüggvényeknél a hozzárendelés ilyen jellegű megváltoztatását függvénytranszformációnak nevezzük.

Függvénytranszformációk esetei A függvényérték transzformációi A változó transzformációi f(x)+c f(x+c) –f(x) f(– x) cf(x) 0<c f(cx) 0<c Alapfüggvényünk az f függvény, helyettesítési értéke az x helyen: f(x).

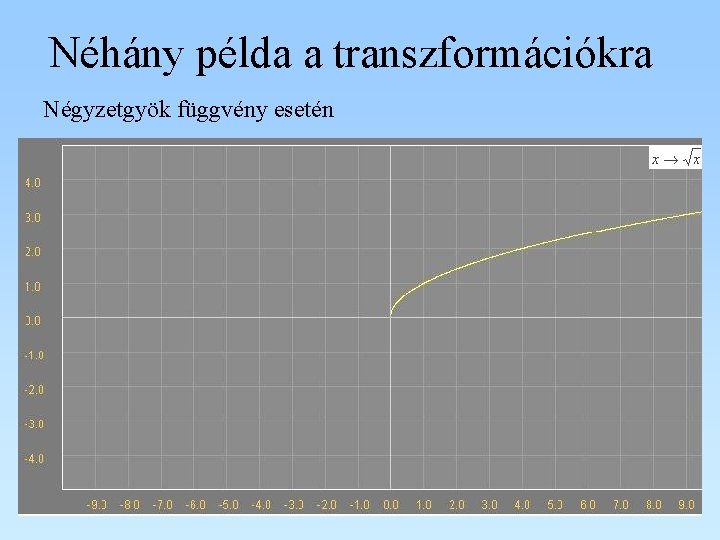
Néhány példa a transzformációkra Négyzetgyök függvény esetén

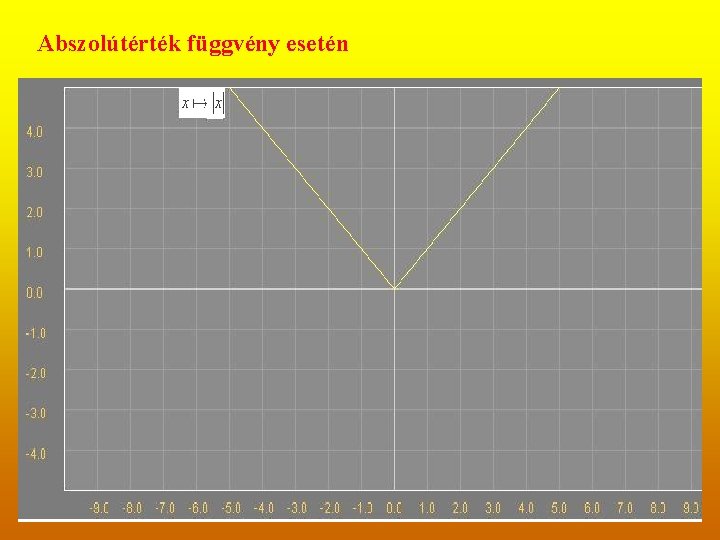
Abszolútérték függvény esetén

Az eredeti függvény grafikonjának változása A függvényérték transzformációi A változó transzformációi f(x)+c: az f függvény képe az y f(x+c): az f függvény képe az x tengellyel párhuzamosan eltolódik |c| -vel, ha 0<c felfelé, ha 0>c lefelé -vel, ha 0<c balra, ha 0>c jobbra -f(x): az f függvény képe az x tengelyre tükröződik f(-x): az f függvény képe az y tengelyre tükröződik cf(x): az f függvény képe az y f(cx): az f függvény képe az x tengely irányában c-szeresére nyúlik, tengely irányában 1/c-szeresére ha 1<c, összenyomódik, ha 0<c<1 összenyomódik, 1<c, nyúlik, ha 0<c<1