Facility Location Logistics Management Factors that Affect Location

Facility Location • Logistics Management • Factors that Affect Location Decisions • Distance Measures • Classification of Planar Facility Location Problems • Planar Single-Facility Location Problems – Minisum Location Problem with Rectilinear Distances – Minisum Location Problem with Euclidean Distances – Minimax Location Problem with Rectilinear Distances – Minimax Location Problem with Euclidean Distances • Planar Multi-Facility Location Problems – Minisum Location Problem with Rectilinear Distances

Logistics Management • Logistics Management can be defined as the management of the transportation and distribution of goods. The term goods includes raw materials or subassemblies obtained from suppliers as well as finished goods shipped from plants to warehouses or customers. • Logistics management problems can be classified into three categories: – Location Problems: involve determining the location of one or more new facilities in one or more of several potential sites. The cost of locating each new facility at each of the potential sites is assumed to be known. It is the fixed cost of locating a new facility at a particular site plus the operating and transportation cost of serving customers from this facility-site combination. – Allocation Problems: assume that the number and location of facilities are known a priori and attempt to determine how each customer is to be served. In other words, given the demand for goods at each customer center, the production or supply capacities at each facility, and the cost of serving each customer from each facility, the allocation problem determines how much each facility is to supply to each customer center. – Location-Allocation Problems: involve determining not only how much each customer is to receive from each facility but also the number of facilities along with their locations and capacities.

Factors that Affect Location Decisions • • • • • Proximity to source of raw materials. Cost and availability of energy and utilities. Cost, availability, skill, and productivity of labor. Government regulations at the federal, state, county, and local levels. Taxes at the federal, state, county, and local levels. Insurance. Construction costs and land price. Government and political stability. Exchange rate fluctuation. Export and import regulations, duties, and tariffs. Transportation system. Technical expertise. Environmental regulations at the federal, state, county and local levels. Support services. Community services - schools, hospitals, recreation, and so on. Weather. Proximity to customers. Business climate. Competition-related factors.

Distance Measures • Rectilinear distance (L 1 norm) Pi = (ai, bi) – d(X, Pi) = |x - ai| + |y - bi| X = (x, y) • Straight line or Euclidean distance (L 2 norm) Pi = (ai, bi) – d(X, Pi) = • Tchebyshev distance (L norm) X = (x, y) Pi = (ai, bi) – d(X, Pi) = max{|x - ai|, |y - bi|} X = (x, y)

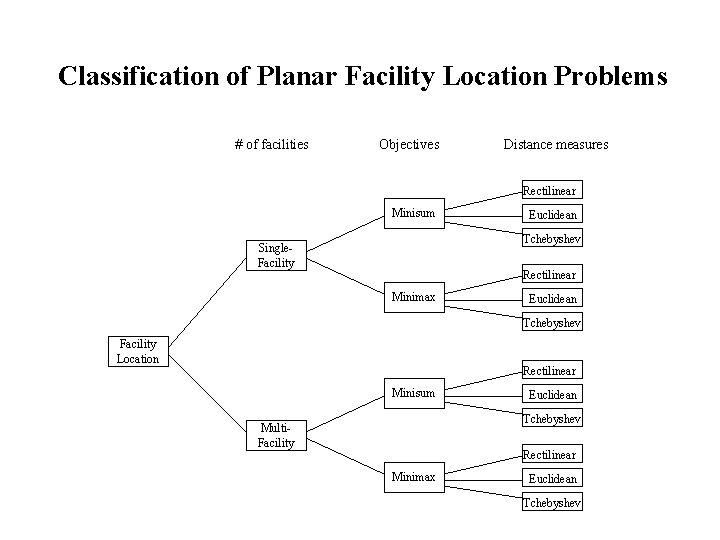
Classification of Planar Facility Location Problems # of facilities Objectives Distance measures Rectilinear Minisum Euclidean Tchebyshev Single. Facility Rectilinear Minimax Euclidean Tchebyshev Facility Location Rectilinear Minisum Euclidean Tchebyshev Multi. Facility Rectilinear Minimax Euclidean Tchebyshev

Planar Single-Facility Location Formulations • Minisum Formulation : Min f(x) = where X = (x, y) : location of the new facility Pi = (ai, bi) : location of the i-th existing facility, i = 1, …, m wi : weight associated to the i-th existing facility For example, wi = , where ci : cost per hour of travel, ti : number of trips per month, vi : average velocity. • Minimax Formulation : Min f(x) = i =Max {wi d(X, Pi)} 1, …, m Min s. t. z wi d(X, Pi) z, i = 1, …, m

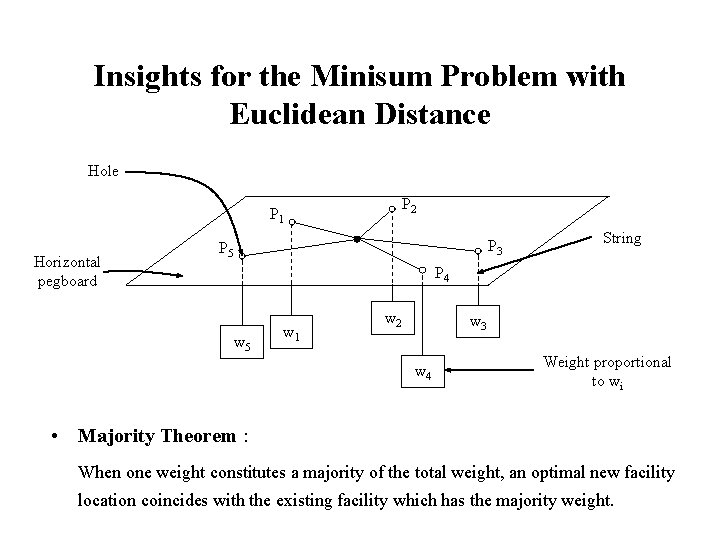
Insights for the Minisum Problem with Euclidean Distance Hole P 2 P 1 Horizontal pegboard P 3 P 5 String P 4 w 5 w 1 w 2 w 3 w 4 Weight proportional to wi • Majority Theorem : When one weight constitutes a majority of the total weight, an optimal new facility location coincides with the existing facility which has the majority weight.

Minisum Location Problem with Rectilinear Distances Min f(x, y) = Note that f(x, y) = f 1(x) + f 2(y) where f 1(x) = f 2(y) = The cost of movement in the x direction is independent of the cost of movement in the y direction, and viceversa. Now, we look at the x direction. f 1(x) is convex a local min is a global min.

Minisum Location Problem with Rectilinear Distances (cont. ) • The coordinates of the existing facilities are sorted so that a 1 a 2 a 3 …. • Now, we consider the case of m = 3. Case x a 1 : f 1(x) = w 1 |a 1 - x| + w 2 |a 2 - x| + w 3 |a 3 - x| = - (w 1 + w 2 + w 3)x + w 1 a 1 + w 2 a 2 + w 3 a 3 = - W x + w 1 a 1 + w 2 a 2 + w 3 a 3 , where W = w 1 + w 2 + w 3 Case a 1 x a 2 : f 1(x) = w 1 |a 1 - x| + w 2 |a 2 - x| + w 3 |a 3 - x| = (w 1 - w 2 - w 3)x - w 1 a 1 + w 2 a 2 + w 3 a 3 = (- W + 2 w 1) x - w 1 a 1 + w 2 a 2 + w 3 a 3 …

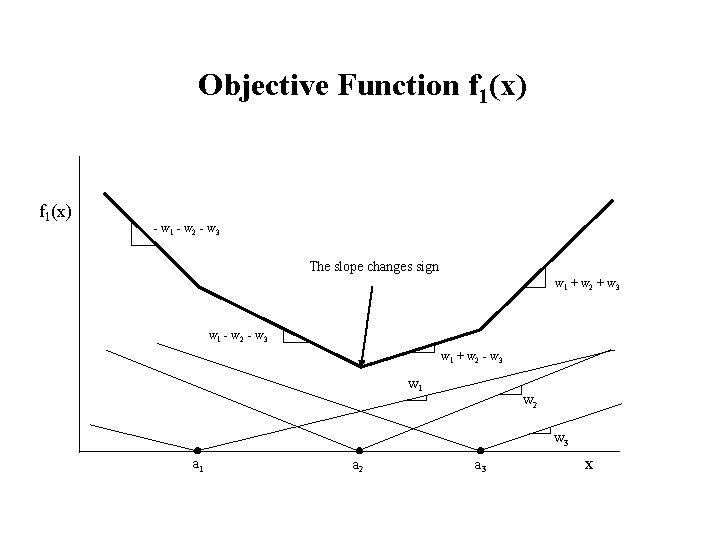
Objective Function f 1(x) - w 1 - w 2 - w 3 The slope changes sign w 1 + w 2 + w 3 w 1 - w 2 - w 3 w 1 + w 2 - w 3 w 1 w 2 w 3 a 1 a 2 a 3 x

Minisum Location Problem with Rectilinear Distances (cont. ) • Slopes of f 1(x) : M 0 = - (w 1 + w 2 + w 3) = - W M 1 = 2 w 1 + M 0 M 2 = 2 w 2 + M 1 M 3 = 2 w 3 + M 2 = w 1 + w 2 + w 3 = W • Median conditions : f 1(x) is minimized at the point where the slope changes from nonpositive to nonnegative. M 1 = w 1 - w 2 - w 3 < 0 2 w 1 < (w 1 + w 2 + w 3) = W w 1 < W/2 M 2 = w 1 + w 2 - w 3 0 2 (w 1 + w 2) (w 1 + w 2 + w 3) = W (w 1 + w 2) W/2

Example 1 • Problem Data : m=3 a 1 = 10 a 2 = 20 a 3 = 40 w 1 = 5 w 2 = 6 w 3 = 4 • Solution : W = w 1 + w 2 + w 3 = 15 W/2 = 7. 5 w 1 = 5 < 7. 5 w 1 + w 2 = 11 > 7. 5 Minimizing point : a 2 = 20

Linear Programming Formulation Min f 1(x) = w 1 |a 1 - x| + w 2 |a 2 - x| + w 3 |a 3 - x| Min z = w 1 (r 1+ s 1) + w 2 (r 2+ s 2) + w 3 (r 3+ s 3), s. t. x - r 1 + s 1 x - r 2 + s 2 x Dual variables = a 1, = a 2, : y 1 : y 2 - r 3 + s 3 = a 3 , : y 3 rj, sj 0, j = 1, 2, 3. • Relationships among variables : sj 0. aj - x = rj - sj , |aj - x| = rj + sj, rj, • If both rj, sj > 0, we can reduce each by j = min {rj, sj}. • This maintains feasibility and reduces z In an optimal solution, at least one of the rj and sj is 0, i. e. , rj sj = 0.

Linear Programming Formulation (cont. ) • Dual Problem : Max g = - a 1 y 1 - a 2 y 2 - a 3 y 3 + (w 1 a 1 + w 2 a 2 + w 3 a 3) s. t. y 1 + y 2 + y 3 = w 1 + w 2 + w 3 = W 0 yj 2 wj, j = 1, 2, 3 Min a 1 y 1 + a 2 y 2 + a 3 y 3 s. t. y 1 + y 2 + y 3 = W 0 yj 2 wj, j = 1, 2, 3 0 y 1 2 w 1 a 1 W • Complementary slackness conditions : 0 < yj* < 2 wj x* = aj 1 0 y 2 2 w 2 a 3 0 y 3 2 w 3 a 1 a 2 a 3 2 W

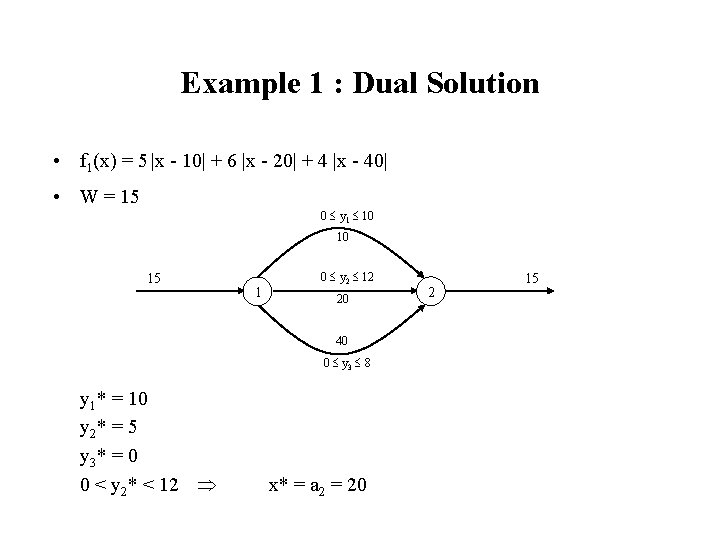
Example 1 : Dual Solution • f 1(x) = 5 |x - 10| + 6 |x - 20| + 4 |x - 40| • W = 15 0 y 1 10 10 15 1 0 y 2 12 20 40 0 y 3 8 y 1* = 10 y 2* = 5 y 3* = 0 0 < y 2* < 12 x* = a 2 = 20 2 15

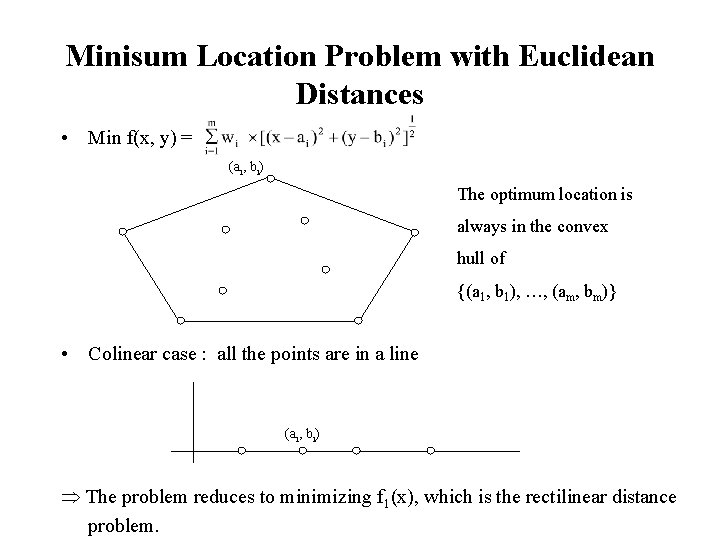
Minisum Location Problem with Euclidean Distances • Min f(x, y) = (ai, bi) The optimum location is always in the convex hull of {(a 1, b 1), …, (am, bm)} • Colinear case : all the points are in a line (ai, bi) The problem reduces to minimizing f 1(x), which is the rectilinear distance problem.

Non-colinear Case • The graph of is a cone (strictly convex function). y contours (ai, bi) x y • f(x, y) = hull is a line segment. (ai, bi, 0) x is strictly convex unless the convex

Non-colinear Case (cont. ) • First order optimality conditions : (x 0, y 0) is optimal • Any point where the partial derivatives are zero is optimal. Let and

Non-colinear Case (cont. ) =0 =0

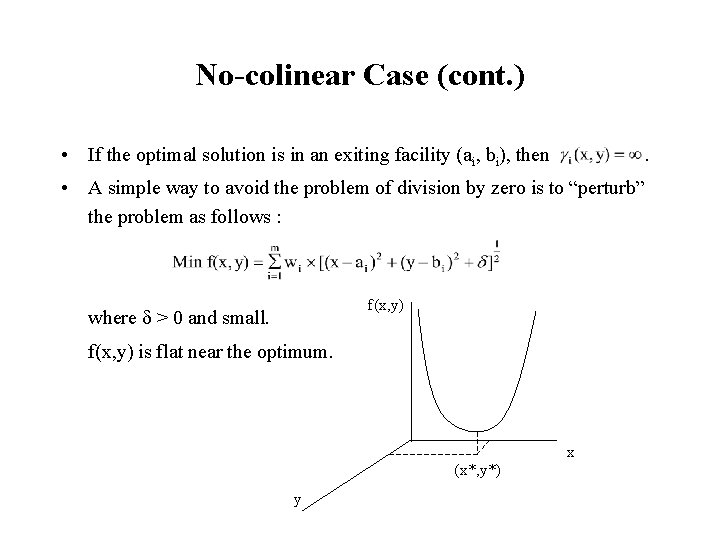
No-colinear Case (cont. ) • If the optimal solution is in an exiting facility (ai, bi), then . • A simple way to avoid the problem of division by zero is to “perturb” the problem as follows : f(x, y) where > 0 and small. f(x, y) is flat near the optimum. x (x*, y*) y

Weiszfeld’s Algorithm Initialization : or Iterative step (k = 1, 2, …) : Terminating conditions : or

Example 2 Problem Data : m=4 P 1 = (0, 0) w 1 = 1 P 2 = (0, 10) w 2 = 1 P 3 = (5, 0) w 3 = 1 P 4 = (12, 6) w 4 = 1 Solution : x 0 = (5+12)/4 = 4. 25 y 0 = (10+6)/4 = 4 k (x, y) f(x, y) 1 4. 023, 3. 116 24. 808 2 3. 949, 2. 647 24. 665 5 3. 958, 2. 124 24. 600 10 3. 995, 2. 011 24. 597 Optimum 4. 000, 2. 000

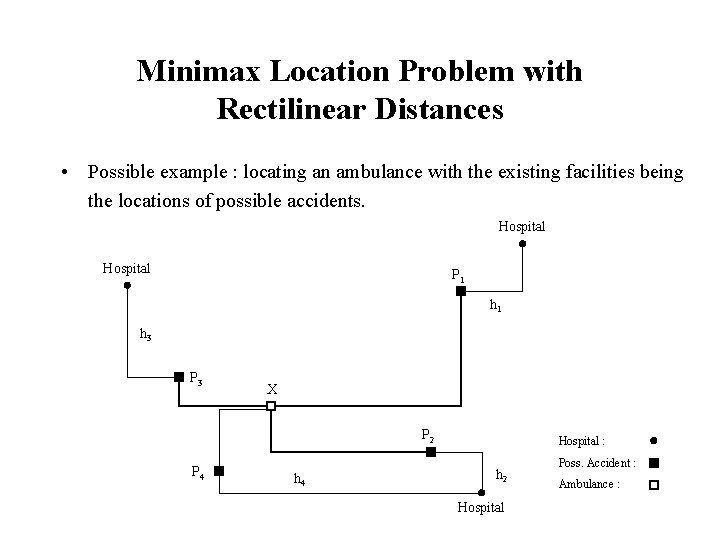
Minimax Location Problem with Rectilinear Distances • Possible example : locating an ambulance with the existing facilities being the locations of possible accidents. Hospital P 1 h 3 P 3 X P 2 P 4 h 4 Hospital : h 2 Hospital Poss. Accident : Ambulance :

Minimax Location Problem with Rectilinear Distances (cont. ) • Notation EF (existing facilities) locations : Pi = (ai, bi), i = 1, …, m NF (new facility = ambulance) location : X = (x, y) Travel distance from EF i to the nearest hospital = hi, i = 1, …, m Travel distance from NF to EF i = |x - ai| + |y - bi| • Formulation : Min where Min s. t. g(x, y) = max {|x - ai| + |y - bi| + hi : i = 1, …, m} z |x - ai| + |y - bi| + hi z, i = 1, …, m

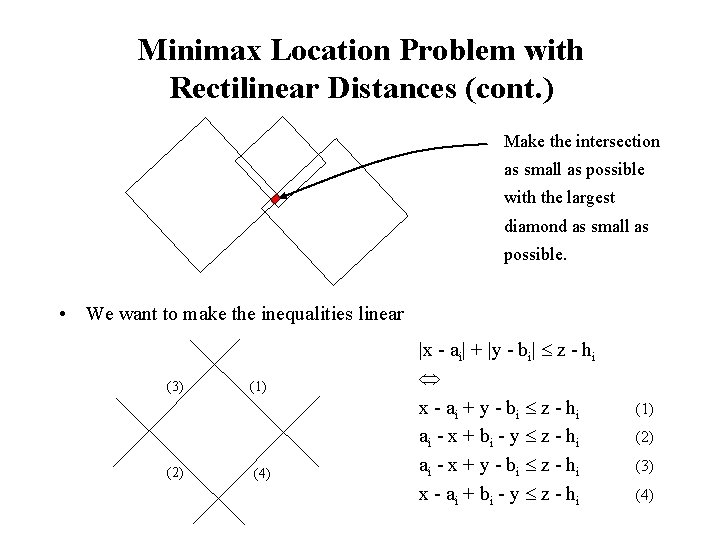
Minimax Location Problem with Rectilinear Distances (cont. ) Make the intersection as small as possible with the largest diamond as small as possible. • We want to make the inequalities linear (3) (2) (1) (4) |x - ai| + |y - bi| z - hi x - ai + y - bi z - hi ai - x + bi - y z - hi ai - x + y - bi z - hi x - ai + bi - y z - hi (1) (2) (3) (4)

Minimax Location Problem with Rectilinear Distances (cont. ) Min z x + y - z ai + bi - hi, s. t. i = 1, . . . , m x + y + z ai + bi + hi, i = 1, . . . , m - x + y - z - ai + bi - hi, i = 1, . . . , m - x + y + z - ai + bi + hi, i = 1, . . . , m Min s. t. z x + y - z c 1 where c 1 = Min {ai + bi - hi} i = 1, . . . , m x + y + z c 2 = Max {ai + bi + hi} - x + y - z c 3 = Min {- ai + bi - hi} - x + y + z c 4 = Max {- ai + bi + hi} i = 1, . . . , m

Minimax Location Problem with Rectilinear Distances (cont. ) Min z s. t. - x - y + z - c 1 x + y + z c 2 x - y + z - c 3 - x + y + z c 4 c 5 = Max {c 2 - c 1, c 4 - c 3} z (c 2 - c 1)/2 (lower bound) z (c 4 - c 3)/2 (lower bound) z = c 5/2 Optimal solution : (x 1, y 1, z 1) = 1/2 (c 1 - c 3, c 1 + c 3 + c 5, c 5) (x 2, y 2, z 2) = 1/2 (c 2 - c 4, c 2 + c 4 - c 5, c 5) The line segment joining (x 1, y 1) and (x 2, y 2) is the set of optimal NF locations

Minimax Location Problem with Euclidean Distances • Examples : helicopter in an emergency unit, radio transmitter (x, y) (ai, bi) EF : (ai, bi), i = 1, …, m NF : (x, y) min g(x, y) where g(x, y) = max {[(x - ai)2 + (y - bi)2]1/2, i = 1, …, m} min z s. t. [(x - ai)2 + (y - bi)2]1/2 z, min z s. t. (x - ai)2 + (y - bi)2 z , i = 1, …, m

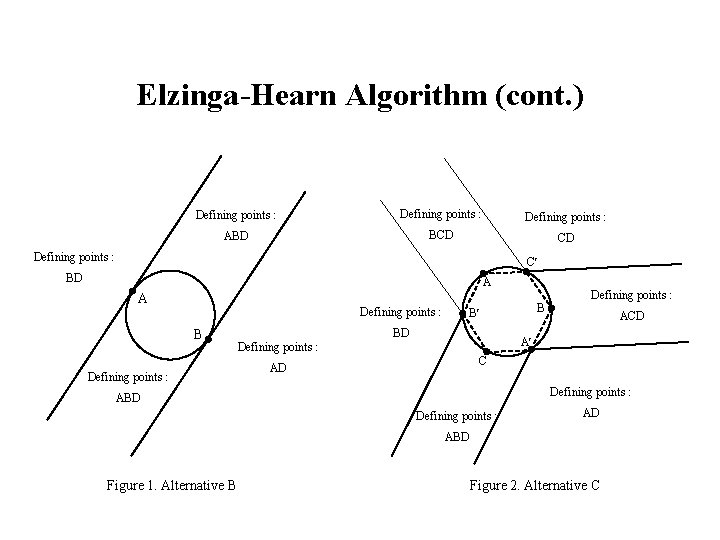
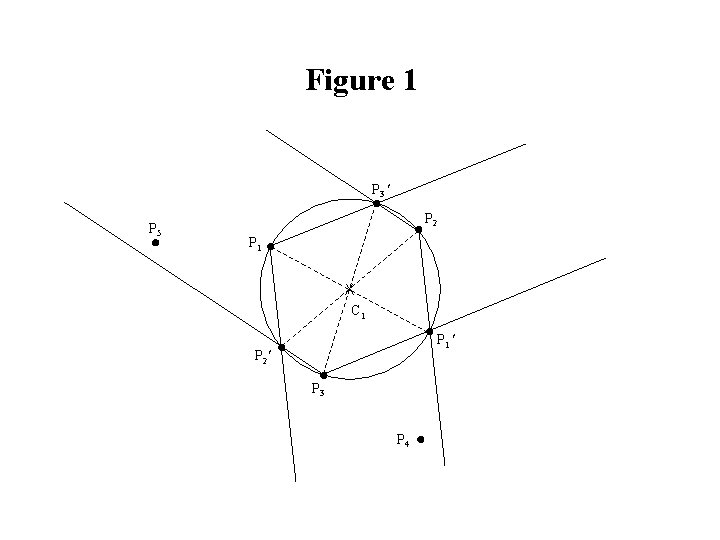
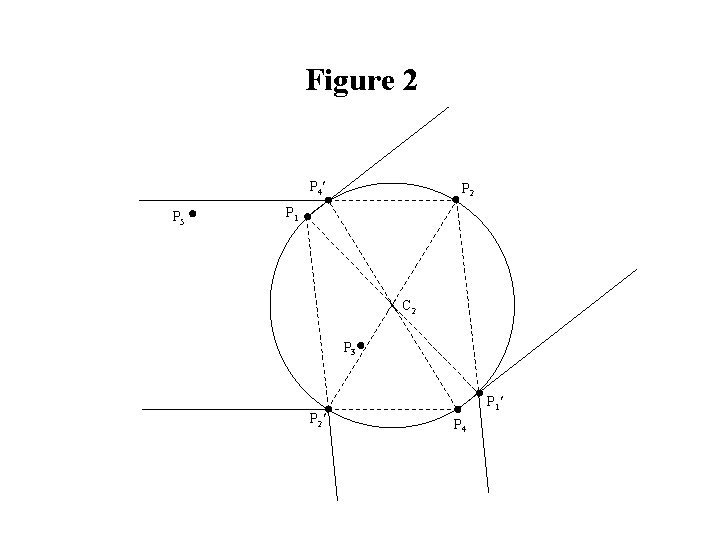
Elzinga-Hearn Algorithm (1971) Step 1. Choose any two points and go to Step 2. Find the minimum covering circle for the chosen points*. Discard from the set of chosen points those points not defining the minimum covering circle, and go to Step 3. If the constructed circle contains all the points, then the center of the circle is a minimax location, so stop. Otherwise, choose some point outside the circle, add it to the set of points defining the circle, and go to Step 2. * Find the minimum covering circle for the chosen points : A. If there are two points, let the two points define the diameter of the circle. B. If there are three points defining a right or obtuse triangle, let the two points opposite to the right or obtuse angle define the diameter of the circle. Otherwise, construct a circle through the three points (see Figure 1). C. If there are four points, construct a circle using as defining points those indicated in Figure 2.

Elzinga-Hearn Algorithm (cont. ) Defining points : ABD BCD CD Defining points : C BD A A Defining points : B Defining points : B B BD ACD A C AD Defining points : ABD Defining points : AD ABD Figure 1. Alternative B Figure 2. Alternative C

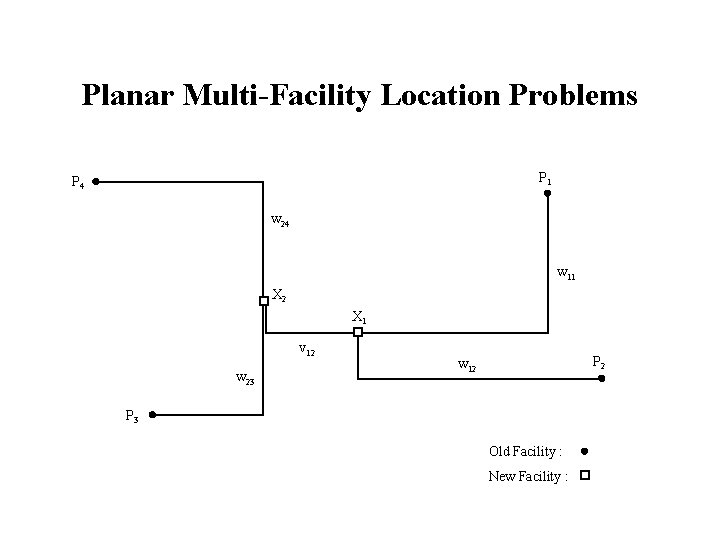
Planar Multi-Facility Location Problems P 1 P 4 w 24 w 11 X 2 X 1 v 12 w 23 P 2 w 12 P 3 Old Facility : New Facility :

Minisum Multi-Facility Location Problem with Rectilinear Distances Location of new facilities: Xj = (xj, yj), j = 1, …, n. Location of existing facilities: Pi = (ai, bi), i = 1, …, m. Weight between new facilities j and k: vjk, where k > j. Weight between new facility j and existing facility i: wji. Problem formulation: Min f((x 1, y 1), …, (xn, yn)) = f 1(x 1, …, xn) + f 2(y 1, …, yn) where f 1(x 1, …, xn) = f 2(y 1, …, yn) =

Example 3 • Problem Data : n = 2 (NF) m = 3 (EF) v = [vjk] = w = [wji] = x = [xj] = (x 1, x 2) a = [aj] = (10, 20, 40) Min f 1(x 1, x 2) = 2 |x 1 - x 2| + 2 |x 1 - 10| + |x 1 - 20| Min f 1(x 1, x 2) = 2 (p 12 + q 12) + 2 (r 11 + s 11) + (r 12 + s 12) s. t. + 4 |x 2 - 20| + 4 (r 21 + s 21) + 5 (r 23 + s 23) x 1 - x 2 - p 12 + q 12 x 1 =0 - r 11 + s 11 x 1 = 10 - r 12 + s 12 x 2 = 20 - r 21 + s 21 x 2 • + 5 |x 2 - 40| = 10 - r 23 + s 23 Relationships among variables : x 1 - x 2 = p 12 - q 12, |x 1 - x 2| = p 12 + q 12, p 12, q 12 0 xi - aj = rij - sij, |xi - aj| = rij + sij, rij, sij 0 = 40

Example 3 (Dual Problem) Max (- 10 u 11 - 20 u 12 - 10 u 21 - 40 u 23) + (10 2 + 20 1 + 10 4 + 40 5) Min 10 u 11 + 20 u 12 + 10 u 21 + 40 u 23 s. t. z 12 + u 11 + u 12 - z 12 =5 + u 21 0 z 12 4 0 u 11 4 0 u 12 2 0 u 21 8 0 u 23 10 + u 23 =7

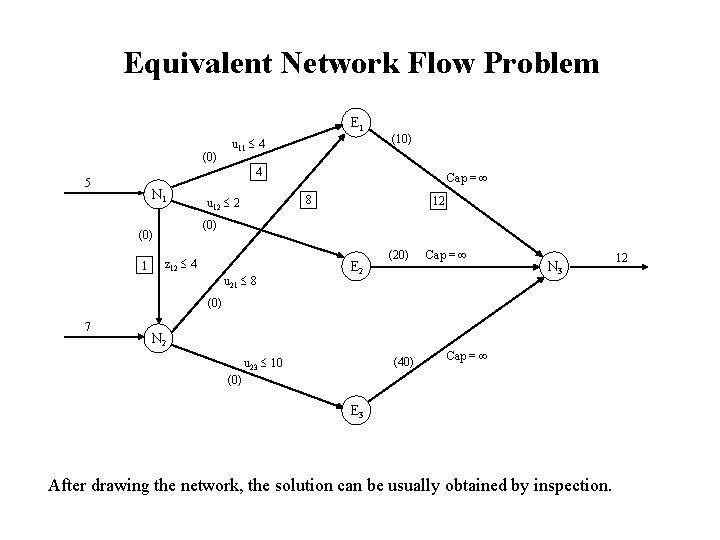
Equivalent Network Flow Problem E 1 (0) u 11 4 (10) 4 5 N 1 8 u 12 2 12 (0) 1 Cap = z 12 4 u 21 8 E 2 (20) Cap = N 3 (0) 7 N 2 u 23 10 (40) Cap = (0) E 3 After drawing the network, the solution can be usually obtained by inspection. 12

Equivalent Network Flow Problem (cont. ) Complementary slackness conditions : 1. xk* xj* zjk* < 2 vjk xj* xk* 0 < zjk* In particular, 0 < zjk* < 2 vjk xj* = xk* 2. ai xj* uji* < 2 wji xj* ai 0 < uji* In particular, 0 < uji* < 2 wji xj* = ai In Example 3, 0 < z 12* < 2 v 12 x 1* = x 2*, 0 < u 12 = 2 w 12 x 2* = a 1 = 10. If the network is not connected, then the problem decomposes into independent problems, one for each component.

Example 4 Four hospitals located within a city are cooperating to establish a centralized blood-bank facility that will serve the hospitals. The new facility is to be located such that the (total) distance traveled is minimized. The hospitals are located at the following coordinates: P 1=(5, 10), P 2=(7, 6), P 3=(4, 2), and P 4=(16, 3). The number of deliveries to be made per week between the blood-bank facility and each hospital is estimated to be 3, 8, 2, and 10, respectively. Assuming rectilinear travel, determine the optimum location. m=4 P 1 = (5, 10) P 3 = (4, 2) Computation of x*: a 3 = 4 a 1 = 5 a 2 = 7 a 4 = 16 Computation of y*: b 3 = 2 b 4 = 3 b 2 = 6 b 1 = 10 w 1 = 3 w 3 = 2 P 2 = (7, 6) P 4 = (16, 3) w 2 = 8 w 4 = 10 w 3 = 2 w 1 = 3 w 2 = 8 w 4 = 10 w 3 = 2 w 3 + w 1 = 5 w 3 + w 1 + w 2 = 13 x* = w 3 = 2 w 4 = 10 w 2 = 8 w 1 = 3 w 3 = 2 w 3 + w 4 = 12 y* = W=

Example 5 (10, 16) 16 h 4 = 11 Find the optimal location of an ambulance with respect to four (known) possible accident locations which coordinates are P 1=(6, 11), P 2=(12, 5), P 3=(14, 7), and P 4=(10, 16). The objective is to minimize 14 12 (6, 11) the maximum distance from the ambulance location to an accident location and from 10 h 1 = 10 (12, 9) the accident location to its closest hospital. The distances from the accident locations 8 to their closest hospitals are h 1=10, h 2=16, h 3=14, and h 4=11. Assume that distances are rectilinear. If multiple optima exist, (14, 7) (10, 7) 6 h 3 = 14 (12, 5) find all optimal solutions. h 2 = 16 (5, 4) 6 8 10 12 14

Example 5 Solution m=4 P 1 = (6, 11) P 3 = (14, 7) h 1 = 10 h 3 = 14 P 2 = (12, 5) P 4 = (10, 16) h 2 = 16 h 4 = 11 c 1 = min {ai + bi - hi} = min {6+11 -10, 12+5 -16, 14+7 -14, 10+16 -11} = c 2 = max {ai + bi + hi} = max {6+11+10, 12+5+16, 14+7+14, 10+16+11} = c 3 = min {-ai + bi - hi} = min {-6+11 -10, -12+5 -16, -14+7 -14, -10+16 -11} = c 4 = max {-ai + bi + hi} = max {-6+11+10, -12+5+16, -14+7+14, -10+16+11} = c 5 = max (c 2 - c 1, c 4 - c 3}= max { - , - }= Optimal objective value: z* = Set of optimal solutions: line segment defined by the following end points: (x 1*, y 1*) = (c 1 - c 3, c 1 + c 3 + c 5) = ( - , + + (x 2*, y 2*) = (c 2 - c 4, c 2 + c 4 - c 5) = ( - , + - )=( , , ) )

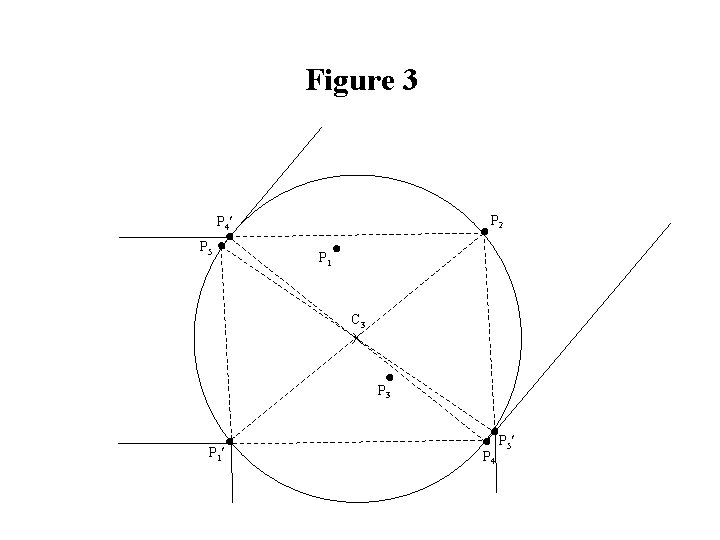
Example 6 Given five existing facilities located at points P 1, P 2, P 3, P 4, and P 5 as shown below, determine the optimum location for a new facility which will minimize the maximum distance to the existing facilities. Assume that distances are Euclidean. Elzinga-Hearn algorithm: Figure 1 : Initial set of points = {P 1, P 2, P 3}; center = C 1. Figure 2 : 2 nd set of points = {P 1, P 2, P 4}; center = C 2. Figure 3 : 3 rd set of points = {P 2, P 4, P 5}; center = C 3 (optimal location).

Figure 1 P 3 P 5 P 2 P 1 C 1 P 1 P 2 P 3 P 4

Figure 2 P 4 P 5 P 2 P 1 C 2 P 3 P 2 P 1 P 4

Figure 3 P 4 P 5 P 2 P 1 C 3 P 1 P 4 P 5