Experiment 19 Hermit and Socializer a Analyze the

Experiment 19: Hermit and Socializer a) Analyze the role which pre-play communication plays in this game? What message should the Hermit send, with respect to what he plans to do? How should the Socializer react to that message? b) Ignoring the pre-play communication, derive all pure strategy Nash equilibria of the one-shot game, using the Normal form. © WU IMS 1

Experiment 19: Hermit and Socializer Forest Lake § Pre-play communication? § If the choice of the Hermit 20 -20 Forest -20 20 is correlated with his Hermit message (i. e. in any way -20 20 Lake dependent on it), then 20 -20 the Socializer always has a best reply, which is bad for the Hermit. § Thus, the choice of the Hermit should be uncorrelated to his message. As a result, pre-play communication is meaningless, „cheap talk”, and the Socializer should not react to it. § Nash equilibria? § There is no equilibrium in pure strategies: none of the four situations is stable, in each one player has an incentive to deviate. © WU IMS 2

Experiment 19: Hermit and Socializer c) Assume that the Hermit could play a “randomized” strategy in which he chooses “Forest” with a probability of P% and “Lake” with a probability of 100%-P%. • Now, for the probabilities of P=30%, P=50%, and P=70%, check what the best answer(s) of the Socializer would be. Would, in turn, the Hermit’s chosen P% also be the best answer (or one of the best answers) to the Socializer’s best answer? • Do the same analysis for the “Socializer”, who might choose “forest” with probability Q% and “Lake” with probability 100%-Q%. • Can you state a Nash equilibrium in which both players choose a P% and Q% such that their “randomized” strategies are best answers to each other? 3 © WU IMS

Experiment 19: Hermit and Socializer Forest Lake Forest Hermit Lake -20 20 20 -20 -20 20 § Both players have the possibility to choose a strategy which chooses randomly from the available pure strategies given some probability distribution. § In Nash equilibrium, beliefs are right. § Thus, we are looking for a situation where each chooses a strategy where he cannot do better given the other‘s strategy, but still the other correctly expects this strategy. © WU IMS 4

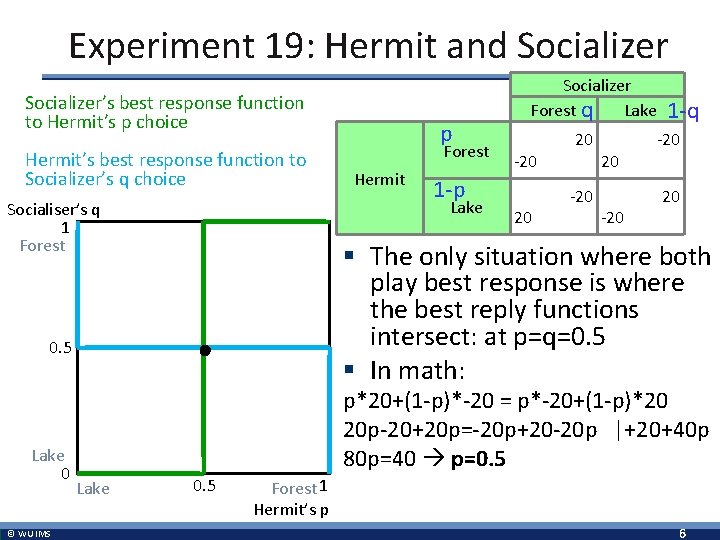
Experiment 19: Hermit and Socializer § In a mixed strategy, a Forest q Lake 1 -q player chooses a p 20 -20 probability distribution Forest -20 20 over his pure strategies. Hermit 1 -p -20 20 § Now, say Hermit plays a Lake 20 -20 mixed strategy p to which the Socializer prefers to choose Forest over Lake. Then, Hermit will expect him choosing Forest, so Hermit’s best answer is not a mix anymore, it is pure Lake. § Thus, the only stable situation is where the Socializer is indifferent between choosing Lake and Forest, given the Hermit’s mixed strategy. This is also true vice versa: the Hermit needs to be indifferent with respect to the Socializer’s strategy in a stable mixed strategy situation. § In other words: each player wants to keep the other player guessing about his action. © WU IMS 5

Experiment 19: Hermit and Socializer’s best response function to Hermit’s p choice Hermit’s best response function to Socializer’s q choice Hermit -20 1 -p 20 20 -20 1 -q -20 20 § The only situation where both play best response is where the best reply functions intersect: at p=q=0. 5 § In math: 0. 5 © WU IMS Forest Lake Socialiser’s q 1 Forest Lake 0 p Socializer Forest q Lake p*20+(1 -p)*-20 = p*-20+(1 -p)*20 20 p-20+20 p=-20 p+20 -20 p |+20+40 p 80 p=40 p=0. 5 Lake 0. 5 Forest 1 Hermit’s p 6

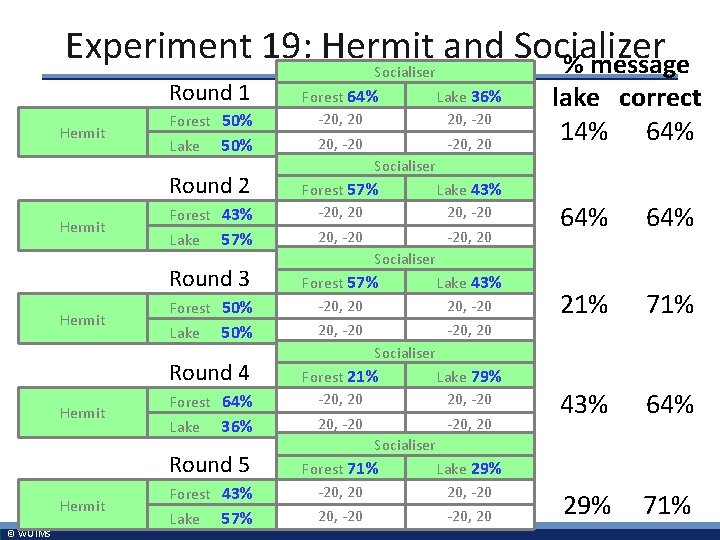
Experiment 19: Hermit and Socializer § Data d) Analyze the data set of experiment 19. Specifically, look at how individual participants play over the rounds. How does that relate to the results from your analysis under c)? © WU IMS 7

Experiment 19: Hermit and Socializer % message Round 1 Hermit Forest 50% Lake 50% Round 2 Hermit Forest 43% Lake 57% Round 3 Hermit Forest 50% Lake 50% Round 4 Hermit Forest 64% Lake 36% Round 5 Hermit © WU IMS Forest 43% Lake 57% Socialiser Forest 64% -20, 20 Lake 36% 20, -20 -20, 20 lake correct 14% 64% Socialiser Forest 57% -20, 20 Lake 43% 20, -20 -20, 20 64% 21% 71% 43% 64% 29% 71% Socialiser Forest 57% -20, 20 Lake 43% 20, -20 -20, 20 Socialiser Forest 21% -20, 20 Lake 79% 20, -20 -20, 20 Socialiser Forest 71% -20, 20 Lake 29% 20, -20 -20, 20

P ID As As Message Hermit Socializer as Hermit Experiment 19: Hermit and Socializer § Individual behavior over rounds lake: forest § Participants seem to randomize (only 3 rounds observed ): • 79% switch at least once within a role • 50% sent the wrong message at least once as hermit © WU IMS 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 1: 2 1: 0 2: 0 1: 3 2: 3 0: 4 2: 1 1: 0 1: 3 0: 1 3: 0 0: 2 1: 1 2: 1 1: 0 1: 2 2: 1 2: 3 2: 2 1: 0 2: 1 0: 0 0: 1 2: 0 2: 2 1: 0 0: 1 1: 1 0: 4 0: 1 3: 1 1: 2 0: 2 4: 0 2: 0 0: 3 1: 1 0: 0 0: 1 4: 0 1: 1 2: 0 3: 2 1: 1 2: 3 4: 0 3: 0 1: 0 2: 2 4: 1 2: 2 2: 1 1: 0 4: 0 0: 1 3: 0 1: 1 2: 1 1: 0 1: 2 2: 0 2: 1 2: 3 1: 0 2: 1 3: 0 0: 0 1: 2 0: 0 0: 19

Mixed strategies § Mixed strategy: player chooses a probability distribution over his pure strategies. • plays each of his pure strategies with a certain probability. § Mixed strategy Nash equilibrium: • combination of all players’ probability distributions over pure strategies • such that no player has an incentive to play a different probability distribution. © WU IMS 10

Mixed strategies § Necessary condition to play a mixed strategy: • players must be indifferent between their pure strategies (which they play with positive probability) • because if one pure strategy is better than others, they would choose that pure strategy with 100% and not mix. § Thus, in a (purely) mixed-strategy Nash equilibrium, • each player chooses a mixed strategy such that the other player is indifferent which pure strategy to choose, • and therefore will play a mixed strategy, too. § Thus, this is how we solve for a mixed strategy equilibrium: • For each player we are looking for the mixed strategy which sets the other players indifferent between their pure strategies. © WU IMS 11

Experiment 18: Chicken § 2 pure strategy Nash equilibria • Straight, Swerve • Swerve, Straight Driver 1 p Swerve Driver 2 q Swerve Straight 1 -q 0 1 -p Straight 20 0 -20 -100 § But there is also a mixed-strategy equilibrium. § Now assume than one driver swerves with probability p, and the other driver swerves with probability q. § For which p and q is this an equilibrium? © WU IMS 12

Experiment 18: Chicken § 2 pure strategy Nash equilibria • Straight, Swerve • Swerve, Straight Driver 1 p Swerve Driver 2 q Swerve Straight 1 -q 0 1 -p Straight 20 0 -20 -100 § When we play a mixed strategy, and he prefers one over the other, then he will purely play the one he prefers, which also brings us back to our pure strategy best response. Thus, we have to set him indifferent. This applies to both drivers (symmetric game). § The other is indifferent if p*0 + (1 -p)*-20 = p*20 + (1 -p)*-100 § -20+20 p=20 p-100+100 p 80 = 100 p p=8/10 q=8/10 § Thus, in a symmetric mixed strategy Nash equilibrium, both drivers swerve with a probability of 80%. Nobody has an incentive to deviate, as they are indifferent between Swerve and Straight. © WU IMS 13

Experiment 18: Chicken Driver 2’s best response function to Driver 1’s p choice Driver 1’s best response function to Driver 2’s q choice Driver 2’s q 1 Swerve p Swerve Driver 1 © WU IMS 0 1 -p Straight 20 0 -20 -100 § There are three equilibria: • p=0, q=1 • p=1, q=0 • p=0. 8, q=0. 8 0. 5 Straight 0 Driver 2 q Swerve Straight 1 -q Straight 0. 5 Swerve 1 Driver 1’s p 14

Hawk and Dove § 2 pure strategy Nash equilibria Bird 2 Hawk 1 -p • Dove, Hawk p Dove p • Hawk, Dove V/2 V Dove V/2 0 § But none of the pure strategies is Bird 1 “evolutionary stable”: If the 1 -p 0 (V-C)/2 Hawk whole population would be V (V-C)/2 Hawks, a Dove mutation would be quite successful, relatively, and therefore proliferate. § In a mixed equilibrium, as in an evolutionary stable equilibrium, there must be no strategy available which performs better against the population than the current population indifference § Let p be the share of Doves, and (1 -p) the share of Hawks. Then: § p*V/2 + (1 -p)*0 = p*V + (1 -p)*(V-C)/2 p = 1 -V/C § The evolutionary stable proportion of Hawks and Doves is V/C to 1 -V/C. That is, the higher the value of resource V and the lower costs of fighting, the more Hawks. If V>C, all will be Hawks (and we got ourselves an evolutionary prisoner’s dilemma). © WU IMS 15

Experiment 17: Battle of the Sexes § 2 pure strategy Nash equilibria: • Opera, Opera • Football, Football p Opera fan goes to Opera 1 -p Football fan goes to q Opera Football 1 -q 30 20 0 10 10 30 § Assume that the Opera fan 0 20 plays Opera with probability p, and Football with probability (1 -p). Similar, Football fan plays Opera with q, and Football with (1 -q). § Now, we know that if I play a strategy where the other is not indifferent between both pure strategies, he will choose one of them. So the condition is to set him indifferent. § Opera fan tries to set Football fan indifferent, such that p*20+(1 -p)*0=p*10+(1 -p)*30 20 p=10 p+30 -30 p 40 p=30 p= ¾ § Football fan tries to set Opera fan indifferent such that q*30+(1 -q)*10=q*0+(1 -q)*20 30 q+10 -10 q=20 -20 q 40 q=10 q= ¼ § In the mixed NE, both choose their favorite in 75% of the cases. © WU IMS Football 16

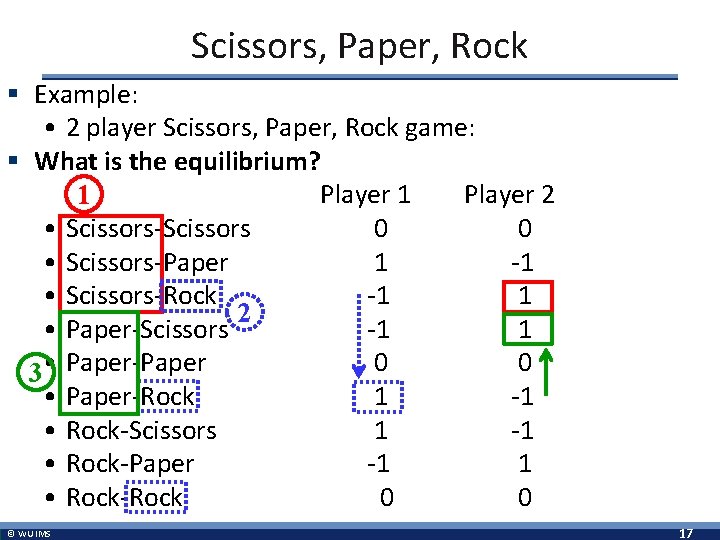
Scissors, Paper, Rock § Example: • 2 player Scissors, Paper, Rock game: § What is the equilibrium? Player 1 Player 2 1 • Scissors-Scissors 0 0 • Scissors-Paper 1 -1 • Scissors-Rock -1 1 2 • Paper-Scissors -1 1 0 0 3 • Paper-Paper • Paper-Rock 1 -1 • Rock-Scissors 1 -1 • Rock-Paper -1 1 • Rock-Rock 0 0 © WU IMS 17

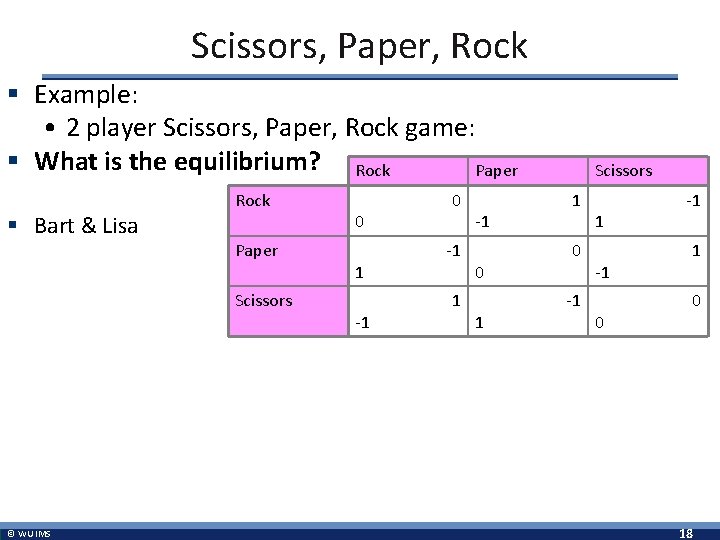
Scissors, Paper, Rock § Example: • 2 player Scissors, Paper, Rock game: § What is the equilibrium? Rock Paper § Bart & Lisa Rock Paper Scissors © WU IMS 0 1 -1 0 -1 1 -1 0 1 Scissors 1 0 -1 1 -1 0 -1 1 0 18

Scissors, Paper, Rock § Example 1: • 2 player Scissors, Paper, Rock game: § What is the equilibrium? Rock Paper § Bart & Lisa § Mixed Equilibrium: § § Rock p Paper q Scissors 1 -p-q 0 1 -1 0 -1 1 -1 0 1 Scissors 1 0 -1 1 -1 0 -1 1 0 p*0+q*-1+(1 -p-q)*1 = p*1 + q*0 + (1 -p-q)*-1 = p*-1 + q*1 + (1 -p-q)*0 -2 q+1 -p = 2 p -1+q = -p + q 3 p =1 p=1/3 -2 q+1 -p = -p + q -3 q = -1 q=1/3 (1 -p-q)=1/3 § A game of pure luck: play randomly Rock, Paper, Scissors … © WU IMS 19