Dynamic Programming Algorithm Design Techniques We will cover

Dynamic Programming

Algorithm Design Techniques We will cover in this class: ◦ Greedy Algorithms ◦ Divide and Conquer Algorithms ◦ Dynamic Programming Algorithms ◦ And Backtracking Algorithms These are 4 common types of algorithms used to solve problems. ◦ For many problems, it is quite likely that at least one of these methods will work.

Dynamic Programming Intro We have looked at several algorithms that involve recursion. In some situations, these algorithms solve fairly difficult problems efficiently ◦ BUT in other cases they are inefficient because they recalculate certain function values many times. The example of this given in the text is the Fibonacci example.

Dynamic Programming Intro The Recursive solution to finding the nth Fibonacci number: public static int fibrec(int n) { if (n < 2) return n; else return fibrec(n-1)+fibrec(n-2); } The problem: ◦ Lots and lots of calls to Fib(1) and Fib(0) are made. It would be nice if we only made those method calls once, then simply used those values as necessary. If I asked you to compute the 10 th Fibonacci number, you would never do it using the recursive steps above. Instead, you'd start making a chart:

Dynamic Programming The idea of dynamic programming is to avoid making redundant method calls ◦ Instead, one should store the answers to all necessary method calls in memory and simply look these up as necessary. Using this idea, we can code up a dynamic programming solution to the Fibonacci number question that is far more efficient than the recursive version: public static int fib(int n) { int[] fibnumbers = new int[n+1]; fibnumbers[0] = 0; fibnumbers[1] = 1; for (int i=2; i<n+1; i++) fibnumbers[i] = fibnumbers[i-1]+fibnumbers[i-2]; return fibnumbers[n]; }

Dynamic Programming The only requirement this program has that the recursive one doesn't is the space requirement of an entire array of values. ◦ (But, if you think about it carefully, at a particular moment in time while the recursive program is running, it has at least n recursive calls in the middle of execution all at once. The amount of memory necessary to simultaneously keep track of each of these is in fact at least as much as the memory the array we are using above needs. ) Usually however, a dynamic programming algorithm presents a time-space trade off. ◦ More space is used to store values, ◦ BUT less time is spent because these values can be looked up. Can we do even better (with respect to memory) with our Fibonacci method above? What numbers do we really have to keep track of all the time?

Dynamic Programming To see an illustration of the difference in speed, Arup wrote a short main to test this: public static void main(String[] args) { long start = System. current. Time. Millis(); System. out. println("Fib 30 = "+fib(30)); long mid = System. current. Time. Millis(); System. out. println("Fib 30 = "+fibrec(30)); long end = System. current. Time. Millis(); System. out. println("Fib Iter Time = "+(mid-start)); System. out. println("Fib Rec Time = "+(end-mid)); } Output: ◦ Fib Iter Time = 4 ◦ Fib Rec Time = 258

Longest Common Subsequence Problem The problem is to find the longest common subsequence in 2 given strings. A subsequence of a string is simply some subset of the letters in the whole string in the order they appear in the string. ◦ For example, given the string “GOODMORNING” ◦ “ODOR” is a subsequence made up of the characters at indices 1, 3, 5, and 6. ◦ “MOOD” is not a subsequence, since the characters are out of order.

Longest Common Subsequence Recursive solution to the problem: ◦ If the last characters of both strings s 1 and s 2 match, example, then the LCS = 1 + the LCS of. For both of the“BIRD” strings with their last characters removed. and “FIND” ◦ If the last characters of both strings do NOT For example, “BIR” and “FIN” match, then the LCS will be one of two options: 1)The LCS of x and y without its last character. 2)The LCS of y and x without its last character. Maxtake ( LCS(“BI” “FIN”) , LCS(“BIR” , “FI”) ) ◦ We will then the , maximum of the 2 values. (Also, we could just have easily compared the first 2

public static int lcsrec(String x, String y) { // If one of the strings has 1 character, search for that // character in the other string and return 0 or 1. if (x. length() == 1) return find(x. char. At(0), y); if (y. length() == 1) return find(y. char. At(0), x); // Solve the problem recursively. // Check if corresponding last characters match. if (x. char. At(len 1 -1) == y. char. At(len 2 -1)) return 1 + lcsrec(x. substring(0, x. length()-1), y. substring(0, y. length()-1)); // Corresponding characters do not match. else return max(lcsrec(x, y. substring(0, y. length()-1)), lcsrec(x. substring(0, x. length()-1), y)); }

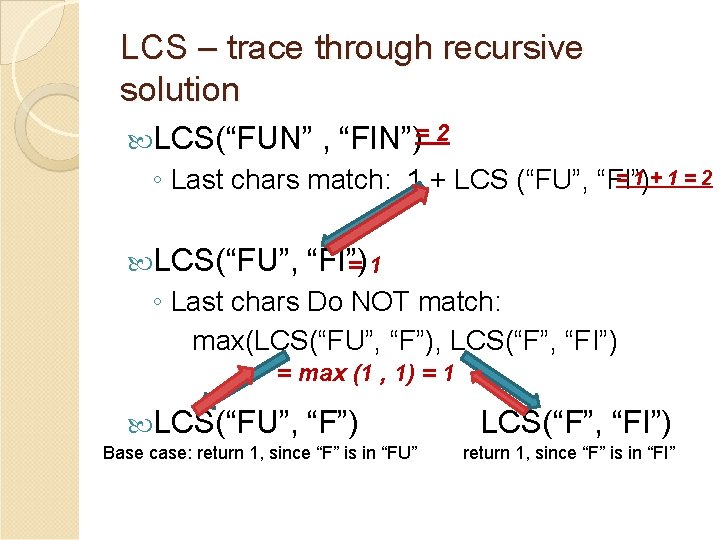
LCS – trace through recursive solution LCS(“FUN” , “FIN”)= 2 =1+1=2 ◦ Last chars match: 1 + LCS (“FU”, “FI”) LCS(“FU”, “FI”) =1 ◦ Last chars Do NOT match: max(LCS(“FU”, “F”), LCS(“F”, “FI”) = max (1 , 1) = 1 LCS(“FU”, “F”) Base case: return 1, since “F” is in “FU” LCS(“F”, “FI”) return 1, since “F” is in “FI”

Longest Common Subsequence Now, our goal will be to take this recursive solution and build a dynamic programming solution. ◦ The key here is to notice that the heart of each recursive call is the pair of indexes, telling us which prefix string we are considering. ◦ In some sense, we can build the answer to "longer" LCS questions based on the answers to smaller LCS questions. ◦ This can be seen in a trace through the recursion at the very last few steps.

Longest Common Subsequnce If we make the recursive call on the strings RACECAR and CREAM, ◦ once we have the answers to the recursive calls for inputs RACECAR and CREA and the inputs RACECA and CREAM, ◦ we can use those two answers and immediately take the maximum of the two to solve our problem!

Longest Common Subsequence Thus, think of storing the answers to these recursive calls in a table, such as this: R C R E A M In A C E C A R XXX this chart for example, the slot with the XXX will store an integer that represents the longest common subsequence of CREA and RAC. (In this case 2. )

Longest Common Subsequence To build the table, first initialize the first row and column. ◦ Basically, we search for the first letter in the other string, when we get there, we put a 1, and all other values subsequent to that on the row or column are also one. ◦ This corresponds to the base case in the recursive code. C R E A M R 0 1 1 A 0 C 1 E 1 C 1 A 1 R 1

Longest Common Subsequence Now, we simply fill out the chart according to the recursive rule: 1) Check to see if the "last" characters match. Recursive: If so, delete this and take the LCS of what's left and add 1 to it. Dynamic Programming: Look up&left in the table, add 1 to that. 2) If not, then we try 2 possibilities, and take the maximum of those 2 possibilities. Recursive: (These possibilities are simply taking the LCS of the whole first word and the second word minus the last letter, and vice versa. ) Dynamic Programming: Max ( cell to the left , cell above ) C R E A M R 0 1 1 A 0 1 1 2 2 C 1 1 1 2 2 E 1 1 2 2 2 C 1 1 2 2 2 A 1 1 2 3 3 R 1 2 2 3 3

Longest Common Subsequence Dynamic Programming Code… public static int compute. LCS(String a, String b) { int[][] lengths = new int[a. length()+1][b. length()+1]; // row 0 and column 0 are init. to 0 already for (int i = 1; i <= a. length(); i++) for (int j = 1; j <= b. length(); j++) if (a. char. At(i) == b. char. At(j)) lengths[i][j] = lengths[i-1][j-1] + 1; else lengths[i][j] = Math. max(lengths[i][j-1], lengths[i-1][j]); return lengths[a. length()][b. length()]; }

Edit Distance The Edit Distance (or Levenshtein distance) is a metric for measuring the amount of difference between two strings. ◦ The Edit Distance is defined as the minimum number of edits needed to transform one string into the other. It has many applications, such as spell checkers, natural language translation, and bioinformatics. ◦ An example of one application in Bioinformatics is measuring the difference between two DNA sequences.

Edit Distance The problem of finding an edit distance between two strings is as follows: ◦ Given an initial string s, and a target string t, what is the minimum number of changes that have to be applied to s to turn it into t ? The list of valid changes are: 1)Inserting a character 2)Deleting a character 3)Changing a character to another character.

Edit Distance You may think there are too many recursive cases. We could insert a character in quite a few locations! ◦ (If the string is length n, then we can insert a character in n+1 locations. ) ◦ However, the key observation that leads to a recursive solution to the problem is that ultimately, the last characters will have to match.

Edit Distance So, when matching one word to another one, consider the last characters of strings s and t. If we are lucky enough that they ALREADY match, ◦ then we can simply "cancel" and recursively find the edit distance between the two strings left when we delete this last character from both strings. Otherwise, we MUST make one of three changes: 1)delete the last character of string s 2)delete the last character of string t 3)change the last character of string s to the last character of string t. ◦ Also, in our recursive solution, we must note that the edit distance between the empty string and another string is the length of the second string. (This corresponds to having to insert each letter for the transformation. )

Edit Distance So, an outline of our recursive solution is as follows: 1) If either string is empty, return the length of the other string. 2) If the last characters of both strings match, recursively find the edit distance between each of the strings without that last character. 3) If they don't match then return 1 + minimum value of the following three choices: a) b) c) Recursive call with the string s w/o its last character and the string t Recursive call with the string s and the string t w/o its last character Recursive call with the string s w/o its last character and the string t w/o its last character.

Edit Distance Now, how do we use this to create a DP solution? ◦ We simply need to store the answers to all the possible recursive calls. ◦ In particular, all the possible recursive calls we are interested in are determining the edit distance between prefixes of s and t.

Edit Distance Consider the following example with s="hello" and t="keep". ◦ To deal with empty strings, an extra row and column have been added to the chart below: k e e p 0 1 2 3 4 h 1 1 2 3 4 e 2 2 1 2 3 l 3 3 2 2 3 l 4 4 3 3 3 o 5 5 4 4 4 An entry in this table simply holds the edit distance between two prefixes of the two strings. ◦ For example, the highlighted square indicates that the edit distance between the strings "he" and

Edit Distance In order to fill in all the values in this table we will do the following: 1) Initialize values corresponding to the base case in the recursive solution. k e e p 0 1 2 3 4 h 1 e 2 l 3 l 4 o 5

Edit Distance In order to fill in all the values in this table we will do the following: 2) Loop through the table from the top left to the bottom right. In doing so, simply follow the recursive solution. If the characters you are looking at match, Just bring down k e e p 0 1 2 3 4 h 1 1 2 e 2 2 l 3 3 l 4 4 o 5 5 the up&left value. Else the characters don't match, min ( 1+ above, 1+ left, 1+diag up) k e e p 0 1 2 3 4 h 1 1 2 e 2 2 1 l 3 3 l 4 4 o 5 5

References Slides adapted from Arup Guha’s Computer Science II Lecture notes: http: //www. cs. ucf. edu/~dmarino/ucf/cop 350 3/lectures/ Additional material from the textbook: Data Structures and Algorithm Analysis in Java (Second Edition) by Mark Allen Weiss Additional images: www. wikipedia. com xkcd. com