Algorithm Design Techniques Divide and Conquer Introduction Divide

Algorithm Design Techniques: Divide and Conquer

Introduction • Divide and conquer – algorithm makes at least two recursive calls • Subproblems should not be overlapping – Example: Fibonacci numbers • Examples – Recursive maximum subsequence sum – Linear time tree traversal – Mergesort, quicksort

Running Time • Mergesort – T(N) = 2 T(N/2) + O(N) • Theorem: The solution to the equation T(N) = a. T(N/b) + θ(Nk) where a>=1 and b>1, is T(N) = O(Nlog ba) a > bk = O(Nklog. N) a = bk = O(Nk) a < bk

Running Time: Proof • Let – N=bm N/b=bm-1 Nk=(bm)k=bmk=bkm=(bk)m • T(1) = 1 • T(bm) = a. T(bm-1)+(bk)m - divide by a m k/a)i • T(bm)/am = Σ(b i=0 • multiply by am m and use telescoping

Running Time: Proof m • T(bm) = ami=0 Σ(bk/a)i • a > bk – series will converge to a constant – T(N) = O(am) = O(alog b. N) = O(Nlog ba) • a = bk – each term in sum is 1, sum contains 1+logb. N terms, logba = k – T(N) = O(amlogb. N) = O(Nlog balogb. N) = O(Nklog. N) • a < bk – each term will be greater than 1 – T(N) = am(((bk/a)m+1 -1)/((bk/a)-1)) = O(am(bk/a)m) = O((bk)m) = O(Nk)

Running Time • Theorem: If a 1+ a 2+. . . + ak < 1, then the solution to the equation T(N) = T(a 1 N) + T(a 2 N) +. . . + T(ak. N) +O(N) is T(N) = O(N) • Idea: problem is made smaller at every step

Closest-Points Problem • p 1 = (x 1, y 1) p 2 = (x 2, y 2) • Euclidean distance between p 1 and p 2 is [(x 1 -x 2)2 + (y 1 -y 2)2]1/2 • Goal: Given N points, find closest pair • Brute force algorithm?

Closest-Points Example

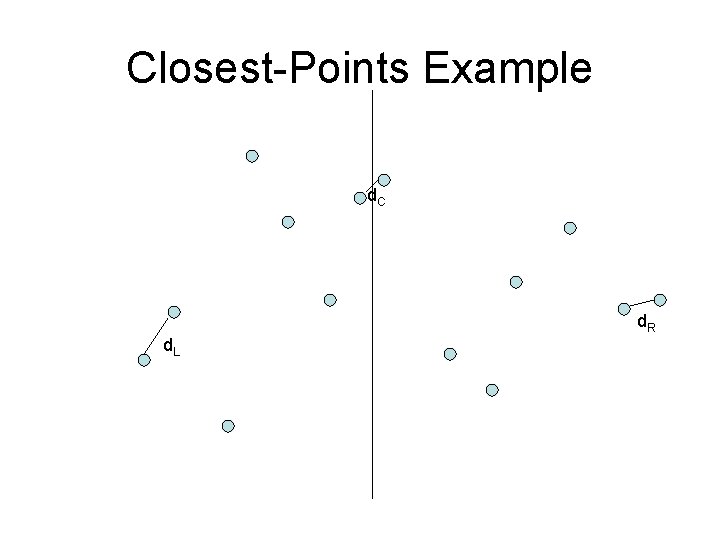
Closest-Points Problem • Brute force algorithm? – O(N 2) • Divide and Conquer – similar to maximum subsequence sum sort by X coordinate find closest two in left half (d. L) find closest two in right half (d. R) find closest two where 1 is in left, 1 in right (d. C) closest is minimum

Closest-Points Example d. C d. R d. L

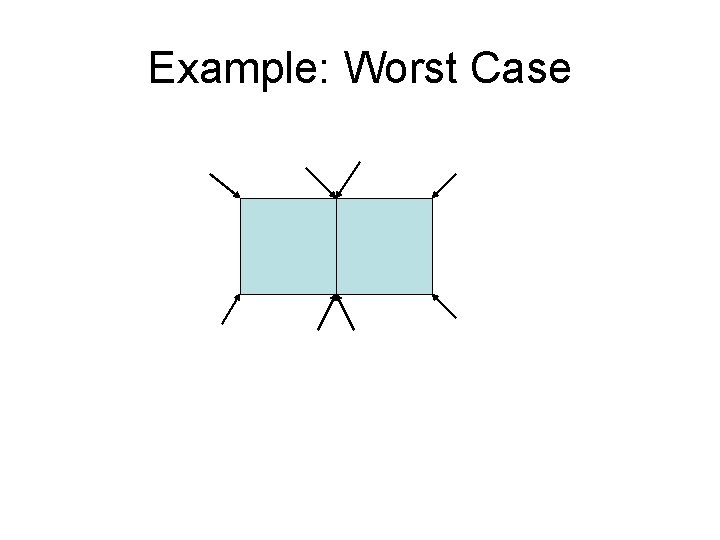
Closest-Points Problem find closest two where 1 is in left, 1 in right (d. C) • To ensure O(Nlog. N) solution, this step must be done in O(N) time – d = min(d. L, d. R) – Only need to look at points d from center – Still cannot do brute force on these points – what would be running time? – Observe: for each point, only need to consider points that are less than d away in y coordinate – There a maximum of 7 points to consider • Points must be separated by at least d • Don't need to look at points that have already been processed

Example: Worst Case

Algorithm: find. Closest T(N) = Nlog. N + 2 T(N/2) + 7 N (inner loop runs max 7 times) preprocessing step 1: sort by x coordinate preprocessing step 1: sort by y coordinate find. Closest(left) find. Closest(right) for(i=0; i<num. Points. In. Strip; i++) for(j=i+1; j<num. Points. In. Strip; j++) if(y coordinates of pi and pj differ by more than d) break; else if(dist(pi, pj) < d) d = dist(pi, pj)

Selection Problem • Find kth smallest element in a collection of N elements • Obvious algorithm? – Sort, find kth – running time? • Can be solved in O(N)

Selection Problem • Quickselect – partition (as in quicksort) into S 1 and S 2 • if k < size of S 1 – quickselect on S 1 • else if k == size of S 1 + 1 – found • else quickselect on S 2 • Running time could still be N 2 unless pivot is guaranteed to be chosen wisely

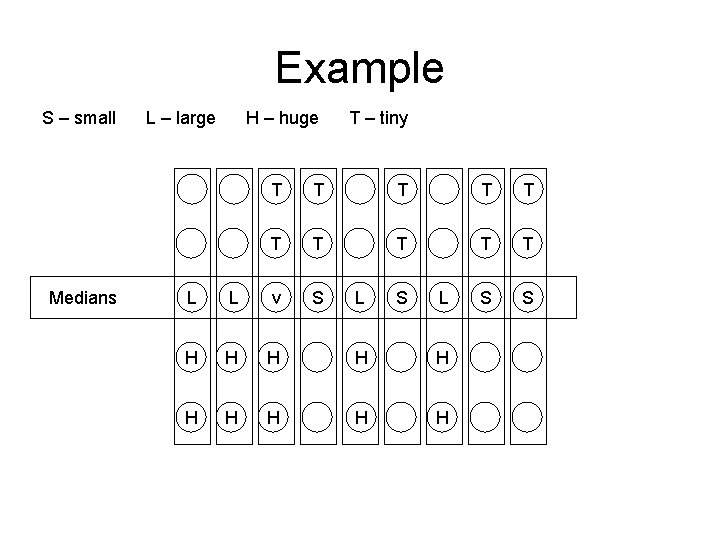
Selection Problem • Choosing the pivot – Arrange N elements into floor(N/5) groups of 5 elements – Find median of each group. This gives a list M of floor(N/5) medians. • Sort each set (8 operations) – Find median of M. Choose as pivot • Call quickselect(M/2) on M elements

Example S – small Medians L – large H – huge T – tiny T T T T T S S S L L v L S L H H H H H

Pivot Selection • • 10 k+5 = N 2 k+1 medians 1 pivot, k L's, and K S's 2 k+2 H's, and 2 k+2 T's 3 k+2 larger than pivot 3 k+2 smaller than pivot (10 k+5)-(3 k+2)-1(pivot) = max 7 k+2 in partition <. 7 N

Running Time: Quickselect • partition into N/5 arrays of size 5 and sort • find median of medians (quickselect) – use as pivot • partition • if pivot is kth element – return • else quickselect on appropriate partition T(N) = 8(N/5) + T(. 2 N) + N + T(. 7 N) = O(N)

Multiplying Integers • • x = 61, 438, 521 y = 94, 736, 407 Typical algorithm is N 2 Use divide and conquer! XL=6, 143 XR=8, 521 YL=9, 473 YR=6, 407 X = XL 104+XR Y = YL 104+YR XY = XLYL 108 + (XLYR + XRYL)104 + XRYR T(N) = 4 T(N/2) + O(N) = O(N 2)

Multiplying Integers • XY = XLYL 108 + (XLYR + XRYL)104 + XRYR • X LY R + X RY L = (XL – XR)(YR-YL)+XLYL+XRYR • Use 1 multiplication plus 2 results already computed • T(N) = 3 T(N/2) + O(N) • T(N) = O(Nlog 23) = O(N 1. 59)

Matrix Multiplication A=3416 1257 5129 4356 B=5693 4531 1184 3141 Ci, j = dot product of ith row of A and jth col of B C 0, 0 = (3*5)+(4*4)+(1*1)+(6*3) Brute force algorithm = O(N 3)

Matrix Multiplication A 1, 1 A 1, 2 A 2, 1 A 2, 2 B 1, 1 B 1, 2 B 2, 1 B 2, 2 = C 1, 1 = A 1, 1 B 1, 1 + A 1, 2 B 2, 1 C 1, 2 = A 1, 1 B 1, 2 + A 1, 2 B 2, 2 C 2, 1 = A 2, 1 B 1, 1 + A 2, 2 B 2, 1 C 2, 2 = A 2, 1 B 1, 2 + A 2, 2 B 2, 2 C 1, 1 C 1, 2 C 2, 1 C 2, 2

Matrix Multiplication • T(N) = 8 T(N/2) + O(N 2) – additions take N 2 • Still O(N 3) M 1 = (A 1, 2 - A 2, 2) (B 2, 1+ B 2, 2) M 2 = (A 1, 1+A 2, 2) (B 1, 1+ B 2, 2) M 3 = (A 1, 1 - A 2, 1) (B 1, 1+ B 1, 2) M 4 = (A 1, 1+ A 1, 2) (B 2, 2) M 5 = (A 1, 1) (B 1, 2 -B 2, 2) M 6 = (A 2, 2) (B 2, 1 -B 1, 1) M 7 = (A 2, 1+ A 2, 2) (B 1, 1)

Matrix Multiplication C 1, 1 = M 1 + M 2 – M 4 + M 6 C 1, 2 = M 4 + M 5 C 2, 1 = M 6 + M 7 C 2, 2 = M 2 - M 3 + M 5 - M 7 T(N) = 7 T(N/2) + O(N 2) = O(Nlog 27) = O(N 2. 81)