Lecture 6 More DivideConquer and Paradigm 4 Data

Lecture 6 More Divide-Conquer and Paradigm #4 Data Structure. n Today, we do more “divide-and-conquer”. n And, we do Algorithm design paradigm # 4: invent or augment a data structure.

More divide and conquer: powering a number n Problem: Compute an , where n is an integer. n Naïve algorithm Θ(n). n Divide-and-conquer: an = an/2 = a(n-1)/2 a if n is even. if n is odd Note, another kind of divide and conquer. Time complexity: T(n) = T(n/2) + Θ(1) = Θ(logn)

Back to Fibonacci numbers n Recursion: not careful would give exponential time algorithm. n Plain linear bottom up computation: Θ(n). n Can we do better? n Theorem: Fn+1 Fn 1 1 Fn Fn-1 1 0 I will prove this in class. Then you can compute this similar to powering of an integer in Θ(logn) steps.

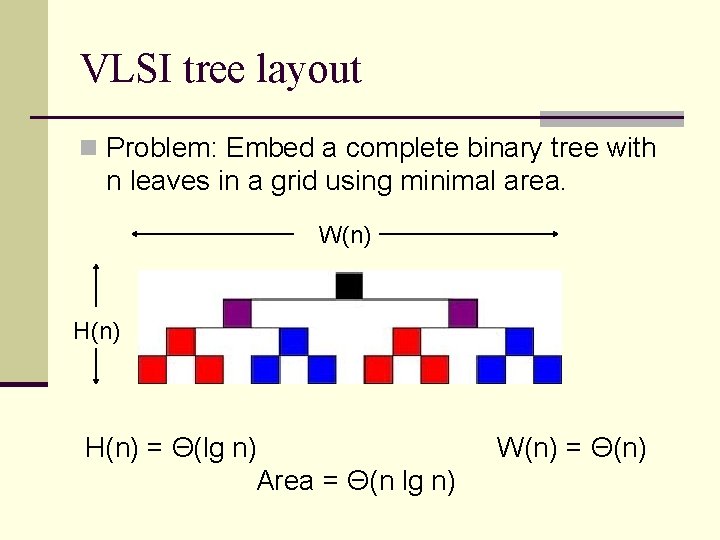
VLSI tree layout n Problem: Embed a complete binary tree with n leaves in a grid using minimal area. W(n) H(n) = Θ(lg n) Area = Θ(n lg n) W(n) = Θ(n)

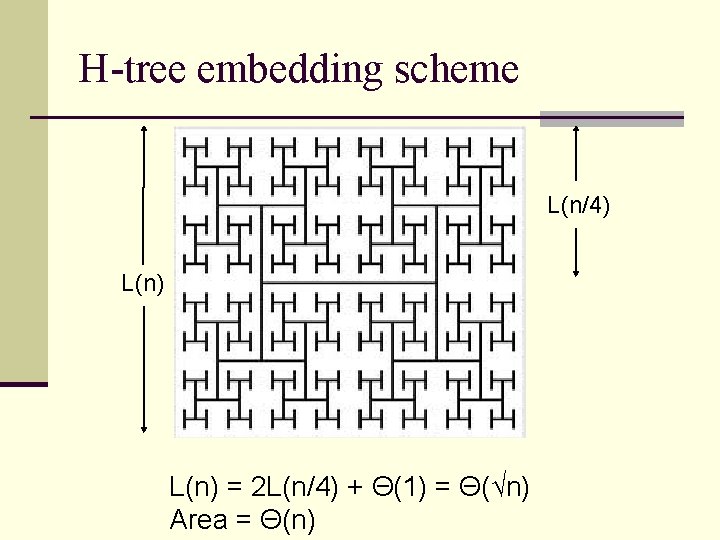
How do we improve this embedding? n If we wish to have an O(n) solution for the area, perhaps we wish to have √n for L(n) and W(n). n What recursion scheme would get us there? n The Master theorem Case 1 says if b=4, a=2, then log 4 2 =1/2. So if we have something like T(n) = 2 T(n/4) + o(√n) we would get O(√n) solution for L(n) and W(n).

H-tree embedding scheme L(n/4) L(n) = 2 L(n/4) + Θ(1) = Θ(√n) Area = Θ(n)

Paradigm #4 Use a data structure.

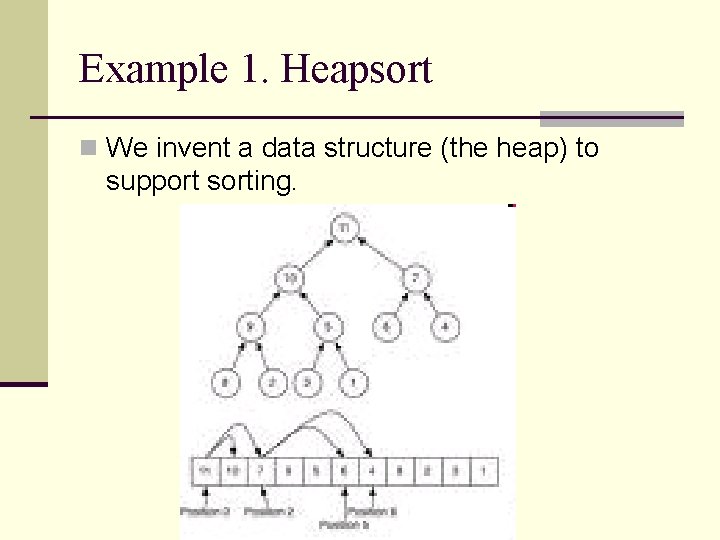
Example 1. Heapsort n We invent a data structure (the heap) to support sorting.

Example 2. Subrange sum n We want to maintain an array of integers a[1. . n], and support the following operations: A. Increment a[i] by b; that is, set a[i] += b. n B. Subrange sum: compute the sum of the elements a[c], a[c+1], . . . , a[d]. n n Augment array as follows: a[1] a[2] a[3] a[4] a[5] a[6] a[7] a[8] a[1. . 2] a[3. . 4] a[5. . 6] a[7. . 8] a[1. . 4] a[5. . 8] a[1. . 8] n Operations A and B are both in O(logn) time.