CS 552 Computer Graphics Lecture 33 Illumination and

CS 552: Computer Graphics Lecture 33: Illumination and Shading

Recap • Solid Modeling o Represent the solid object in a 3 D space o B-Reps o Subdividing algorithms

Objective • After completing this lecture, students will be able to o Explain the importance of VSDs o Solve the problem of backface culling

Surface Rendering Method • Realistic displays of a scene are obtained by o Generating perspective projections of objects and o Applying natural lighting effects to the visible surfaces • An illumination model is used to calculate the color of an illuminated position on the surface of an object. • A surface-rendering method uses the color calculations from an illumination model to determine the pixel colors for all projected positions in a scene.

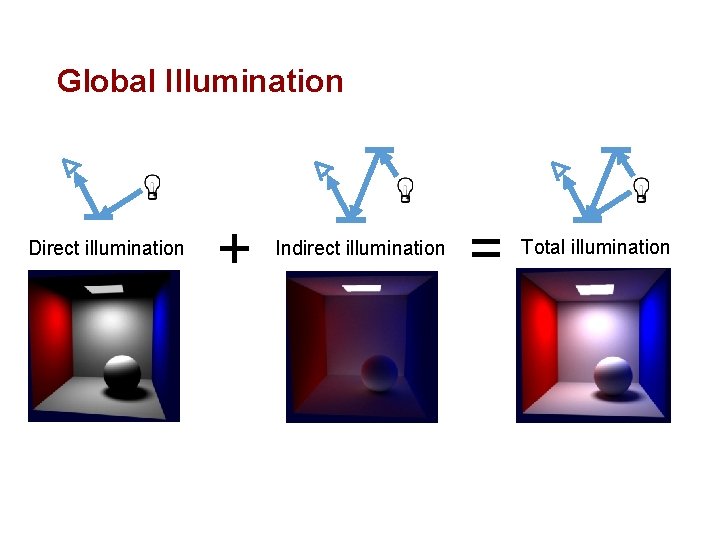
Global Illumination Direct illumination + Indirect illumination = Total illumination

Diffuse Inter-reflection Total illumination (normal image)

Diffuse Inter-reflection Direct illumination

Diffuse Interreflection Indirect illumination (diffuse interreflection)

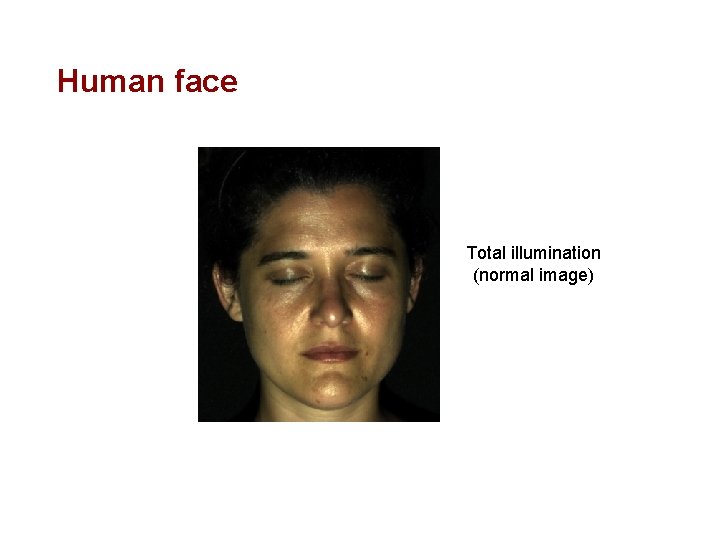
Human face Total illumination (normal image)

Human face Direct illumination

Human face Indirect illumination

Illumination • How do We Compute Radiance for a Sample Ray? o Must derive computer models for. . . ØEmission at light sources ØScattering at surfaces ØReception at the camera Wireframe Without Illumination Direct Illumination

Overview • Direct Illumination o Emission at light sources o Scattering at surfaces • Global Illumination o Shadows o Refractions o Inter-object reflections Direct Illumination

Overview • Direct Illumination o Emission at light sources o Scattering at surfaces • Global Illumination o Shadows o Refractions o Inter-object reflections Direct Illumination

Modeling Light Source • IL(x, y, z, q, f, l) o Describes the intensity of energy, o Leaving a light source o Arriving at location(x, y, z) o From direction (q, f) o With wavelength l

Empirical Model • Ideally Measure Irradiant Energy for “All” Situations o Too much storage o Difficult in practice

Light Source Model • Simple Mathematical Models: o Point light o Directional light o Spot light

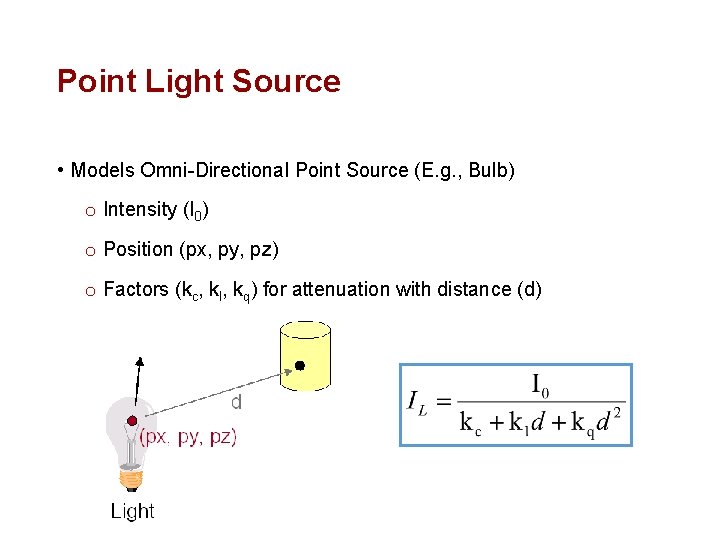
Point Light Source • Models Omni-Directional Point Source (E. g. , Bulb) o Intensity (I 0) o Position (px, py, pz) o Factors (kc, kl, kq) for attenuation with distance (d)

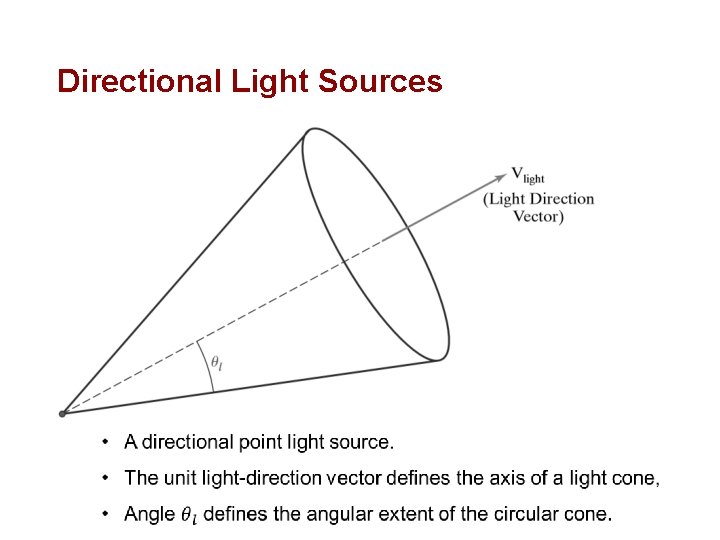
Directional Light Source • Models Point Light Source at Infinity (E. g. , Sun) o Intensity (I 0) o Direction (dx, dy, dz) No attenuation with distance

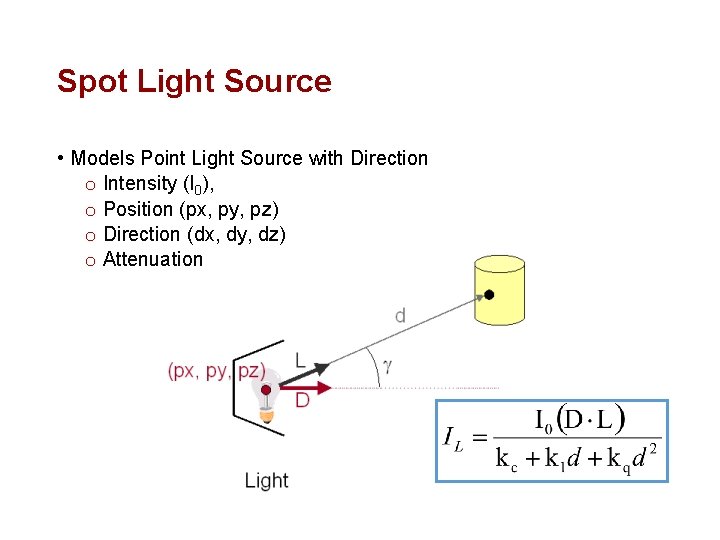
Spot Light Source • Models Point Light Source with Direction o Intensity (I 0), o Position (px, py, pz) o Direction (dx, dy, dz) o Attenuation

Directional Light Sources

Angular Intensity Attenuation • Attenuate the light intensity o Angularly about the source o Radially out from the point-source position.

Overview • Direct Illumination o Emission at light sources o Scattering at surfaces • Global Illumination o Shadows o Refractions o Inter-object reflections Direct Illumination

Modeling Surface Reflection • Rs(q, f, g, y, l) o Describes the amount of incident energy o Arriving from direction (q, f) o Leaving in direction (g, y) o With wavelength l

Empirical Model • Ideally Measure Radiant Energy for “All” Combinations of Incident Angles o Too much storage o Difficult in practice

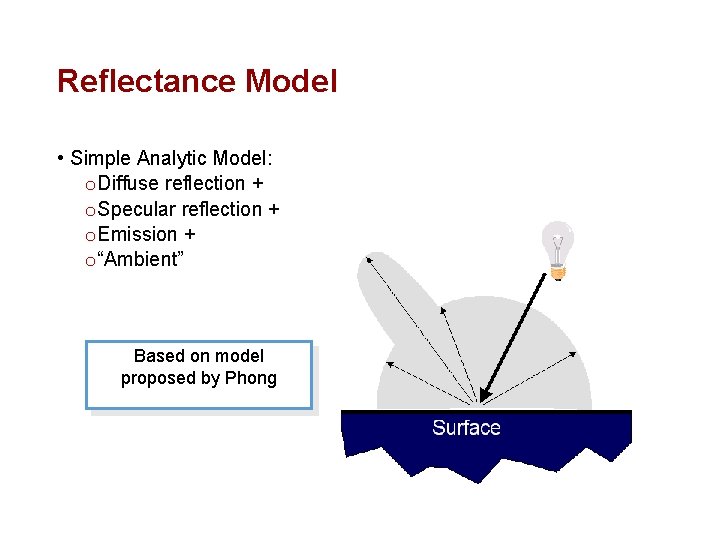
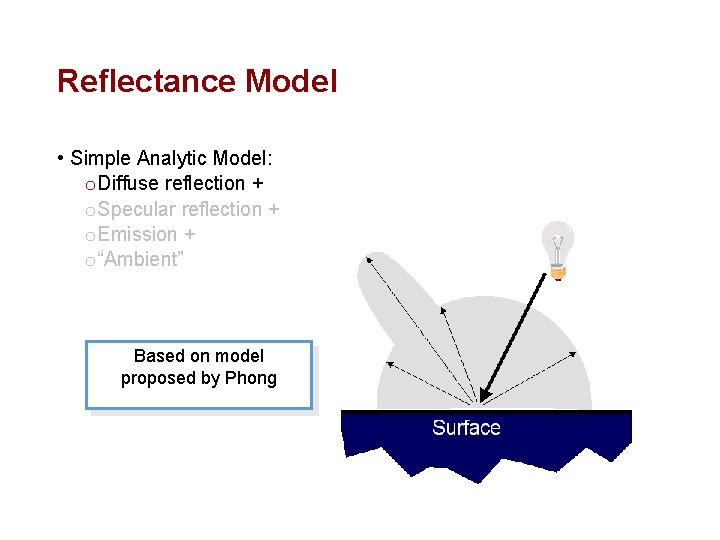
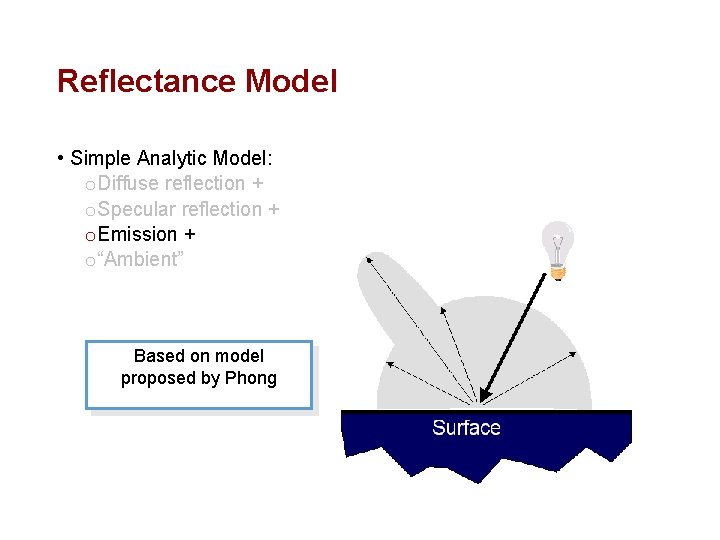
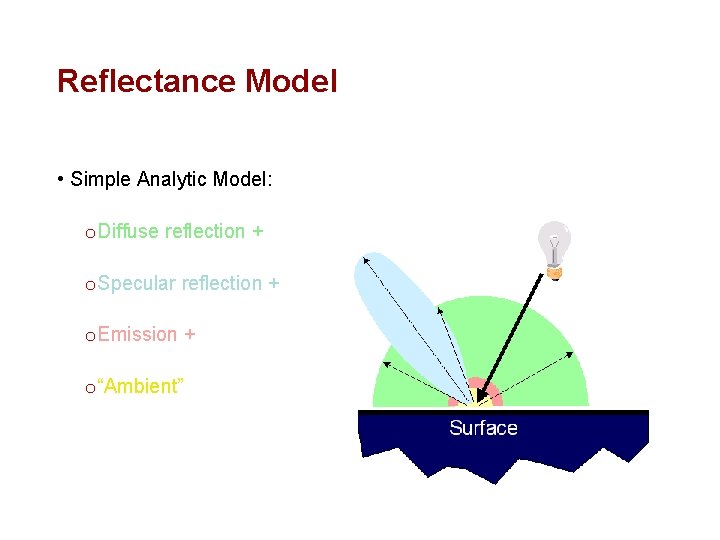
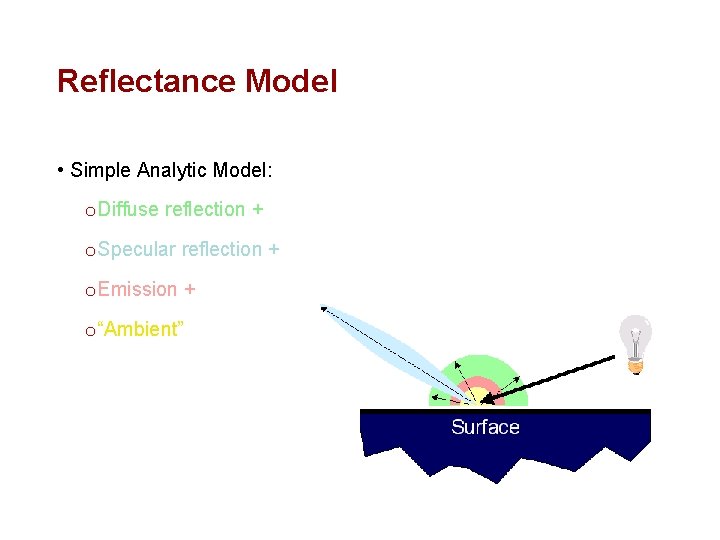
Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient” Based on model proposed by Phong

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient” Based on model proposed by Phong

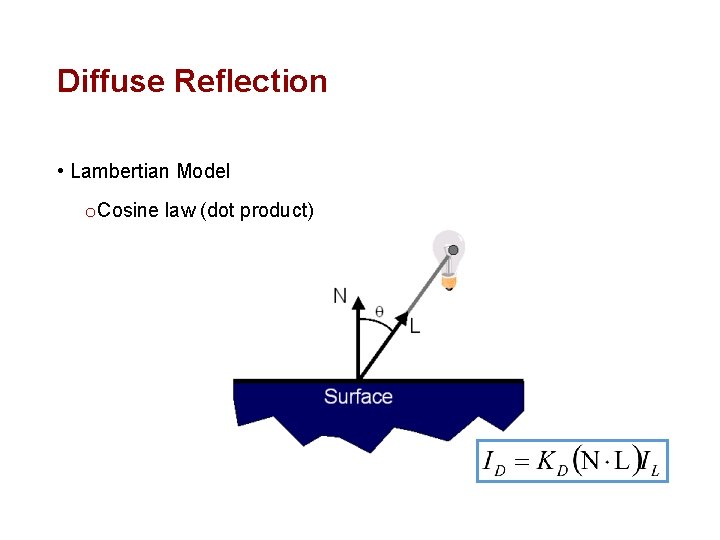
Diffuse Reflection • Assume Surface Reflects Equally in All Directions o Examples: chalk, clay

Diffuse Reflection • How Much Light is Reflected? o Depends on angle of incident light o d. L = d. A cos Q

Diffuse Reflection • Lambertian Model o Cosine law (dot product)

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient” Based on model proposed by Phong

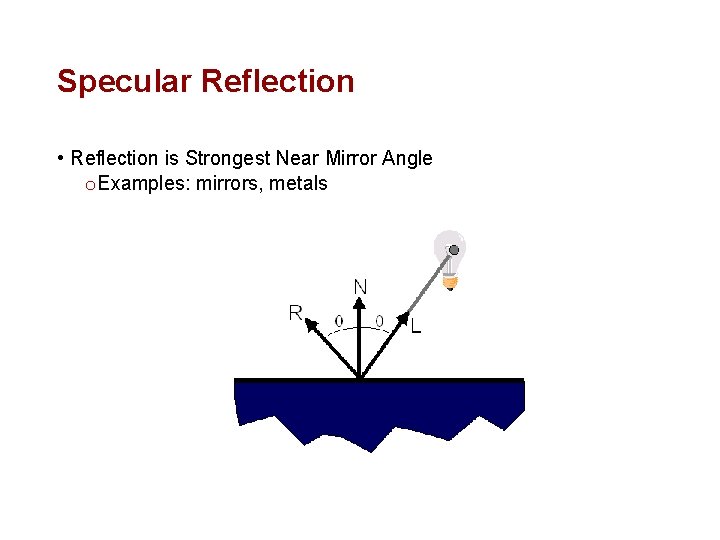
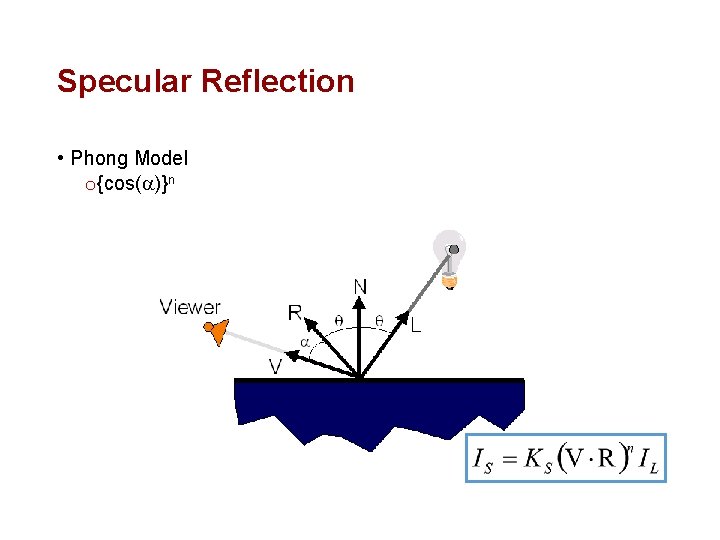
Specular Reflection • Reflection is Strongest Near Mirror Angle o Examples: mirrors, metals

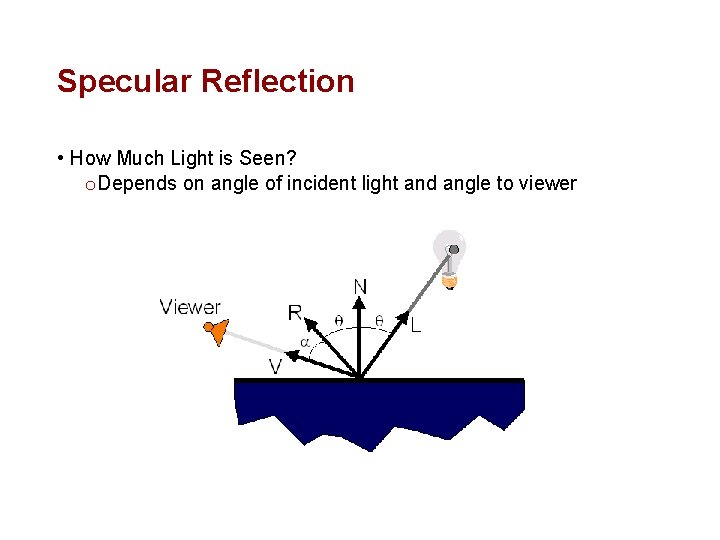
Specular Reflection • How Much Light is Seen? o Depends on angle of incident light and angle to viewer

Specular Reflection • Phong Model o {cos(a)}n

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient” Based on model proposed by Phong

Emission • Represents Light Emitting Directly From Polygon Emission ≠ 0

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient” Based on model proposed by Phong

Ambient Term • Represents Reflection of All Indirect Illumination

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient”

Reflectance Model • Simple Analytic Model: o Diffuse reflection + o Specular reflection + o Emission + o “Ambient”

Reflectance Model • Sum Diffuse, Specular, Emission, and Ambient

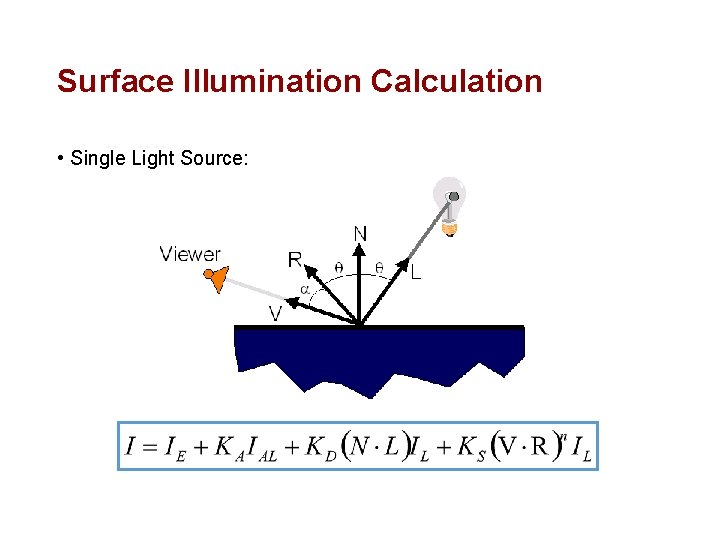
Surface Illumination Calculation • Single Light Source:

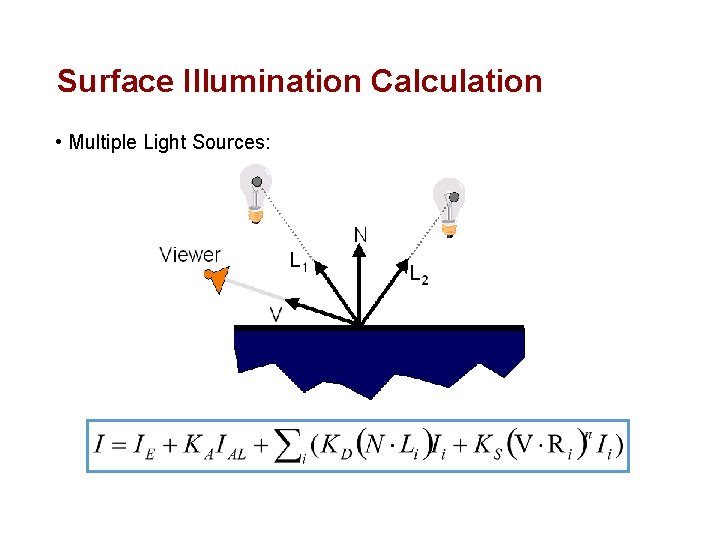
Surface Illumination Calculation • Multiple Light Sources:

Overview • Direct Illumination o Emission at light sources o Scattering at surfaces • Global Illumination o Shadows o Refractions o Inter-object reflections Global Illumination

Global Illumination

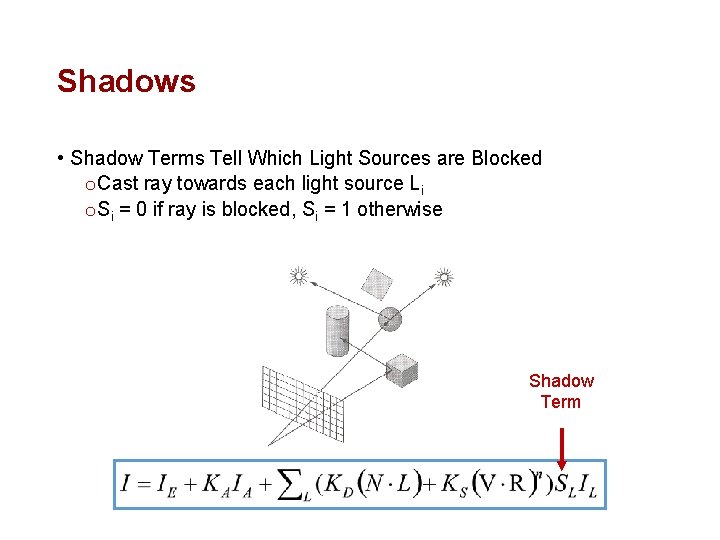
Shadows • Shadow Terms Tell Which Light Sources are Blocked o Cast ray towards each light source Li o Si = 0 if ray is blocked, Si = 1 otherwise Shadow Term

Ray Casting • Trace Primary Rays from Camera o Direct illumination from unblocked lights only

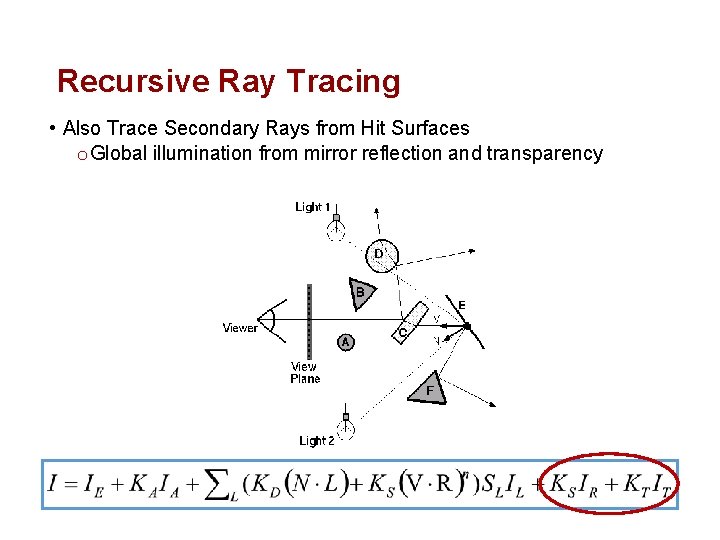
Recursive Ray Tracing • Also Trace Secondary Rays from Hit Surfaces o Global illumination from mirror reflection and transparency

Mirror Reflection • Trace Secondary Ray in Direction of Mirror Reflection o Evaluate radiance along secondary ray and include it into illumination model Radiance for mirror reflection ray

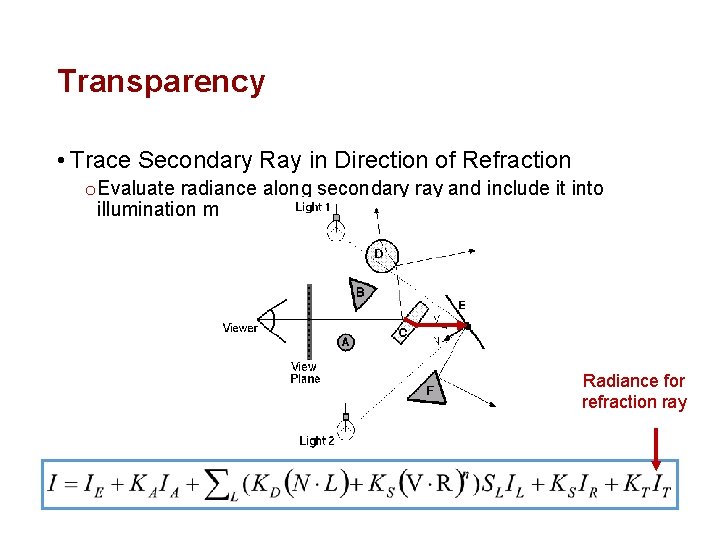
Transparency • Trace Secondary Ray in Direction of Refraction o Evaluate radiance along secondary ray and include it into illumination model Radiance for refraction ray

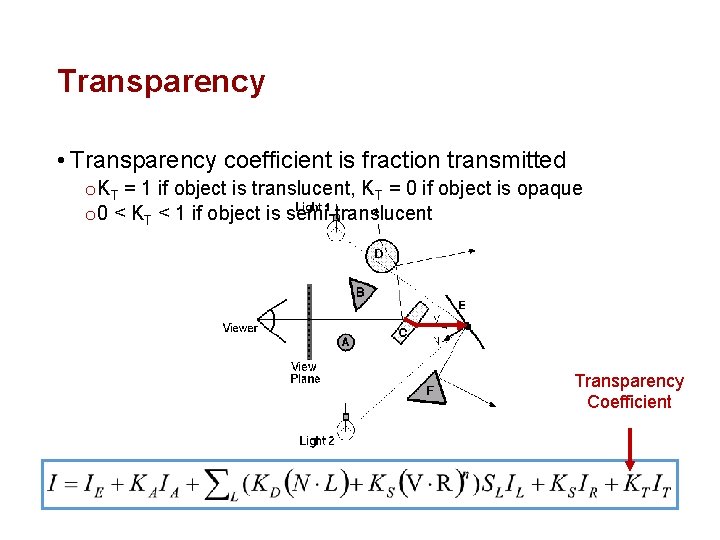
Transparency • Transparency coefficient is fraction transmitted o KT = 1 if object is translucent, KT = 0 if object is opaque o 0 < KT < 1 if object is semi-translucent Transparency Coefficient

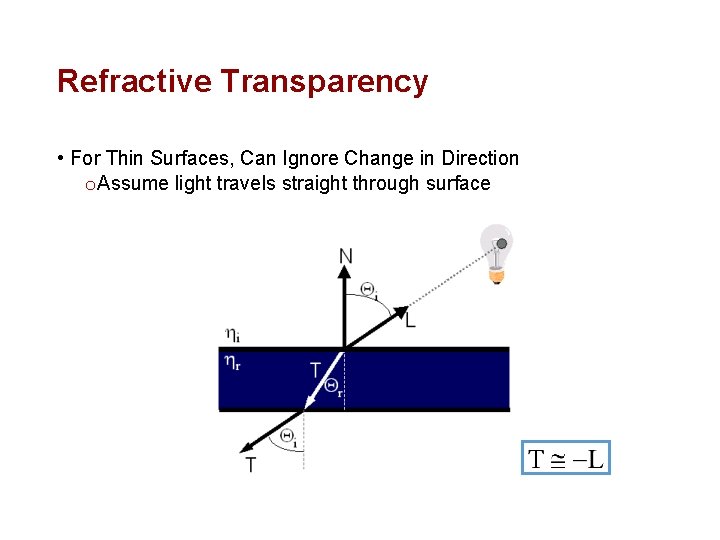
Refractive Transparency • For Thin Surfaces, Can Ignore Change in Direction o Assume light travels straight through surface

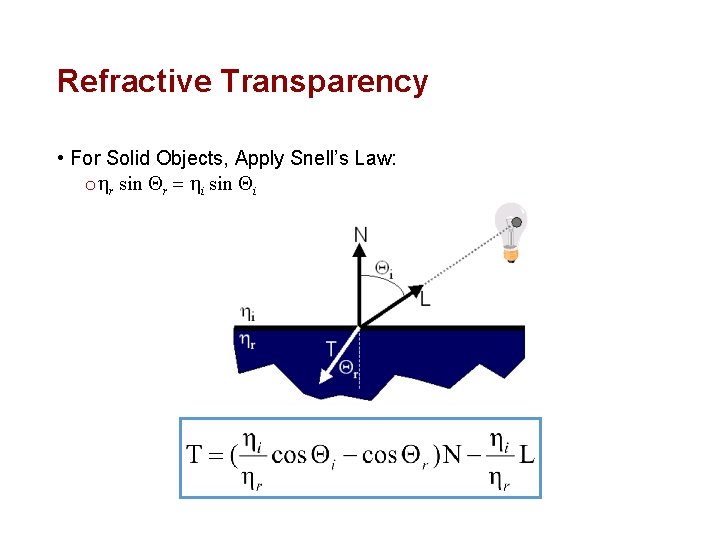
Refractive Transparency • For Solid Objects, Apply Snell’s Law: o hr sin Qr = hi sin Qi

Summary • Direct Illumination o Ray casting o Usually use simple analytic approximations for light source emission and surface reflectance • Global illumination o Recursive ray tracing o Incorporate shadows, mirror reflections, and pure refractions

Illumination Terminology • Radiant power [flux] (Φ) o Rate at which light energy is transmitted (in Watts). • Radiant Intensity (I) o Power radiated onto a unit solid angle in direction( in Watt/sr) Øe. g. : energy distribution of a light source (inverse square law) • Radiance (L) o Radiant intensity per unit projected surface area( in Watts/m 2 sr) Øe. g. : light carried by a single ray (no inverse square law) • Irradianc (E) o Incident flux density on a locally planar area (in Watts/m 2 ) • Radiosity (B) o Exitant flux density from a locally planar area ( in Watts/m 2 )

Thank you Next Lecture: Rendering