Continuidade de fx 1 Intuitivo funo contnua O

Continuidade de f(x) 1

Intuitivo – função contínua O gráfico pode ser desenhado sem levantar o lápis do papel. . . porque não tem interrupções. . . (é contínuo. . . ) 2

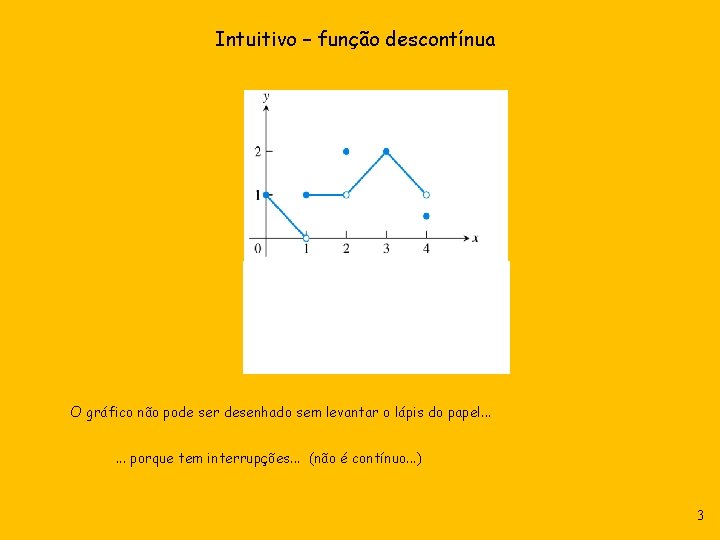
Intuitivo – função descontínua O gráfico não pode ser desenhado sem levantar o lápis do papel. . . porque tem interrupções. . . (não é contínuo. . . ) 3

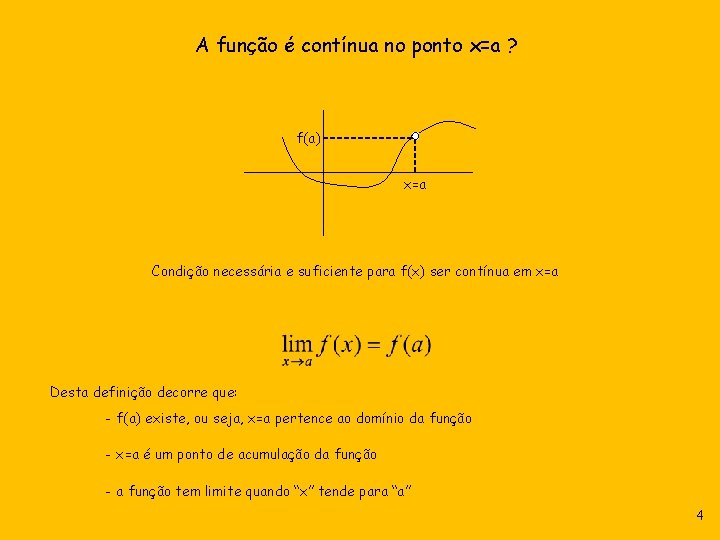
A função é contínua no ponto x=a ? f(a) x=a Condição necessária e suficiente para f(x) ser contínua em x=a Desta definição decorre que: - f(a) existe, ou seja, x=a pertence ao domínio da função - x=a é um ponto de acumulação da função - a função tem limite quando “x” tende para “a” 4

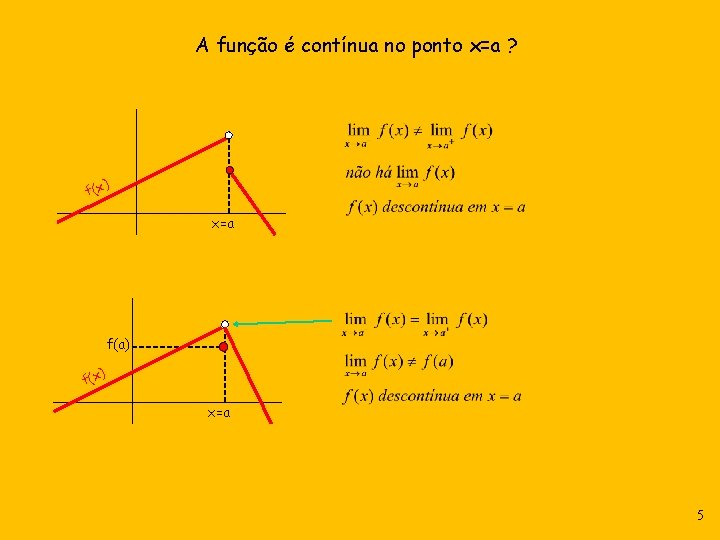
A função é contínua no ponto x=a ? ) f(x x=a f(a) ) f(x x=a 5

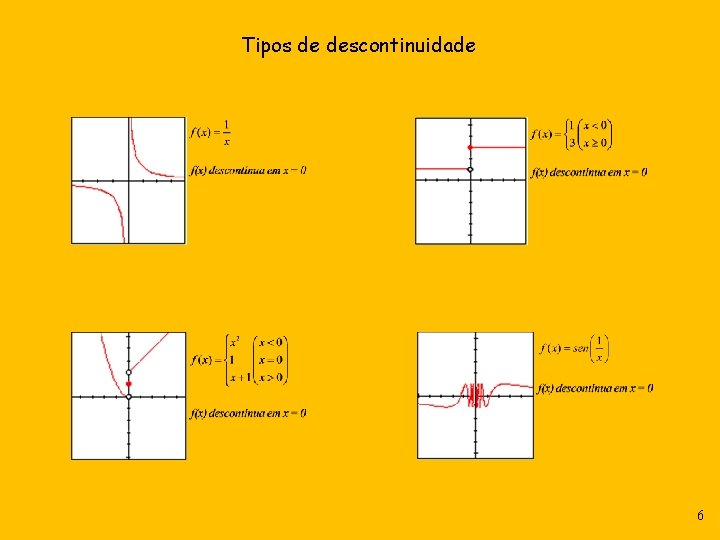
Tipos de descontinuidade 6

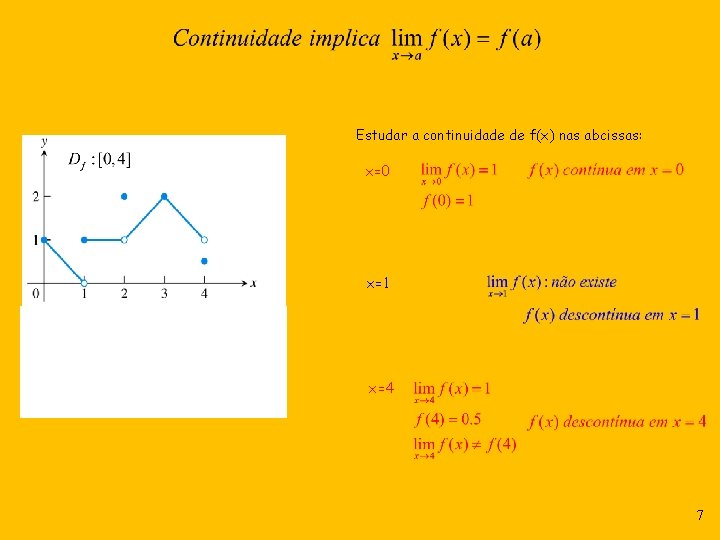
Estudar a continuidade de f(x) nas abcissas: x=0 x=1 x=4 7

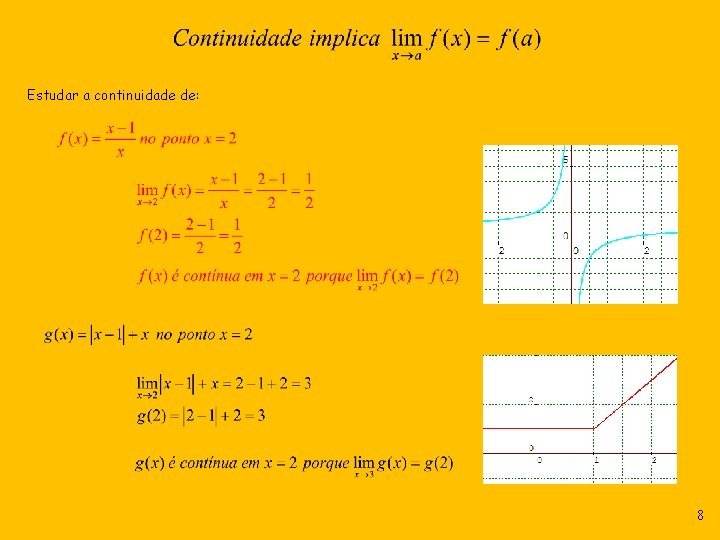
Estudar a continuidade de: 8

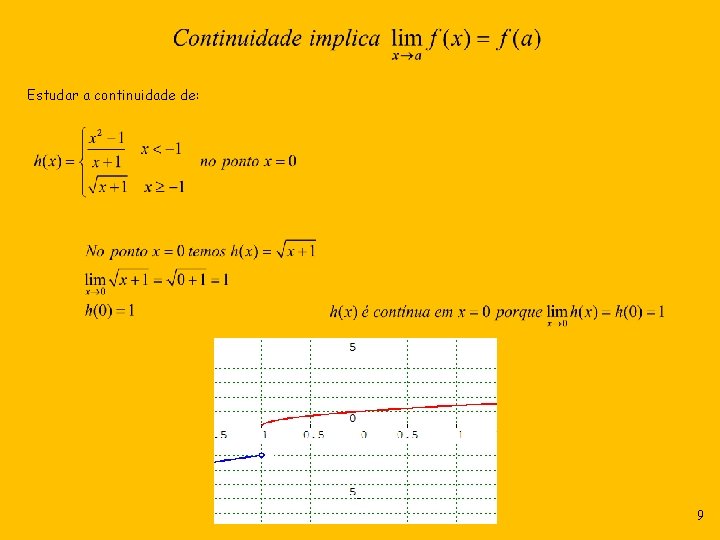
Estudar a continuidade de: 9

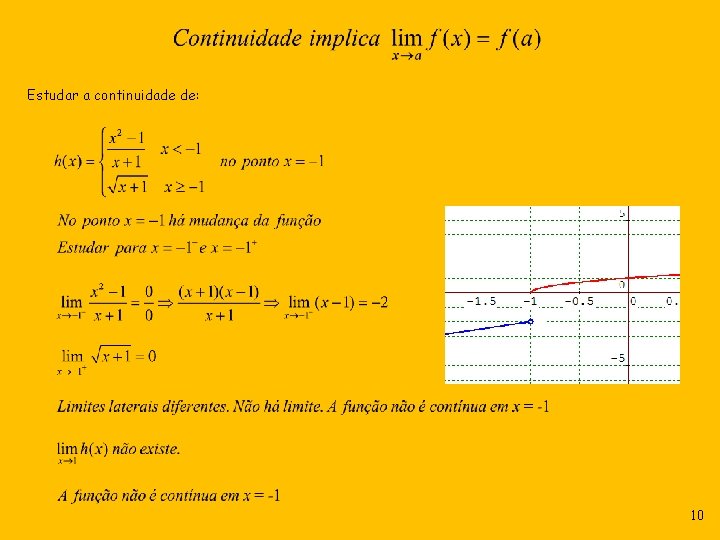
Estudar a continuidade de: 10

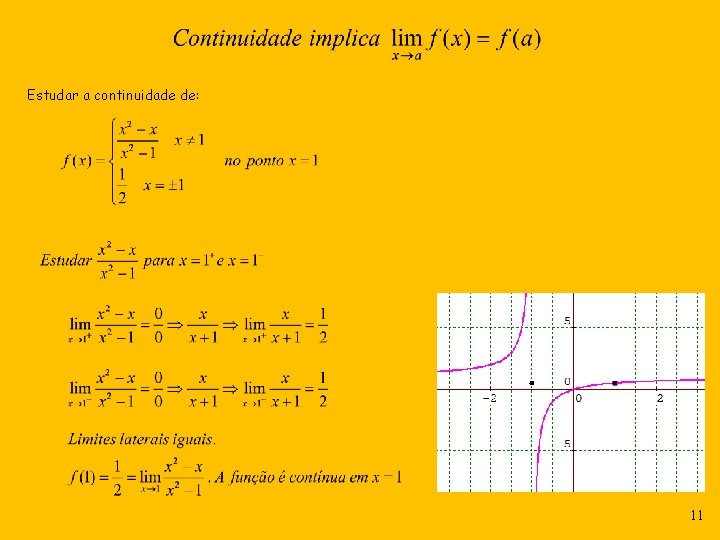
Estudar a continuidade de: 11

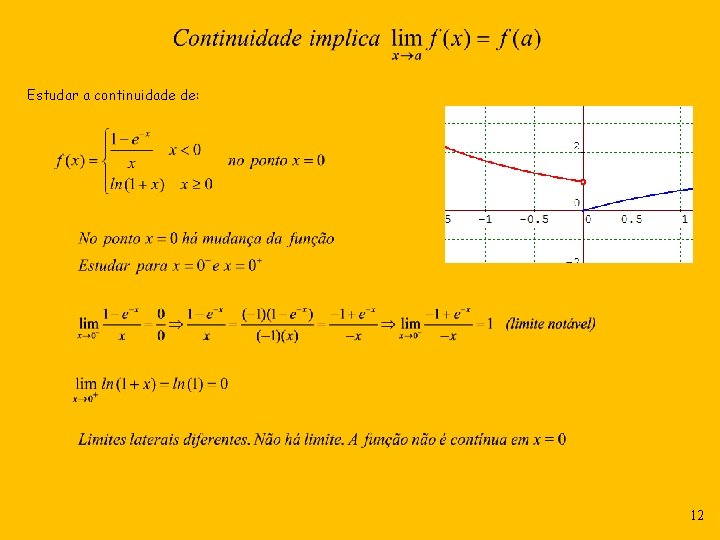
Estudar a continuidade de: 12

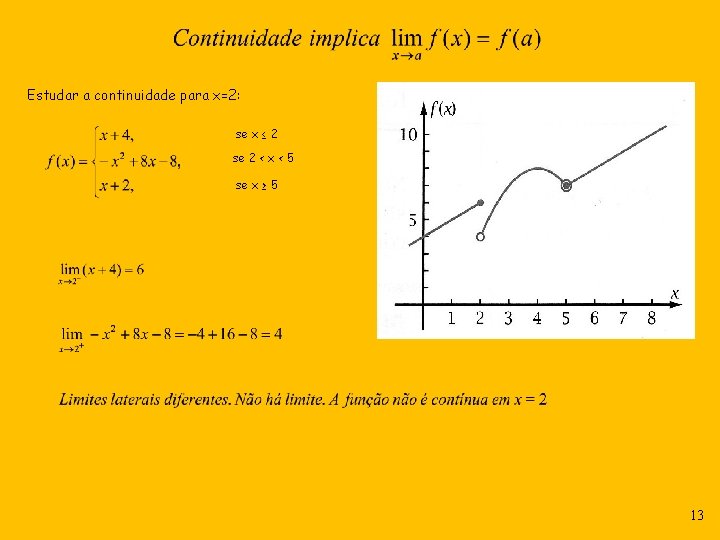
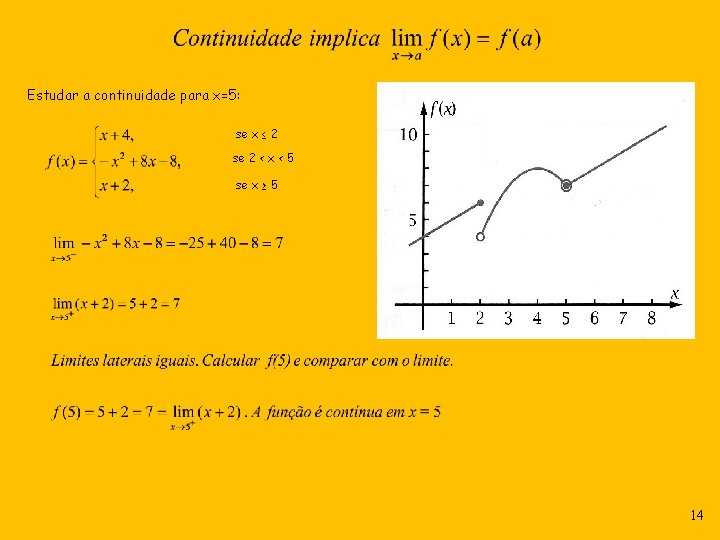
Estudar a continuidade para x=2: se x ≤ 2 se 2 < x < 5 se x ≥ 5 13

Estudar a continuidade para x=5: se x ≤ 2 se 2 < x < 5 se x ≥ 5 14

Continuidade Funções polinomiais Funções exponenciais são contínuas em R Funções logarítmicas Funções racionais Funções irracionais são contínuas no seu domínio 15

Continuidade - Operações Se f(x) e g(x) são contínuas no ponto x=a então são contínuas no mesmo ponto: A sua soma f+g A sua diferença f-g O seu produto fxg O seu quociente f/g (sendo g ≠ 0) A função composta fo g Se f(x) é contínua no ponto x=a então também é contínua: 16

Onde são contínuas as funções a seguir indicadas? 17

Indicar os valores de “x” para os quais as funções são contínuas 18

Função Contínua num intervalo f(x) é contínua no intervalo ABERTO ]a, b[ do seu domínio se é contínua em todos os pontos do intervalo f(x) é contínua no intervalo FECHADO [a, b] do seu domínio se é contínua no intervalo ABERTO ]a, b[ e também contínua se “x” tende para a+ e para b- f(x) é contínua no intervalo [1, 4[ ? f(x) com domínio [-1, 4] 19

Função Contínua num intervalo f(x) é contínua no intervalo ABERTO ]a, b[ do seu domínio se é contínua em todos os pontos do intervalo f(x) é contínua no intervalo FECHADO [a, b] do seu domínio se é contínua no intervalo ABERTO ]a, b[ e também contínua se “x” tende para a+ e para b- f(x) é contínua no intervalo [1, 4] ? f(x) com domínio [-1, 4] 20

Função Contínua num intervalo f(x) é contínua no intervalo ABERTO ]a, b[ do seu domínio se é contínua em todos os pontos do intervalo f(x) é contínua no intervalo FECHADO [a, b] do seu domínio se é contínua no intervalo ABERTO ]a, b[ e também contínua se “x” tende para a+ e para b- f(x) é contínua no intervalo [-1, 2] ? f(x) com domínio [-1, 4] 21

Teorema de Bolzano- Cauchy Admita-se f(x) contínua no intervalo fechado [a, b] Para qualquer valor “y 0” do intervalo [f(a), f(b)] há, pelo menos, um valor “c” do intervalo [a, b] tal que f(c) = y 0 22

Exercício Provar que existe x=c no intervalo [0, 2] sabendo que f(x) = x 2 + 2 x - 3 com f(c)=2 1º f(x) é polinomial; a função é contínua 5 2º nos extremos do intervalo os valores de f(x) são f(0) = -3 e f(2) = 5 2 -3 3º Porque o valor f(c)=2 pertence ao intervalo [f(0), f(2)] conclui-se , de acordo com o teorema Bolzano-Cauchy que a abcissa 2, pertence ao intervalo dado. c c=1. 45 23

Casos Particulares f(x) é contínua no intervalo fechado [a, b] O produto [f(a) x f(b)] é Negativo. Conclusão: no mínimo, há um zero de f (x) no intervalo [a, b] 24

Exercício f(a) e f(b)] têm sinais contrários (produto negativo). Não há nenhum zero. . . Porquê ? Porque a função não é contínua 25

Exercício Usando o teorema de Bolzano provar que a função tem pelo menos um zero no intervalo proposto 1º Estudar a continuidade de f(x) no intervalo proposto A função é contínua porque é a soma de duas funções contínuas: função logarítmica contínua neste intervalo e função polinomial contínua no campo real 2º Calcular f(x) nos extremos do intervalo e comparar os sinais Conclusão: f(x) tem pelo menos um zero porque é contínua no intervalo proposto e tem valores de sinais diferentes nos extremos do intervalo 26

Exercício A função f(x) é contínua no intervalo [0, 5] com contradomínio [-3, -1]. O domínio, da função g(x) = f(x) + x, é [0, 5]. Provar que g(x) tem, pelo menos, um zero. 1º g(x) é soma de duas funções contínuas no intervalo [0, 5] pelo que também é contínua neste intervalo 2º Calcular o valor de g(0) e g(5) Conclusão: g(x) < 0 e g(x) > 0 para x=0 e x=5 respectivamente. Conforme o teorema de Bolzano, g(x) tem pelo menos um zero neste intervalo. 27

Exercício Recorrendo ao teorema de Bolzano provar que há, pelo menos, uma solução no intervalo [2, e] 2º Calcular o valor da equação em x=2 e x=e Conclusão: f(x) < 0 e f(x) > 0 para x=2 e x=e respectivamente. Conforme o teorema de Bolzano, f(x) tem, pelo menos, a solução zero neste intervalo. 28

29