Compiler Construction Finitestate automata 1 Todays Goals n

Compiler Construction Finite-state automata 1

Today’s Goals n More on lexical analysis: cycle of construction n n RE NFA DFA → → NFA DFA Minimal DFA RE Engineering issues in building scanners 2

Overview n The cycle of construction n Direct construction of a Nondeterministic Finite Automaton (NFA) to recognize a given RE n n Construct a Deterministic Finite Automaton (DFA) to simulate the NFA n n Use a set-of-states construction Minimize the number of states in DFA n n Requires ε-transitions to combine regular subexpressions Hopcroft state minimization algorithm Derive regular expression from DFA 3

More Regular Expressions n All strings of 1 s and 0 s ending in a 1 ( 0 | 1 )* 1 n All strings over lowercase letters where the vowels (a, e, i, o, & u) occur exactly once, in ascending order Cons → (b|c|d|f|g|h|j|k|l|m|n|p|q|r|s|t|v|w|x|y|z) Cons* a Cons* e Cons* i Cons* o Cons* u Cons* n All strings of 1 s and 0 s that do not contain three 0 s in a row: 4

More Regular Expressions n All strings of 1 s and 0 s ending in a 1 ( 0 | 1 )* 1 n All strings over lowercase letters where the vowels (a, e, i, o, & u) occur exactly once, in ascending order Cons → (b|c|d|f|g|h|j|k|l|m|n|p|q|r|s|t|v|w|x|y|z) Cons* a Cons* e Cons* i Cons* o Cons* u Cons* n All strings of 1 s and 0 s that do not contain three 0 s in a row: ( 1* ( ε |01 | 001 ) 1* )* ( ε | 00 ) 5

Non-deterministic Finite Automata Each RE corresponds to a deterministic finite automaton (DFA) n May be hard to directly construct the right DFA What about an RE such as ( a | b )* abb ? This is a little different n S 0 has a transition on ε n S 1 has two transitions on a This is a non-deterministic finite automaton (NFA) 6

Non-deterministic Finite Automata n n An NFA accepts a string x iff ∃ a path through the transition graph from s 0 to a final state such that the edge labels spell x Transitions on ε consume no input To “run” the NFA, start in s 0 and guess the right transition at each step n n n Always guess correctly If some sequence of correct guesses accepts x then accept Why study NFAs? n n They are the key to automating the RE→DFA construction We can paste together NFAs with ε-transitions 7

Relationship between NFA and DFA is a special case of an NFA n n n DFA has no ε transitions DFA’s transition function is single-valued Same rules will work DFA can be simulated with an NFA n Obviously NFA can be simulated with a DFA n n n (less obvious) Simulate sets of possible states Possible exponential blowup in the state space Still, one state per character in the input stream 8

Automating Scanner Construction n To convert a specification into code: 1. 2. 3. 4. 5. n Write down the RE for the input language Build a big NFA Build the DFA that simulates the NFA Systematically shrink the DFA Turn it into code Scanner generators n n Lex and Flex work along these lines Algorithms are well-known and well-understood Key issue is interface to parser (define all parts of speech) You could build one in a weekend! 9

Automating Scanner Construction RE→ NFA (Thompson’s construction) n Build an NFA for each term n Combine them with ε-moves NFA → DFA (subset construction) n Build the simulation DFA → Minimal DFA n Hopcroft’s algorithm DFA →RE (Not part of the scanner construction) n All pairs, all paths problem n Take the union of all paths from s 0 to an accepting state 10

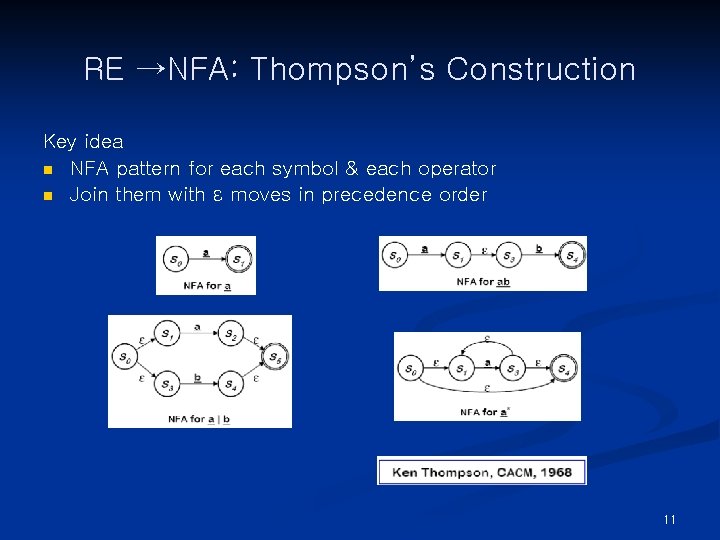
RE →NFA: Thompson’s Construction Key idea n NFA pattern for each symbol & each operator n Join them with ε moves in precedence order 11

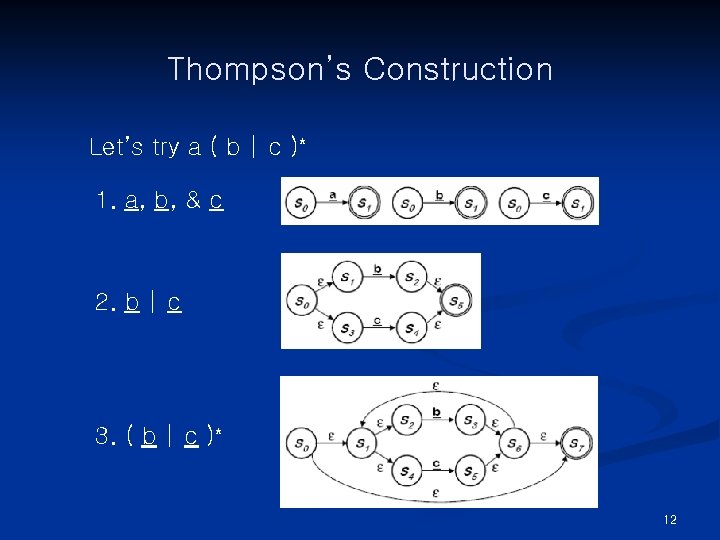
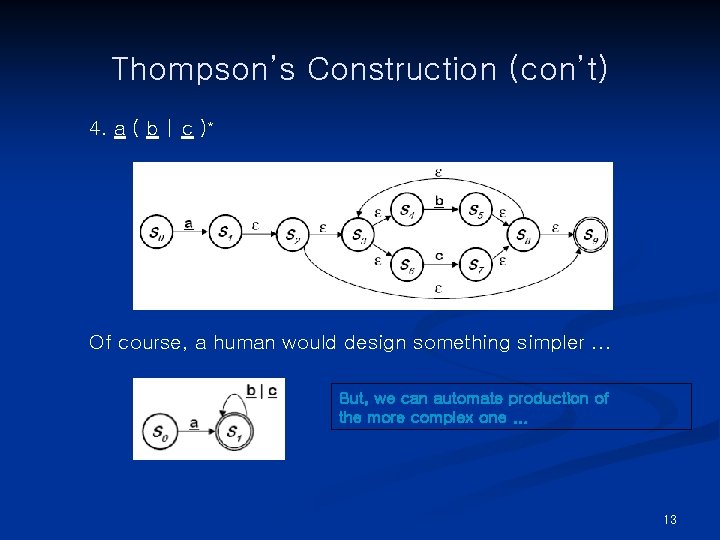
Thompson’s Construction Let’s try a ( b | c )* 1. a, b, & c 2. b | c 3. ( b | c )* 12

Thompson’s Construction (con’t) 4. a ( b | c )* Of course, a human would design something simpler. . . But, we can automate production of the more complex one. . . 13

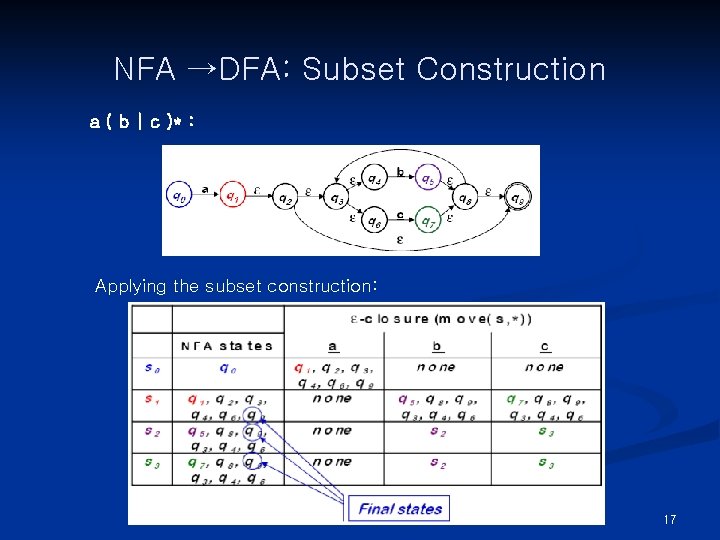
NFA →DFA: Subset Construction Need to build a simulation of the NFA Two key functions n Move(si , a) is set of states reachable from si by a n ε-closure(si) is set of states reachable from si by ε The algorithm: n Start state derived from s 0 of the NFA n Take its ε-closure S 0 = ε-closure(s 0) n Take the image of S 0, Move(S 0, α) for each α ∈ Σ, and take its ε-closure n Iterate until no more states are added Sounds more complex than it is… 14

NFA →DFA: Subset Construction The algorithm: s 0 ← ε-closure(q 0 n ) while ( S is still changing ) for each si ∈ S for each α ∈ Σ s? ←ε-closure(Move(si, α)) if ( s? ∉ S ) then add s? to S as sj T[si, α] ← sj Let’s think about why this works The algorithm halts: 1. S contains no duplicates (test before adding) 2. 2 Qn is finite 3. while loop adds to S, but does not remove from S (monotone) ⇒ the loop halts S contains all the reachable NFA states It tries each character in each si. It builds every possible NFA configuration. ⇒ S and T form the DFA 15

NFA →DFA: Subset Construction Example of a fixed-point computation n Monotone construction of some finite set n Halts when it stops adding to the set n Proofs of halting & correctness are similar n These computations arise in many contexts Other fixed-point computations n Canonical construction of sets of LR(1) items n n Quite similar to the subset construction Classic data-flow analysis (& Gaussian Elimination) n Solving sets of simultaneous set equations We will see many more fixed-point computations 16

NFA →DFA: Subset Construction a ( b | c )* : Applying the subset construction: 17

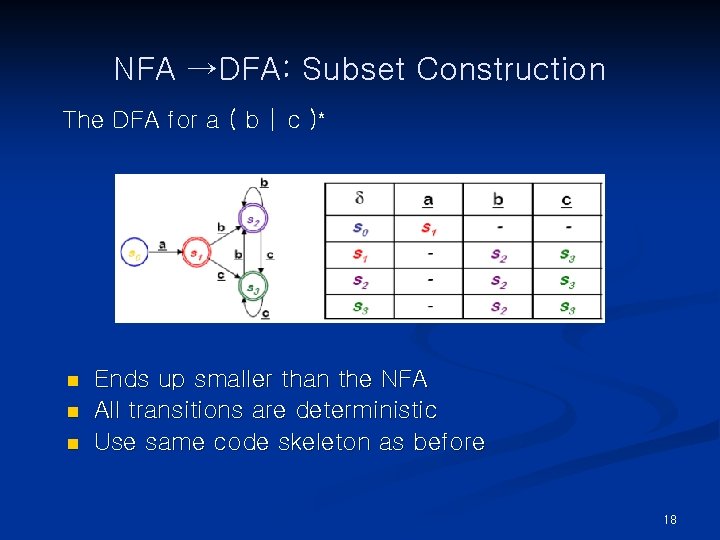
NFA →DFA: Subset Construction The DFA for a ( b | c )* n n n Ends up smaller than the NFA All transitions are deterministic Use same code skeleton as before 18

DFA Minimization The Big Picture n Discover sets of equivalent states n Represent each such set with just one state 19

DFA Minimization The Big Picture n Discover sets of equivalent states n Represent each such set with just one state Two states are equivalent if and only if: n The set of paths leading to them are equivalent n ∀ α ∈ Σ, transitions on α lead to equivalent states (DFA) n α-transitions to distinct sets ⇒ states must be in distinct sets 20

DFA Minimization The Big Picture n Discover sets of equivalent states n Represent each such set with just one state Two states are equivalent if and only if: n The set of paths leading to them are equivalent n ∀ α ∈ Σ, transitions on α lead to equivalent states (DFA) n α-transitions to distinct sets ⇒ states must be in distinct sets A partition P of S n Each s ∈ S is in exactly one set pi ∈ P n The algorithm iteratively partitions the DFA’s states 21

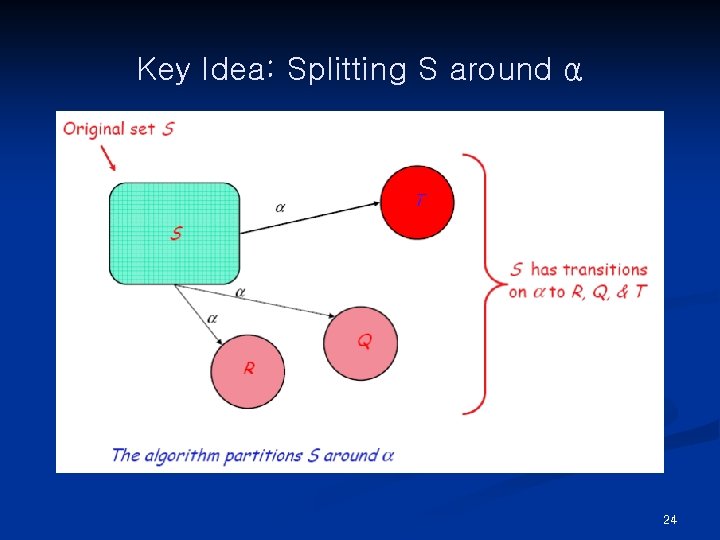
DFA Minimization Details of the algorithm n Group states into maximal size sets, optimistically n Iteratively subdivide those sets, as needed n States that remain grouped together are equivalent Initial partition, P 0 , has two sets: {F} & {Q-F} (D =(Q, Σ, δ, q 0, F)) Splitting a set (“partitioning a set by a”) n Assume qa, & qb ∈ s, and δ(qa, a) = qx, & δ(qb, a) = qy n If qx & qy are not in the same set, then s must be split n n qa has transition on a, qb does not ⇒ a splits s One state in the final DFA cannot have two transitions on a 22

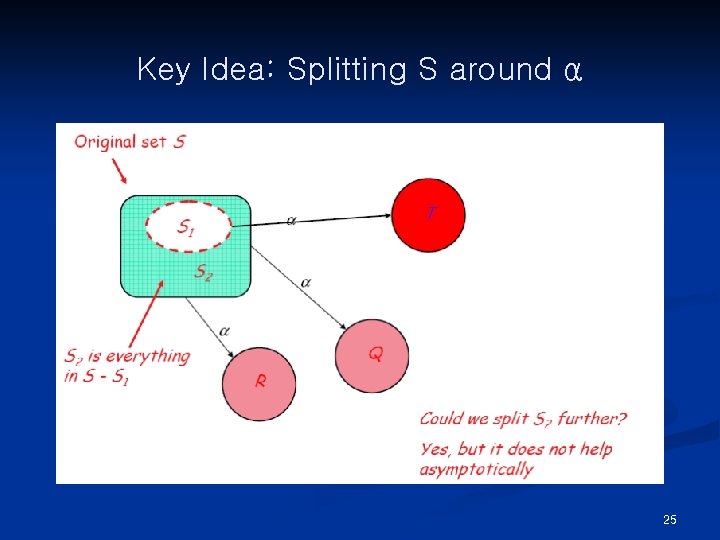
DFA Minimization The algorithm P ← { F, {Q-F}} while ( P is still changing) T←{} for each set S ∈ P for each α ∈ Σ partition S by α into S 1, and S 2 T ← T ∪ S 1 ∪ S 2 if T ≠ P then P←T Why does this work? n Partition P ∈ 2 Q n Start off with 2 subsets of Q {F} and {Q-F} n While loop takes Pi→Pi+1 by splitting 1 or more sets n Pi+1 is at least one step closer to the partition with |Q| sets n Maximum of |Q | splits Note that n Partitions are never combined n Initial partition ensures that final states are intact This is a fixed-point algorithm! 23

Key Idea: Splitting S around α 24

Key Idea: Splitting S around α 25

DFA Minimization Refining the algorithm n As written, it examines every S ∈ P on each iteration n This does a lot of unnecessary work Only need to examine S if some T, reachable from S, has split Reformulate the algorithm using a “worklist” n n Start worklist with initial partition, F and {Q-F} When it splits S into S 1 and S 2, place S 2 on worklist This version looks at each S ∈ P many fewer times ⇒ Well-known, widely used algorithm due to John Hopcroft 26

Hopcroft's Algorithm W ← {F, Q-F}; P ← {F, Q-F}; // W is the worklist, P the current partition while ( W is not empty ) do begin select and remove S from W; // S is a set of states for each α in Σ do begin let Iα← δα– 1( S ); // Iα is set of all states that can reach S on α for each R in P such that R ∩ Iα is not empty and R is not contained in Iα do begin partition R into R 1 and R 2 such that R 1← R ∩ Iχ ; R 2← R - R 1; replace R in P with R 1 and R 2 ; if R ∈ W then replace R with R 1 in W and add R 2 to W ; else if || R 1 || ≤ || R 2 || then add R 1 to W ; else add R 2 to W ; end end 27

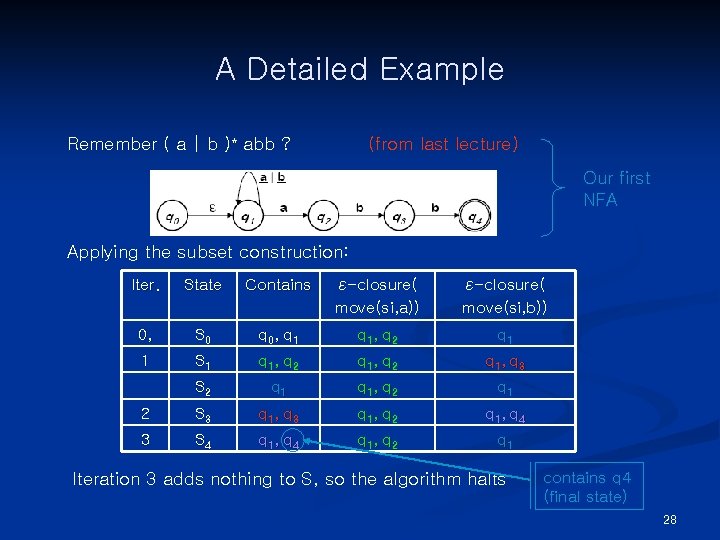
A Detailed Example Remember ( a | b )* abb ? (from last lecture) Our first NFA Applying the subset construction: Iter. State Contains ε-closure( move(si, a)) ε-closure( move(si, b)) 0, S 0 q 0 , q 1 , q 2 q 1 1 S 1 q 1 , q 2 q 1 , q 3 S 2 q 1 , q 2 q 1 2 S 3 q 1 , q 2 q 1 , q 4 3 S 4 q 1 , q 2 q 1 Iteration 3 adds nothing to S, so the algorithm halts contains q 4 (final state) 28

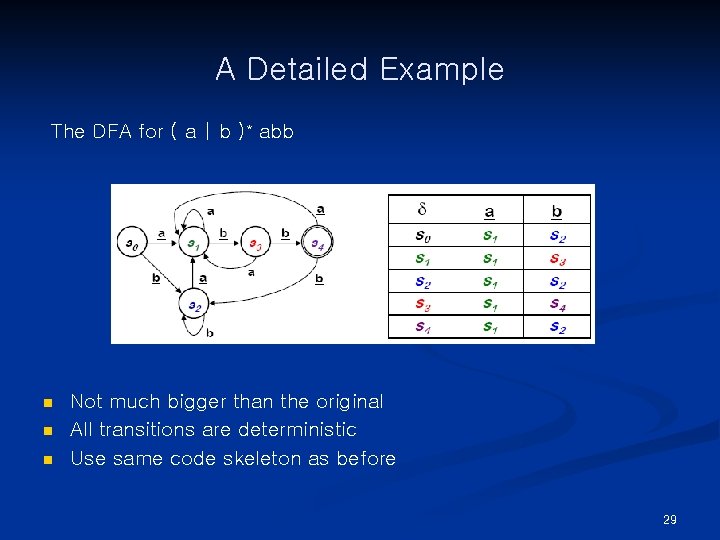
A Detailed Example The DFA for ( a | b )* abb n n n Not much bigger than the original All transitions are deterministic Use same code skeleton as before 29

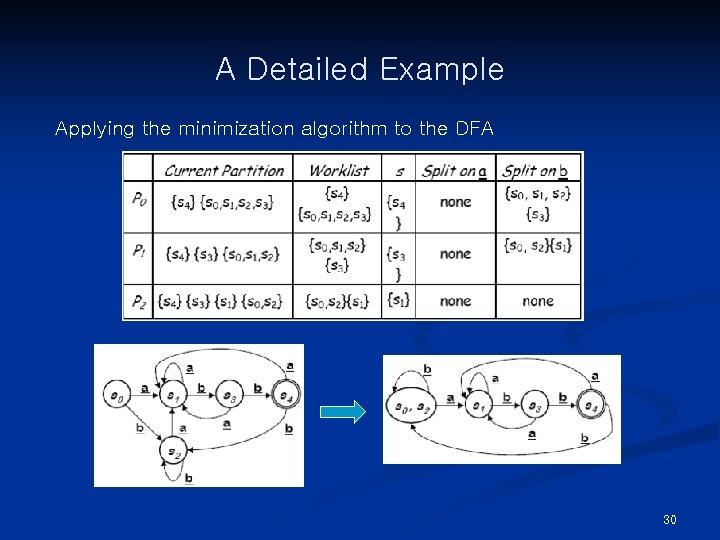
A Detailed Example Applying the minimization algorithm to the DFA 30

DFA Minimization What about a ( b | c )* ? First, the subset construction: 31

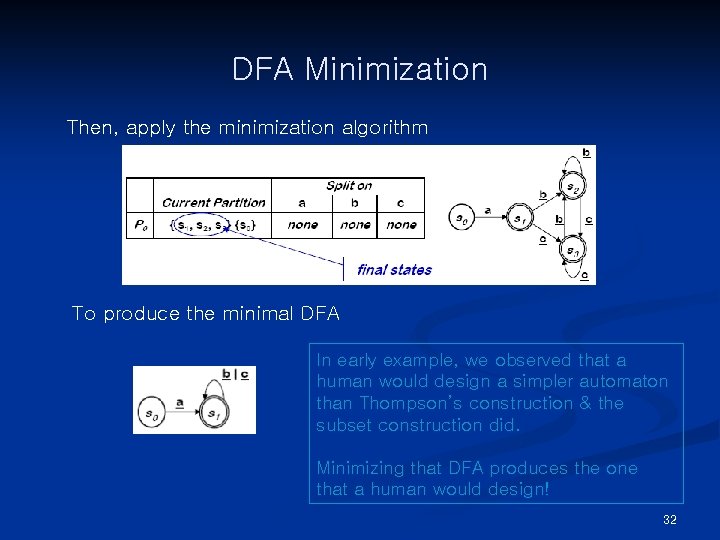
DFA Minimization Then, apply the minimization algorithm To produce the minimal DFA In early example, we observed that a human would design a simpler automaton than Thompson’s construction & the subset construction did. Minimizing that DFA produces the one that a human would design! 32

Example of the partitioning procedures M: 0 1 A B, 0 C, 0 B C, 1 D, 1 C D, 0 E, 0 D C, 1 B, 1 E F, 1 E, 1 F G, 0 C, 0 G F, 1 G, 1 H J, 1 B, 0 J H, 1 D, 0 P 1: {A, C, F}, {B, D, E, G}, {H, J} 1 1 P 2: {A, F}, {C}, {B, D, E, G}, {H, J} 0 0 P 3: {A, F}, {C}, {B, D}, {E, G}, {H, J} 0 0 P 4: {A}, {F}, {C}, {B, D}, {E, G}, {H, J} 33

Abbreviated Register Specification Start with a regular expression r 0 | r 1 | r 2 | r 3 | r 4 | r 5 | r 6 | r 7 | r 8 | r 9 34

Abbreviated Register Specification Thompson’s construction produces To make it fit, we’ve eliminated the ε-transition between “r” and “ 0”. 35

Abbreviated Register Specification The subset construction builds This is a DFA, but it has a lot of states … 36

Abbreviated Register Specification The DFA minimization algorithm builds This looks like what a skilled compiler writer would do! 37

Limits of Regular Languages Advantages of Regular Expressions n Simple & powerful notation for specifying patterns n Automatic construction of fast recognizers n Many kinds of syntax can be specified with REs Example — an expression grammar Term → [a-z. A-Z] ([a-z. A-z] | [0 -9])* Op → + | - | ∗ | / Expr → ( Term Op )* Term Of course, this would generate a DFA … If REs are so useful … Why not use them for everything? 38

Limits of Regular Languages Not all languages are regular RL’s ⊂ CFL’s ⊂ CSL’s You cannot construct DFA’s to recognize these languages n L = { pk qk } (parenthesis languages) n L = { wcwr | w ∈ Σ*} Neither of these is a regular language (nor an RE) But, this is a little subtle. You can construct DFA’s for n Strings with alternating 0’s and 1’s ( ε | 1 ) ( 01 )* ( ε | 0 ) n Strings with and even number of 0’s and 1’s See Homework 1! RE’s can count bounded sets and bounded differences 39

What Can Be So Hard? Poor language design can complicate scanning n Reserved words are important if then = else; else = then (PL/I) n Insignificant blanks (Fortran & Algol 68) do 10 i = 1, 25 do 10 i = 1. 25 n n String constants with special characters (C, C++, Java, …) newline, tab, quote, comment delimiters, … Finite closures (Fortran 66 & Basic) n n Limited identifier length Adds states to count length 40

Building Faster Scanners from DFA Table-driven recognizers waste effort n Read (& classify) the next character n Find the next state n Assign to the state variable n Trip through case logic in action() n Branch back to the top We can do better n Encode state & actions in the code n Do transition tests locally n Generate ugly, spaghetti-like code n Takes (many) fewer operations per input character 41

Building Faster Scanners from DFA A direct-coded recognizer for r Digit* goto s 0; s 0: word ← Ø; char ← next character; if (char = ‘r’) then goto s 1; else goto se; s 1: word ← word + char; char ← next character; if (‘ 0’ ≤ char ≤ ‘ 9’) then goto s 2; else goto se; n n n s 2: word ← word + char; char ← next character; if (‘ 0’ ≤ char ≤ ‘ 9’) then goto s 2; else if (char = eof) then report success; else goto se; se: print error message; return failure; Many fewer operations per character Almost no memory operations Even faster with careful use of fall-through cases 42

Building Faster Scanners Hashing keywords versus encoding them directly n Some (well-known) compilers recognize keywords as identifiers and check them in a hash table n Encoding keywords in the DFA is a better idea n n O(1) cost per transition Avoids hash lookup on each identifier 43

Building Scanners The point n All this technology lets us automate scanner construction n Implementer writes down the regular expressions n Scanner generator builds NFA, DFA, minimal DFA, and then writes out the (table-driven or direct-coded) code n This reliably produces fast, robust scanners For most modern language features, this works n You should think twice before introducing a feature that defeats a DFA-based scanner n The ones we’ve seen (e. g. , insignificant blanks, nonreserved keywords) have not proven particularly useful or long lasting 44

Some Points n Table-driven scanners are not fast n n Faster code can be generated by embedding scanner in code n n Ea. C doesn’t say they are slow; it says you can do better This was shown for both LR-style parsers and for scanners in the 1980 s Hashed lookup of keywords is slow n Ea. C doesn’t say it is slow. It says that the effort can be folded into the scanner so that it has no extra cost. Compilers like GCC use hash lookup. A word must fail in the lookup to be classified as an identifier. With collisions in the table, this can add up. At any rate, the cost is unneeded, since the DFA can do it for O(1) cost per character. 45

Summary n Theory of lexical analysis n n n RE NFA DFA → NFA: Thompson's construction → DFA: Subset construction → Minimal DFA: Hopcroft’s algorithm → RE: paths on DFA graph Building scanners 46

Next Class n Introduction to Parsing n n Context-free grammars and derivations Top-down parsing 47

Questions 48