Chapter 2 Finite Automata 1 A FiniteState Machine

Chapter 2 Finite Automata 1

A Finite-State Machine (1) m A finite state machine is a mathematical model of a system, with discrete inputs and outputs 2

A Finite-State Machine (2) m Finite Automata FA: q a finite set of states q a set of transitions (edges) q a start state q a set of final states Defining a FA is a kind of programming. m m m Problem definition q Includes defining possible actions & accepting condition. States structure of program q Includes designating which are initial & final. Transitions program 3

2. 1: Deterministic Finite Automata (1) m DFA M = (Q, S, , q 0, F) q Q = a finite set of states q S = a finite set called the alphabet q = transition function Ø total function Q S Q q q 0 = start state q 0 Q q F = final or accepting states F Q 4

Deterministic Finite Automata (2) m DFA M q Q = {q 0, q 1} q S = {a, b} q F = {q 1} q The transition function is given in a tabular form called the transition table q (q 0, a) = q 1 (q 0, b) = q 0 q (q 1, a) = q 1 (q 1, b) = q 0 5

Deterministic Finite Automata (3) m A DFA M can be considered to be a language acceptor. m The language of M, L(M), is the set of strings S* accepted by M. m A DFA M reads an input string from left to right. m The next state depends on the current state and the unread (unprocessed) symbol. 6

Deterministic Finite Automata (5) m m m The DFA M accepts the set of strings over {a, b} that contain the substring bb q M : Q = {q 0, q 1, q 2}, S = {a, b}, F = {q 2} q The transition function is given in a tabular form called the transition table q (q 0, a) = q 0 (q 0, b) = q 1 q (q 1, a) = q 0 (q 1, b) = q 2 q (q 2, a) = q 2 (q 2, b) = q 2 Is abba L(M)? Yes, since the computation halts in state q 2, which is a final state Is abab L(M)? No, since the computation halts in state q 1, which is NOT a final state 7

Deterministic Finite Automata (6) m Extended transition function * of a DFA with transition function is a function from Q S* Q defined recursively on the length of the input string w q Basis: |w| = 0. Then w = and *(qi, ) = qi q Recursive step: Let |w| = 1. Then *(qi, av) = *( (qi, a), v) q qi Q, a S, v S* 8

Deterministic Finite Automata (7) m A string w is accepted if *(q 0, w) F m The language of a DFA M is q L(M) = {w S* | *(q 0, w) F} m DFA M = (Q, S, , q 0, F) accepts w S* q *(q 0, w) F 9

Deterministic Finite Automata (8) m Two possibilities for DFA M running on w q M accepts w Ø M accepts w iff the computation of M on w ends up (halts) in an accepting configuration Ø *(q 0, w) F q M rejects w Ø M rejects w iff the computation of M on w ends up (halts) in a rejecting configuration Ø *(q 0, w) F 10

State Diagrams and Examples (1) m The state diagram of a DFA M = (Q, S, , q 0, F) is a labeled graph G defined by the following conditions: q The nodes of G are the elements of Q q The labels on the arcs of G are elements of a q q q 0 is the start node, denoted by F is the set of accepting nodes, denoted by There is an arc from node qi to qj labeled a if (qi, a) = qj For every node qi and symbol a S, there is exactly one arc labeled a leaving qi 11

State Diagrams and Examples (2) m Deterministic Finite Automata DFA q all outgoing edges are labelled with an input character Ø no state has - transition, transition on input q no two edges leaving a given state have the same label Ø for each state s and input symbol a, there is at most one edge label a leaving s q Therefore: the next state can be determined uniquely, given the current state and the current input character 12

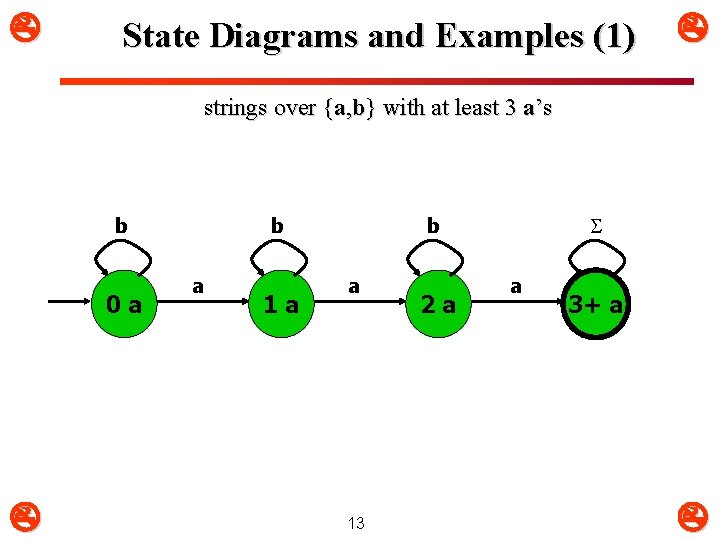
State Diagrams and Examples (1) strings over {a, b} with at least 3 a’s b 0 a b a 1 a S b a 13 2 a a 3+ a

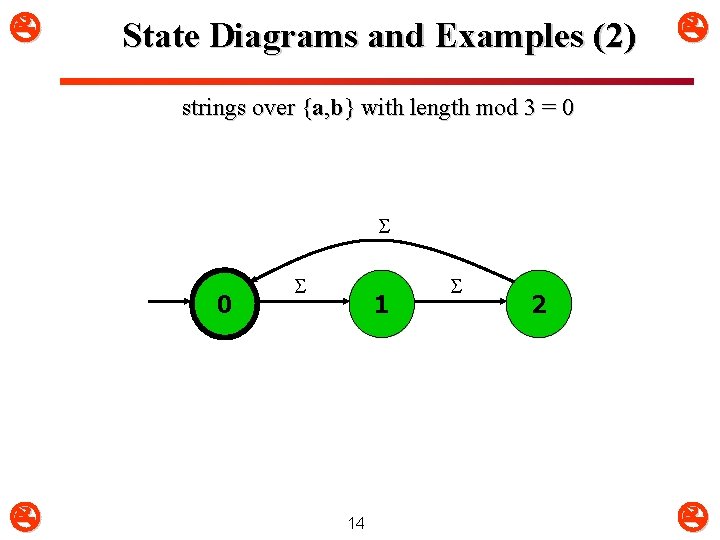
State Diagrams and Examples (2) strings over {a, b} with length mod 3 = 0 S 1 14 S 2

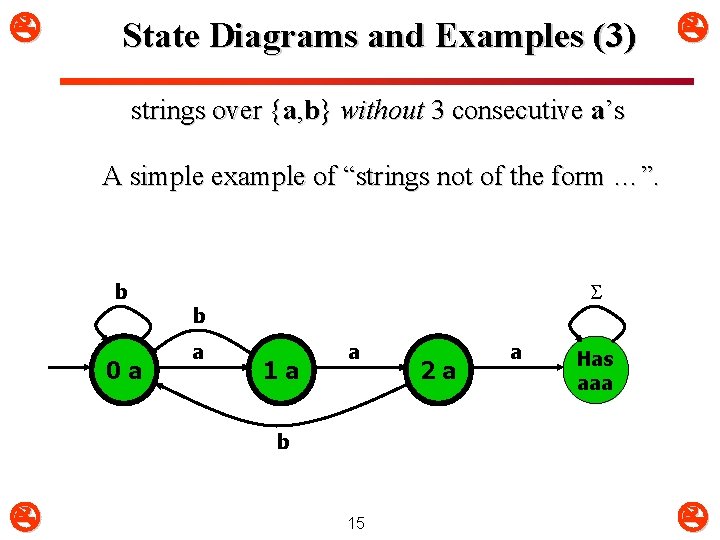
State Diagrams and Examples (3) strings over {a, b} without 3 consecutive a’s A simple example of “strings not of the form …”. b 0 a S b a 1 a a 2 a a Has aaa b 15

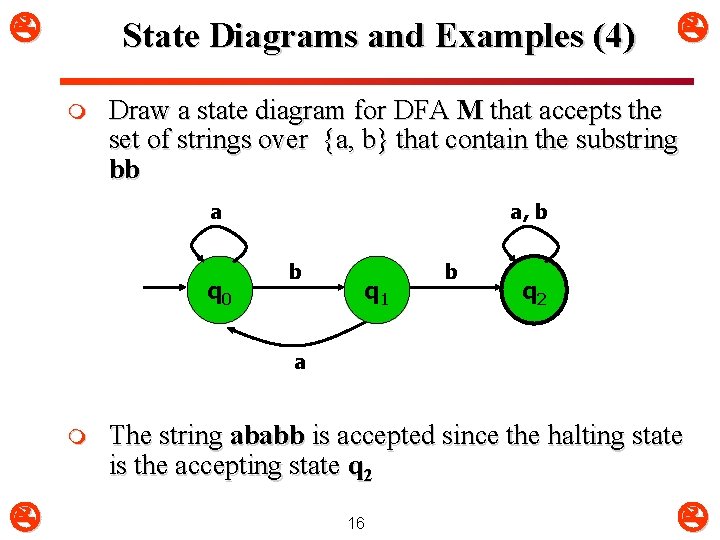
State Diagrams and Examples (4) m Draw a state diagram for DFA M that accepts the set of strings over {a, b} that contain the substring bb a q 0 a, b b q 1 b q 2 a m The string ababb is accepted since the halting state is the accepting state q 2 16

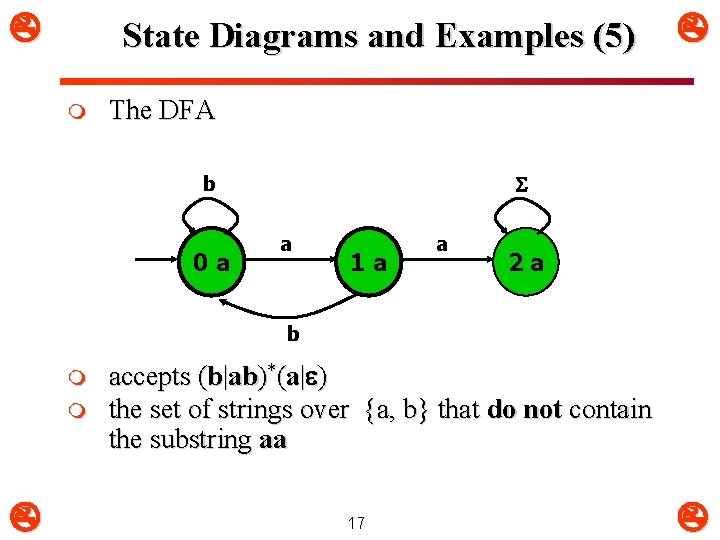
State Diagrams and Examples (5) m The DFA b 0 a a 1 a a 2 a b m m accepts (b|ab)*(a| ) the set of strings over {a, b} that do not contain the substring aa 17

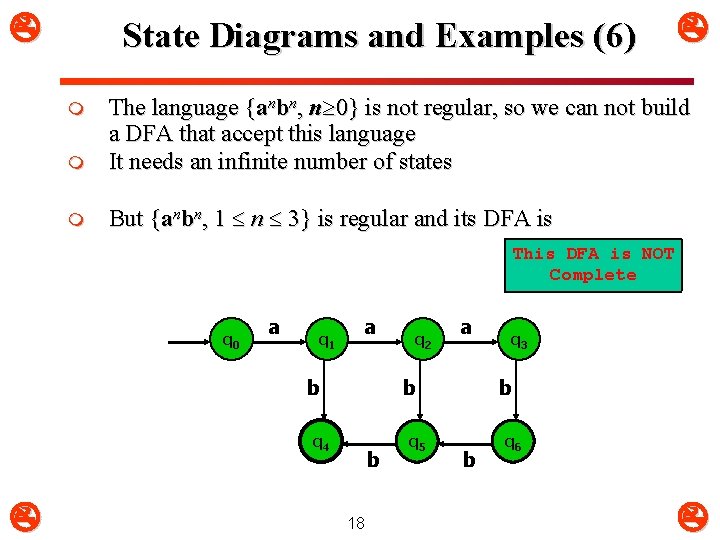
State Diagrams and Examples (6) m The language {anbn, n 0} is not regular, so we can not build a DFA that accept this language It needs an infinite number of states m But {anbn, 1 n 3} is regular and its DFA is m This DFA is NOT Complete q 0 a q 1 a b q 4 q 2 b 18 q 5 q 3 b b q 6

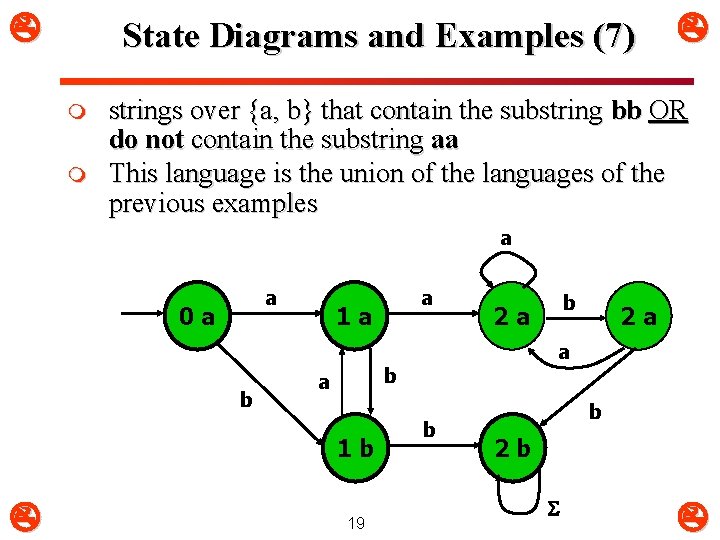
State Diagrams and Examples (7) m m strings over {a, b} that contain the substring bb OR do not contain the substring aa This language is the union of the languages of the previous examples a a 0 a b 1 a b 2 a 19 2 a a b a 1 b a b b 2 b

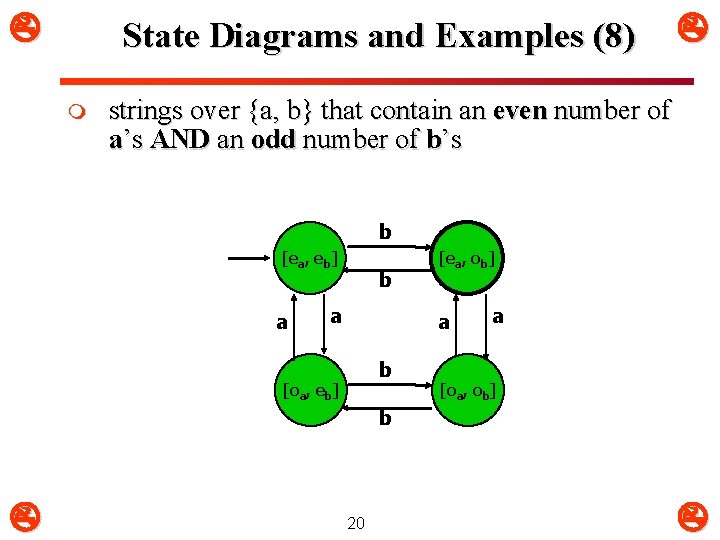
State Diagrams and Examples (8) m strings over {a, b} that contain an even number of a’s AND an odd number of b’s b [ea, eb] a b a [ea, ob] a b [oa, eb] a [oa, ob] b 20

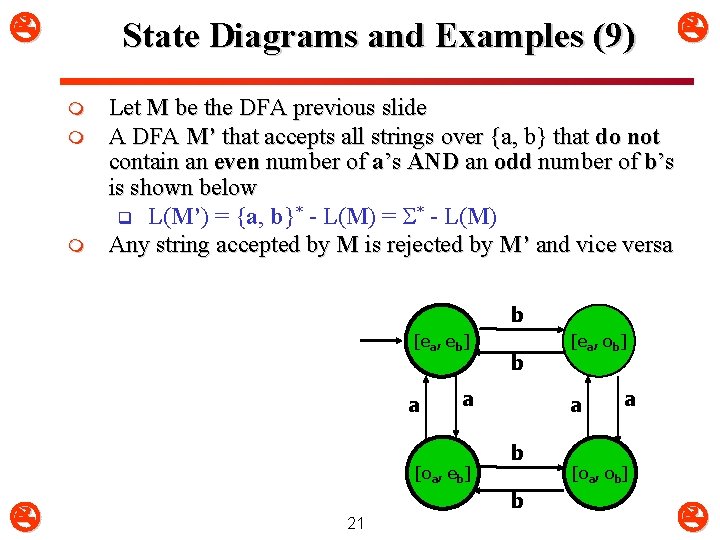
State Diagrams and Examples (9) m m m Let M be the DFA previous slide A DFA M’ that accepts all strings over {a, b} that do not contain an even number of a’s AND an odd number of b’s is shown below q L(M’) = {a, b}* - L(M) = S* - L(M) Any string accepted by M is rejected by M’ and vice versa b [ea, eb] a a [oa, eb] b a b b 21 [ea, ob] a [oa, ob]

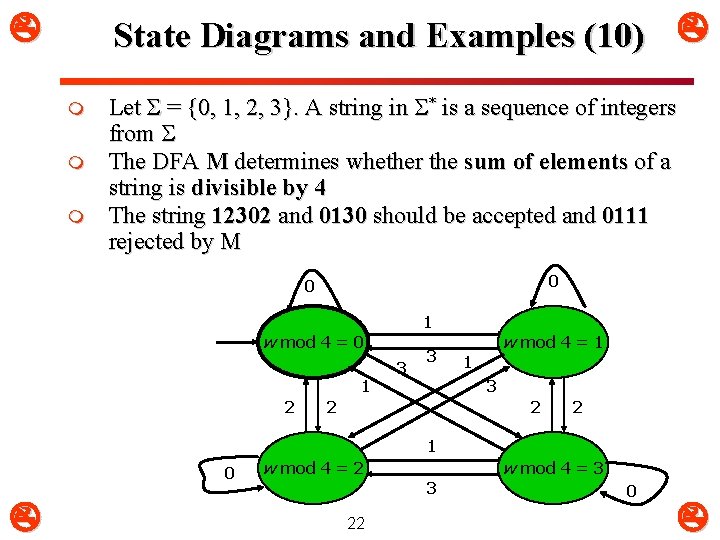
State Diagrams and Examples (10) m m m Let S = {0, 1, 2, 3}. A string in S* is a sequence of integers from S The DFA M determines whether the sum of elements of a string is divisible by 4 The string 12302 and 0130 should be accepted and 0111 rejected by M 0 0 1 w mod 4 = 0 1 2 3 3 w mod 4 = 1 1 3 2 2 2 1 0 w mod 4 = 2 22 3 w mod 4 = 3 0

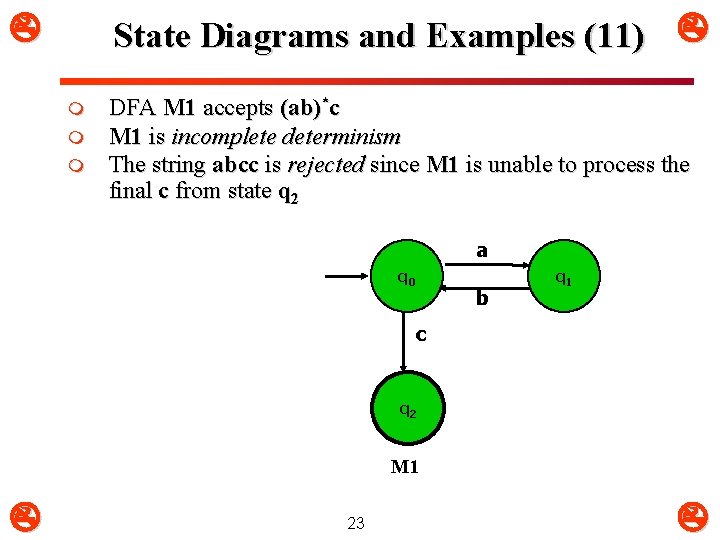
State Diagrams and Examples (11) m m m DFA M 1 accepts (ab)*c M 1 is incomplete determinism The string abcc is rejected since M 1 is unable to process the final c from state q 2 a q 0 b q 1 c q 2 M 1 23

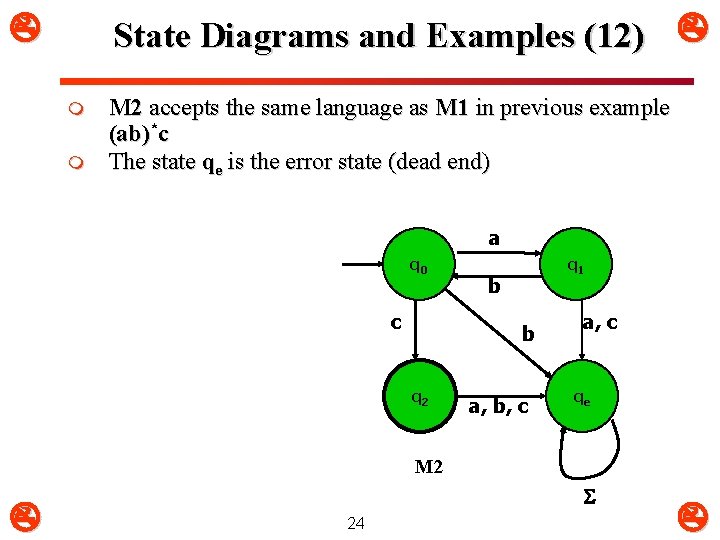
State Diagrams and Examples (12) m m M 2 accepts the same language as M 1 in previous example (ab)*c The state qe is the error state (dead end) a q 0 c q 1 b b q 2 a, b, c a, c qe M 2 24

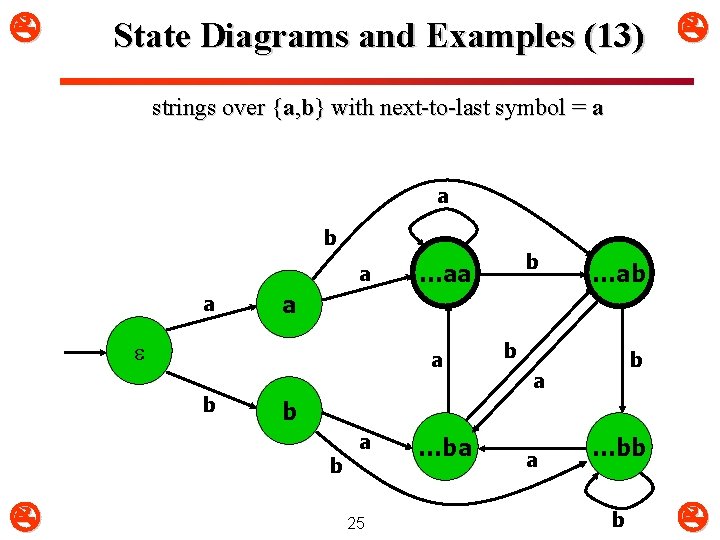
State Diagrams and Examples (13) strings over {a, b} with next-to-last symbol = a a b a a a b b …ab a b b …aa a 25 …ba a …bb b

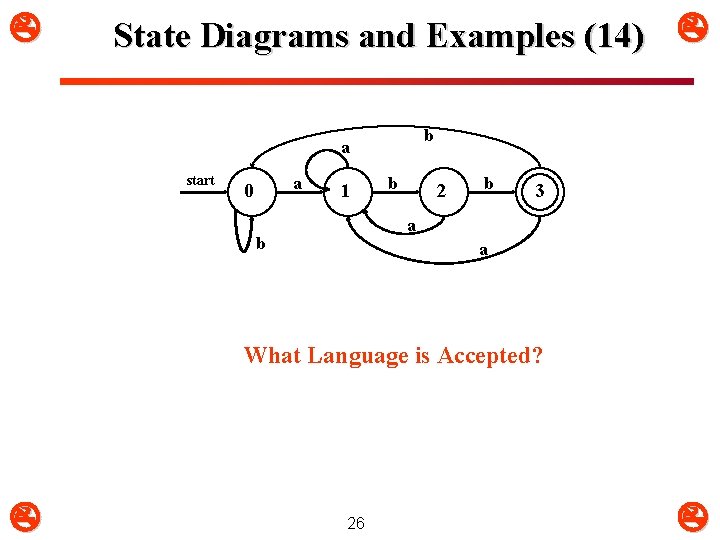
State Diagrams and Examples (14) b a start a 0 1 b 2 b 3 a b a What Language is Accepted? 26

2. 2: Nondeterministic Finite Automata (1) Finite Automata : A recognizer that takes an input string & determines whether it’s a valid sentence of the language Deterministic : Has at most one action for every given input symbol. Non-Deterministic : Has more than one (or no) alternative action for the same input symbol. 27

Nondeterministic Finite Automata (2) NFA: Formal Definition m NFA M = (Q, S, , q 0, F) q q q Q = a finite set of states S = a finite set alphabet = transition function Ø total function Q S (Q) = 2 Q - power set of Q q q q 0 = initial/starting state F = final or accepting states 28 q 0 Q F Q

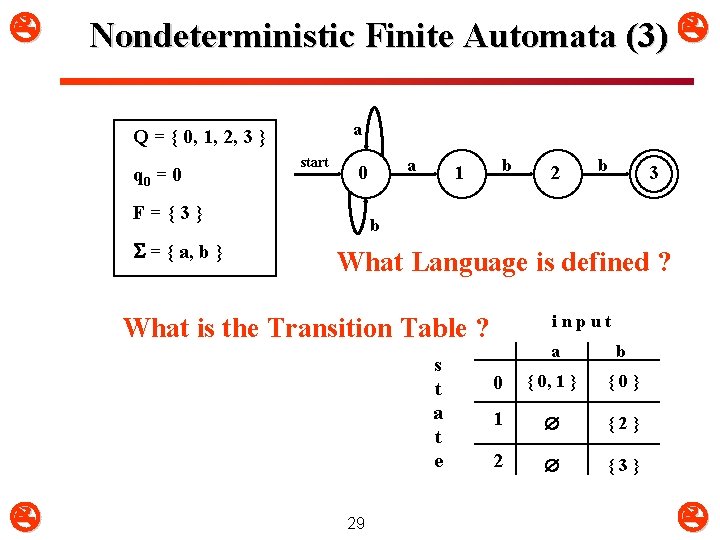
Nondeterministic Finite Automata (3) a Q = { 0, 1, 2, 3 } q 0 = 0 start F={3} = { a, b } a 0 1 b b 3 b What Language is defined ? input What is the Transition Table ? s t a t e 2 29 a b 0 { 0, 1 } {0} 1 {2} 2 {3}

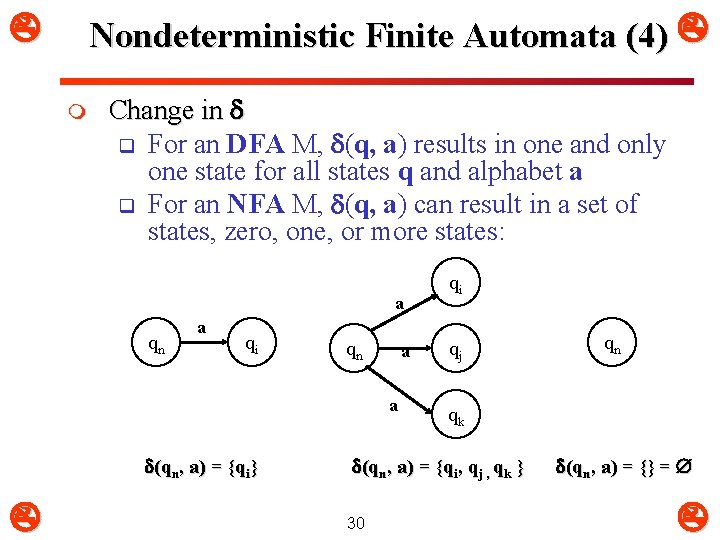
Nondeterministic Finite Automata (4) m Change in q For an DFA M, (q, a) results in one and only one state for all states q and alphabet a q For an NFA M, (q, a) can result in a set of states, zero, one, or more states: a qn a qi qn a a (qn, a) = {qi} qi qj qk (qn, a) = {qi, qj , qk } 30 qn (qn, a) = {} =

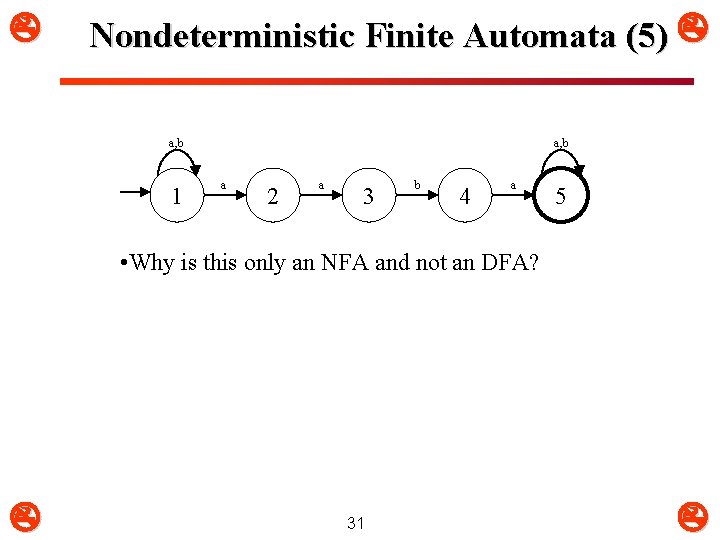
Nondeterministic Finite Automata (5) a, b 1 a, b a 2 a 3 b 4 a 5 • Why is this only an NFA and not an DFA? 31

Nondeterministic Finite Automata (6) Computing with NFA’s m Computations are different m We always start from start state. Call it the root of the computation. m Then we might go to different states on one symbol. m Then from those states to new sets of states, creating a tree-like computation. m If one path ends up in a final state, then ACCEPT, else REJECT 32

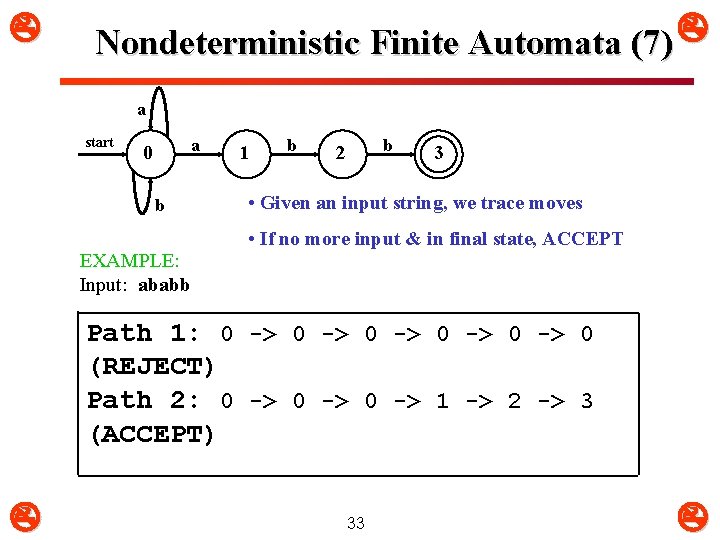
Nondeterministic Finite Automata (7) a start a 0 b EXAMPLE: Input: ababb 1 b b 2 3 • Given an input string, we trace moves • If no more input & in final state, ACCEPT Path 1: 0 -> 0 -> 0 (REJECT) Path 2: 0 -> 1 -> 2 -> 3 (ACCEPT) 33

Nondeterministic Finite Automata (8) m m Extended transition function * of a NFA with transition function is a function from Q S* 2 Q (power set) defined recursively on the length of the input string w q Basis: |w| = 0. Then w = and *(qi, ) = {qi} q Recursive step: Let |w| = 1. Then *(qi, av) = U *(qj, v), qj (qi, a) q qi Q, qj Q , a S, v S* The language of a NFA M is q L(M) = {w S* | *(q 0, w) F ≠ } 34

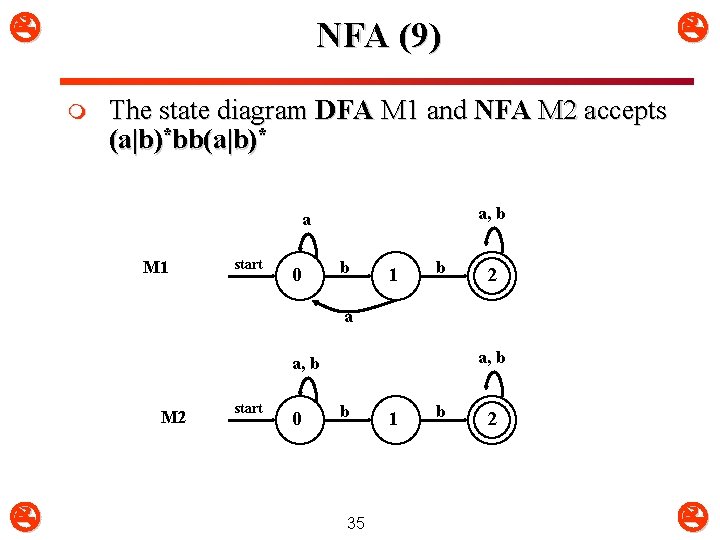
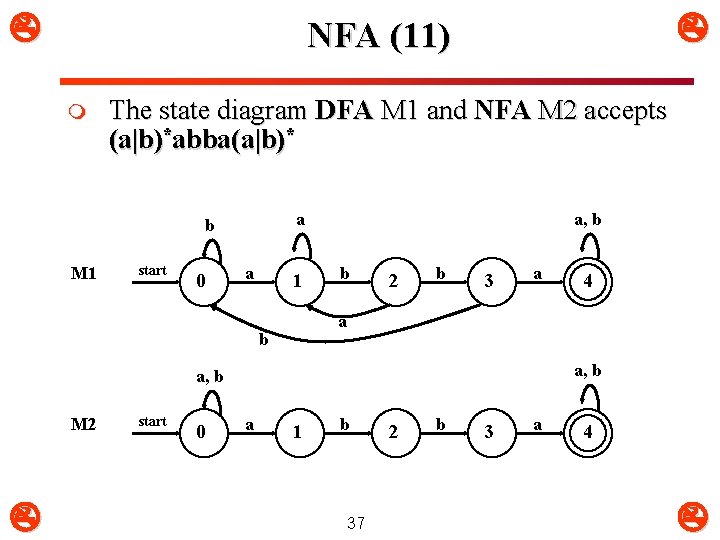
NFA (9) m The state diagram DFA M 1 and NFA M 2 accepts (a|b)*bb(a|b)* a, b a M 1 start 0 b 1 b 2 a a, b M 2 start 0 b 35 1 b 2

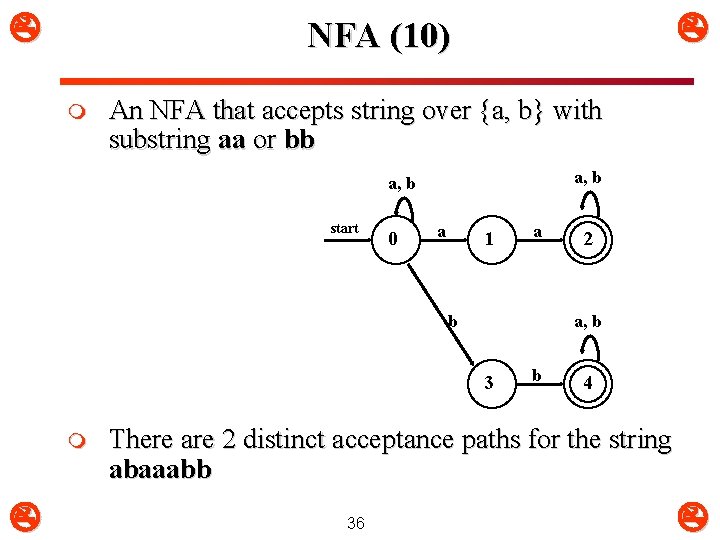
NFA (10) m An NFA that accepts string over {a, b} with substring aa or bb a, b start 0 a 1 a b a, b 3 m 2 b 4 There are 2 distinct acceptance paths for the string abaaabb 36

NFA (11) m The state diagram DFA M 1 and NFA M 2 accepts (a|b)*abba(a|b)* a b M 1 start 0 a 1 a, b b 2 b 3 a a b a, b M 2 start 0 4 a 1 b 37 2 b 3 a 4

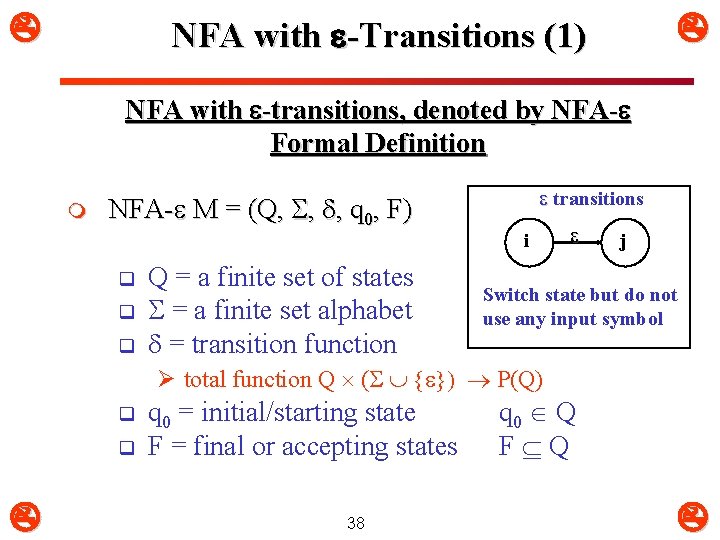
NFA with -Transitions (1) NFA with -transitions, denoted by NFA- Formal Definition m NFA- M = (Q, S, , q 0, F) q q q Q = a finite set of states S = a finite set alphabet = transition function transitions i j Switch state but do not use any input symbol Ø total function Q (S { }) (Q) q q q 0 = initial/starting state F = final or accepting states 38 q 0 Q F Q

-Transitions (2) m The input string w is accepted using NFA- if there is a computation that processes the entire string and halts in an accepting state m A computation may continue using -transition after the input string has been completely processed 39

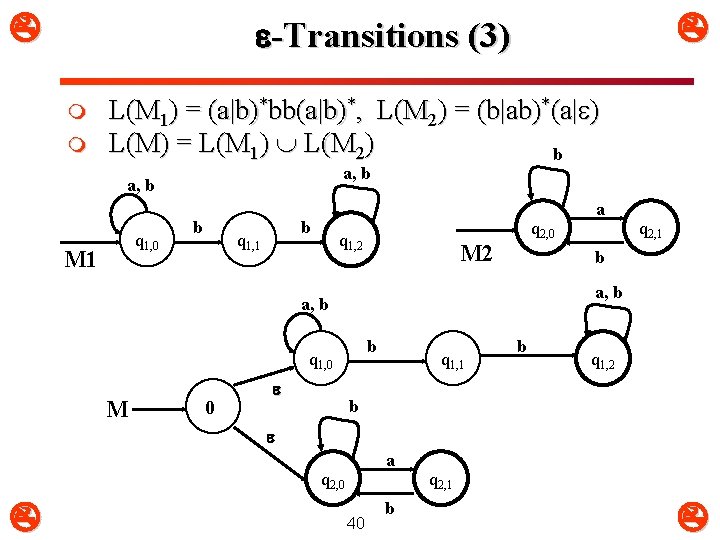
-Transitions (3) m m L(M 1) = (a|b)*bb(a|b)*, L(M 2) = (b|ab)*(a| ) L(M) = L(M 1) L(M 2) b a, b q 1, 0 M 1 b b q 1, 1 q 1, 2 q 2, 0 M 2 a, b b q 1, 0 M 0 q 2, 1 b a, b a q 1, 1 b q 1, 2 b a q 2, 0 40 b q 2, 1

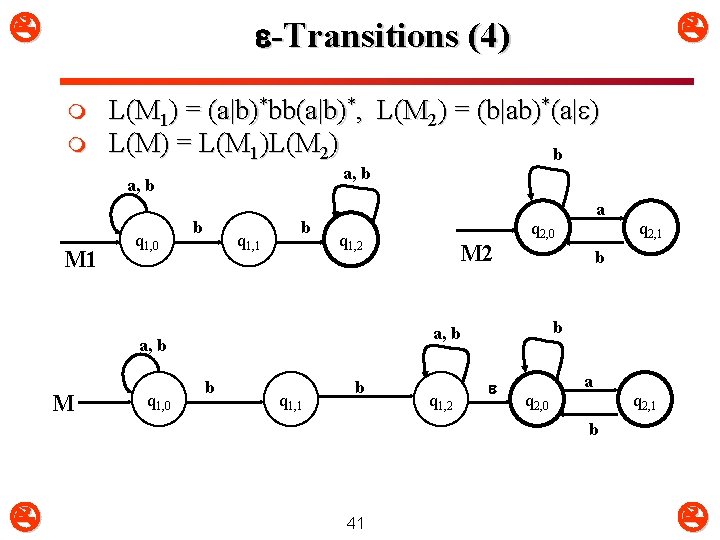
-Transitions (4) m m L(M 1) = (a|b)*bb(a|b)*, L(M 2) = (b|ab)*(a| ) L(M) = L(M 1)L(M 2) b a, b M 1 q 1, 0 b q 1, 1 b q 1, 2 q 1, 0 q 2, 0 b q 1, 1 b q 1, 2 q 2, 1 b b a, b M M 2 a q 2, 0 a q 2, 1 b 41

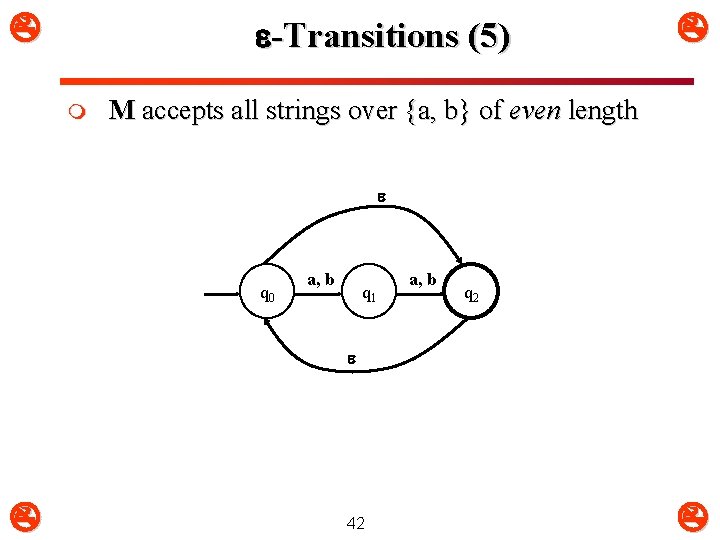
-Transitions (5) m M accepts all strings over {a, b} of even length q 0 a, b q 1 a, b q 2 42

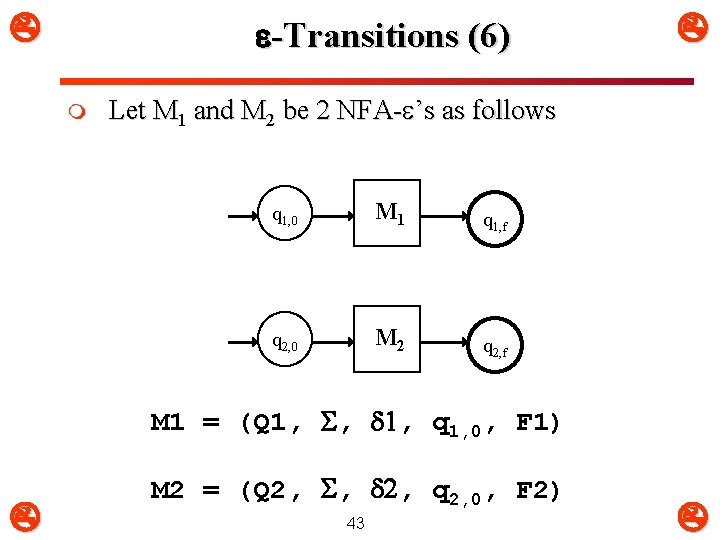
-Transitions (6) m Let M 1 and M 2 be 2 NFA- ’s as follows q 1, 0 M 1 q 1, f q 2, 0 M 2 q 2, f M 1 = (Q 1, , 1, q 1, 0, F 1) M 2 = (Q 2, , 2, q 2, 0, F 2) 43

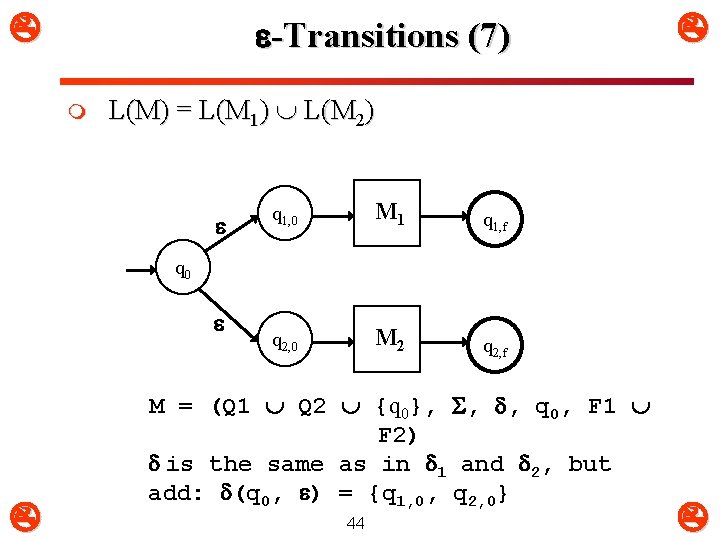
-Transitions (7) m L(M) = L(M 1) L(M 2) q 1, 0 M 1 q 1, f q 2, 0 M 2 q 2, f q 0 M = (Q 1 Q 2 {q 0}, , , q 0, F 1 F 2) is the same as in 1 and 2, but add: (q 0, ) = {q 1, 0, q 2, 0} 44

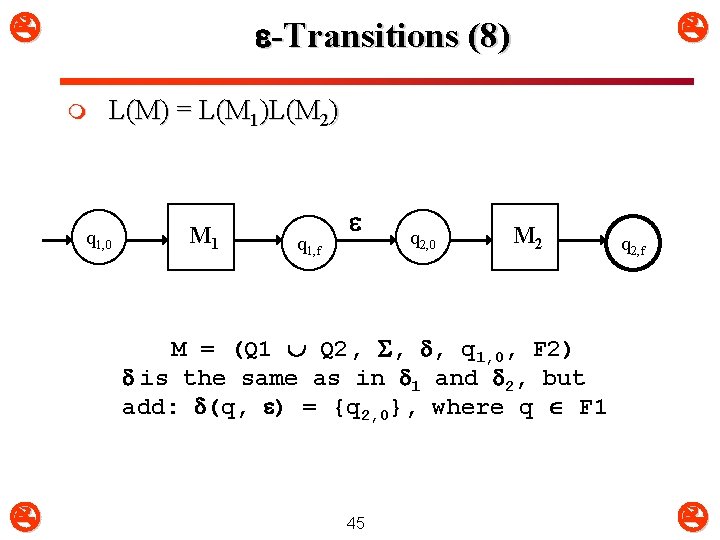
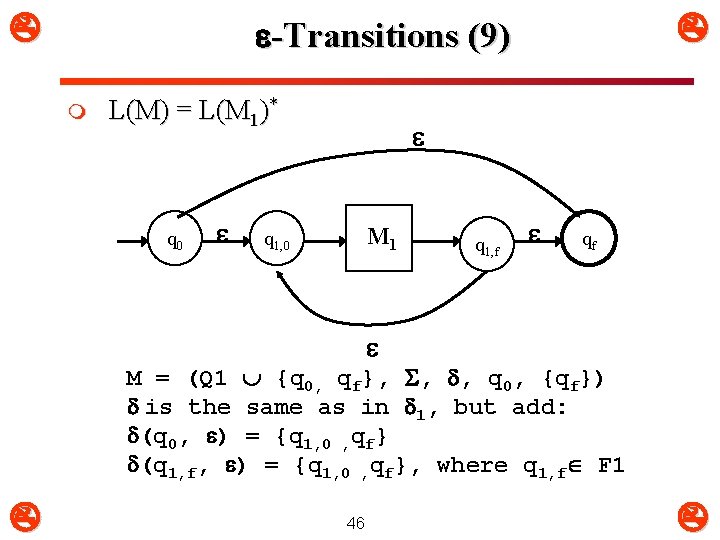
-Transitions (8) m L(M) = L(M 1)L(M 2) q 1, 0 M 1 q 1, f q 2, 0 M 2 q 2, f M = (Q 1 Q 2, , , q 1, 0, F 2) is the same as in 1 and 2, but add: (q, ) = {q 2, 0}, where q F 1 45

-Transitions (9) m L(M) = L(M 1)* q 0 M 1 q 1, 0 q 1, f qf M = (Q 1 {q 0, qf}, , , q 0, {qf}) is the same as in 1, but add: (q 0, ) = {q 1, 0 , qf} (q 1, f, ) = {q 1, 0 , qf}, where q 1, f F 1 46

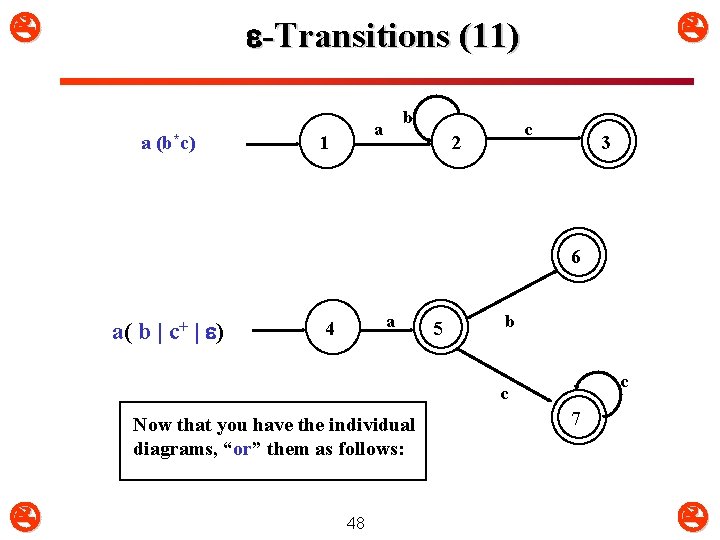
-Transitions (10) Given the regular expression : a(b*c) | a( b | c+ | ) Find a transition diagram NFA- that recognizes it. 47

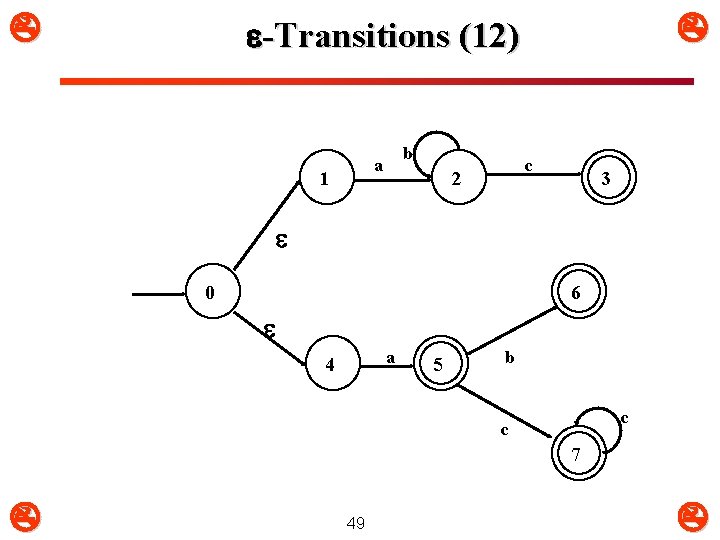
-Transitions (11) a (b*c) b a 1 c 2 3 6 a( b | c+ | ) a 4 5 b c c Now that you have the individual diagrams, “or” them as follows: 48 7

-Transitions (12) b a 1 c 2 3 6 0 a 4 5 b c c 7 49

-Transitions (12) m See examples 2. 7, 2. 8, 2. 9, and 2. 10 50

2. 3: Equivalence of DFA & NFA (1) m Is NFA more powerful than DFA? NO! q NFA inefficient to implement directly, so convert to a DFA that recognizes the same strings m Is there a language accepted by an NFA that is not accepted by any DFA? No m NFA is equivalent to DFA. q Each state in DFA corresponds to a SET of states of the NFA 51

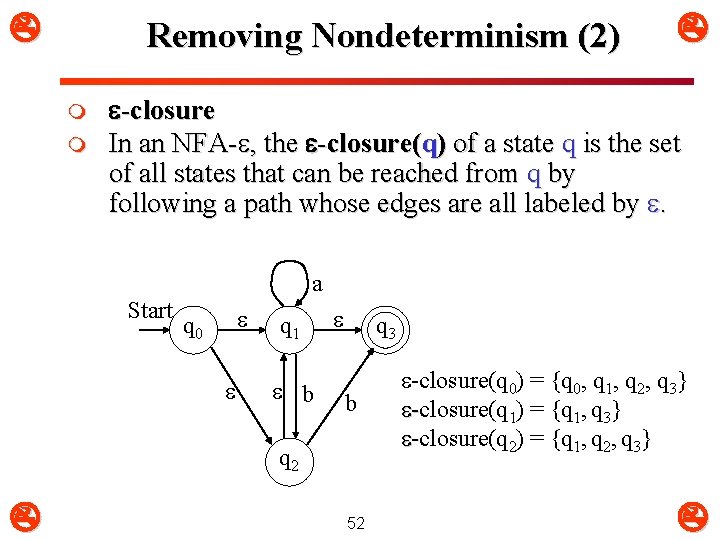
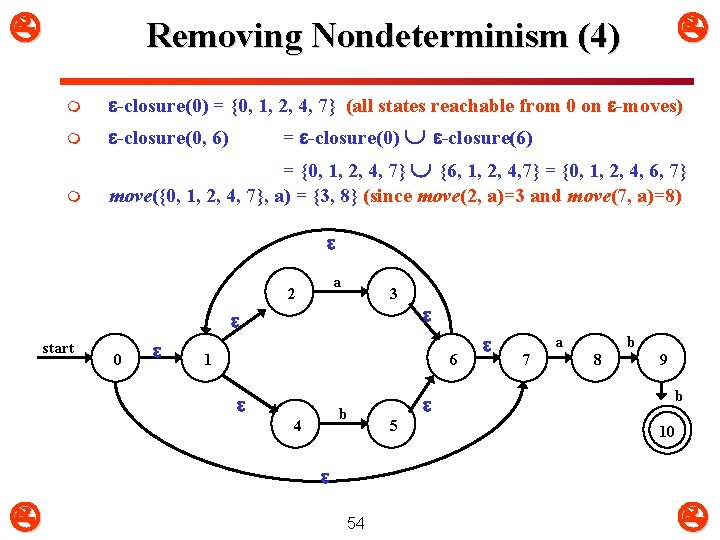
Removing Nondeterminism (2) m m -closure In an NFA- , the -closure(q) of a state q is the set of all states that can be reached from q by following a path whose edges are all labeled by . a Start q 0 q 1 b q 3 b q 2 52 -closure(q 0) = {q 0, q 1, q 2, q 3} -closure(q 1) = {q 1, q 3} -closure(q 2) = {q 1, q 2, q 3}

Removing Nondeterminism (3) NFA- -closure(q) : No input is consumed N = (Q, , , q 0, F) q Q : set of NFA- states that are reachable from q on -transitions only -closure(T) : T Q : NFA- states reachable from some state t T on -transitions only move(T, a) : T Q, a : set of states to which there is a transition on input a from some state t T move({q 1, q 2, …, qi}, a) = (q 1, a) (q 2, a) … (qi, a) These 3 operations are utilized by algorithms / techniques to facilitate the conversion process 53

Removing Nondeterminism (4) m -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves) m -closure(0, 6) m = {0, 1, 2, 4, 7} {6, 1, 2, 4, 7} = {0, 1, 2, 4, 6, 7} move({0, 1, 2, 4, 7}, a) = {3, 8} (since move(2, a)=3 and move(7, a)=8) = -closure(0) -closure(6) a 2 3 start 0 1 6 b 4 5 a 7 b 8 9 b 10 54

NFA- DFA with Subset Construction NFA- N DFA M construction: Given N = (Q, , , q 0, F), define M = (Q’, , ’, q’ 0, F’) Q’ P(Q), all the possible NFA- states M could be in. q’ 0 = -closure(q 0) F’ = {q’ Q’ | q’ F } ’(q’, a) = -closure(move(q’, a)) m DFA M has a state ERR Q’ = P(Q) q serves as the “error” state, when needed q ’(ERR, a) = ERR, a By definition of ’ 55

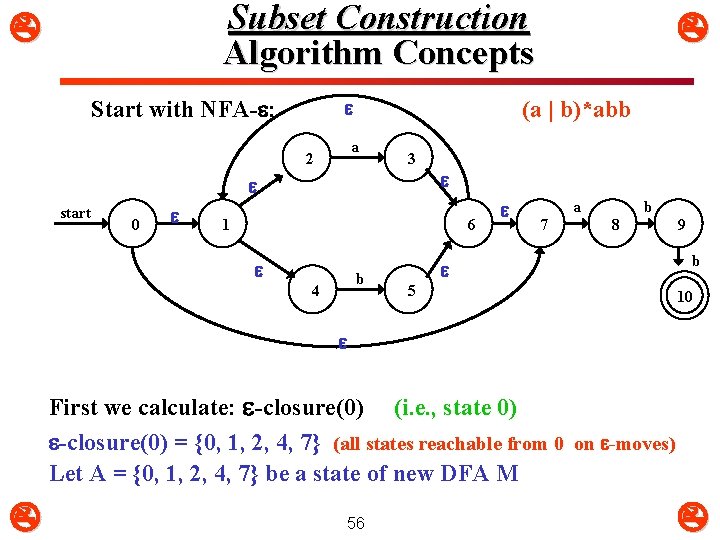
Subset Construction Algorithm Concepts Start with NFA- : (a | b)*abb a 2 3 start 0 1 6 b 4 a 7 b 8 9 b 5 10 First we calculate: -closure(0) (i. e. , state 0) -closure(0) = {0, 1, 2, 4, 7} (all states reachable from 0 on -moves) Let A = {0, 1, 2, 4, 7} be a state of new DFA M 56

Conversion Example (1) 2 nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) a : -closure(move(A, a)) = -closure(move({0, 1, 2, 4, 7}, a))} adds {3, 8} (since move(2, a) = 3 and move(7, a) = 8) From this we have : -closure({3, 8}) = {1, 2, 3, 4, 6, 7, 8} (since 3 6 1 4, 6 7, and 1 2 all by -moves) Let B = {1, 2, 3, 4, 6, 7, 8} be a new state in D. Define M(A, a) = B b : -closure(move(A, b)) = -closure(move({0, 1, 2, 4, 7}, b)) adds {5} (since move(4, b) = 5) From this we have : -closure({5}) = {1, 2, 4, 5, 6, 7} (since 5 6 1 4, 6 7, and 1 2 all by -moves) Let C = {1, 2, 4, 5, 6, 7} be a new state in D. Define M(A, b) = C 57

Conversion Example (2) 3 rd, we calculate for state B on {a, b} a : -closure(move(B, a)) = -closure(move({1, 2, 3, 4, 6, 7, 8}, a))} = {1, 2, 3, 4, 6, 7, 8} = B Define M(B, a) = B b : -closure(move(B, b)) = -closure(move({1, 2, 3, 4, 6, 7, 8}, b))} = {1, 2, 4, 5, 6, 7, 9} = D Define M(B, b) = D 4 th, we calculate for state C on {a, b} a : -closure(move(C, a)) = -closure(move({1, 2, 4, 5, 6, 7}, a))} = {1, 2, 3, 4, 6, 7, 8} = B Define M(C, a) = B b : -closure(move(C, b)) = -closure(move({1, 2, 4, 5, 6, 7}, b))} = {1, 2, 4, 5, 6, 7} = C Define M(C, b) = C 58

Conversion Example (3) 5 th , we calculate for state D on {a, b} a : -closure(move(D, a)) = -closure(move({1, 2, 4, 5, 6, 7, 9}, a))} = {1, 2, 3, 4, 6, 7, 8} = B Define M(D, a) = B b : -closure(move(D, b)) = -closure(move({1, 2, 4, 5, 6, 7, 9}, b))} = {1, 2, 4, 5, 6, 7, 10} = E Define M(D, b) = E Finally, we calculate for state E on {a, b} a : -closure(move(E, a)) = -closure(move({1, 2, 4, 5, 6, 7, 10}, a))} = {1, 2, 3, 4, 6, 7, 8} = B Define M(E, a) = B b : -closure(move(E, b)) = -closure(move({1, 2, 4, 5, 6, 7, 10}, b))} = {1, 2, 4, 5, 6, 7} = C Define M(E, b) = C 59

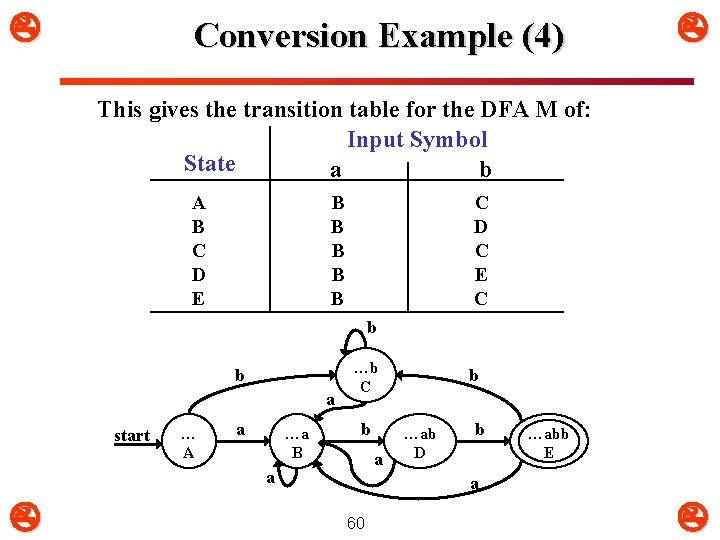
Conversion Example (4) This gives the transition table for the DFA M of: Input Symbol State a b A B C D E B B B C D C E C b b a start … A a …a B …b C b a a b …ab D b …abb E a 60

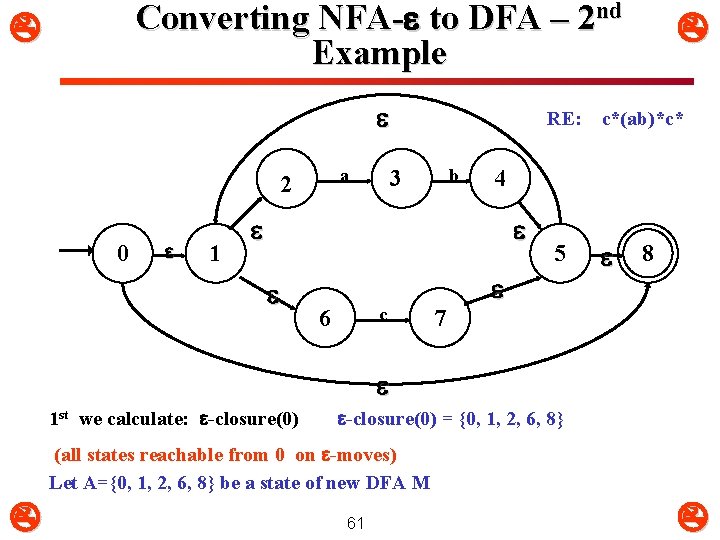
Converting NFA- to DFA – 2 nd Example a 2 0 1 RE: b 3 c 6 7 c*(ab)*c* 4 5 8 1 st we calculate: -closure(0) = {0, 1, 2, 6, 8} (all states reachable from 0 on -moves) Let A={0, 1, 2, 6, 8} be a state of new DFA M 61

Conversion Example (1) 2 nd , we calculate : a : -closure(move(A, a)) and b : -closure(move(A, b)) c : -closure(move(A, c)) a : -closure(move(A, a)) = -closure(move({0, 1, 2, 6, 8}, a))} adds {3} (since move(2, a) = 3) From this we have : -closure({3}) = {3} (since 3 3 by -moves) Let B = {3} be a new state. Define M(A, a) = B b : -closure(move(A, b)) = -closure(move({0, 1, 2, 6, 8}, b)) There is NO transition on b for all states 0, 1, 2, 6 and 8 Define M(A, b) = Reject c : -closure(move(A, c)) = -closure(move({0, 1, 2, 6, 8}, c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1, 2, 5, 6, 7, 8} (since 7 5 8, 7 5 1 2, and 7 5 1 6 by -moves) Let C = {1, 2, 5, 6, 7, 8} be a new state. Define M(A, c) = C 62

Conversion Example (2) 3 rd , we calculate : a : -closure(move(B, a)) and b : -closure(move(B, b)) c : -closure(move(B, c)) a : -closure(move(B, a)) = -cclosure(move({3}, a))} There is NO transition on a for state 3 Define M(B, a) = Reject b : -closure(move(B, b)) = -closure(move({3}, b)) adds {4} (since move(3, b) = 4) From this we have : -closure({4}) = {1, 2, 4, 5, 6, 8} (since 4 5 8, 4 5 1 2, and 4 5 1 6 by -moves) Let D = {1, 2, 4, 5, 6, 8} be a new state. Define M(B, b) = D c : -closure(move(B, c)) = -closure(move({3}, c)) There is NO transition on c for state 3 Define M(B, c) = Reject 63

Conversion Example (3) 4 th , we calculate : a : -closure(move(C, a)) and b : -closure(move(C, b)) c : -closure(move(C, c)) a : -cclosure(move(C, a)) = -closure(move({1, 2, 5, 6, 7, 8}, a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(C, a) = B b : -closure(move(C, b)) = -closure(move({1, 2, 5, 6, 7, 8}, b)) There is NO transition on b for all states 1, 2, 5, 6, and 7 Define M(C, b) = Reject c : -closure(move(C, c)) = -closure(move({1, 2, 5, 6, 7, 8}, c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1, 2, 5, 6, 7, 8} (since 7 5 8, 7 5 1 2, and 7 5 1 6 by -moves) Define M(C, c) = C 64

Conversion Example (4) 5 th , we calculate : a : -closure(move(D, a)) and b : -closure(move(D, b)) c : -closure(move(D, c)) a : -closure(move(D, a)) = -closure(move({1, 2, 4, 5, 6, 8}, a))} adds {3} (since move(2, a) = 3) -closure({3}) = {3} Define M(D, a) = B b : -closure(move(D, b)) = -closure(move({1, 2, 4, 5, 6, 8}, b)) There is NO transition on b for all states 1, 2, 4, 5, 6, and 8 Define M(D, b) = Reject c : -closure(move(D, c)) = -closure(move({1, 2, 4, 5, 6, 8}, c)) adds {7} (since move(6, c) = 7) From this we have : -closure({7}) = {1, 2, 5, 6, 7, 8} (since 7 5 8, 7 5 1 2, and 7 5 1 6 by -moves) Define M(D, c) = C 65

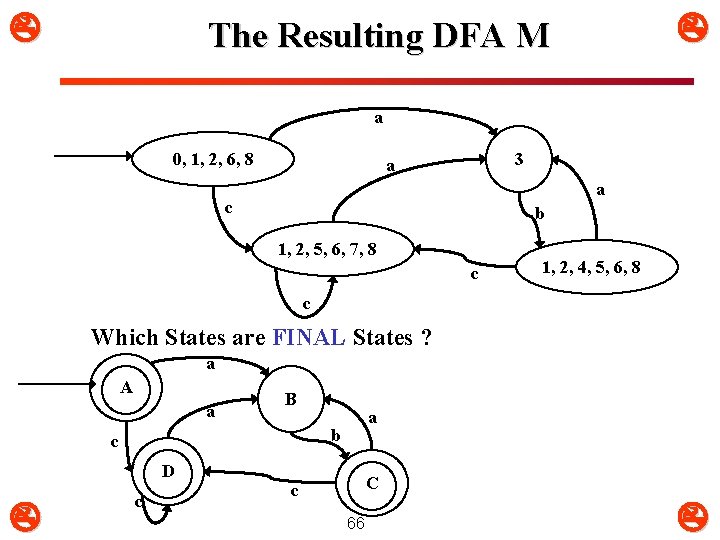
The Resulting DFA M a 0, 1, 2, 6, 8 3 a a c b 1, 2, 5, 6, 7, 8 c 1, 2, 4, 5, 6, 8 c Which States are FINAL States ? a A a B b c D a c C c 66

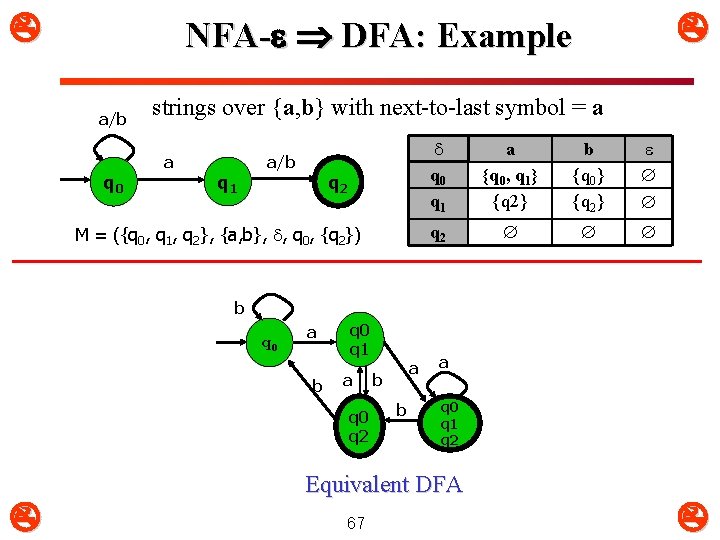
NFA- DFA: Example a/b q 0 strings over {a, b} with next-to-last symbol = a a q 1 a/b q 2 M = ({q 0, q 1, q 2}, {a, b}, , q 0, {q 2}) q 0 q 1 a {q 0, q 1} {q 2} b {q 0} {q 2} q 2 b q 0 a b q 0 q 1 a q 0 q 2 a b b a q 0 q 1 q 2 Equivalent DFA 67

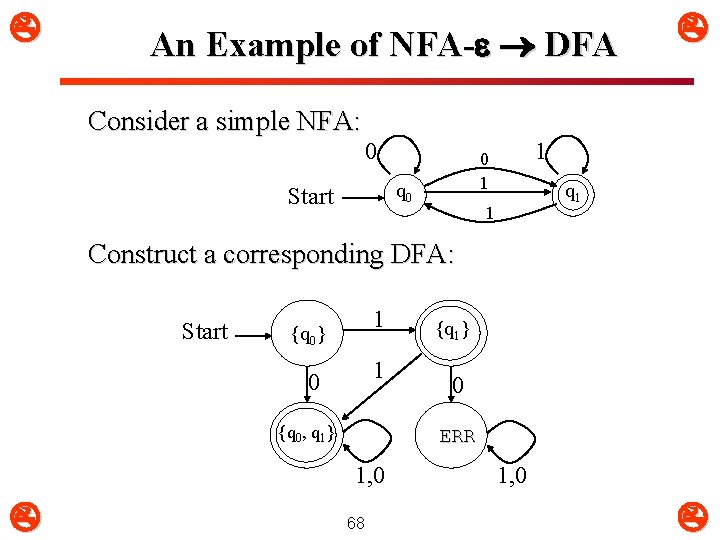
An Example of NFA- DFA Consider a simple NFA: 0 q 0 Start 1 0 1 q 1 1 Construct a corresponding DFA: Start 1 {q 0} 1 0 {q 0, q 1} 0 ERR 1, 0 {q 1} 68 1, 0

Examples m See examples 2. 11, 2. 12, and 2. 13 69

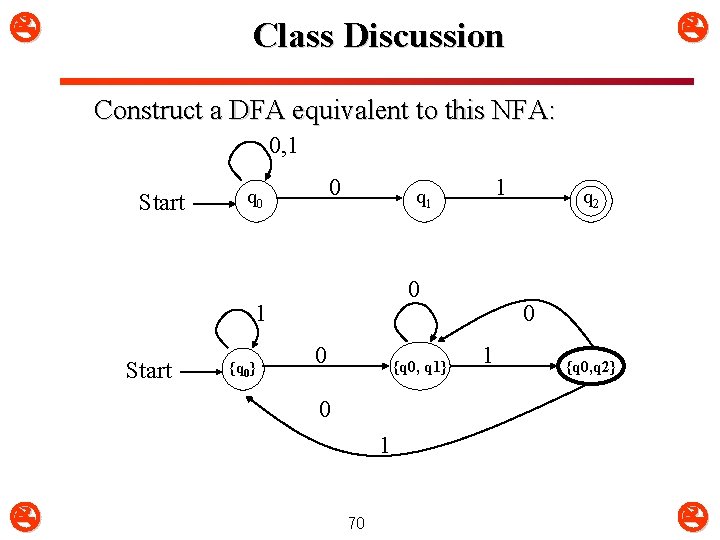
Class Discussion Construct a DFA equivalent to this NFA: 0, 1 Start 0 q 0 0 1 Start {q 0} 1 q 1 0 {q 0, q 1} q 2 0 1 {q 0, q 2} 0 1 70

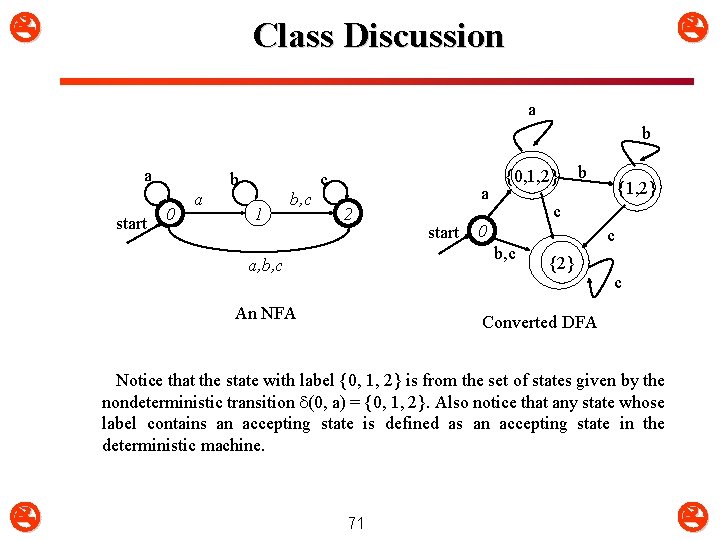
Class Discussion a b a start b 0 a c 1 b, c a 2 start {0, 1, 2} An NFA {1, 2} c 0 b, c a, b, c b c {2} c Converted DFA Notice that the state with label {0, 1, 2} is from the set of states given by the nondeterministic transition (0, a) = {0, 1, 2}. Also notice that any state whose label contains an accepting state is defined as an accepting state in the deterministic machine. 71

2. 4 Reduction of the Number of States in FA m Self study q but not included in the exams material 72