Compiler Construction 2 Lexical Analysis Lexical Analysis Source

Compiler Construction 2주 강의 Lexical Analysis

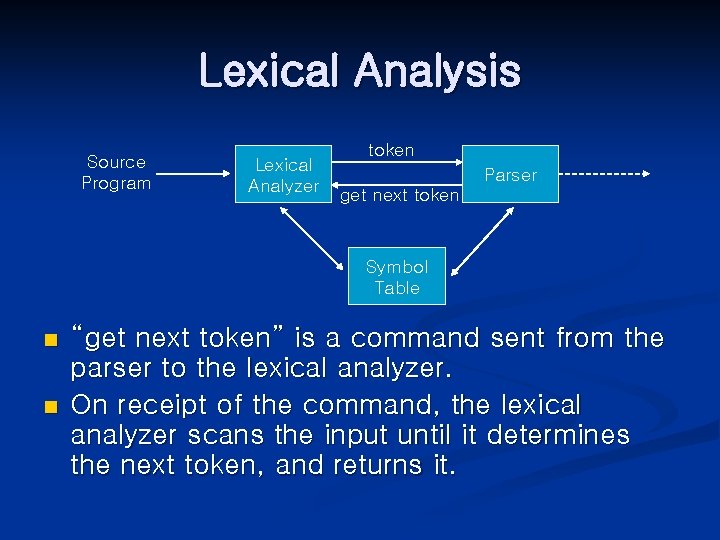
Lexical Analysis Source Program Lexical Analyzer token Parser get next token Symbol Table n n “get next token” is a command sent from the parser to the lexical analyzer. On receipt of the command, the lexical analyzer scans the input until it determines the next token, and returns it.

Other jobs of the lexical analyzer n We also want the lexer to Strip out comments and white space from the source code. n Correlate parser errors with the source code location (the parser doesn’t know what line of the file it’s at, but the lexer does) n

Tokens, patterns, and lexemes n n A TOKEN is a set of strings over the source alphabet. A PATTERN is a rule that describes that set. A LEXEME is a sequence of characters matching that pattern. E. g. in Pascal, for the statement const pi = 3. 1416; n The substring pi is a lexeme for the token identifier

Example tokens, lexemes, patterns Token Sample Lexemes Informal description of pattern if if if While while Relation <, <=, = , <>, > >= < or <= or <> or >= Id count, sun, i, j, pi, D 2 Letter followed by letters and digits Num 0, 12, 3. 1416, 6. 02 E 23 Any numeric constant literal “please enter input values” Any characters between “ and ”

Tokens n n Together, the complete set of tokens form the set of terminal symbols used in the grammar for the parser. In most languages, the tokens fall into these categories: n n n n Keywords Operators Identifiers Constants Literal stirings Punctuation Usually the token is represented as an integer. The lexer and parser just agree on which integers are used for each token.

Token attributes n n If there is more than one lexeme for a token, we have to save additional information about the token. Example: the token number matches lexemes 10 and 20. Code generation needs the actual number, not just the token. With each token, we associate ATTRIBUTES. Normally just a pointer into the symbol table.

Example attributes n For C source code E=M*C*C n We have token/attribute pairs <ID, ptr to symbol table entry for E> <Assign_op, NULL> <ID, ptr to symbol table entry for M> <Mult_op, NULL> <ID, ptr to symbol table entry for C>

Lexical errors n n n When errors occur, we could just crash It is better to print an error message then continue. Possible techniques to continue on error: n n Delete a character Insert a missing character Replace an incorrect character by a correct character Transpose adjacent characters

Token specification n REGULAR EXPRESSIONS (REs) are the most common notation for pattern specification. Every pattern specifies a set of strings, so an RE names a set of strings. Definitions: n n The ALPHABET (often written ∑) is the set of legal input symbols A STRING over some alphabet ∑ is a finite sequence of symbols from ∑ The LENGTH of string s is written |s| The EMPTY STRING is a special 0 -length string denoted ε

More definitions: strings and substrings n n A PREFIX of s is formed by removing 0 or more trailing symbols of s A SUFFIX of s is formed by removing 0 or more leading symbols of s A SUBSTRING of s is formed by deleting a prefix and a suffix from s A PROPER prefix, suffix, or substring is a nonempty string x that is, respectively, a prefix, suffix, or substring of s but with x ≠ s.

More definitions n n A LANGUAGE is a set of strings over a fixed alphabet ∑. Example languages: n n n Ø (the empty set) {ε} { a, aaa, aaaa } The CONCATENATION of two strings x and y is written xy String EXPONENTIATION is written si, where s 0 = ε and si = si-1 s for i>0.

Operations on languages We often want to perform operations on sets of strings (languages). The important ones are: n The UNION of L and M: L ∪ M = { s | s is in L OR s is in M } n The CONCATENATION of L and M: LM = { st | s is in L and t is in M } n The KLEENE CLOSURE of L: n The POSITIVE CLOSURE of L:

Regular expressions REs let us precisely define a set of strings. n For C identifiers, we might use ( letter | _ ) ( letter | digit | _ )* n Parentheses are for grouping, | means “OR”, and * means Kleene closure. n Every RE defines a language L(r). n

Regular expressions n Here are the rules for writing REs over an alphabet ∑ : 1. 2. 3. ε is an RE denoting { ε }, the language containing only the empty string. If a is in ∑, then a is a RE denoting { a }. If r and s are REs denoting L(r) and L(s), then 1. 2. 3. 4. (r)|(s) is a RE denoting L(r) ∪ L(s) (r)(s) is a RE denoting L(r) L(s) (r)* is a RE denoting (L(r))* (r) is a RE denoting L(r)

Additional conventions n To avoid too many parentheses, we assume: 1. 2. 3. * has the highest precedence, and is left associative. Concatenation has the 2 nd highest precedence, and is left associative. | has the lowest precedence and is left associative.

Example REs 1. 2. 3. 4. 5. a|b (a|b) a* (a | b )* a | a*b

Equivalence of REs Axiom Description r|s = s|r | is commutative r|(s|t) = (r|s)t | is associative (rs)t = r(st) Concatenation is associative r(s|t) = rs|rt (s|t)r = sr|tr Concatenation distributes over | εr=r rε=r ε Is the identity element for concatenation r* = (r| ε)* Relation between r** = r* * is idempotent * and ε

Regular definitions n To make our REs simpler, we can give names to subexpressions. A REGULAR DEFINITION is a sequence d 1 -> r 1 d 2 -> r 2 … dn -> rn

Regular definitions n Example for identifiers in C: letter -> A | B | … | Z | a | b | … | z digit -> 0 | 1 | … | 9 id -> ( letter | _ ) ( letter | digit | _ )* n Example for numbers in Pascal: digit -> 0 | 1 | … | 9 digits -> digit* optional_fraction ->. digits | ε optional_exponent -> ( E ( + | - | ε ) digits ) | ε num -> digits optional_fraction optional_exponent

Notational shorthand n To simplify out REs, we can use a few shortcuts: n n 1. + means “one or more instances of” a+ (ab)+ 2. ? means “zero or one instance of” Optional_fraction -> (. digits ) ? 3. [] creates a character class [A-Za-z][A-Za-z 0 -9]* You can prove that these shortcuts do not increase the representational power of REs, but they are convenient.

Token recognition n We now know how to specify the tokens for our language. But how do we write a program to recognize them? if then else relop id num -> -> -> if then else < | <= | <> | >= letter ( letter | digit )* digit (. digit )? ( E (+|-)? digit )?

Token recognition n We also want to strip whitespace, so we need definitions delim ws -> -> blank | tab | newline delim+

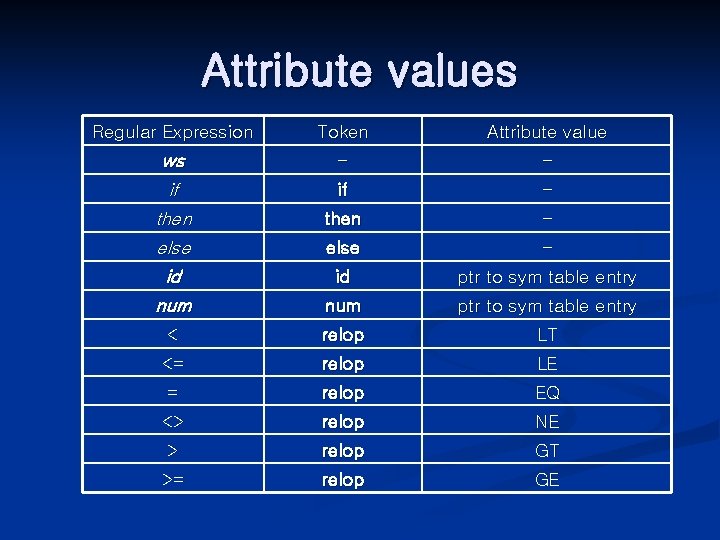
Attribute values Regular Expression Token Attribute value ws if - - if - then else then - else - id num id ptr to sym table entry num ptr to sym table entry < relop LT <= relop LE = relop EQ <> relop NE > relop GT >= relop GE

Transition diagrams n n n n Transition diagrams are also called finite automata. We have a collection of STATES drawn as nodes in a graph. TRANSITIONS between states are represented by directed edges in the graph. Each transition leaving a state s is labeled with a set of input characters that can occur after state s. For now, the transitions must be DETERMINISTIC. Each transition diagram has a single START state and a set of TERMINAL STATES. The label OTHER on an edge indicates all possible inputs not handled by the other transitions. Usually, when we recognize OTHER, we need to put it back in the source stream since it is part of the next token. This action is denoted with a * next to the corresponding state.

Automated lexical analyzer generation n Next time we discuss Lex and how it does its job: n Given a set of regular expressions, produce C code to recognize the tokens.

Lexical Analysis

Lexical Analysis Example

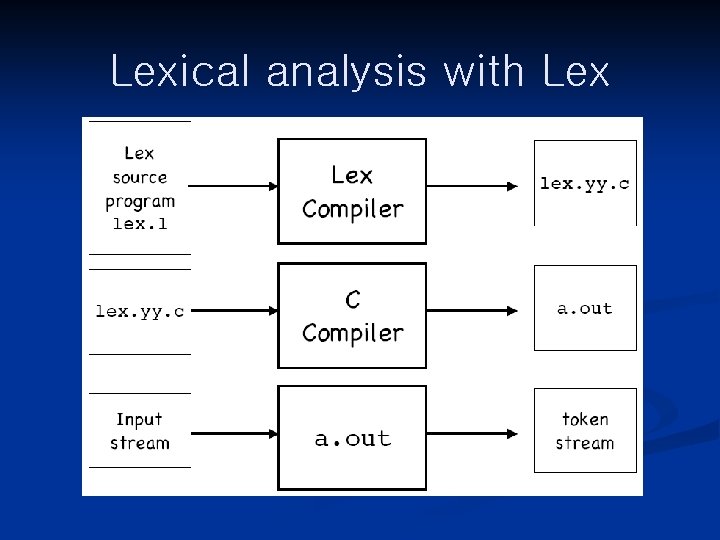
Lexical Analysis With Lex

Lexical analysis with Lex

Lex source program format n The Lex program has three sections, separated by %%: declarations %% transition rules %% auxiliary code

Declarations section n n Code between %{ and }% is inserted directly into the lex. yy. c. Should contain: n Manifest constants (#define for each token) n Global variables, function declarations, typedefs Outside %{ and }%, REGULAR DEFINITIONS are declared. Examples: delim ws letter [ tn] {delim}+ [A-Za-z] Each definition is a name followed by a pattern. Declared names can be used in later patterns, if surrounded by { }.

Translation rules section Translation rules take the form p 1 { action 1 } p 2 { action 2 } …… pn { actionn } Where pi is a regular expression and actioni is a C program fragment to be executed whenever pi is recognized in the input stream. In regular expressions, references to regular definitions must be enclosed in {} to distinguish them from the corresponding character sequences.

Auxiliary procedures n Arbitrary C code can be placed in this section, e. g. functions to manipulate the symbol table. n 이미 설명했음

Special characters Some characters have special meaning to Lex. n ‘. ’ in a RE stands for ANY character n ‘*’ stands for Kleene closure n ‘+’ stands for positive closure n ‘? ’ stands for 0 -or-1 instance of n ‘-’ produces a character range (e. g. in [A-Z]) When you want to use these characters in a RE, they must be “escaped” e. g. in RE {digit}+(. {digit}+)? ‘. ’ is escaped with ‘’

Lex interface to yacc n n The yacc parser calls a function yylex() produced by lex. yylex() returns the next token it finds in the input stream. yacc expects the token’s attribute, if any, to be returned via the global variable yylval. The declaration of yylval is up to you (the compiler writer). In our example, we use a union, since we have a few different kinds of attributes.

Lookahead in Lex Sometimes, we don’t know until looking ahead several characters what the next token is. Recognition of the DO keyword in Fortran is a famous example. DO 5 I=1. 25 assigns the value 1. 25 to DO 5 I=1, 25 is a DO loop Lex handles long-term lookahead with r 1/r 2: DO/({letter}|{digit})*=({letter}|{digit})*, Recognize keyword DO (if it’s followed by letters & digits, ‘=’, more letters & digits, followed by a ‘, ’)

Finite Automata for Lexical Analysis

Automatic lexical analyzer generation n How do Lex and similar tools do their job? n Lex translates regular expressions into transition diagrams. n Then it translates the transition diagrams into C code to recognize tokens in the input stream. n There are many possible algorithms. n The simplest algorithm is RE -> NFA -> DFA -> C code.

Finite automata (FAs) and regular languages n n n A RECOGNIZER takes language L and string x as input, and responds YES if x∈L, or NO otherwise. The finite automaton (FA) is one class of recognizer. A FA is DETERMINISTIC if there is only one possible transition for each <state, input> pair. A FA is NONDETERMINISTIC if there is more than one possible transition some <state, input> pair. BUT both DFAs and NFAs recognize the same class of languages: REGULAR languages, or the class of languages that can be written as regular expressions.

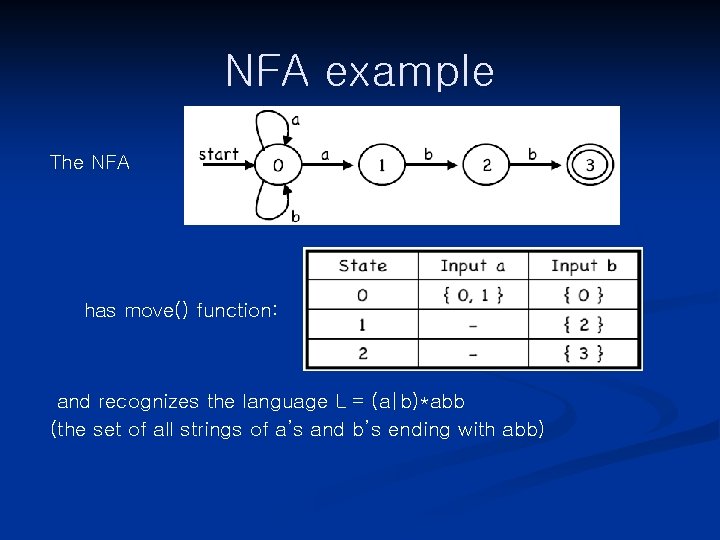
NFAs n A NFA is a 5 -tuple < S, ∑, move, s 0, F > n S is the set of STATES in the automaton. ∑ is the INPUT CHARACTER SET move( s, c ) = S is the TRANSITION FUNCTION specifying which states S the automaton can move to on seeing input c while in state s. s 0 is the START STATE. F is the set of FINAL, or ACCEPTING STATES n n

NFA example The NFA has move() function: and recognizes the language L = (a|b)*abb (the set of all strings of a’s and b’s ending with abb)

The language defined by a NFA n An NFA ACCEPTS string x iff there exists a path from s 0 to an accepting state, such that the edge labels along the path spell out x. n The LANGUAGE DEFINED BY a NFA N, written L(N), is the set of strings it accepts.

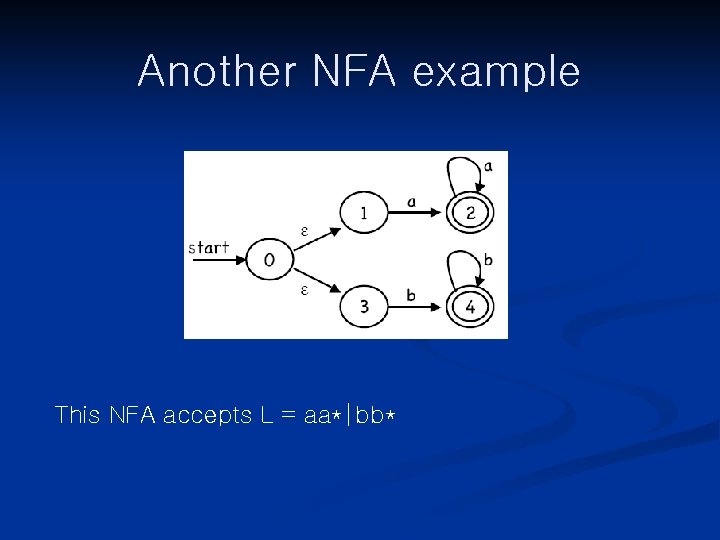
Another NFA example This NFA accepts L = aa*|bb*

Deterministic FAs (DFAs) The DFA is a special case of the NFA except: n No state has an ε-transition n No state has more than one edge leaving it for the same input character. The benefit of DFAs is that they are simple to simulate: there is only one choice for the machine’s state after each input symbol.

Algorithm to simulate a DFA Inputs: Outputs: Method: string x terminated by EOF; DFA D = < S, ∑, move, s 0, F > YES if D accepts x; NO otherwise s = s 0 ; c = nextchar; while ( c != EOF ) { s = move( s, c ); c = nextchar; } if ( s ∈ F ) return YES else return NO

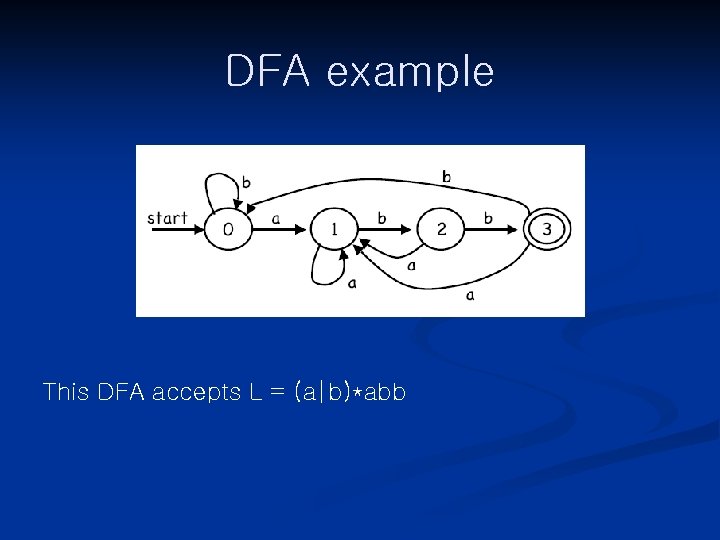
DFA example This DFA accepts L = (a|b)*abb

RE -> DFA n n Now we know how to simulate DFAs. If we can convert our REs into a DFA, we can automatically generate lexical analyzers. BUT it is not easy to convert REs directly into a DFA. Instead, we will convert our REs to a NFA then convert the NFA to a DFA.

Converting a NFA to a DFA

NFA -> DFA n n n NFAs are ambiguous: we don’t know what state a NFA is in after observing each input. The simplest conversion method is to have the DFA track the SUBSET of states the NFA MIGHT be in. We need three functions for the construction: n ε-closure(s): the set of NFA states reachable from NFA state s on ε-transitions alone. n ε-closure(T): the set of NFA states reachable from some state s ∈ T on ε-transitions alone. n move(T, a): the set of NFA states to which there is a transition on input a from some NFA state s ∈ T

Subset construction algorithm n n n Inputs: Outputs: Method: a NFA N = < SN, ∑, tran. N, n 0, FN > a DFA D = < SD, ∑, tran. D, d 0, FD > add a state d 0 to SD corresponding to ε-closure(n 0) while there is an unexpanded state di ∈ SD { for each input symbol a ∈ ∑ { dj = ε-closure(move(di, a)) if dj ∉ SD, add dj to SD tran. N( di, a ) = dj } }

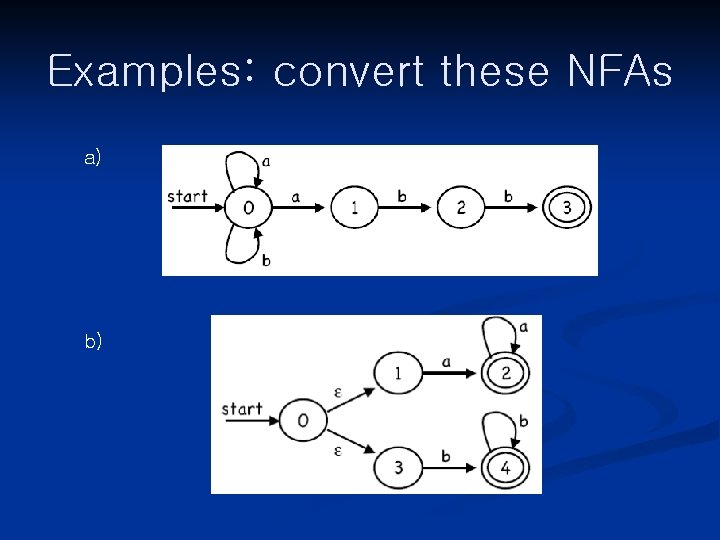
Examples: convert these NFAs a) b)

Converting a RE to a NFA

RE -> NFA n n n The construction is bottom up. Construct NFAs to recognize ε and each element a ∈ ∑. Recursively expand those NFAs for alternation, concatenation, and Kleene closure. Every step introduces at most two additional NFA states. Therefore the NFA is at most twice as large as the regular expression.

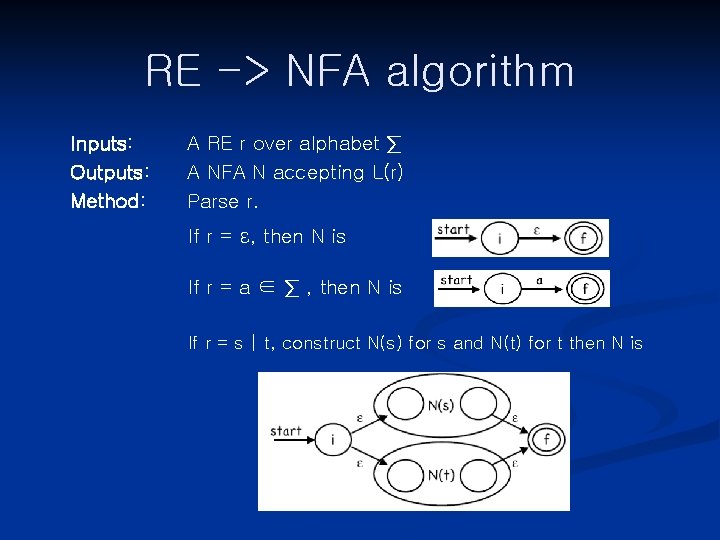
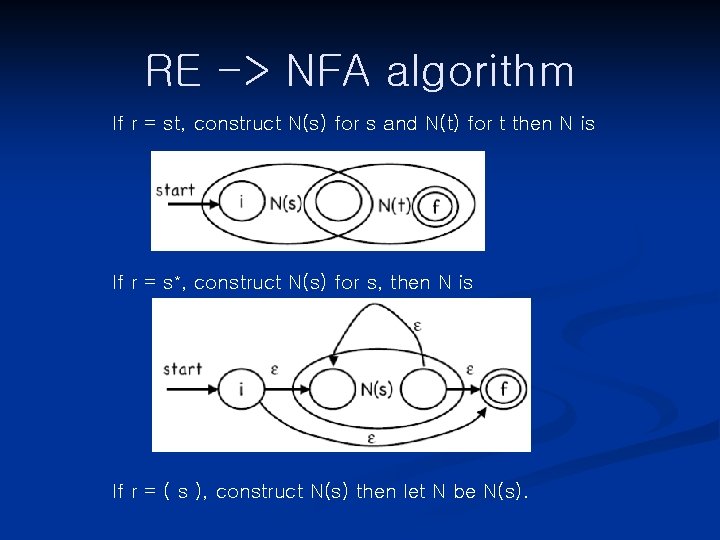
RE -> NFA algorithm Inputs: Outputs: Method: A RE r over alphabet ∑ A NFA N accepting L(r) Parse r. If r = ε, then N is If r = a ∈ ∑ , then N is If r = s | t, construct N(s) for s and N(t) for t then N is

RE -> NFA algorithm If r = st, construct N(s) for s and N(t) for t then N is If r = s*, construct N(s) for s, then N is If r = ( s ), construct N(s) then let N be N(s).

Example Use the NFA construction algorithm to build a NFA for r = (a|b)*abb