Chapter 9 Reasoning in Uncertain Situations Contents Uncertain

Chapter 9 Reasoning in Uncertain Situations Contents Uncertain situations Non-monotonic logic and reasoning Certainty Factor algebra Fuzzy logic and reasoning Dempster-Shafer theory of evidence Bayesian belief network Markov models CSC 411 Artificial Intelligence 1

Traditional Logic Based on predicate logic Three important assumptions: – Predicate descriptions are sufficient w. r. t. to the domain – Information is consistent – Knowledge base grows monotonically CSC 411 Artificial Intelligence 2

Non-monotonic Logic Addresses the three assumptions of traditional logic – Knowledge is incomplete No knowledge about p: true or false? Prolog – closed world assumption – Knowledge is inconsistent Based on how the world usually works Most birds fly, but Ostrich doesn’t – Knowledge base grows non-monotonically New observation may contradict the existing knowledge, thus the existing knowledge may need removal. Inference based on assumptions, how come if the assumptions are later shown to be incorrect Three modal operators are introduced CSC 411 Artificial Intelligence 3

Unless Operator New information may invalidate previous results Implemented in TMS – Truth Maintenance Systems to keep track of the reasoning steps and preserve the KB consistency Introduce Unless operator – Support inferences based on the belief that its argument is not true – Consider p(X) unless q(X) r(X) If p(X) is true and not believe q(X) true then r(X) p(Z) r(W) s(W) From above, conclude s(X). Later, change believe or find q(X) true, what happens? Retract r(X) and s(X) – Unless deals with believe, not truth Either unknown or believed false Believed or known true – Monotonocity CSC 411 Artificial Intelligence 4

Is-consistent-with Operator M When reason, make sure the premises are consistent Format: M p – p is consistent with KB Consider – X good_student(X) M study_hard(X) graduates(X) – For all X who is a good student, if the fact that X studies hard is consistent with KB, then X will graduate – Not necessary to prove that X study hard. How to decide p is consistent with KB – Negation as failure – Heuristic-based and limited search CSC 411 Artificial Intelligence 5

Default Logic Introduce a new format of inference rules: – A(Z) : B(Z) C(Z) – If A(Z) is provable, and it is consistent with what we know to assume B(Z), then conclude C(Z) Compare with is-consistent-with operator – Similar – Difference is the reasoning method In default logic, new rules are used to infer sets of plausible extensions – Example: X good_student(X) : study_hard(X) graduates(X) Y party(Y) : not(study_hard(Y)) not(graduates(X)) CSC 411 Artificial Intelligence 6

Stanford Certainty Factor Algebra Measure of confidence or believe Summation may not be 1 Simple case: – Confidence for: MB(H|E) – Confidence against: MD(H|E) – Properties: 1>MB(H|E)>0 while MD(H|E)=0, or 1>MD(H|E)>0 while MB(H|E)=0 – Put together CF(H|E) = MB(H|E) – MD(H|E) 1 > CF(H|E) > -1 CSC 411 Artificial Intelligence 7

CF Combination Premises combination – CF( P and Q) = min(CF(P), CF(Q)) – CF( P or Q) = max(CF(P), CF(Q)) Rule CF: each rule has a confidence measure CF propagation – Rule R: P Q with CF=CF(R) – CF(Q) = CF(P) CF(R) Rule combination – – – CSC 411 Rules R 1: P 1 Q: CF 1(Q) = CF(P 1)x. CF(R 1) R 2: P 2 Q: CF 2(Q) = CF(P 2)x. CF(R 2) CF(Q) = CF 1+CF 2 – (CF 1 x. CF 2) if both positive CF 1+CF 2 + (CF 1 x. CF 2) if both negative (CF 1+CF 2)/(1 -min(|CF 1|, |CF 2|)) otherwise Artificial Intelligence 8

Fuzzy Sets Classic sets – Completeness: x in either A or ¬A – Exclusive: can not be in both A and ¬A Fuzzy sets – Violate the two assumptions – Possibility theory -- measure of confidence or believe – Probability theory – randomness – Process imprecision – Introduce membership function – Believe x A in some degree between 0 and 1, inclusive CSC 411 Artificial Intelligence 9

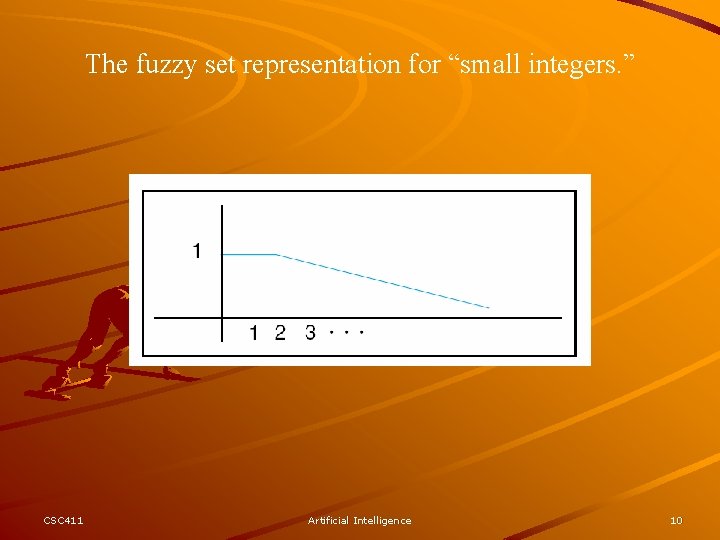
The fuzzy set representation for “small integers. ” CSC 411 Artificial Intelligence 10

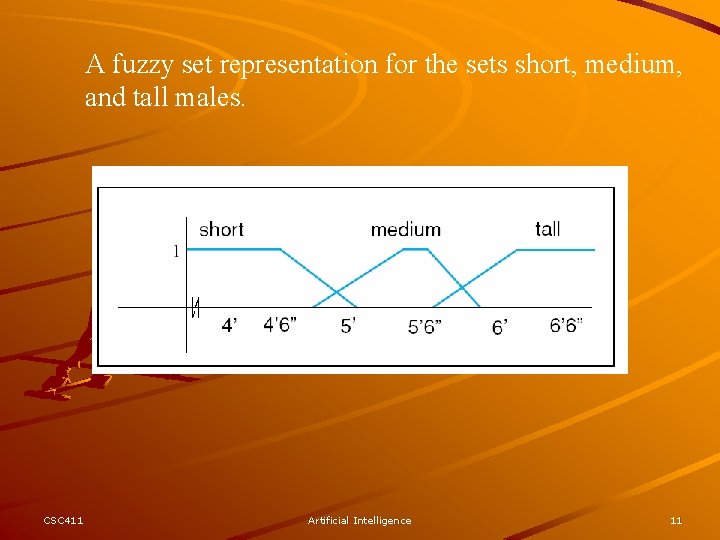
A fuzzy set representation for the sets short, medium, and tall males. CSC 411 Artificial Intelligence 11

Fuzzy Set Operations Fuzzy set operations are defined as the operations of membership functions Complement: ¬A = C – m. C = 1 – m. A Union: A B =C – m. C = max(m. A, m. B) Intersection: A B = C – m. C = min(m. A, m. B) Difference: A – B = C – m. C = max(0, m. A-m. B) CSC 411 Artificial Intelligence 12

Fuzzy Inference Rules Rule format and computation – If x is A and y is B then z is C m. C(z) = min(m. A(x), m. B(y)) – If x is A or y is B then z is C m. C(z) = max(m. A(x), m. B(y)) – If x is not A then z is C m. C(z) = 1 – m. A(x) CSC 411 Artificial Intelligence 13

The inverted pendulum and the angle θ and dθ/dt input values. CSC 411 Artificial Intelligence 14

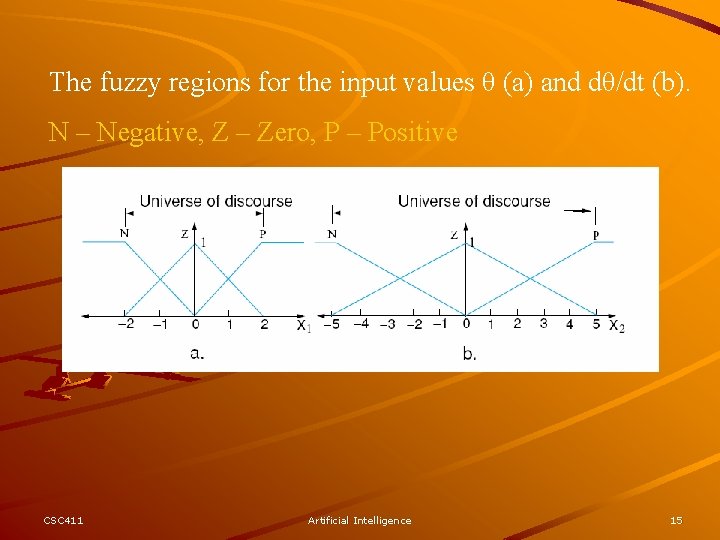
The fuzzy regions for the input values θ (a) and dθ/dt (b). N – Negative, Z – Zero, P – Positive CSC 411 Artificial Intelligence 15

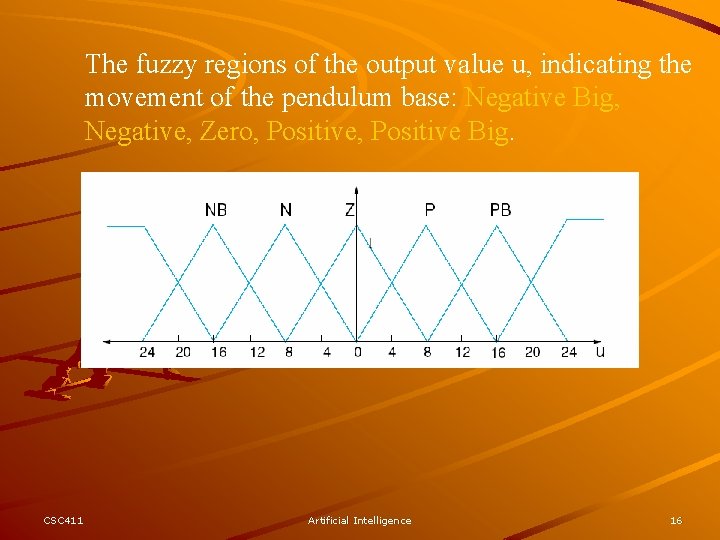
The fuzzy regions of the output value u, indicating the movement of the pendulum base: Negative Big, Negative, Zero, Positive Big. CSC 411 Artificial Intelligence 16

The fuzzificzation of the input measures X 1 = 1: m. Z(X 1) = m. P(X 1) = 0. 5, m. N(X 1) = 0 X 2 = -4: m. Z(X 2) = 0. 2, m. N(X 2) = 0. 8 , m. P(X 2) = 0 CSC 411 Artificial Intelligence 17

The Fuzzy Associative Matrix (FAM) for the pendulum problem. The input values are on the left and top. Fuzzy Rules: CSC 411 Artificial Intelligence 18

The fuzzy consequents (a) and their union (b). The centroid of the union (-2) is the crisp output. CSC 411 Artificial Intelligence 19

Dempster-Shafer Theory Probability theory limitation – Assign a single number to measure any situation, no matter how it is complex – Cannot deal with missing evidence, heuristics, and limited knowledge Dempster-Shafer theory – Extend probability theory – Consider a set of propositions as a whole – Assign a set of propositions an interval [believe, plausibility] to constraint the degree of belief for each individual propositions in the set – The belief measure bel is in [0, 1] 0 – no support evidence for a set of propositions 1 – full support evidence for a set of propositions – The plausibility of p, pl(p) = 1 – bel(not(p)) Reflect how evidence of not(p) relates to the possibility for belief in p Bel(not(p))=1: full support for not(p), no possibility for p Bel(not(p))=0: no support for not(p), full possibility for p Range is also in [0, 1] CSC 411 Artificial Intelligence 20

Properties of Dempster-Shafer Initially, no support evidence for either competing hypotheses, say h 1 and h 2 – Dempster-Shafer: [bel, pl] = [0, 1] – Probability theory: p(h 1)=p(h 2)=0. 5 Dempster-Shafer belief functions satisfy weaker axioms than probability function Two fundamental ideas: – Obtaining belief degrees for one question from subjective probabilities for related questions – Using Dempster rule to combine these belief degrees when they are based on independent evidence CSC 411 Artificial Intelligence 21

An Example Two persons M and B with reliabilities detect a computer and claim the result independently. How you believe their claims? Question (Q): detection claim Related question (RQ): detectors’ reliability Dempster-Shafer approach – Obtain belief degrees for Q from subjective (prior) probabilities for RQ for each person – Combine belief degrees from two persons Person M: – – reliability 0. 9, unreliability 0. 1 Claim h 1 Belief degree of h 1 is bel(h 1)=0. 9 Belief degree of not(h 1) is bel(not(h 1))=0. 0, different from probability theory, since no evidence supporting not(h 1) – pl(h 1) = 1 – bel(not(h 1)) = 1 -0 =1 – Thus belief measure for M claim h 1 is [0. 9, 1] Person B: – – CSC 411 Reliability 0. 8, unreliability 0. 2 Claim h 2 bel(h 2) =0. 8, bel(not(h 2))=0, pl(h 2)=1 -bel(not(h 2))=1 -0 Belief measure for B claim h 2 is [0. 8, 1] Artificial Intelligence 22

Combining Belief Measure Set of propositions: M claim h 1 and B claim h 2 – Case 1: h 1 = h 2 Reliability M and B: 09 x 0. 8=0. 72 Unreliability M and B: 0. 1 x 0. 2=0. 02 The probability that at least one of two is reliable: 1 -0. 02=0. 98 Belief measure for h 1=h 2 is [0. 98, 1] – Case 2: h 1 = not(h 2) Cannot be both correct and reliable At least one is unreliable – – Reliable M and unreliable B: 0. 9 x(1 -0. 8)=0. 18 Reliable B and unreliable M: 0. 8 x(1 -0. 1)=0. 08 Unreliable M and B: (1 -0. 9)x(1 -0. 8)=0. 02 At least one is unreliable: 0. 18+0. 02=0. 28 Given at least one is unreliable, posterior probabilities – Reliable M and unreliable B: 0. 18/0. 28=0. 643 – Reliable B and unreliable M: 0. 08/0. 28=0. 286 Belief measure for h 1 – – – Bel(h 1)=0. 643, bel(not(h 1))=bel(h 2)=0. 286 Pl(h 1)=1 -bel(not(h 1))=1 -0. 286=0. 714 Belief measure: [0. 643, 0. 714] Belief measure for h 2 – Bel(h 2)=0. 286, bel(not(h 2))=bel(h 1)=0. 683 – Pl(h 2)=1 -bel(not(h 2))=1 -0. 683=0. 317 – Belief measure: [0. 286, 0. 317] CSC 411 Artificial Intelligence 23

Dempster’s Rule Assumption: – – probable questions are independent a priori As new evidence collected and conflicts, independency may disappear Two steps 1. Sort the uncertainties into a priori independent pieces of evidence 2. Carry out Dempster rule Consider the previous example – – After M and B claimed, a repair person is called to check the computer, and both M and B witnessed this. Three independent items of evidence must be combined Not all evidence is directly supportive of individual elements of a set of hypotheses, but often supports different subsets of hypotheses, in favor of some and against others CSC 411 Artificial Intelligence 24

General Dempster’s Rule Q – an exhaustive set of mutually exclusive hypotheses Z – a subset of Q M – probability density function to assign a belief measure to Z Mn(Z) – belief degree to Z, where n is the number of sources of evidences CSC 411 Artificial Intelligence 25

Bayesian Belief Network A computational model for reasoning to the best explanation of a data set in the uncertainty context Motivation – Reduce the number of parameters of the full Bayesian model – Show the data can partition and focus reasoning – Avoid use of a large joint probability table to compute probabilities for all possible events combination Assumption – Events are either conditionally independent or their correlations are so small that they can be ignored Directed Graphical Model – The events and (cause-effect) relationships form a directed graph, where events are vertices and relationships are links CSC 411 Artificial Intelligence 26

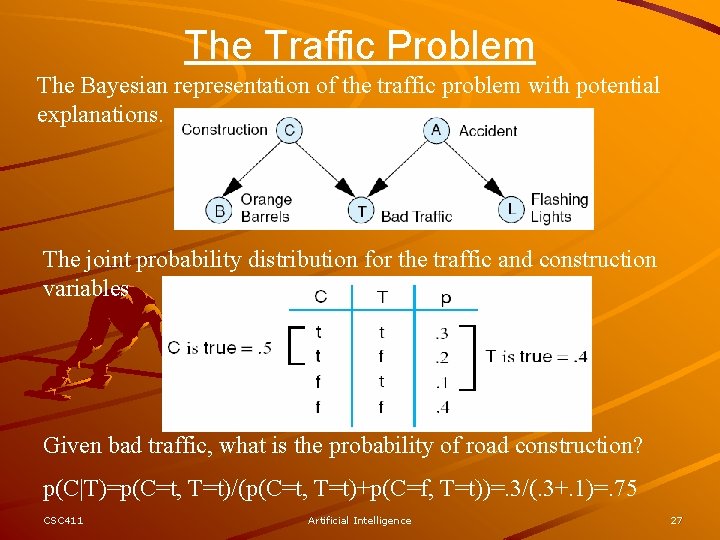
The Traffic Problem The Bayesian representation of the traffic problem with potential explanations. The joint probability distribution for the traffic and construction variables Given bad traffic, what is the probability of road construction? p(C|T)=p(C=t, T=t)/(p(C=t, T=t)+p(C=f, T=t))=. 3/(. 3+. 1)=. 75 CSC 411 Artificial Intelligence 27

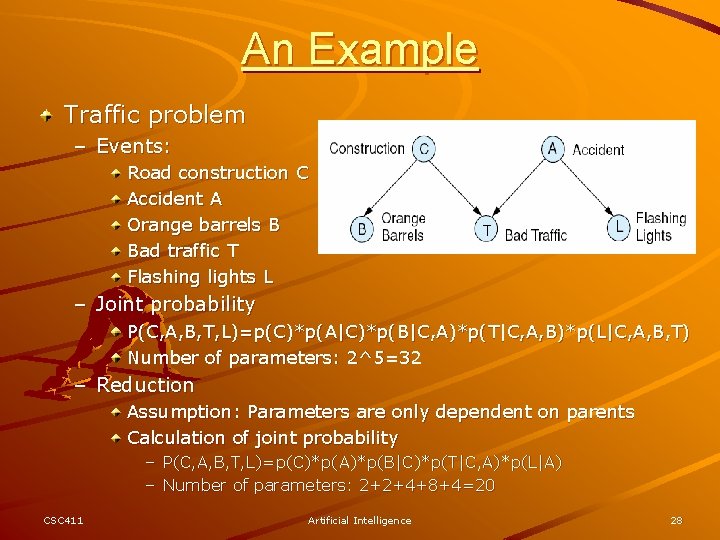
An Example Traffic problem – Events: Road construction C Accident A Orange barrels B Bad traffic T Flashing lights L – Joint probability P(C, A, B, T, L)=p(C)*p(A|C)*p(B|C, A)*p(T|C, A, B)*p(L|C, A, B, T) Number of parameters: 2^5=32 – Reduction Assumption: Parameters are only dependent on parents Calculation of joint probability – P(C, A, B, T, L)=p(C)*p(A)*p(B|C)*p(T|C, A)*p(L|A) – Number of parameters: 2+2+4+8+4=20 CSC 411 Artificial Intelligence 28

BBN Definition Links represent conditional probabilities for causal influence These influences are directed: presence of some event causes other events These influences are not circular Thus a BBN is a DAG: Directed Acyclic Graph CSC 411 Artificial Intelligence 29

Discrete Markov Process Finite state machine – A graphical representation – State transition depends on input stream – States and transitions reflect properties of a formal language Probabilistic finite state machine – A finite state machine – Transition function represented by a probability distribution on the current state Discrete Markov process (chain, machine) – A specialization of probabilistic finite state machine – Ignores its input values CSC 411 Artificial Intelligence 30

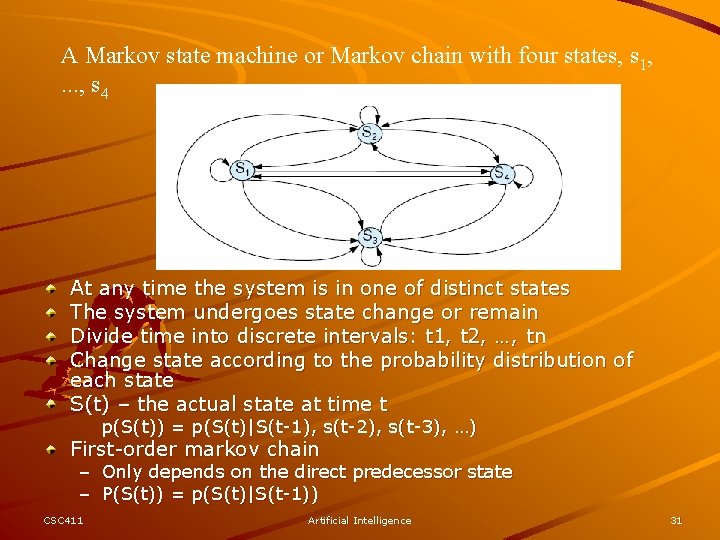
A Markov state machine or Markov chain with four states, s 1, . . . , s 4 At any time the system is in one of distinct states The system undergoes state change or remain Divide time into discrete intervals: t 1, t 2, …, tn Change state according to the probability distribution of each state S(t) – the actual state at time t p(S(t)) = p(S(t)|S(t-1), s(t-2), s(t-3), …) First-order markov chain – Only depends on the direct predecessor state – P(S(t)) = p(S(t)|S(t-1)) CSC 411 Artificial Intelligence 31

Observable Markov Model Assume p(S(t)|S(t-1)) is time invariant, that is, transition between specific states retains the same probabilistic relationship State transition probability aij between si and sj: – aij=p(S(t)=si|S(t-1)=sj), 1<=i, j<=N – If i=j, no transition (remain the same state) – Properties: aij >=0, iaij=1 CSC 411 Artificial Intelligence 32

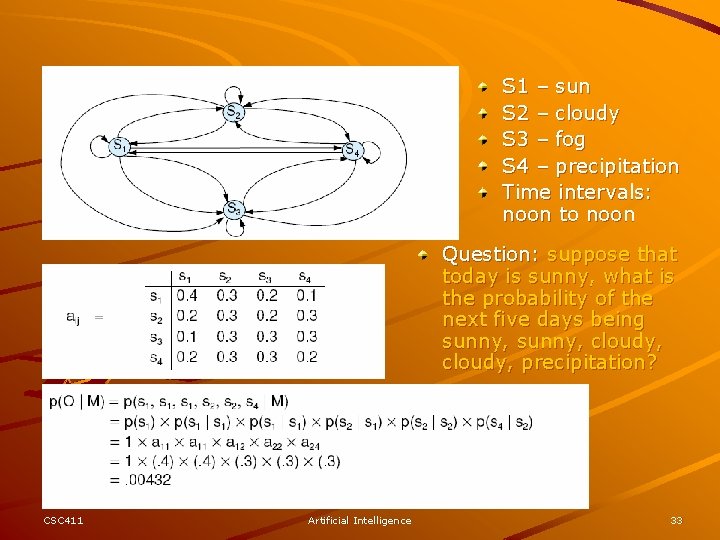
S 1 – sun S 2 – cloudy S 3 – fog S 4 – precipitation Time intervals: noon to noon Question: suppose that today is sunny, what is the probability of the next five days being sunny, cloudy, precipitation? CSC 411 Artificial Intelligence 33