Application of Mathematics in Practical Situations of Life
















- Slides: 16

Application of Mathematics in Practical Situations of Life Presented By: Vardaan Sahgal, Eshan Uniyal, Salman Nehru, Bhavesh Kaushik, Ritvik Kumar, Harshul Siddharth, & Rishabh Mishra From Class VII-F By : Vardaan Sahgal

N O I T A T N E U O Y L L I W N R A LE IN S C I T A S M E E R E P F H I T L IS A F H M NO T F N I O T O I U N T ABO ICATIO SITUA O T L L P E A C N AP CTIC N O I A T R A R E I R P P EF O R R P H T By : I D N W A Vardaan O I T Sahgal A R

By: Vardaan Sahgal Ratio And Proportion Ratio We compare the two quantities in terms of ‘how many times’. This comparison is known as the ratio. We donate ratio using symbol ‘: ’ Eg. 2: 4=2/4=1: 2 Proportion If two ratios are not equal, then we say that they are not in proportion. In a statement of proportion, the four quantities involved when taken in order are known as respective terms. First and fourth terms are known as extreme terms. Second and third terms are known as middle terms. E. g. . 35 : 70 : : 2 : 4; - 35, 70, 2, 4

By: Vardaan Sahgal Example Of Ratio EXAMPLE- Length & breadth of a rectangular field are 50 m & 15 m respectively. Find the ratio of the length to the breadth of the field. SOLUTION : - Length of the rectangular field=50 m Breadth of the rectangular field=15 m The ratio of the length to the breadth is 50: 15 50 50/5 10 The ratio can be written as , --- = ----- =--- = 10 : 3 15 15/5 3 Thus , the required ratio is 10 : 3.

EXAMPLE OF RATIO Example: The area of a rectangular field is 75 m 2 whose length is 10 m. Find the ratio of breadth to the length of this rectangular field. Solution: Length of the rectangular field = 10 m = 10 × 100 cm = 1000 cm Area of the rectangular field = 75 m 2 = 75 × 100 cm 2 = 750000 cm 2 We know that: Area of rectangular field = Length × Breadth Therefore, ratio of breadth to the length of the rectangle By: Thus, the required ratio is 3: 4. Harshul Siddharth

EXAMPLE OF PROPORTION Check whether the following ratios form a proportion. (a) 24 sec: 2 min and 40 cm: 2 m (b) Rs 5: 60 paise and 2 L: 240 ml (c) 60 kg: 1 quintal and 45 min: 1 hour Solution: (a) 24 sec: 2 min = Clearly, 24 sec: 2 min = 40 cm: 2 m Hence, the given ratios form a proportion. (b) Clearly, Rs 5: 60 paise = 2 L: 240 m. L Hence, the given ratios form a proportion. (c) 60 kg: 1 quintal 45 min: 1 hour Clearly, 60 kg: 1 quintal ≠ 45 min: 1 hour Hence, the given ratios do not form a proportion. By: Harshul Siddharth

WE USE RATIO IN OUR DAILY LIFE By: Bhavesh Kaushik EXAMPLE: Suppose that Kunal weights 28 kg and Tanya weights 32 kg. SOLUTION: (Kunal’s weight): (Tanya's weight)=28 kg: 32 kg =28/32 divided by 4=7/8=7: 8 Therefore, ratio of Kunal’s weight and Tanya's weight is 7: 8 Kg

WE USE PROPORTION IN OUR DAILY LIFE By: Bhavesh Kaushik EXAMPLE: Are the two ratios 45 g: 60 g and 36 kg: 48 kg in proportion ? SOLUTION: 1 - 45 g: 60 g=45: 60=45/60=3/4=3: 4 SOLUTION: 2 -36 kg: 48 kg=36: 48=36/48=3/4=3: 4 Therefore, the ratios 45 g: 60 g and 36 kg: 48 kg are in proportion.

Ratio In a ratio x: z, x is called the antecedent and z is called the consequent. A ratio is always equivalent to itself multiplied by a nonzero no. Eg. 1 A company wants to reduce its operating cost in the ratio 2 : 3. If the operating cost was $51000 last year, what would be its target cost? Sol. Cost is to be reduced in the ratio 2: 3 Therefore, target cost : Old Cost= 2: 3 Let the target cost be x x: 51000=2: 3 x=(51000*2)/3 Therefore, x=102000/3 Therefore, the company’s target cost =34000 would be $34000. By: Eshan Uniyal

Proportion is expressing the equality of ratios such as A: B and C: D which is written as A: B=C: D or A: B: : C: D. The latter form, when spoken or written in the English language, is often expressed as: A is to B as C is to D. Again, A, B, C, D are called the terms of the proportion. A and D are called the extremes, and B and C are called the means. The equality of three or more proportions is called a continued proportion. Eg. The first three terms of a proportion are 3, 5 and 21 respectively. Find the fourth term: Sol. Let the fourth term be x. 3: 5: : 21: x =3*x=5*21 Therefore, the fouth term is 35. =3*x=105 =x=105/3 By: =35 Eshan Uniyal

Ratio In the ratio a: b, we call a as the first term or antecedent and b as the second term or consequent A ratio remains unchanged if both of it’s terms are multiplied by the same nonzero quantity. Let m ≠ 0, then clearly we have i. a∕b=ma∕mb & therefore, (a: b)=(ma: mb) ii. a∕b=(a∕m)÷(b∕m)and therefore (a: b)=(a∕m: b∕m) Eg: Divide 60$ in the ratio ¼ : 1/6 By: Sol: lcm of 4 & 6 is 12 Salman Nehru 1/4 : 1/6 = ¼ * 12 : 1/6 * 12 = 3: 2 Sum of the ratios = 3+2 = 5 First part = 360* 3/5=216$ Second part = 2/5*360=144$ Eg: The cost of an eraser is 80 paise & the cost of a pencil is 200 paise. What is the ratio of their costs in the simplest form ? Sol: cost of an eraser = 80 paise cost of a pencil = 2 rupees = 200 paise cost of an eraser : cost of the pencil = 80 : 200 =2 : 5

PROPORTION 4 Four numbers a, b, c, d are said to be in proportion, if a: b=c: d and we write, 1 If a: b: : c: d, then I. a, b, c, d are respectively known as first, second, third and fourth term. II. a and d are called extremes while b and c are called means III. If all four a, b, c, d, are in proportion then product of the means is equal to the product of the extremes. IV. We say that d is the fourth proportional to a, b, c. Examples 1)Are 22, 33, 42, 63 in proportion Sol-Product of extremes=Product of means (22*63) =(33*42) 1386=1386 Therefore, 22, 33, 42, 63 are in proportion 2) 2 A = 3 B =4 C find A: B: C By: LET 2 A = 3 B = 4 C = K Salman Nehru A= K/2, B= K/3, C= K/4 K/2 * 12= 6 K, K/3 * 12 =4 K, K/4*12=3 K 6: 4: 3

If a recipe calls for 1 egg and 2 cups of flour, the relationship of eggs to cups of flour is 1 to 2. In mathematical language, that relationship can be written in two ways: 1/2 or 1: 2 Both of these express the ratio of eggs to cups of flour: 1 to 2. If you mistakenly alter that ratio, the results may not be edible By: Ritvik Kumar

Examples of ratio and proportion Suppose the price of oranges is Rs. 20 a dozen, If we want to buy six oranges, how do we determine their cost ? As the number of oranges is half of one dozen, their cost also has to behalf. Therefore, the cost of 6 oranges is to their number half of rs. 20 i. e. Rs 10. In other words, we think that the cost of oranges in proportion Real life applications of ratio and proportion are numerous! When we prepare recipes, paint our house, or repair gears in a large machine or in a car transmission, we use ratios and proportions By: Ritvik Kumar

RATIO & PROPORTION (BY –RISHABH , CLASS –VII F) E : F I L LY I A D OUR N I ION T R O P KE PRO I & L O. I ES RAT I C F N O E ES URR C F O v US UE L A V E H PLE T M A G X N E I OW N K FOR R O. F S ) IT N 1 U 0 5. F O E 1$=RS U L A E V H E T K I L. G C N OWI E ET N G K E L L FOR , CO L O O M 2) SCH 000 1 A = F M O K 1 TH G N E R E ST H T G WIN O N K. Y R A O F W ) S 3 R LE IRL P G M 2 I : S Y IN A 1 BO S N O I ACT R F D AN T S R E UND O T ) 4

By Vardaan Sahgal U O Y K T N A H AND HAVE A NICE DAY
 Application of mathematics in practical situations
Application of mathematics in practical situations When do we use polynomials in real life
When do we use polynomials in real life Experience centered design
Experience centered design Piecewise function real life examples with answers
Piecewise function real life examples with answers Graphs in real life situations
Graphs in real life situations Practical application of calculus
Practical application of calculus Boyle's law in real life
Boyle's law in real life Practical application of solar energy
Practical application of solar energy State five practical application of batteries
State five practical application of batteries Physical significance of stokes' theorem
Physical significance of stokes' theorem Practical application
Practical application Practical application of biotechnology
Practical application of biotechnology Logical equivalence table
Logical equivalence table In march
In march Malpighian body
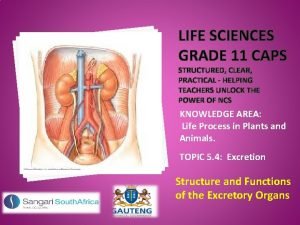
Malpighian body Life science grade 11 kidney practical
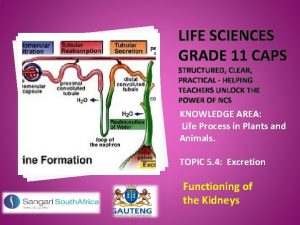
Life science grade 11 kidney practical Gaseous exchange practical grade 11
Gaseous exchange practical grade 11