Uncertainty Significant Figures and Rounding What is Uncertainty

Uncertainty, Significant Figures, and Rounding

What is Uncertainty? • All measurements fall between two divisions on a measuring device. • The distance between the two divisions is estimated. • This estimated value is the uncertainty and is expressed in a final recorded value.

Certain vs. Uncertain Digits • In the example below, we can see for certain that the leaf is greater than 3 units long. This is the certain digit. • How far between the 3 and 4 units is the tip of the leaf? • Is it 3. 6? 3. 7? 3. 5? • The digit in the tenths place is estimated – it is the uncertain digit.

Certain vs. Uncertain Digits • Let’s report the leaf’s length at 3. 7 units long. • This measurement has two significant figures – one is certain, the other is uncertain. • We cannot report the measurement as 3. 70 units – we don’t have a division in tenths! • If we reported the length as 3. 70 units we’d be telling the reader that our ruler was divided into tenths and the hundredths place was estimated.

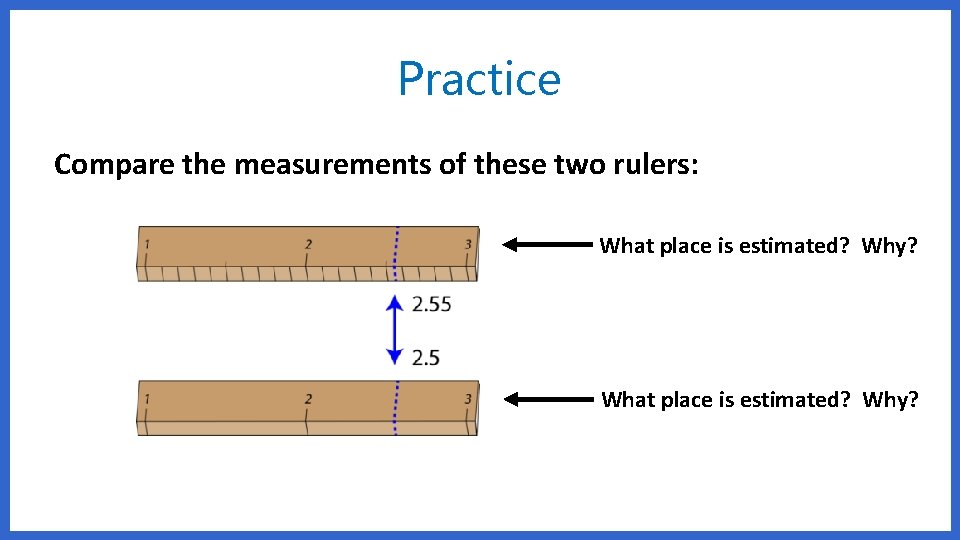
Practice Compare the measurements of these two rulers: What place is estimated? Why?

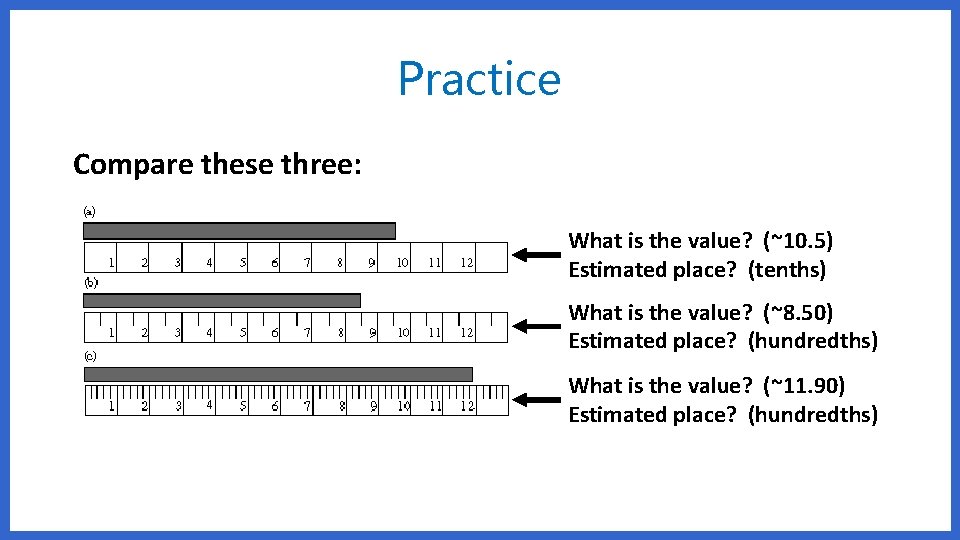
Practice Compare these three: What is the value? (~10. 5) Estimated place? (tenths) What is the value? (~8. 50) Estimated place? (hundredths) What is the value? (~11. 90) Estimated place? (hundredths)

Significant Figures • Significant Figures are digits in a measurement that reflect precision of instruments and data. • “Sig Figs” are used to keep data consistent so that experiments remain valid.

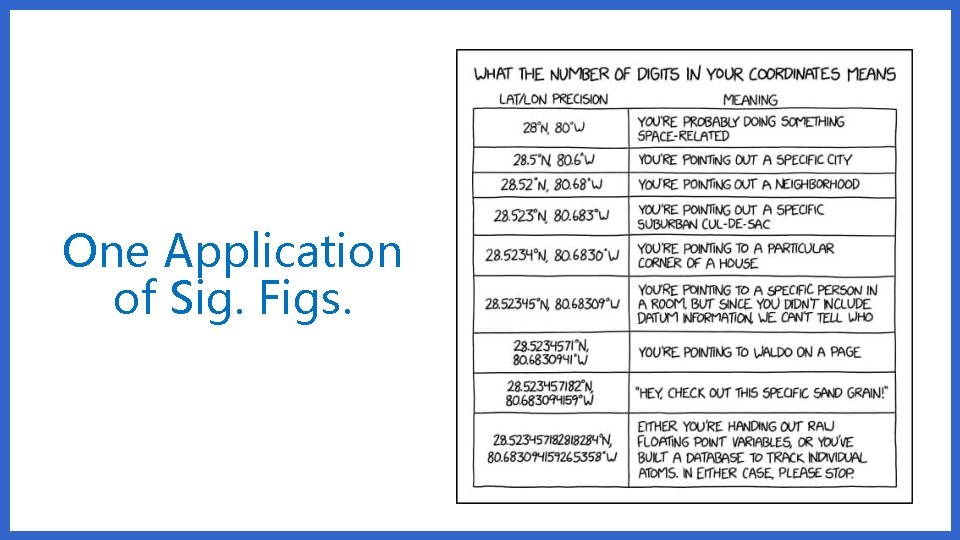
One Application of Sig. Figs.

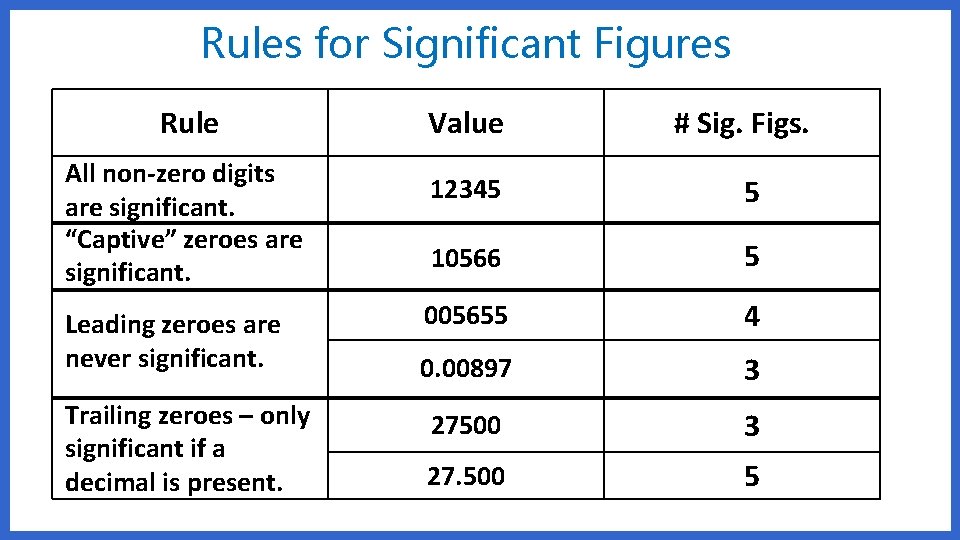
Rules for Significant Figures Rule All non-zero digits are significant. “Captive” zeroes are significant. Leading zeroes are never significant. Trailing zeroes – only significant if a decimal is present. Value # Sig. Figs. 12345 5 10566 5 005655 4 0. 00897 3 27500 3 27. 500 5

Calculations with Sig. Figs. • Multiplication and Division: • The value with the fewest sig. figs. determines the number of sig. figs. in the answer. Example: • Exception: Exact numbers. Example:

Calculations with Sig. Figs. • Addition and Subtraction: • The value with the fewest digits to the right of the decimal point determines the number of sig. figs. in the answer. Example: • Exception: Exact numbers. Example: (The 0. 5 cats is a kitten? )

Determine the number of significant figures in these: 1. 250. 7 4 2. 0. 00077 2 3. 1024 4 4. 4. 7 x 10 -5 2 5. 34000000 2 6. 1003. 4 Calculate the following and round to the correct number of significant figures. 1. (34. 5) (23. 46) 809 2. 123 / 3 40 3. (2. 61 x 10 -1) (3560. ) 929 4. 21. 78 + 45. 8 67. 6 5. 23. 888897 - 11. 2 12. 7 6. 6 - 3. 0 3

Rounding • When you perform a calculation on your calculator, you usually see many more digits than are allowed. • When do you round the value? And to what place? • In a multi-step calculation, it’s best to carry a few extra digits until the end, then round your final answer. • To what place? Think of how many significant figures you are allowed.

Rounding • What about “ 5”? • If the digit directly to the right of the final significant figure is less that 5 then the preceding digit stays the same • If it is equal to or greater than 5 then the preceding digit should be increased by one. • Round the value below to 3 significant figures. 34. 448 34. 4