Chapter 7 Counting Principles Discrete Mathematical Structures Theory

Chapter 7: Counting Principles Discrete Mathematical Structures: Theory and Applications

Learning Objectives q Learn the basic counting principles— multiplication and addition q Explore the pigeonhole principle q Learn about permutations q Learn about combinations Discrete Mathematical Structures: Theory and Applications 2

Learning Objectives q Explore generalized permutations and combinations q Learn about binomial coefficients and explore the algorithm to compute them q Discover the algorithms to generate permutations and combinations q Become familiar with discrete probability Discrete Mathematical Structures: Theory and Applications 3

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 4

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 5

Basic Counting Principles q There are three boxes containing books. The first box contains 15 mathematics books by different authors, the second box contains 12 chemistry books by different authors, and the third box contains 10 computer science books by different authors. q A student wants to take a book from one of the three boxes. In how many ways can the student do this? Discrete Mathematical Structures: Theory and Applications 6

Basic Counting Principles q Suppose tasks T 1, T 2, and T 3 are as follows: q. T 1 : Choose a mathematics book. q. T 2 : Choose a chemistry book. q. T 3 : Choose a computer science book. q Then tasks T 1, T 2, and T 3 can be done in 15, 12, and 10 ways, respectively. q All of these tasks are independent of each other. Hence, the number of ways to do one of these tasks is 15 + 12 + 10 = 37. Discrete Mathematical Structures: Theory and Applications 7

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 8

Basic Counting Principles q Morgan is a lead actor in a new movie. She needs to shoot a scene in the morning in studio A and an afternoon scene in studio C. She looks at the map and finds that there is no direct route from studio A to studio C. Studio B is located between studios A and C. Morgan’s friends Brad and Jennifer are shooting a movie in studio B. There are three roads, say A 1, A 2, and A 3, from studio A to studio B and four roads, say B 1, B 2, B 3, and B 4, from studio B to studio C. In how many ways can Morgan go from studio A to studio C and have lunch with Brad and Jennifer at Studio B? Discrete Mathematical Structures: Theory and Applications 9

Basic Counting Principles q There are 3 ways to go from studio A to studio B and 4 ways to go from studio B to studio C. q The number of ways to go from studio A to studio C via studio B is 3 * 4 = 12. Discrete Mathematical Structures: Theory and Applications 10

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 11

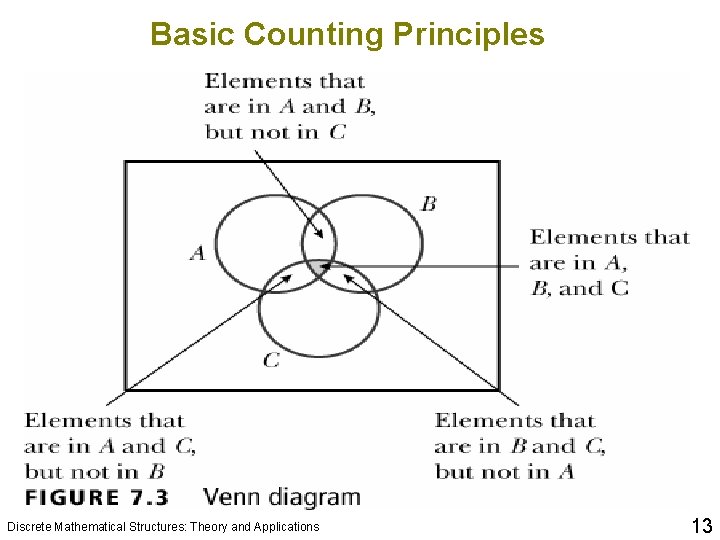
Basic Counting Principles q Consider two finite sets, X 1 and X 2. Then q This is called the inclusion-exclusion principle for two finite sets. q Consider three finite sets, A, B, and C. Then q This is called the inclusion-exclusion principle for three finite sets. Discrete Mathematical Structures: Theory and Applications 12

Basic Counting Principles Discrete Mathematical Structures: Theory and Applications 13

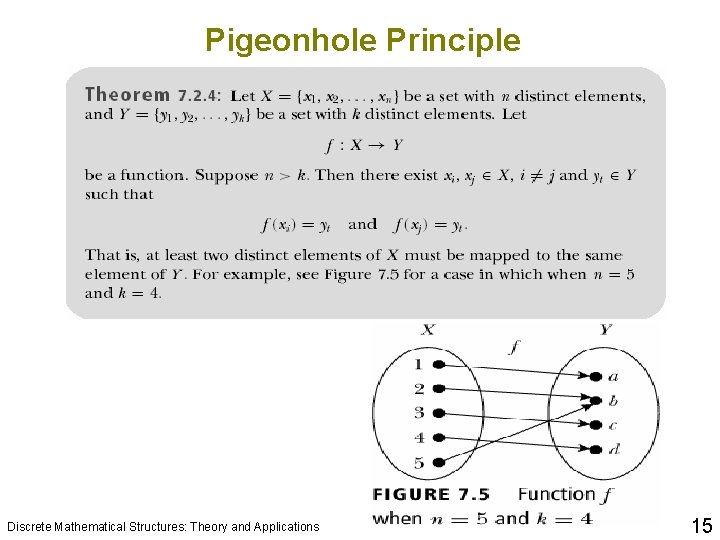
Pigeonhole Principle q. The pigeonhole principle is also known as the Dirichlet drawer principle, or the shoebox principle. Discrete Mathematical Structures: Theory and Applications 14

Pigeonhole Principle Discrete Mathematical Structures: Theory and Applications 15

Discrete Mathematical Structures: Theory and Applications 16

Pigeonhole Principle Discrete Mathematical Structures: Theory and Applications 17

Permutations Discrete Mathematical Structures: Theory and Applications 18

Permutations Discrete Mathematical Structures: Theory and Applications 19

Combinations Discrete Mathematical Structures: Theory and Applications 20

Combinations Discrete Mathematical Structures: Theory and Applications 21

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 22

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 23

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 24

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 25

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 26

Generating Permutations and Combinations Discrete Mathematical Structures: Theory and Applications 27

Discrete Mathematical Structures: Theory and Applications 28

Discrete Mathematical Structures: Theory and Applications 29

Discrete Probability q Definition 7. 8. 1 q. A probabilistic experiment, or random experiment, or simply an experiment, is the process by which an observation is made. q. In probability theory, any action or process that leads to an observation is referred to as an experiment. q. Examples include: q. Tossing a pair of fair coins. q. Throwing a balanced die. q. Counting cars that drive past a toll booth. Discrete Mathematical Structures: Theory and Applications 30

Discrete Probability q Definition 7. 8. 3 q. The sample space associated with a probabilistic experiment is the set consisting of all possible outcomes of the experiment and is denoted by S. q. The elements of the sample space are referred to as sample points. q. A discrete sample space is one that contains either a finite or a countable number of distinct sample points. Discrete Mathematical Structures: Theory and Applications 31

Discrete Probability q Definition 7. 8. 6 q. An event in a discrete sample space S is a collection of sample points, i. e. , any subset of S. In other words, an event is a set consisting of possible outcomes of the experiment. q Definition 7. 8. 7 q. A simple event is an event that cannot be decomposed. Each simple event corresponds to one and only one sample point. Any event that can be decomposed into more than one simple event is called a compound event. Discrete Mathematical Structures: Theory and Applications 32

Discrete Probability q Definition 7. 8. 8 q. Let A be an event connected with a probabilistic experiment E and let S be the sample space of E. The event B of nonoccurrence of A is called the complementary event of A. This means that the subset B is the complement A’ of A in S. q In an experiment, two or more events are said to be equally likely if, after taking into consideration all relevant evidences, none can be expected in reference to another. Discrete Mathematical Structures: Theory and Applications 33

Discrete Probability Discrete Mathematical Structures: Theory and Applications 34

Discrete Probability q Axiomatic Approach q Analyzing the concept of equally likely probability, we see that three conditions must hold. 1. The probability of occurrence of any event must be greater than or equal to 0. 2. The probability of the whole sample space must be 1. 3. If two events are mutually exclusive, the probability of their union is the sum of their respective probabilities. q These three fundamental concepts form the basis of the definition of probability. Discrete Mathematical Structures: Theory and Applications 35

Discrete Probability Discrete Mathematical Structures: Theory and Applications 36

Discrete Probability Discrete Mathematical Structures: Theory and Applications 37

Discrete Probability Discrete Mathematical Structures: Theory and Applications 38

Discrete Probability q Conditional Probability q. Consider the throw of two distinct balanced dice. To find the probability of getting a sum of 7, when it is given that the digit in the first die is greater than that in the second. q. In the probabilistic experiment of throwing two dice the sample space S consists of 6 * 6 = 36 outcomes. q. Assume that each of these outcomes is equally likely. Let A be the event: The sum of the digits of the two dice is 7, and let B be the event: The digit in the first die is greater than the second. Discrete Mathematical Structures: Theory and Applications 39

Discrete Probability q Conditional Probability q. A : {(6, 1), (5 , 2), (4, 3), (3, 4), (2, 5), (1, 6)} q. P(A)=6/36 q. B : {(6, 1), (6, 2), (6, 3), (6, 4), (6, 5), (5 , 1), (5 , 2), (5 , 3), (5 , 4), (4, 1), (4, 2), (4, 3), (3, 1), (3, 2), (2, 1)}. q. P(B)= 15/36=0. 417 Discrete Mathematical Structures: Theory and Applications 40

Discrete Probability q Conditional Probability q. Let C be the event: The sum of the digits in the two dice is 7 but the digit in the first die is greater than the second. Then C : {(6, 1), (5 , 2), (4, 3)} = A ∩ B. q. P(A ∩ B)=3/36=0. 083 q. P(A|B)=0. 083/0. 417=0. 199 Discrete Mathematical Structures: Theory and Applications 41