Chapter 4 Congruent Triangles Section 4 1 Congruent

Chapter 4 Congruent Triangles

Section 4. 1 Congruent Figures

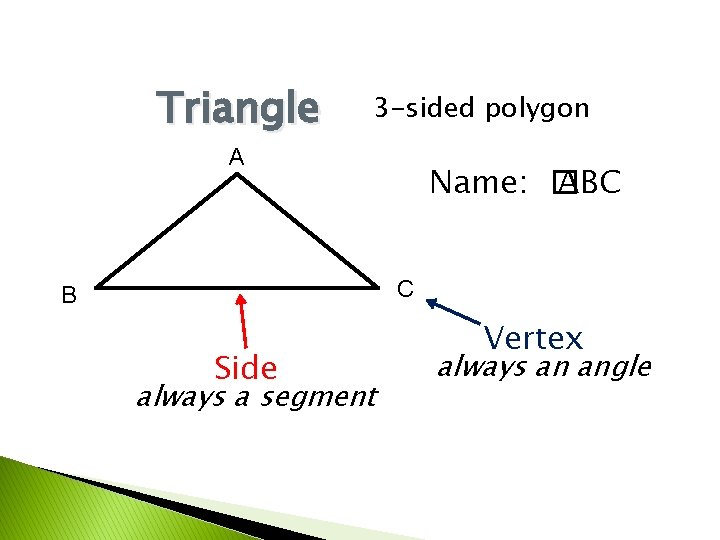
Triangle 3 -sided polygon A Name: � ABC C B Side always a segment Vertex always an angle

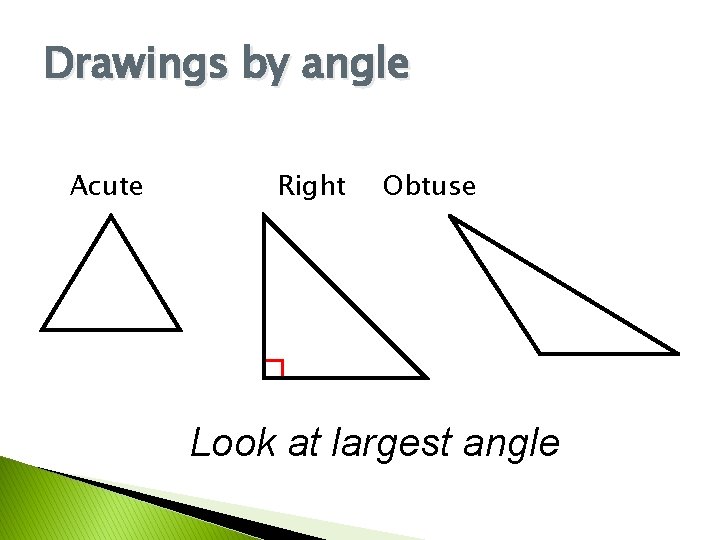
Classify by Angle Measures � Acute - all angles less than 90° � Right - one angle that is exactly 90° � Obtuse - one angle that is more than 90°

Drawings by angle Acute Right Obtuse Look at largest angle

More definitions � Opposite - travel across the triangle opposite of a side is an angle opposite of an angle is a side � Adjacent - touching / right next to

Congruence If two shapes are exactly the same size and shape, they are said to be congruent

Corresponding “parts” � When two shapes are congruent, there is a correspondence between angles and sides (parts) � Sides in similar spots match up � Angles in similar spots match up

Congruent Triangles If 2 triangles are , there are 7 congruency statements that can be written • 1 about triangles • 3 about sets of sides

� BOY � MAN Angles B M O A Y N match up one letter at a time (1 st letters) (middle letters) (last letters)

� BOY � MAN Sides - match up two letters at a time BO MA (1 st/middle letters) OY AN (middle/last letters) BY MN (1 st/last letters)

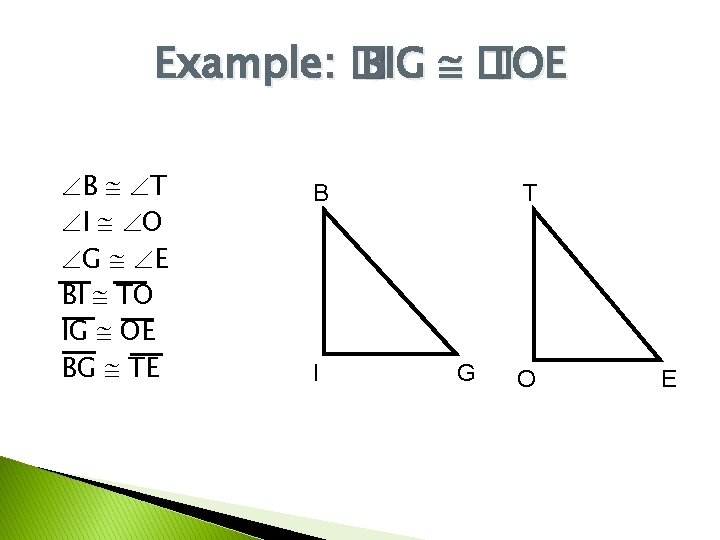
Example: � BIG � TOE B T I O G E BI TO IG OE BG TE B I T G O E

Third Angle Theorem � If two angles of one triangle are congruent to two angles of a second triangle, then the third angles must also be congruent x 50 x 60 50 60

Are triangles congruent? � In this section, ◦ Need 6 sets of congruent parts ◦ Can use vertical angles �Angles on opposite sides of an ‘X’ ◦ Use definitions of words given ◦ Use reflexive - something is equal to itself

Homework � Page 222 � 8 -30 even, 36 -40 all

Section 4 -2 Triangle Congruence by SSS and SAS

Question No need to put this in your notes Do we really need 6 sets of congruent parts to PROVE that triangles are congruent? NO (Thank goodness!)

Definition of Included � Included means contained within ◦ An included angle is between two sides Ex. B is included between AB and BC ◦ An included side is between two B angles Ex. BC is included between B and C A C

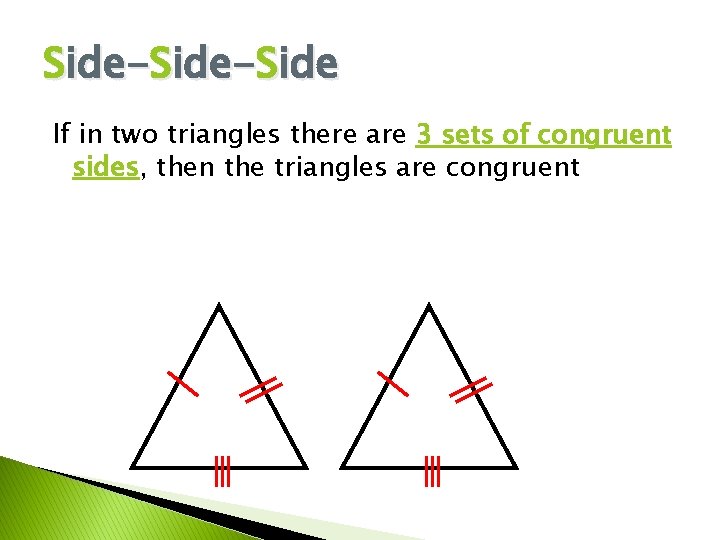
Side-Side If in two triangles there are 3 sets of congruent sides, then the triangles are congruent

Side-Angle-Side If in two triangles, there are two sets of congruent sides and their included angles are also congruent, then the triangles are congruent

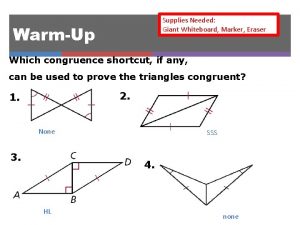
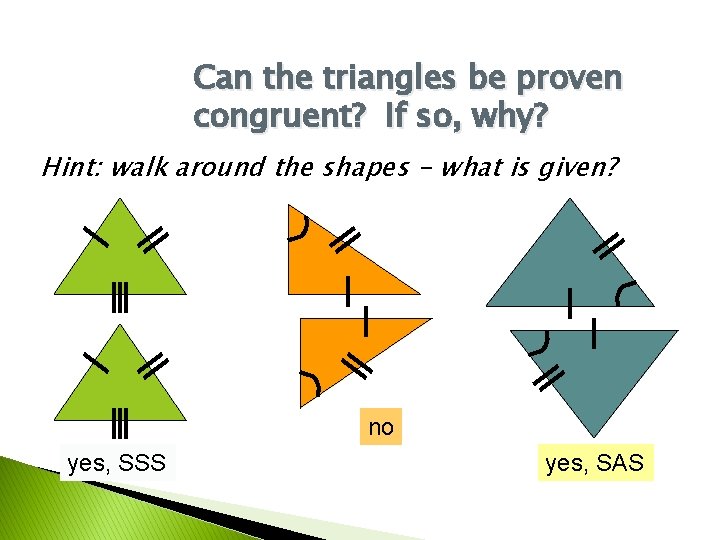
Can the triangles be proven congruent? If so, why? Hint: walk around the shapes - what is given? no yes, SSS yes, SAS

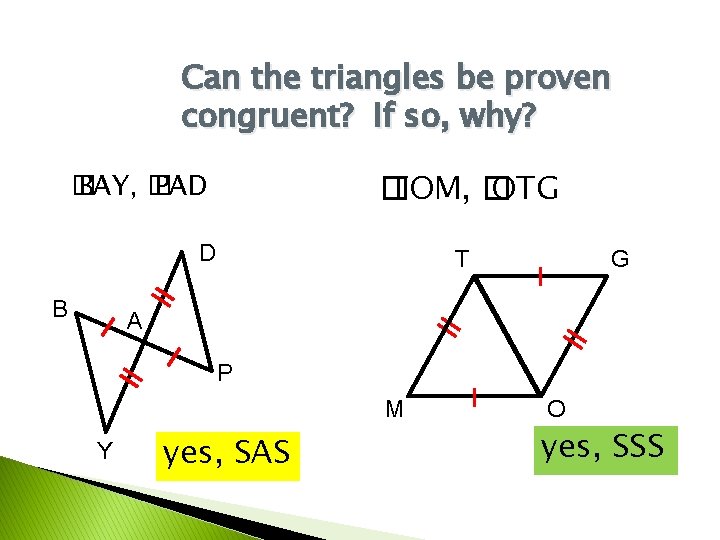
Can the triangles be proven congruent? If so, why? � TOM, � OTG � BAY, � PAD D B T G A P M Y yes, SAS O yes, SSS

Triangle Congruence Proofs � NEED 3 sets of congruent parts � MUST SHOW 3 sets of congruent parts in proof � THEN can say triangles are congruent

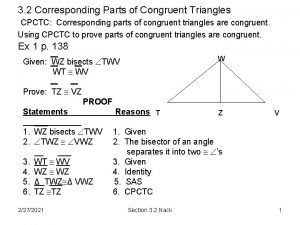
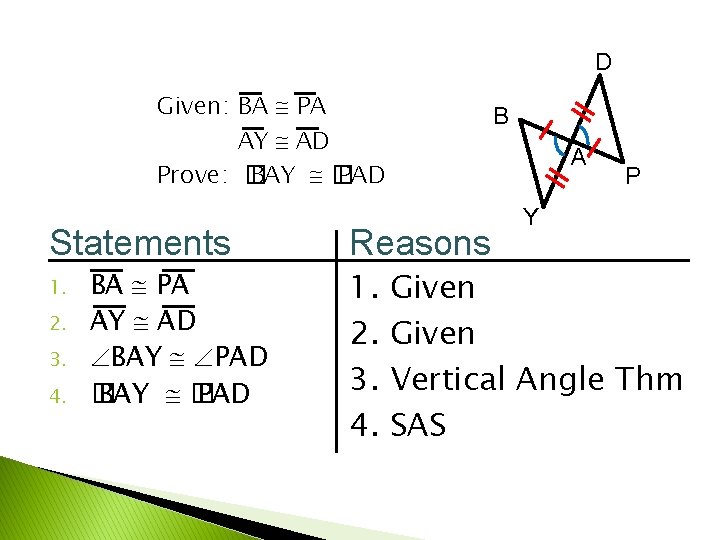
D Given: BA PA AY AD Prove: � BAY � PAD Statements 1. 2. 3. 4. BA PA AY AD BAY PAD � BAY � PAD Reasons B A P Y 1. Given 2. Given 3. Vertical Angle Thm 4. SAS

Homework � Page 230 � 1 -6, 11 -14, 24 -26

Section 4. 3 Triangle Congruence by ASA and AAS

Angle-Side-Angle If in 2 triangles there are 2 sets of angles and their included sides are also , then the triangles are

Angle-Side If in 2 triangles, there are 2 sets of angles and a set of NON-included sides are also , then the triangles are

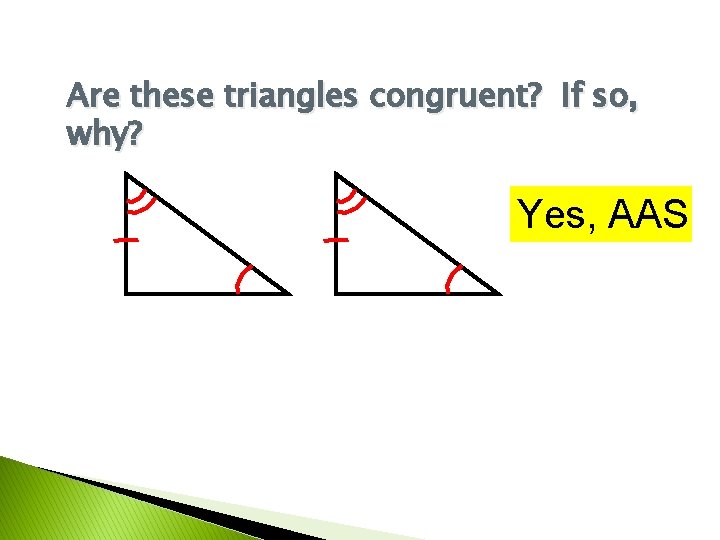
Are these triangles congruent? If so, why? Yes, AAS

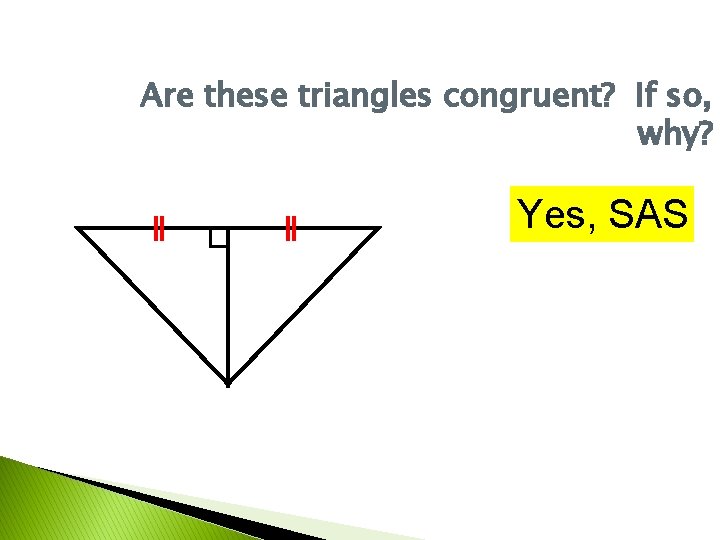
Are these triangles congruent? If so, why? Yes, SAS

Are these triangles congruent? If so, why? No

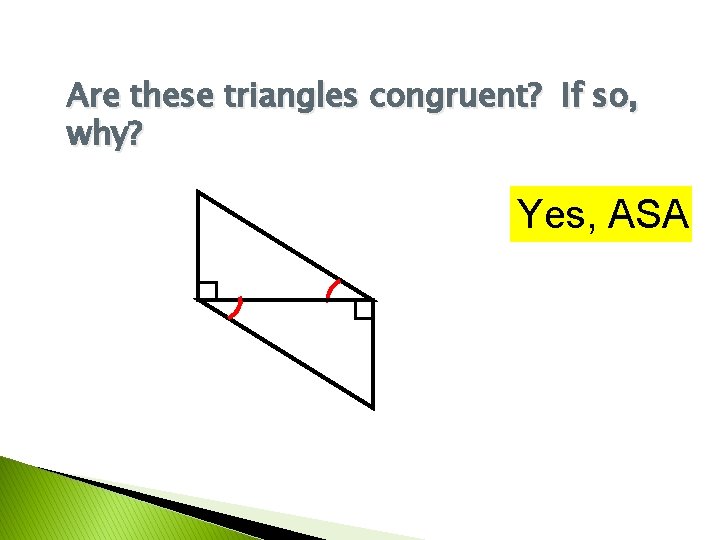
Are these triangles congruent? If so, why? Yes, ASA

What is needed to use. . AAS? O G ASA? N U SAS? CO MG C N O G U M

A Given: AB || CD, A D Prove: � ABC � DCB Statements 1. 2. 3. 4. 5. AB || CD ABC DCB A D CB � ABC � DCB C B D Reasons 1. Given 2. Alt Interior Thm 3. Given 4. Reflexive Property 5. AAS

Homework � Page 238 � 8, 9, 13, 16 -18

Section 4 -4 Using Congruent Triangles

Corresponding Parts of Congruent Figures � Those “parts” are congruent � Cannot use until a statement about congruent triangles has been made � Used when showing another set of parts are congruent

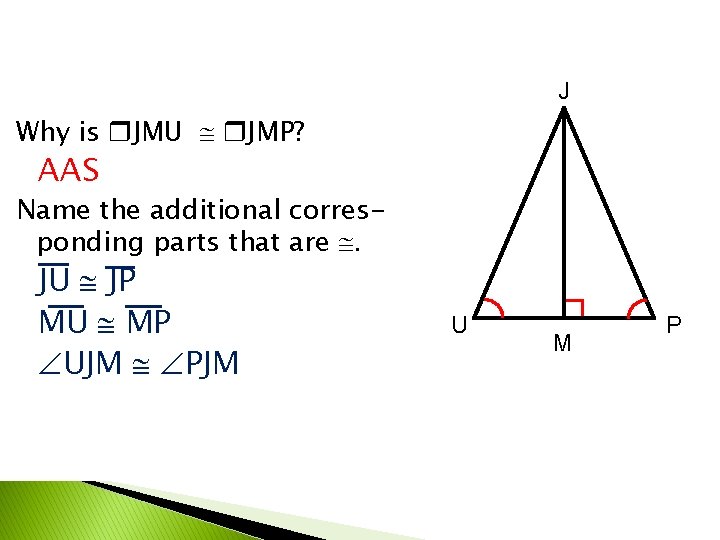
J Why is JMU JMP? AAS Name the additional corresponding parts that are . JU JP MU MP UJM PJM U M P

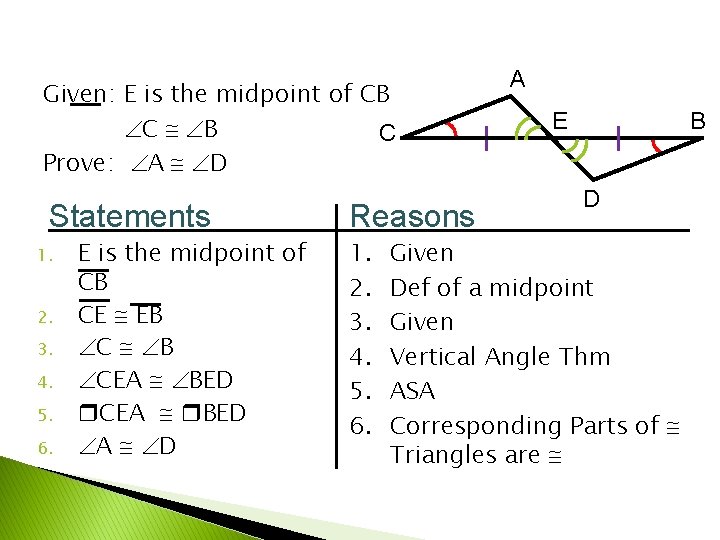
Given: E is the midpoint of CB C Prove: A D Statements 1. 2. 3. 4. 5. 6. E is the midpoint of CB CE EB C B CEA BED A D Reasons 1. 2. 3. 4. 5. 6. A E B D Given Def of a midpoint Given Vertical Angle Thm ASA Corresponding Parts of Triangles are

Section 4. 5 Isosceles and Equilateral Triangles

Classify by side length � Scalene - all sides different length � Isosceles - at least 2 sides of equal length � Equilateral - all 3 sides have equal length ◦ also called equiangular because all angles are equal

Drawings by sides Scalene Isosceles Equilateral Look for tick marks

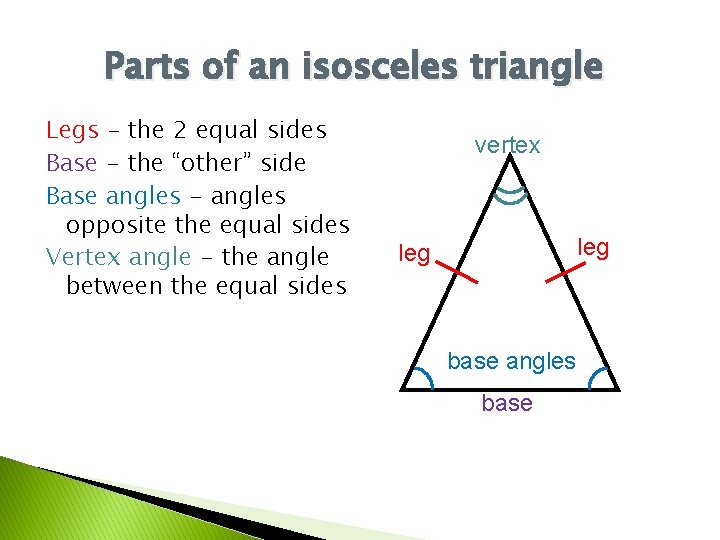
Parts of an isosceles triangle Legs - the 2 equal sides Base - the “other” side Base angles - angles opposite the equal sides Vertex angle - the angle between the equal sides vertex leg base angles base

� Base Angles Theorem ◦ If two sides of a triangle are congruent, then the angles opposite them are also congruent. � Converse of the Base Angles Theorem ◦ If two angles of a triangle are congruent, then the sides opposite them are also congruent.

A triangle is equilateral if and only if it is equiangular. This means that every equilateral triangle is equiangular.

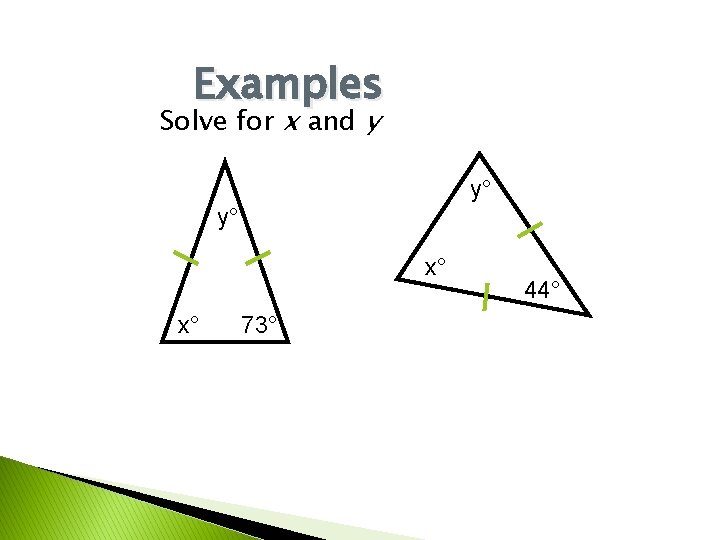
Examples Solve for x and y y° y° x° x° 73° 44°

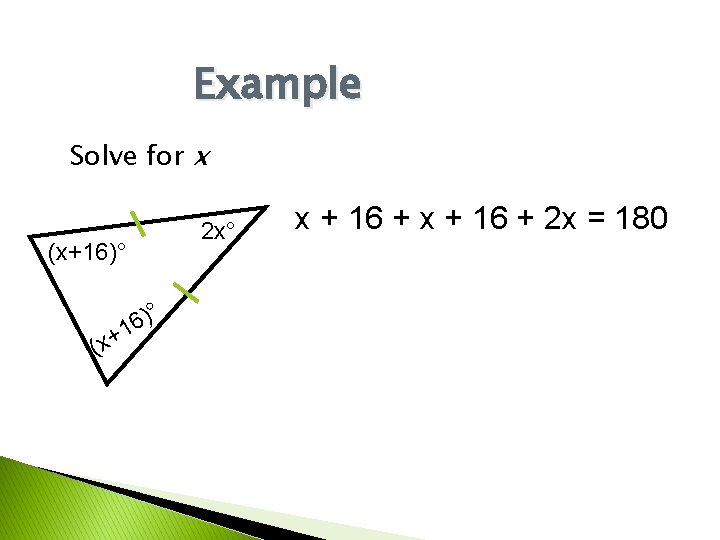
Example Solve for x (x+16)° (x+ )° 6 1 2 x° x + 16 + 2 x = 180

Special Vocabulary For a right triangle ◦ Legs - the 2 sides that form the right angle ◦ Hypotenuse - the side opposite the right angle

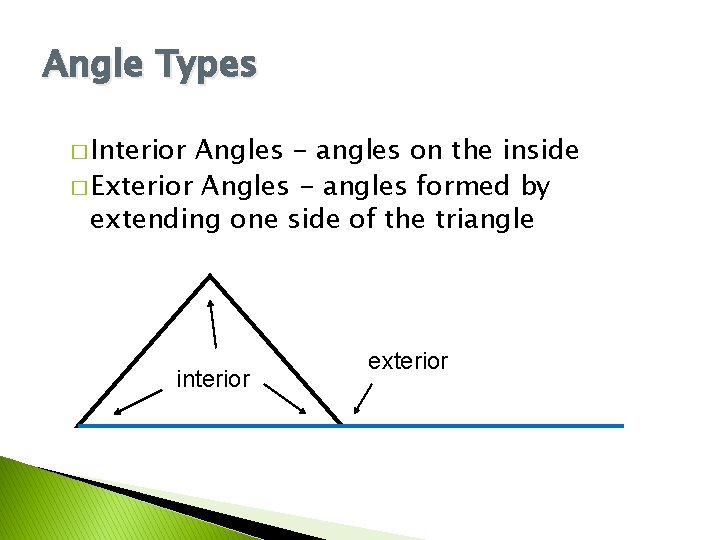
Angle Types � Interior Angles - angles on the inside � Exterior Angles - angles formed by extending one side of the triangle interior exterior

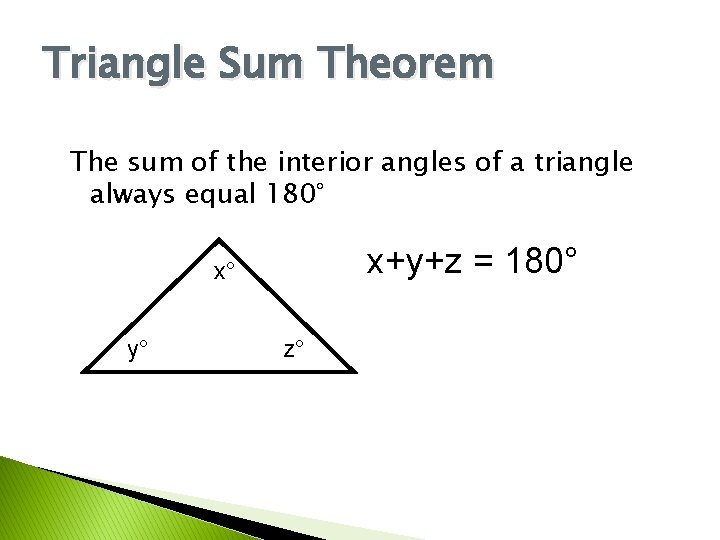
Triangle Sum Theorem The sum of the interior angles of a triangle always equal 180° x+y+z = 180° x° y° z°

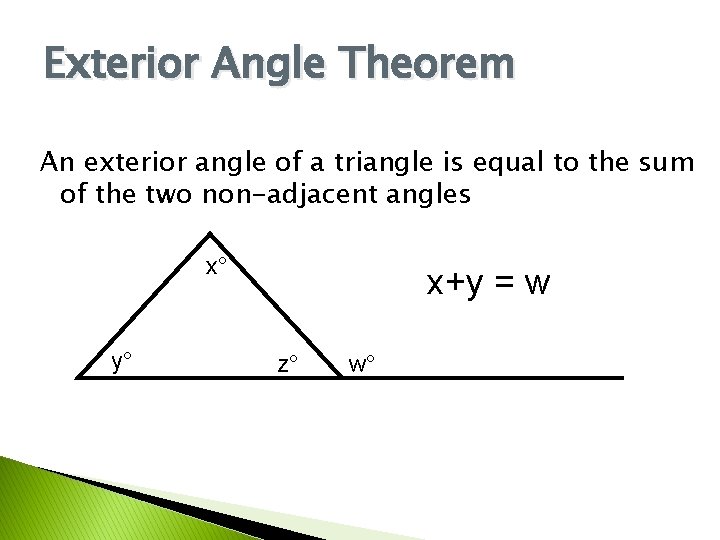
Exterior Angle Theorem An exterior angle of a triangle is equal to the sum of the two non-adjacent angles x° y° x+y = w z° w°

Right Triangle In a right triangle, the two acute angles are ALWAYS complementary x + y = 90° x y

Example Find the value of x x° (x + 10)° x + 10 + 78 = 180 78°

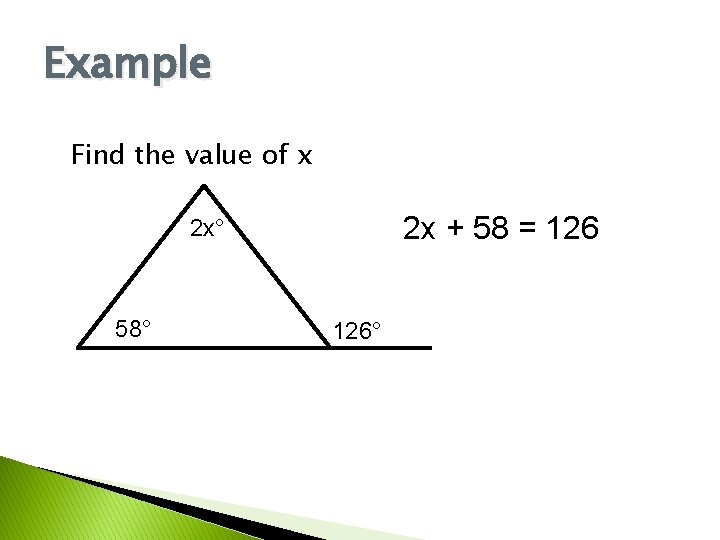
Example Find the value of x 2 x + 58 = 126 2 x° 58° 126°

Section 4 -6 Congruence in Right Triangles

Hypotenuse-Leg If in two right triangles, the hypotenuse and a set of legs are congruent, then the triangles are congruent