Chapter 4 ACCELERATION What is Acceleration Acceleration change

Chapter 4 ACCELERATION

What is Acceleration? Acceleration: change in velocity over the time interval over which it occurred

Average Acceleration Average acceleration is the ratio of change in velocity over change in time. v – v Δv 2 1 a= = t 2 – t 1 Δt

Average Acceleration Example: The velocity of a car increases from 2. 0 m/s at 1. 0 s to 16 m/s at 4. 5 s. What is the car’s average acceleration? 16 m/s – 2. 0 m/s 14 m/s 2 4. 5 s – 1. 0 s 3. 5 s = = 4 m/s a=

Average Acceleration Example: A car goes faster and faster backwards down a long driveway. We define forward velocity as positive, so backward velocity is negative. The car’s velocity changes from -2. 0 m/s to -9. 0 m/s in a 2. 0 -s time interval. Find the acceleration.

Average Acceleration Solution: velocity change, Δv = -9. 0 m/s – (-2. 0 m/s) = -7. 0 m/s average acceleration = Δv / Δt = -7. 0 m/s / 2 s = -3. 5 m / s^2

Average acceleration vs. Instantaneous acceleration Average acceleration is calculated over a time interval. Instantaneous acceleration occurs at a specific time.

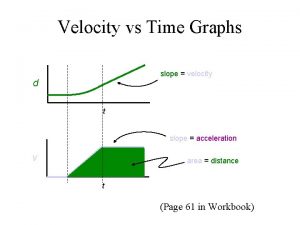
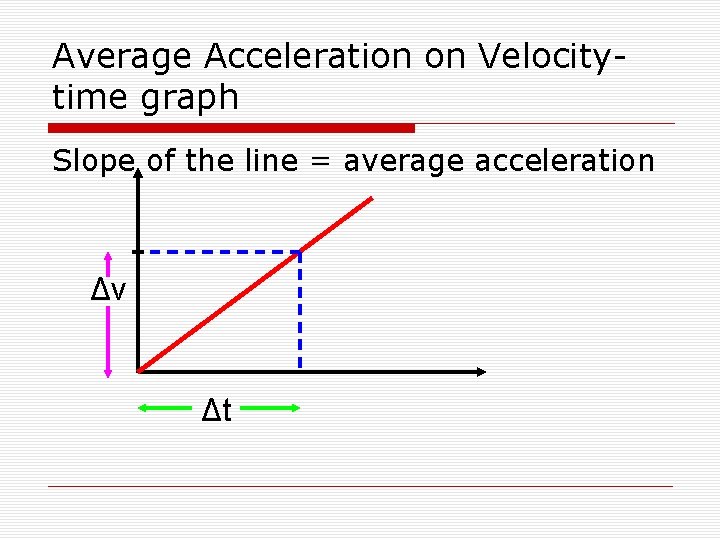
Average Acceleration on Velocitytime graph Slope of the line = average acceleration Δv Δt

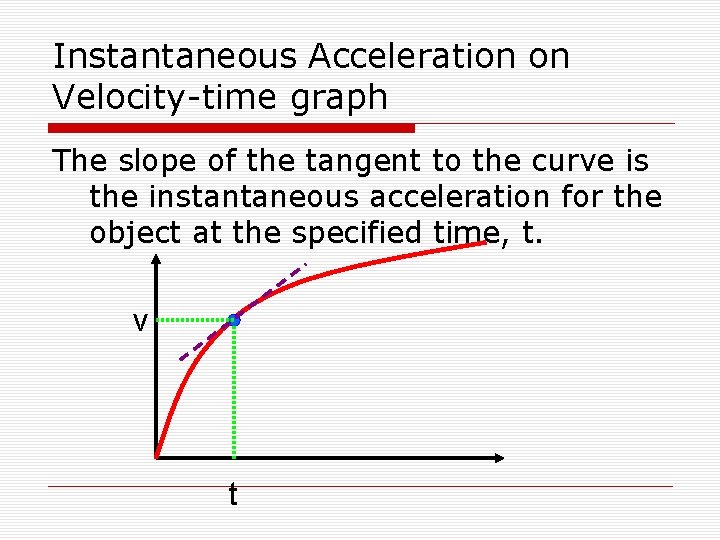
Instantaneous Acceleration on Velocity-time graph The slope of the tangent to the curve is the instantaneous acceleration for the object at the specified time, t. v t

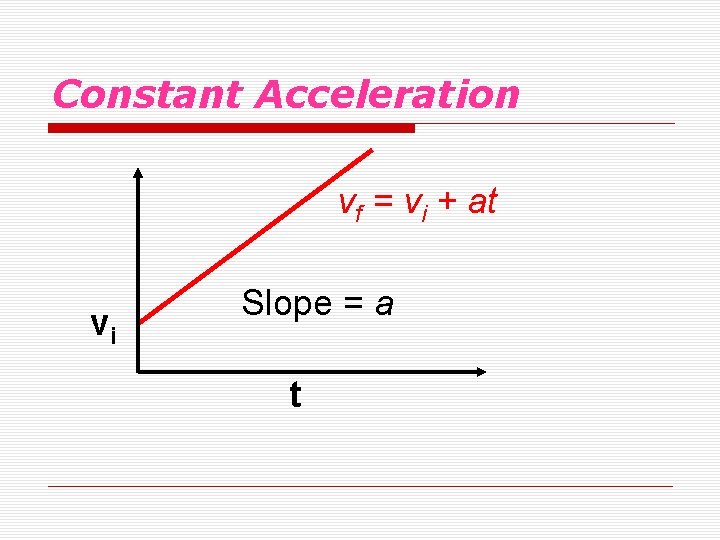
Constant Acceleration that does not change in time is uniform or constant acceleration. It is represented by a straight line on a velocity-time graph.

Constant Acceleration vf = vi + at vi Slope = a t

Constant Acceleration Example: If a car with a velocity of 2. 0 m/s at t = 0 accelerates at a rate of +4. 0 m/s^2 for 2. 5 s, what is its velocity at time t = 2. 5 s? Using the equation of constant acceleration: vf = vi + at = +2. 0 m/s + (+4. 0 m/s 2)(2. 5 s) = 12 m/s

Displacement when velocity and time are known Average velocity: v = ½ (vf + vi) Average velocity: v = d/t Combining the two equations d/t = ½ (vf + vi) d = ½ (vf + vi) t

Displacement when acceleration and time are known Starting with the displacement equation: d = ½ (vf + vi) t and using the final velocity equation: vf = vi + at Combining the two equations: d = ½ (vi + at + vi) t = ½ (2 vi + at) t d = vit + ½ at 2

Displacement when velocity and acceleration are known Starting with d = ½ (vf + vi) t and vf = vi + at Substituting t = (vf – vi)/a into d = ½ (vf + vi) t d = ½ (vf + vi) (vf – vi) /a = (vf 2 – vi 2) / 2 a Solve for vf 2: vf 2 = vi 2 + 2 ad

Equations of Motion for Uniform Acceleration Equations Variables vf = vi + at vi vf a t d = ½ (vf + vi) t vi vf d t d = vit + ½ at 2 vi a d t vf vi vf a d 2 = vi 2 + 2 ad

Example: What is the displacement of a train as it is accelerated uniformly from +11 m/s to +33 m/s in a 20. 0 -s interval?

Example: A car starting from rest accelerates uniformly at +6. 1 m/s 2 for 7. 0 s. How far does the car move?

Example: An airplane must reach a velocity of 71 m/s for takeoff. If the runway is 1. 0 km long, what must the constant acceleration be?

Example: The time the Demon Drop ride at Cedar Point, Ohio is freely falling for 1. 5 s. a. What is the velocity at the end of this time? b. How far does it fall?

Problems 1. Find the uniform acceleration that causes a car’s velocity to change from 32 m/s to 96 m/s in an 8. 0 -s period. 96 m/s – 32 m/s = 8. 0 m/s^2 8. 0 s

Problems 2. Rocket-powered sleds are used to test the responses of humans to acceleration. Starting from rest, one sled can reach a speed of 444 m/s in 1. 80 s and can be brought to a stop again in 2. 15 s.

Problems a. Calculate the acceleration of the sled when starting and compare it to the acceleration due to gravity, 9. 80 m/s 2. a = 444 m/s – 0 = 247 m/s 2 1. 80 s 247 / 9. 8 = 25. 2

Problems b. Find the acceleration of the sled when braking and compare it to the magnitude of the acceleration due to gravity. a = 0 – 444 m/s = - 207 m/s 2 2. 15 s 207 m/s 2 = 21. 1 9. 8 m/s 2

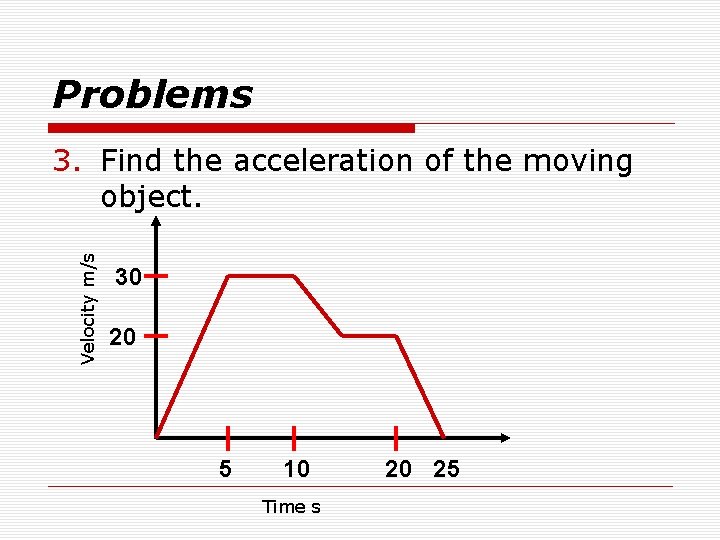
Problems Velocity m/s 3. Find the acceleration of the moving object. 30 20 5 10 Time s 20 25

Problems a. During the first five seconds of travel. a = 30 m/s – 0 m/s = 6 m/s 2 5 s b. Between the fifth and the tenth second of travel. a. 30 m/s – 30 m/s = 0 5 s

Problems c. Between the tenth and the fifteenth second of travel. a = 20 m/s – 30 m/s = -2 m/s 2 5 s d. Between the twentieth and the twentyfifth second of travel. a = 0 – 20 m/s = -4 m/s 2 5 s

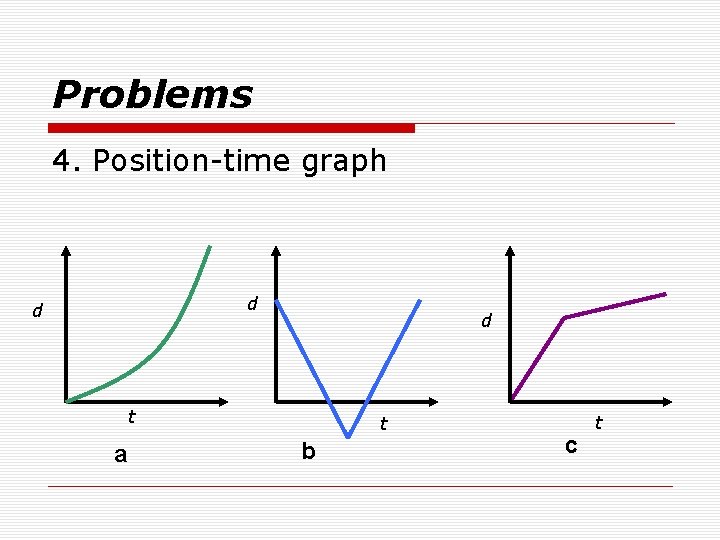
Problems 4. Position-time graph d d d t a t b c t

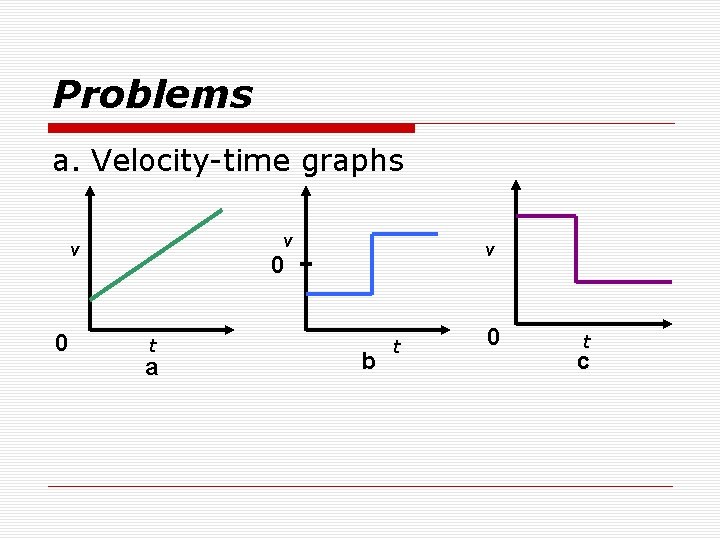
Problems a. Velocity-time graphs v v 0 t a b t 0 t c

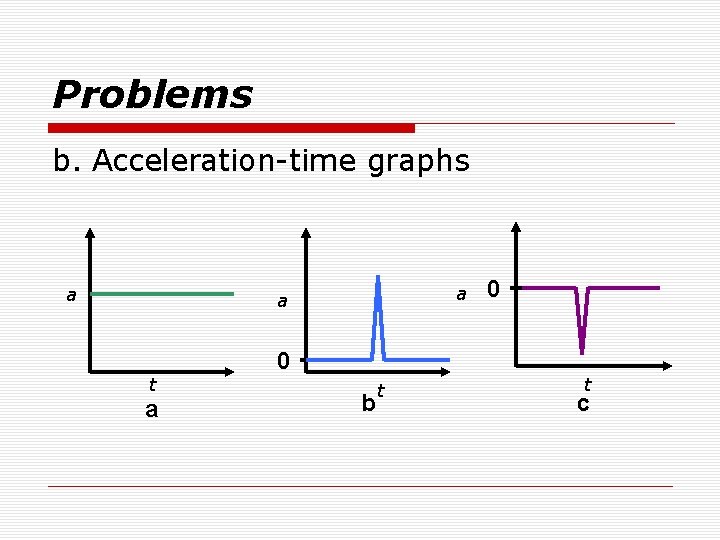
Problems b. Acceleration-time graphs a a a t a 0 b t 0 t c

Problems 5. A car with a velocity of 22 m/s is accelerated uniformly at the rate of 1. 6 m/s^2 for 6. 8 s. What is its final velocity? vf = vi + at = 22 m/s + (1. 6 m/s 2)(6. 8 s) = 33 m/s

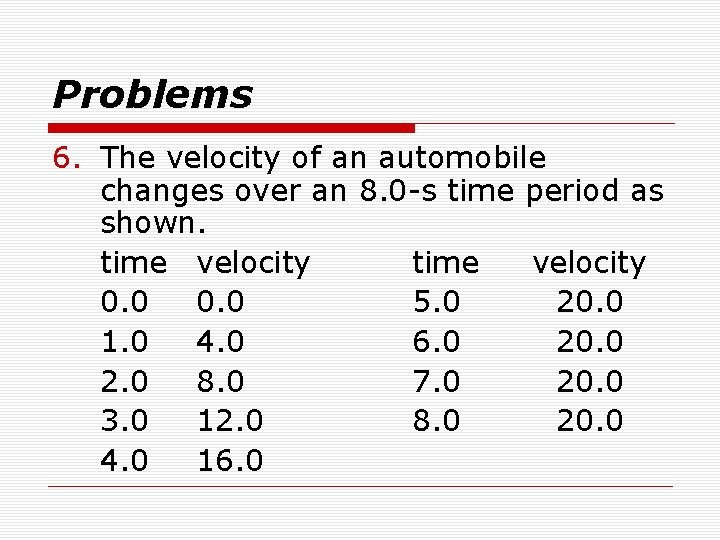
Problems 6. The velocity of an automobile changes over an 8. 0 -s time period as shown. time velocity 0. 0 5. 0 20. 0 1. 0 4. 0 6. 0 20. 0 2. 0 8. 0 7. 0 20. 0 3. 0 12. 0 8. 0 20. 0 4. 0 16. 0

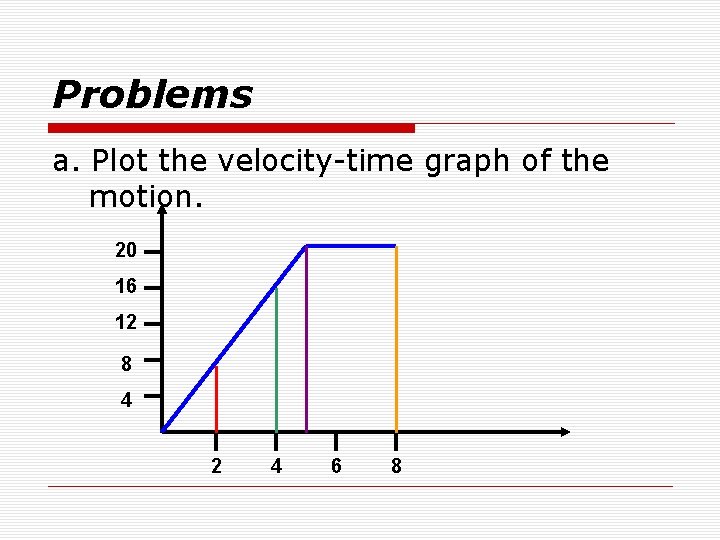
Problems a. Plot the velocity-time graph of the motion. 20 16 12 8 4 2 4 6 8

Problems b. Determine the displacement of the car the first 2. 0 s. (displacement is the area under the curve) d = ½ bh = ½ (2. 0 s)(8. 0 m/s – 0) =8 m

Problems c. What displacement does the car have during the first 4. 0 s? d = ½ bh = ½ (4. 0 s)(16. 0 m/s – 0) = 32 m

Problems d. What displacement does the car have during the entire 8. 0 s? d = ½ bh + bh = ½ (5. 0 s)(20. 0 m/s – 0) + (8. 0 s – 5. 0 s)(20. 0 m/s) = 110 m

Problems e. Find the slope of the line between t = 0 s and t = 4. 0 s. What does this slope represent? a = Δv/ Δt = (16 m/s – 0 m/s)/(4. 0 s – 0 s) = 4 m/s 2

Problems f. Find the slope of the line between t = 5. 0 s and t = 7. 0 s. What does this slope indicates. a = Δv/ Δt = (20 m/s – 20 m/s)/(7. 0 s – 5. 0 s) = 0 constant velocity

Problems 7. Figure 4 -20 shows the position-time and velocity-time graphs of a karate expert using a fist to break wooden boards.

Problems 7 a. Use the velocity-time graph to describe the motion of the expert’s fist during the first 10 ms. The fist moves downward at about 13 m/s for about 5 ms. It then suddenly comes to a halt (accelerates).

Problems 7 b. Estimate the slope of the velocity-time graph to determine the acceleration of the fist when it suddenly stops. a = Δv/ Δt = (0 – (-13 m/s))/(7. 5 ms – 5. 0 ms)) = 5200 m/s 2

Problems 7 c. Express the acceleration as a multiple of the gravitational acceleration, g = 9. 8 m/s^2. (5200 m/s^2)/(9. 8 m/s^2) = 530

Problems 7 d. Determine the area under the velocitytime curve to find the displacement of the fist in the first 6 ms. Compare with the position-time graph. The area is almost rectangular: (-13 m/s)(0. 006 s) = -8 cm. This is in agreement with the position-time graph where the hand moves from +8 cm to 0 cm, for a net displacement of – 8 cm.

Problems 8. A supersonic jet flying at 145 m/s is accelerated uniformly at the rate of 23. 1 m/s^2 for 20 s.

Problems 8 a. What is its final velocity? s) vf = vi + at = 145 m/s + (23. 1 m/s^2)(20. 0 = 607 m/s

Problems b. The speed of sound in air is 331 m/s. How many times the speed of sound is the plane’s final speed? x = (607 m/s) / (331 m/s) = 1. 83 times the speed of sound

Problems 9. Determine the final velocity of a proton that has an initial velocity of 2. 35 x 10^5 m/s and then is accelerated uniformly in an electric field at the rate of -1. 10 x 10^12 m/s^2 for 1. 50 x 10^-7 s. vf = vi + at = 235 m/s + (-1. 10 x 10^12 m/s^2 )(1. 50 x 10^-7 s) = 7. 0 x 10^4 m/s

Problems 10. Determine the displacement of a plane that is uniformly accelerated from 66 m/s to 88 m/s in 12 s. d = (vf + vi)t / 2 = (88 m/s + 66 m/s)(12 s) / 2 = 924 m

Problems 11. How far does a plane fly in 15 s while its velocity is changing from +145 m/s to +75 m/s at a uniform rate of acceleration? d = (vf + vi)t / 2 = (75 m/s + 145 m/s)(15 s) / 2 = 1650 m

Problems 12. A car moves at 12 m/s and coasts up a hill with a uniform acceleration of -1. 6 m/s^2.

Problems a. How far has the car traveled after 6. 0 s? d = vit + ½ at^2 = (12 m/s)(6 s) + ½ (-1. 6 m/s)(6. 0)^2 = 43 m b. How far has it gone after 9. 0 s? d = vit + ½ at^2 = (12 m/s)(9 s) + ½ (-1. 6 m/s)(9. 0)^2

Problems 13. Four cars start from rest. Car A accelerates at 6. 0 m/s^2, car b at 5. 4 m/s^2, car C at 8. 0 m/s^2, and car D at 12 m/s^2.

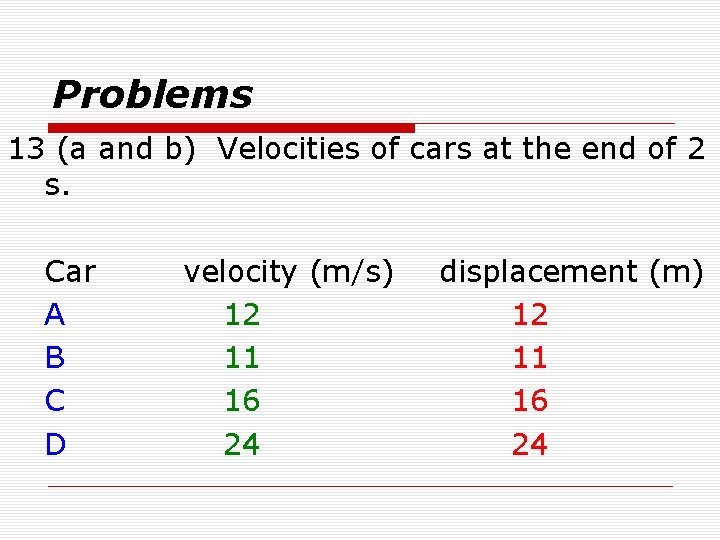
Problems 13 (a and b) Velocities of cars at the end of 2 s. Car A B C D velocity (m/s) 12 11 16 24 displacement (m) 12 11 16 24

Problems 13 c. What conclusions do you reach about the velocity attained and the displacement of a body starting from rest at the end of the first 2. 0 s of acceleration? The displacement traveled and velocity attained are numerically the same at the end of two seconds.

Problems 14. An astronaut drops a feather from 1. 2 m above the surface of the moon. If the acceleration of gravity on the moon is 1. 62 m/s^2, how long does it take the feather to hit the surface?

Problems 14. d = vit + ½ at^2 t = √(2 d/g) = √((2)(-1. 2 m)/(-1. 6 m/s 2)) = 1. 2 s

Problems 15. Table 4 -4 is a table of displacement and velocities of a ball at the end of each second for the first 5. 0 s of free fall from rest. time displacement velocity 0. 0 1. 0 -4. 9 -9. 8 2. 0 -19. 6 3. 0 -44. 1 -29. 4 4. 0 -78. 4 -39. 2 5. 0 -122. 5 -49. 0

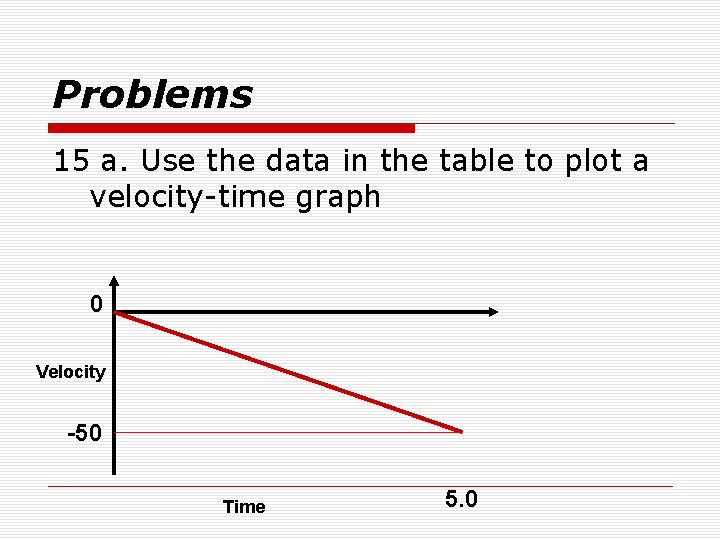
Problems 15 a. Use the data in the table to plot a velocity-time graph 0 Velocity -50 Time 5. 0

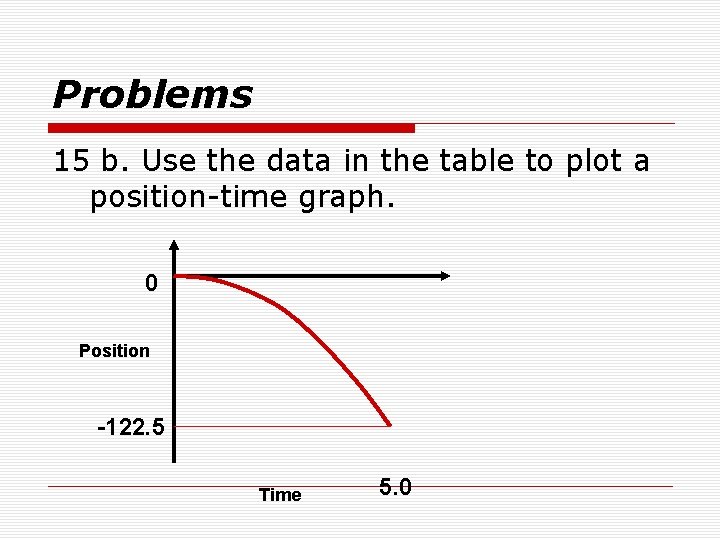
Problems 15 b. Use the data in the table to plot a position-time graph. 0 Position -122. 5 Time 5. 0

Problems 15 c. Find the slope of the curve at the end of 2. 0 and 4. 0 s on the position-time graph. What are the approximate slopes? Do these values agree with the table of velocity? at 2. 0 s: slope = (-40 – (-1))/(3. 0 – 1. 0) = -20 m/s at 4. 0 s: slope = (-118 – (-40))/(5. 0 – 3. 0) = -39 m/s Yes, the values agree.

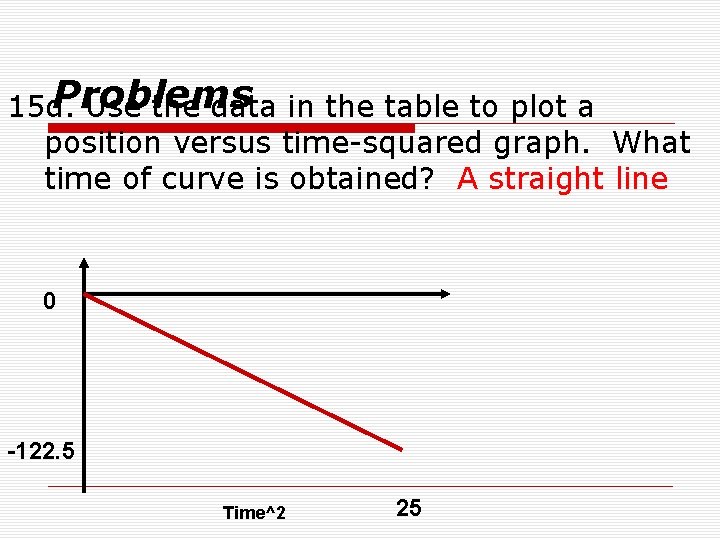
Problems 15 d. Use the data in the table to plot a position versus time-squared graph. What time of curve is obtained? A straight line 0 -122. 5 Time^2 25

Problems 15 e. Find the slope of the line at any point. Explain the significance of the value you obtain. slope = (-122. 5 – 0)/(25 – 0) = -4. 9 m/s^2 The slope is ½ g

Problems 15 f. Does this curve agree with the equation d = ½ gt^2? yes, since it is a straight line y = mx + b where y is d, m is ½ g, x is t^2 and b is 0.

Problems 16. A plane travels 5. 0 x 10^2 m while being accelerated uniformly from rest at the rate of 5. 0 m/s^2. What final velocity does it attain? vf ^2 = vi^2 + 2 ad vf = √(vi^2 + 2 ad) = √(0^2+ 2(5. 0)(500)) = 71 m/s

Problems 17. A race car can be slowed with a constant acceleration of -11 m/s 2. a. If the car is going 55 m/s , how many meters will it take to stop? b. Repeat for a car going 110 m/s.

17 a. vf 2 = vi 2 + 2 ad d = (vf 2 – vi 2)/2 a = (0 – 552)/(2*-11) = 137 m

17 b. vf 2 = vi 2 + 2 ad d = (vf 2 – vi 2)/2 a = (0 – 1102)/(2*-11) = 550 m

25 a. Determine if the car hits the barrier. d = 50 meters, it hits the barrier 25 b. V = 22 m/s

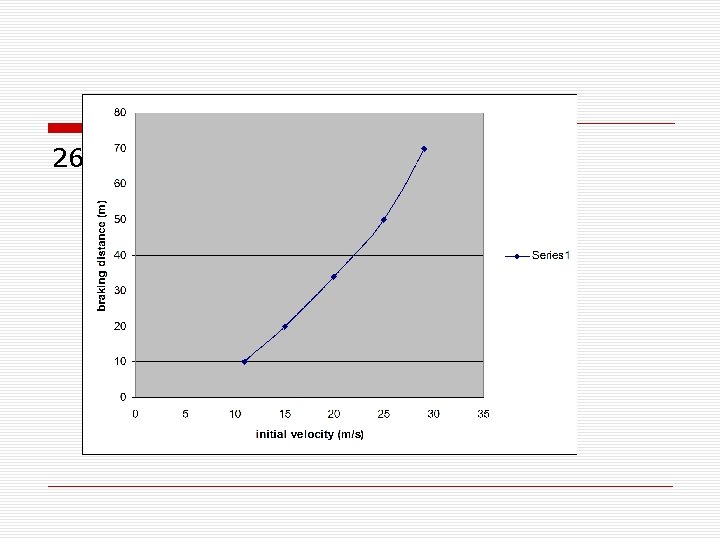
26 a.

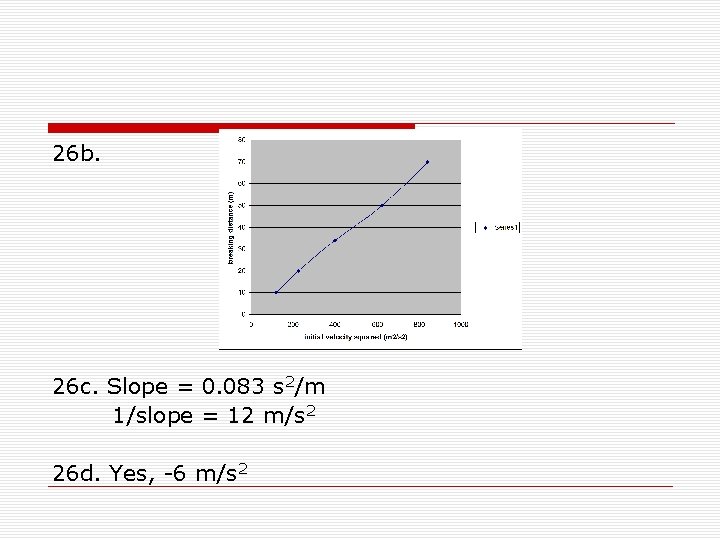
26 b. 26 c. Slope = 0. 083 s 2/m 1/slope = 12 m/s 2 26 d. Yes, -6 m/s 2

28 a. Dcar = 150 meters 28 b. vf = 42 m/s

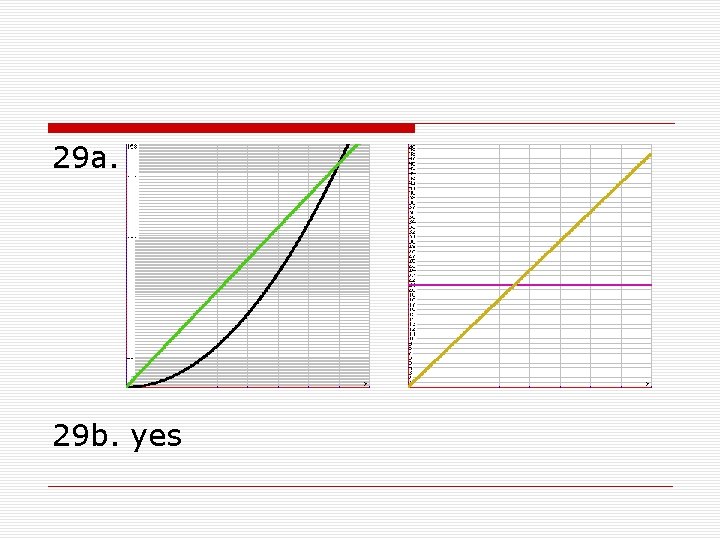
29 a. 29 b. yes

33 a. vf = -15 m/s 33 b. d = -10 m

34 a. vf = -25 m/s 34 b. d = -30 m 34 c. The helicopter has fallen -10 m and the bag is 20 m below the helicopter 34 d. The bag is 20 m below the helicopter after 2 s.