Tangential Centripetal Acceleration Unit 7 2 1 Rotational

Tangential & Centripetal Acceleration Unit 7. 2 1

Rotational Motion Up until now, we have been dealing with linear motion. The next type of motion we will study will be angular or rotational motion. 2

Rotational Motion When an object spins, it is said to undergo rotational motion. In other words rotational motion is the motion of a body that spins about an axis. 3

Rotational Motion A point on an object that rotates about a single axis undergoes circular motion around that axis. In other words, regardless of the shape of the object, any single point on the object travels in a circle around the axis of rotation. 4

Rotational Motion It is difficult to describe the motion of a point moving in a circle using only the linear quantities because the direction of motion in a circular path is constantly changing. 5

Rotational Motion This is why circular motion is described in terms of the angle through which the point on an object moves. 6

Tangential & Centripetal Acceleration The motion of a point on a rotating object is most easily described in terms of an angle from a fixed reference line. 7

Tangential & Centripetal Acceleration In some cases, however, it is useful to understand how the angular speed angular acceleration of a rotating object related to the linear speed and linear acceleration of a point on the object. 8

Tangential & Centripetal Acceleration Imagine an amusement park carousel rotating about its center. Because a carousel is a rigid object, any 2 horses attached to the carousel have the angular speed angular acceleration regardless of their respective distances from the axis of rotation. 9

Tangential & Centripetal Acceleration However, the 2 horses have different tangential speeds. The tangential speed of any point rotating about an axis is also called instantaneous linear speed of that point. 10

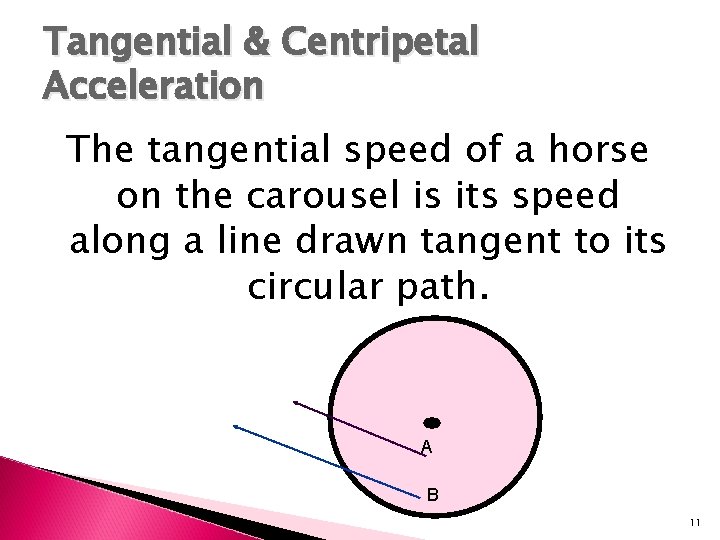
Tangential & Centripetal Acceleration The tangential speed of a horse on the carousel is its speed along a line drawn tangent to its circular path. A B 11

Tangential & Centripetal Acceleration Note that the speed of the horse at point A is represented by a shorter arrow that the 1 that represents the speed of the horse at point B. This reflects the different tangential speeds of the 2 horses. 12

Tangential & Centripetal Acceleration The horse on the outside must travel the same angular displacement during the same amount of time as the horse on the inside. To achieve this, the horse on the outside must travel a greater distance, Δs, then the horse on the inside. 13

Tangential & Centripetal Acceleration Thus the object that is farther from the axis of a rigid rotating body must travel at a higher tangential speed around the circular path, Δs, to travel the same angular displacement as would an object closer to the axis. 14

Tangential & Centripetal Acceleration The angular displacement of the horse is given by the equation Δθ =Δs r 15

Tangential & Centripetal Acceleration To find the tangential speed of the horse, divide both sides of the equation by the times the horse takes to travel the distance Δs Δθ = 1Δs Δt rΔt Tangential speed = vt = rω 16

Tangential & Centripetal Acceleration Note that ω is the instantaneous angular speed rather than the average angular speed because the time interval is so short. 17

Tangential & Centripetal Acceleration This equation is valid only when ω is measured in radians per unit of time. Other measures of angular speed, such as degrees per second and revolution per second must not be used in the equation. 18

Tangential & Centripetal Acceleration If a carousel speeds up, the horse on it experience an angular acceleration. The linear acceleration related to this angular acceleration is tangent to the circular path and is called the tangential acceleration. 19

Tangential & Centripetal Acceleration at = r α the angular acceleration in the equation refers to the instantaneous angular acceleration. SI units expressed as meters per second squared m/s 2 20

Centripetal Acceleration Now think of a car moving in a circular path with a constant speed, it still has acceleration a = vf – v i t f - ti 21

Centripetal Acceleration Note that acceleration depends on a change in velocity. Because velocity is a vector, there are 2 ways an acceleration can be produced by a change in magnitude of velocity or by a change in the direction of the velocity. 22

Centripetal Acceleration For a car moving in a circular path with constant speed, the acceleration is due to a change in direction. An acceleration of this nature is called a centripetal acceleration. 23

Centripetal Acceleration Its magnitude is given by the following equation: a c = v t 2 r tangential speed 2 distance from axis ac = rω2 distance from axis x angular speed 2 24

Centripetal Acceleration Centripetal and tangential acceleration are not the same. The centripetal component of acceleration is due to changing direction. 25

Centripetal Acceleration When both components of acceleration exist simultaneously, the tangential acceleration is tangent to the circular path and the centripetal acceleration toward the center of the circular path. 26

Centripetal Acceleration Because these components of acceleration are perpendicular to each other, the magnitude of the total acceleration can be found using the Pythagorean theorem a total = √[at 2 + ac 2 ] 27