MOTION UNDER CONSTANT ACCELERATION Constant Acceleration Constant acceleration

MOTION UNDER CONSTANT ACCELERATION

Constant Acceleration • Constant acceleration refers to motion where the speed increases by the same amount each second. • The most notable and important example is free fall. • When an object is thrown or dropped, it experiences a constant acceleration due to gravity, which has a constant value of approximately 10 meters per second squared.

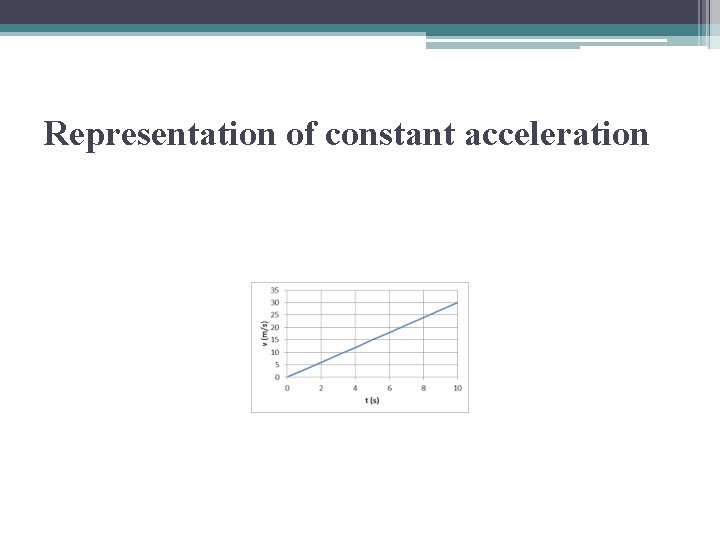
Representation of constant acceleration

Is constant acceleration 0? • Zero acceleration means there is no change in velocity i. e. body is moving with same velocity but constant acceleration means velocity of a body increases or decreases with same rate i. e. by same amount in same time. . so, zero acceleration and constant acceleration are not same…

Motion with constant acceleration • Motion with constant acceleration occurs in everyday life whenever an object is dropped: the object moves downward with the constant acceleration, under the influence of gravity.

What is the equation for motion with constant acceleration? •

What happens at constant acceleration? • An accelerating object will change its velocity by the same amount each second. This is referred to as a constant acceleration since the velocity is changing by a constant amount each second. An object with a constant acceleration should not be confused with an object with a constant velocity.

Kinematic equations for one-dimensional motion with constant acceleration • Let us consider one-dimensional motion in the x-direction. The average acceleration equals the instantaneous acceleration. • From ax = (vxf - vxi)/(tf - ti) • we obtain ax(tf - ti) = (vxf - vxi), • or vxf = vxi + ax∆t. • The velocity versus time graph is a straight line.

Average velocity • The average velocity in a time interval ∆t therefore is just the sum of the final and the initial velocities divided by 2, vx(avg) = (vxf + vxi)/2.

Displacement • The displacement is ∆x = vx(avg)∆t. We can rewrite this expression to obtain xf - xi = ½(vxf + vxi)∆t or xf - xi = vxi∆t + ½ax∆t 2.

Velocity as a function of the displacement • We can also express the velocity as a function of the displacement. yields ∆x = ½(vxf + vxi)∆t = ½ (vxf + vxi)(vxf - vxi)/ax = (vxf 2 - vxi 2)/(2 ax) vxf 2 = vxi 2 + 2 ax(xf - xi). • The equations are the kinematic equations for motion in the xdirection with constant acceleration.