CHAPTER 2 LINEAR TIMEINVARIANT SYSTEMS 2 0 INTRODUCTION



![Example 2. 1 Consider a LTI system with unit sample response h[n] and input Example 2. 1 Consider a LTI system with unit sample response h[n] and input](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-4.jpg)
![x[k] k 012 h[n-k] If n<-2, n-2 k n+2 h[-2 -k] If n= -2, x[k] k 012 h[n-k] If n<-2, n-2 k n+2 h[-2 -k] If n= -2,](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-5.jpg)
![x[k] k 012 h[-1 -k] If n= -1, -3 k 0 1 If n=0, x[k] k 012 h[-1 -k] If n= -1, -3 k 0 1 If n=0,](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-6.jpg)
![x[k] k 012 h[1 -k] If n=1, -1 0 If n=2, 3 k h[2 x[k] k 012 h[1 -k] If n=1, -1 0 If n=2, 3 k h[2](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-7.jpg)
![x[k] k 012 h[3 -k] If n=3, 1 3 k 5 h[4 -k] If x[k] k 012 h[3 -k] If n=3, 1 3 k 5 h[4 -k] If](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-8.jpg)
![h[n-k] If n>4, 0 n-2 n n+2 k y[n] 2. 5 2 1. 5 h[n-k] If n>4, 0 n-2 n n+2 k y[n] 2. 5 2 1. 5](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-9.jpg)
![Example 2. 2 Consider an input x[n] and a unit sample response h[n] given Example 2. 2 Consider an input x[n] and a unit sample response h[n] given](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-10.jpg)
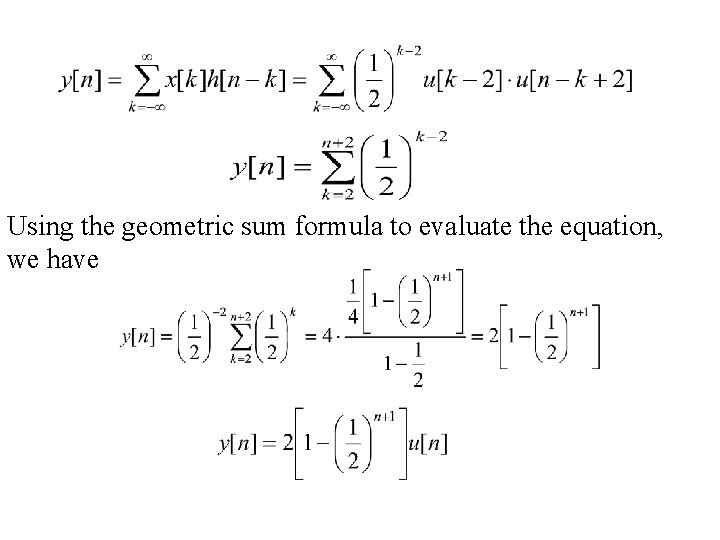
![y[n] 2 1 … … Graph of y[n] in Example 2. 2 n y[n] 2 1 … … Graph of y[n] in Example 2. 2 n](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-12.jpg)






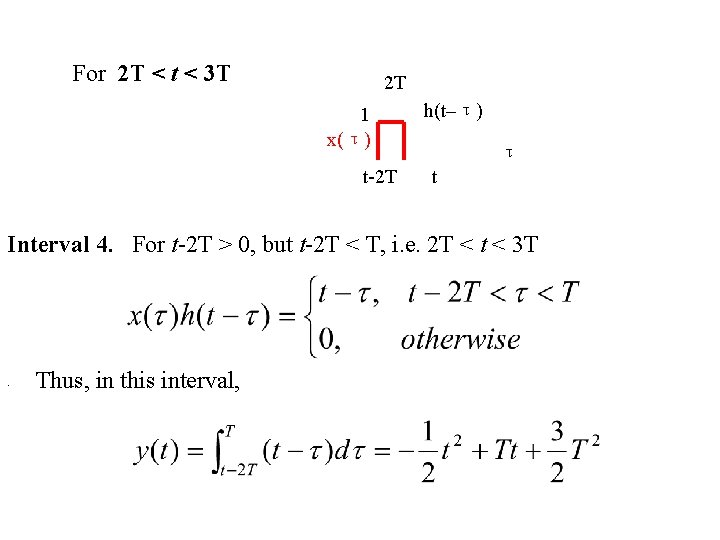














![The solution for the given equation is From the initial condition of y[0]=1, we The solution for the given equation is From the initial condition of y[0]=1, we](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-38.jpg)

![Considering y[n] =0 for n≤ 0, the solution is Considering y[n] =0 for n≤ 0, the solution is](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-40.jpg)


![x[n] b y[n] + D -a y[n-1] Block diagram representation for the causal discrete-time x[n] b y[n] + D -a y[n-1] Block diagram representation for the causal discrete-time](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-43.jpg)

- Slides: 45

CHAPTER 2 LINEAR TIMEINVARIANT SYSTEMS 2. 0 INTRODUCTION • LTI systems possesses the superposition(叠加) property. • Represent signals as linear combinations of delayed impulses. • Convolution sum(卷积和) or convolution integral( 卷积积分). • linear constant-coefficient difference or differential equations (线性常系数差分或微分方 程).

2. 1 DISCRETE-TIME SYSTEMS: THE CONVOLUTION SUM Ø The representation of discrete-time signals in terms of unit samples: Ø Unit sample response h[n] : response of the LTI system to the unit sample δ[n] → h[n] Ø Writing any arbitrary input x[n] as: Øthe response y[n] to x[n] is the weighted linear combination of delayed unit sample responses:

The Convolution Sum Representation of LTI Systems Øconvolution sum or superposition sum : Ø Representing the convolution operation symbolically as: ØLTI system is completely characterized by its response to the unit sample --h[n].
![Example 2 1 Consider a LTI system with unit sample response hn and input Example 2. 1 Consider a LTI system with unit sample response h[n] and input](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-4.jpg)
Example 2. 1 Consider a LTI system with unit sample response h[n] and input x[n], as illustrated in Figure (a). Calculate the convolution sum of these two sequences graphically. x[n] 0 12 h[n] n (a) -2 0 2 x[k] n h[-k] h[2] 012 k (b) h[-2] -2 0 2 k
![xk k 012 hnk If n2 n2 k n2 h2 k If n 2 x[k] k 012 h[n-k] If n<-2, n-2 k n+2 h[-2 -k] If n= -2,](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-5.jpg)
x[k] k 012 h[n-k] If n<-2, n-2 k n+2 h[-2 -k] If n= -2, h[-2] h[2] k -4 -1 0
![xk k 012 h1 k If n 1 3 k 0 1 If n0 x[k] k 012 h[-1 -k] If n= -1, -3 k 0 1 If n=0,](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-6.jpg)
x[k] k 012 h[-1 -k] If n= -1, -3 k 0 1 If n=0, h[-k] -2 0 2 k
![xk k 012 h1 k If n1 1 0 If n2 3 k h2 x[k] k 012 h[1 -k] If n=1, -1 0 If n=2, 3 k h[2](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-7.jpg)
x[k] k 012 h[1 -k] If n=1, -1 0 If n=2, 3 k h[2 k] 0 2 4 k
![xk k 012 h3 k If n3 1 3 k 5 h4 k If x[k] k 012 h[3 -k] If n=3, 1 3 k 5 h[4 -k] If](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-8.jpg)
x[k] k 012 h[3 -k] If n=3, 1 3 k 5 h[4 -k] If n=4, 0 2 3 4 5 6 k
![hnk If n4 0 n2 n n2 k yn 2 5 2 1 5 h[n-k] If n>4, 0 n-2 n n+2 k y[n] 2. 5 2 1. 5](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-9.jpg)
h[n-k] If n>4, 0 n-2 n n+2 k y[n] 2. 5 2 1. 5 0. 5 -2 -1 0 1 2 3 4 Graph of y[n] in Example 2. 1 k
![Example 2 2 Consider an input xn and a unit sample response hn given Example 2. 2 Consider an input x[n] and a unit sample response h[n] given](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-10.jpg)
Example 2. 2 Consider an input x[n] and a unit sample response h[n] given by Determine and plot the output
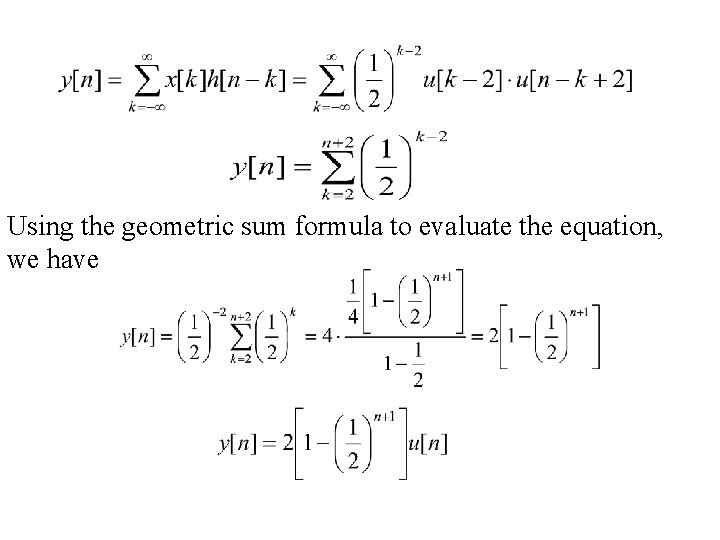
Using the geometric sum formula to evaluate the equation, we have
![yn 2 1 Graph of yn in Example 2 2 n y[n] 2 1 … … Graph of y[n] in Example 2. 2 n](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-12.jpg)
y[n] 2 1 … … Graph of y[n] in Example 2. 2 n

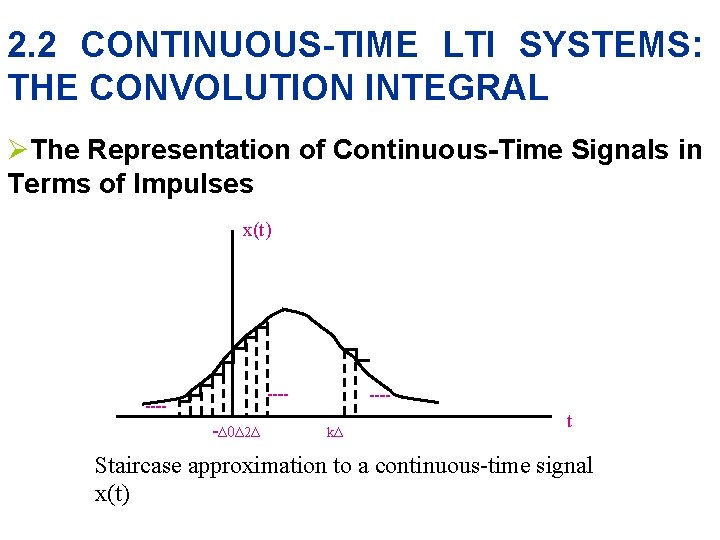
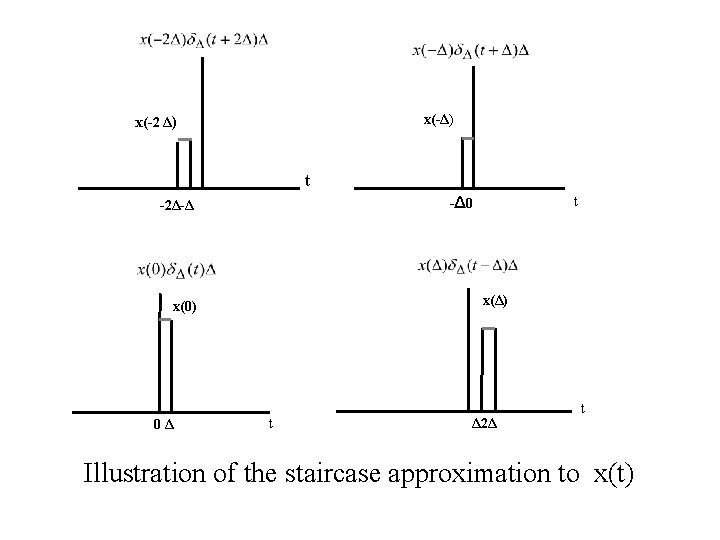
2. 2 CONTINUOUS-TIME LTI SYSTEMS: THE CONVOLUTION INTEGRAL ØThe Representation of Continuous-Time Signals in Terms of Impulses x(t) ┉ ┉ -Δ 0Δ 2Δ ┉ kΔ t Staircase approximation to a continuous-time signal x(t)

x(-Δ) x(-2 Δ) t x(Δ) x(0) 0Δ t -Δ 0 -2Δ-Δ t Δ 2Δ t Illustration of the staircase approximation to x(t)

as , the summing approaches an integral and the unit impulse function Compared with the Sampling property of the unit impulse: +¥ x(t 0 ) = ò-¥ x(t )d (t - t 0 )dt is

ØThe Continuous-Time Unit Impulse Response(单位冲 激响应) and the Convolution Integral Representation of LTI Systems: Give the as the response of a continuous-time LTI system to the input , then the response of the system to pulse is Thus, the response As to is , in addition, the summing becomes an integral. Therefore, Øconvolution integral or the superposition integral :

Øunit impulse response h(t) : the response to the input . ØRepresent convolution integral of two signals x(t) and h(t) symbolically as: ØA continuous-time LTI system is completely characterized by its unit impulse response h(t). Example 2. 3 Consider the convolution of the following two signals, which are depicted in (a): x(t) h(t) 2 T 1 0 T t (a) 0 2 T t

From the definition of the convolution integral of two continuous-time signals, For t < 0 h(t–τ) 2 T 1 x(τ) τ t-2 T t 0 T . Interval 1. For t < 0, there is no overlap between the nonzero portions of and , and consequently,

For 0 < t < T h(t–τ) t-2 T Interval 2. For 0 < t < T, . Thus, in this interval, . 2 T 1 0 t. T x(τ) τ

For T < t < 2 T h(t–τ) 2 T 1 x(τ) τ t-2 T T t Interval 3. For t > T but t-2 T < 0, i. e. T < t <2 T Thus, in this interval,
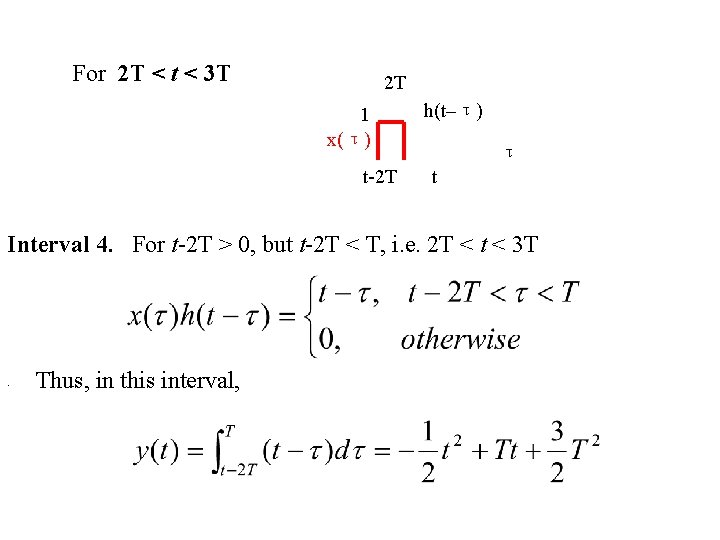
For 2 T < t < 3 T 2 T 1 x(τ) t-2 T h(t–τ) τ t Interval 4. For t-2 T > 0, but t-2 T < T, i. e. 2 T < t < 3 T . Thus, in this interval,

For t > 3 T 1 x(τ) 2 T 0 T t-2 T h(t–τ) τ t Interval 4. For t-2 T > T, or equivalently, t > 3 T, there is no overlap and , and hence, between the nonzero portions of Summarizing,

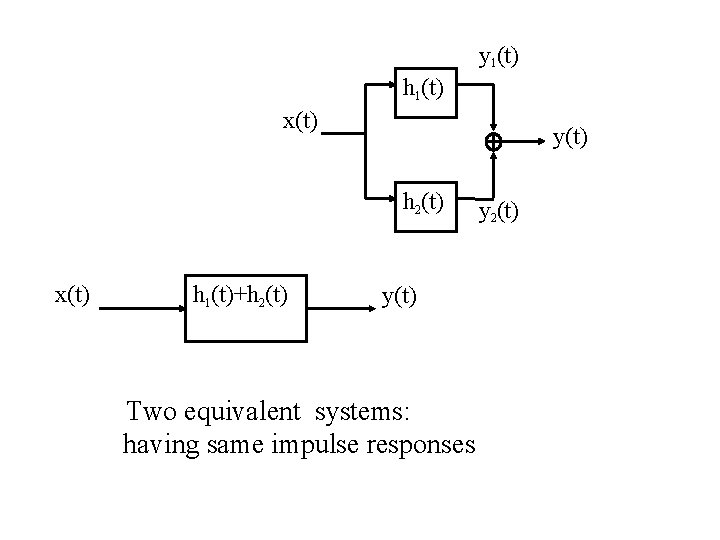
2. 3 PROPERTIES OF INVARIANT SYSTEMS LINEAR 2. 3. 1 The Commutative Property(交换律) in discrete time : in continuous time: 2. 3. 2 The Distributive Property (分配律) in discrete time : in continuous time: TIME-

y 1(t) h 1(t) x(t) y(t) h 2(t) x(t) h 1(t)+h 2(t) y(t) Two equivalent systems: having same impulse responses y 2(t)

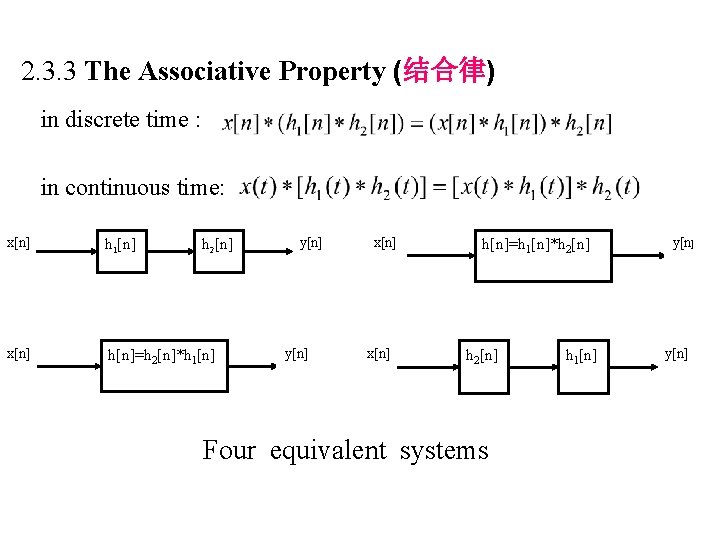
2. 3. 3 The Associative Property (结合律) in discrete time : in continuous time: x[n] h 1[n] x[n] h[n]=h 2[n]*h 1[n] h 2[n] y[n] x[n] h[n]=h 1[n]*h 2[n] Four equivalent systems h 1[n] y[n]

2. 3. 4 LTI Systems with and without Memory for a discrete-time LTI system without memory: for a continuous-time LTI system without memory: 2. 3. 5 Invertibility of LTI Systems The impulse responses of a system and its inverse system satisfy the following condition: in discrete-time : in continuous-time: Since

2. 3. 6 Causality for LTI Systems for a causal discrete-time LTI system: for a causal continuous-time LTI system: 2. 3. 7 Stability for LTI Systems for a stable discrete-time LTI system: for a stable continuous-time LTI system: absolutely summable absolutely integrable

2. 3. 8 The Unit Step Response(单位阶跃响应) of an LTI System ØThe unit step response, s[n] or s(t), is the output of an LTI system when input x[n]=u[n] or x(t)=u(t). ØThe unit step response of a discrete-time LTI system is the running sum of its sample response: ØThe unit sample response of a discrete-time LTI system is the first difference of its step response:

ØThe unit step response of a continuous-time LTI system is the running integral of its impulse response: ØThe unit impulse response of a continuous-time LTI system is the first derivative of the unit step response : ØProperties of convolution integral: Derivative property: Integral property: Combining the two properties, we have

2. 4 CAUSAL LTI SYSTEMS DESCRIBED BY DIFFERENTIAL AND DIFFERENCE EQUATIONS R Example 2. 4 : input signal; Vs : output signal. + – i (t) C Linear constant-coefficient differential equation

ØLinear constant-coefficient differential equation is the mathematical representation of a continuous-time LTI system. ØLinear constant-coefficient difference equation is the mathematical representation of a discrete-time LTI system. §Linear constant-coefficient differential(difference) equation provides an implicit relationship between the input and output rather than an explicit expression for the system output as a function of the input. §We must specify one or more auxiliary conditions to solve a differential (difference) equation. • Initial rest(初始静止): for a causal LTI system, if x(t)=0 for t<t 0, then y(t) must also equal 0 for t<t 0.

forced response (受迫响应) natural response (自然响应) • It is important to emphasize that the condition of initial rest does not specify a zero initial condition at a fixed point in time, but rather adjusts this point in time so that the response is zero until the input becomes nonzero. Thus, if x(t)=0 for t≤t 0 for a causal LTI system, then y(t)=0 for t≤ t 0, and we would use the initial condition y(t 0)=0 to solve for the output for t> t 0.

• General Nth-order linear constant-coefficient differential equation: N auxiliary conditions:

In Example 2. 4, If R=4, C=1/2, and the input signal is Then we obtain From the eigenvalue of the homogeneous equation, we can write Since for t>0, so let Taking x(t) and for t >0 into the original equation yields Thus So the solution of the differential equation for t>0 is

Taking use of the condition – initial rest, we obtain Consequently, for t>0 or

• General Nth-order linear constant-coefficient difference equation: üFirst resolution: N auxiliary conditions: üSecond resolution: (recursive method(迭 代方法))

Example 2. 5 Solve the difference equation The eigen equation is So the eigenvalue is a= – 2 We can write Let Taking Thus into the original equation yields and y[0]=1.
![The solution for the given equation is From the initial condition of y01 we The solution for the given equation is From the initial condition of y[0]=1, we](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-38.jpg)
The solution for the given equation is From the initial condition of y[0]=1, we have Consequently,

Example 2. 6 Consider the difference equation Determine the output recursively with the condition of initial rest and Rewrite the given difference equation as . Starting from initial condition, we can solve for successive values of y[n] for n≥ 1:
![Considering yn 0 for n 0 the solution is Considering y[n] =0 for n≤ 0, the solution is](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-40.jpg)
Considering y[n] =0 for n≤ 0, the solution is

What are the relationships between yp, yh, yzi and yzs ?

2. 5 Block Diagram Representations of First. Order Systems Described by Differential and Difference Equations §First-order difference equation : addition delay multiplication §Three basic elements in block diagram: adder, multiplier and delayer. (方框图) (加法器)(乘法器) (延时器) a x 2[n] x[n] ax[n] (b) x 1[n] + (a) x 1[n]+x 2[n] x[n] D x[n-1] (c) Basic elements for the block diagram representation of causal discrete-time systems. (a) an adder; (b) a multiplier; (c) a delayer.
![xn b yn D a yn1 Block diagram representation for the causal discretetime x[n] b y[n] + D -a y[n-1] Block diagram representation for the causal discrete-time](https://slidetodoc.com/presentation_image_h2/4b23f23d936bd5cdbd752cdcca0185ae/image-43.jpg)
x[n] b y[n] + D -a y[n-1] Block diagram representation for the causal discrete-time system described by the first-order difference equation (y[n]+ay[n-1]=bx[n]). §First-order differential equation : differentiation

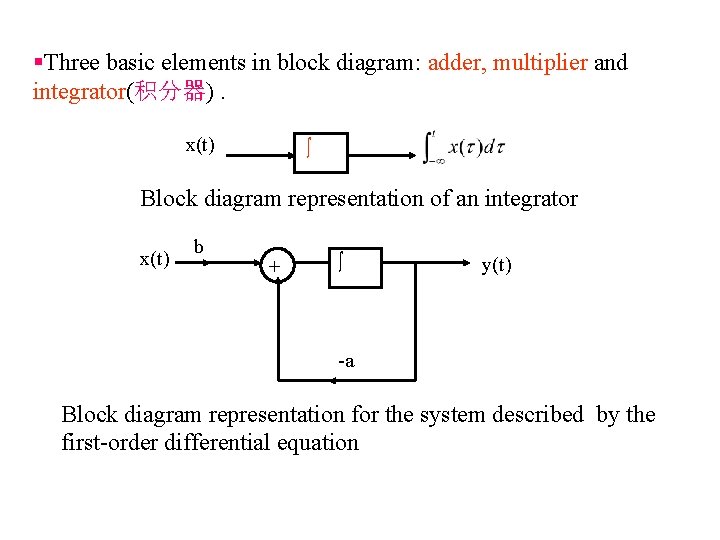
§Three basic elements in block diagram: adder, multiplier and integrator(积分器). x(t) ∫ Block diagram representation of an integrator x(t) b + ∫ y(t) -a Block diagram representation for the system described by the first-order differential equation

2. 6 SUMMARY ØA representation of an arbitrary discrete-time signal as weighted sums of shifted unit samples; ØConvolution sum representation for the response of a discrete-time LTI systems; ØA representation of an arbitrary continuous-time signal a weighted integrals of shifted unit impulses; ØConvolution integral representation for continuous-time LTI systems; ØRelating LTI system properties, including causality, stability, to corresponding properties of the unit impulse (sample) response; ØSome of the properties of systems described by linear constant-coefficient differential (difference) equations; ØUnderstanding of the condition of initial rest.
 Chapter 1 systems of linear equations and matrices
Chapter 1 systems of linear equations and matrices Levels of ecological organization
Levels of ecological organization Chapter 1 ems systems
Chapter 1 ems systems Simple linear regression and multiple regression
Simple linear regression and multiple regression Contoh soal persamaan non linear
Contoh soal persamaan non linear Types of non linear text
Types of non linear text Linear plot structure
Linear plot structure Contoh soal metode numerik iterasi
Contoh soal metode numerik iterasi Non linear pipeline processor
Non linear pipeline processor What is linear multimedia
What is linear multimedia Left linear to right linear grammar
Left linear to right linear grammar Fungsi linear dan non linear
Fungsi linear dan non linear Pengertian fungsi linear dan non linear
Pengertian fungsi linear dan non linear Conditions for linear independence
Conditions for linear independence Linear algebra linear transformation
Linear algebra linear transformation Rumus koordinat lereng
Rumus koordinat lereng Linear impulse and momentum
Linear impulse and momentum Contoh soal persamaan simultan
Contoh soal persamaan simultan Nonlinear tables
Nonlinear tables Table linear or nonlinear
Table linear or nonlinear Difference between linear and non linear equations
Difference between linear and non linear equations Linear and nonlinear editing
Linear and nonlinear editing Sistem persamaan linear metode numerik
Sistem persamaan linear metode numerik Closure properties of regular languages
Closure properties of regular languages Tipos de narrador de texto
Tipos de narrador de texto Solving systems of linear inequalities by graphing
Solving systems of linear inequalities by graphing Simple linear equations word problems
Simple linear equations word problems Inequalities warm up
Inequalities warm up System of equations
System of equations Solving linear equations calculator
Solving linear equations calculator Solving linear systems by graphing lesson 11-1
Solving linear systems by graphing lesson 11-1 Systems of linear equations real world applications
Systems of linear equations real world applications Graphing linear-quadratic systems
Graphing linear-quadratic systems 6-1 multivariable linear systems and row operations
6-1 multivariable linear systems and row operations Nonhomogeneous linear system
Nonhomogeneous linear system Lesson 9.1 solving linear systems by graphing answer key
Lesson 9.1 solving linear systems by graphing answer key Lesson 3 linear equations in x
Lesson 3 linear equations in x Direct methods for sparse matrices
Direct methods for sparse matrices 6-6 systems of linear inequalities
6-6 systems of linear inequalities Systems of inequalities quiz part one
Systems of inequalities quiz part one 6-6 systems of linear inequalities
6-6 systems of linear inequalities Special systems of equations
Special systems of equations Solve systems of linear inequalities by graphing calculator
Solve systems of linear inequalities by graphing calculator How to solve linear quadratic systems algebraically
How to solve linear quadratic systems algebraically Linear systems unit test part 2
Linear systems unit test part 2 Inequalities word problems
Inequalities word problems