Linear Systems Systems of Linear Equations Solving Systems

























































- Slides: 64

Linear Systems • Systems of Linear Equations • Solving Systems of Equations by Substitution 1

Systems of Equations A set of equations is called a system of equations. The solutions must satisfy each equation in the system. If all equations in a system are linear, the system is a system of linear equations, or a linear system.

Systems of Linear Equations: A solution to a system of equations is an ordered pair that satisfy all the equations in the system. A system of linear equations can have: 1. Exactly one solution 2. No solutions 3. Infinitely many solutions 3

Systems of Linear Equations: There are four ways to solve systems of linear equations: 1. By graphing 2. By substitution 3. By addition (also called elimination) 4. By multiplication 4

Solving Systems by Graphing: When solving a system by graphing: 1. Find ordered pairs that satisfy each of the equations. 2. Plot the ordered pairs and sketch the graphs of both equations on the same axis. 3. The coordinates of the point or points of intersection of the graphs are the solution or solutions to the system of equations. 5

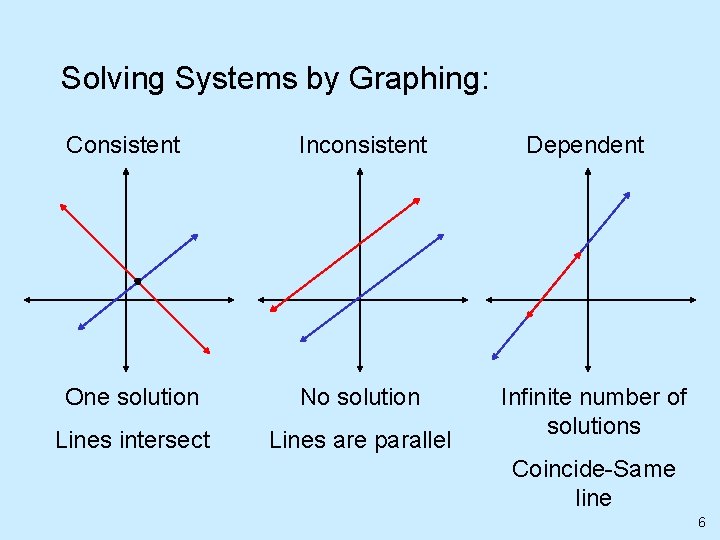
Solving Systems by Graphing: Consistent Inconsistent One solution No solution Lines intersect Lines are parallel Dependent Infinite number of solutions Coincide-Same line 6

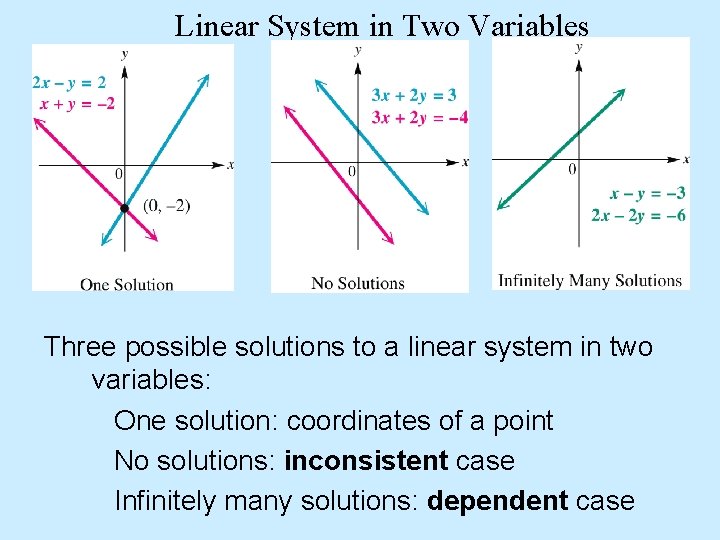
Linear System in Two Variables Three possible solutions to a linear system in two variables: One solution: coordinates of a point No solutions: inconsistent case Infinitely many solutions: dependent case

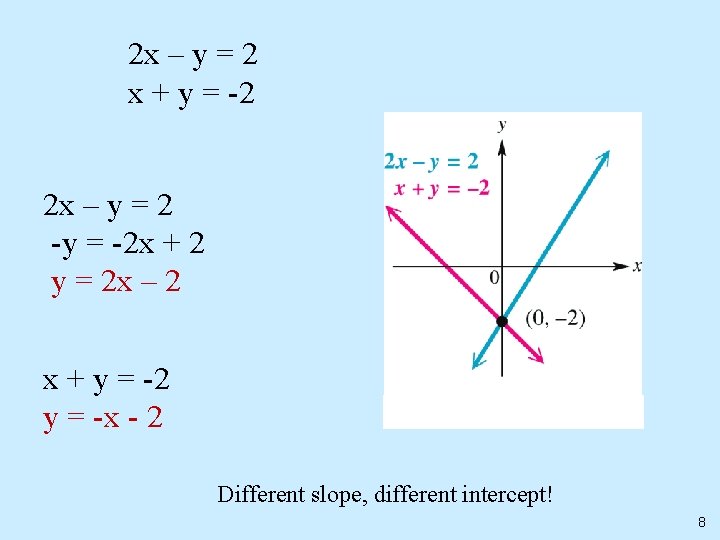
2 x – y = 2 x + y = -2 2 x – y = 2 -y = -2 x + 2 y = 2 x – 2 x + y = -2 y = -x - 2 Different slope, different intercept! 8

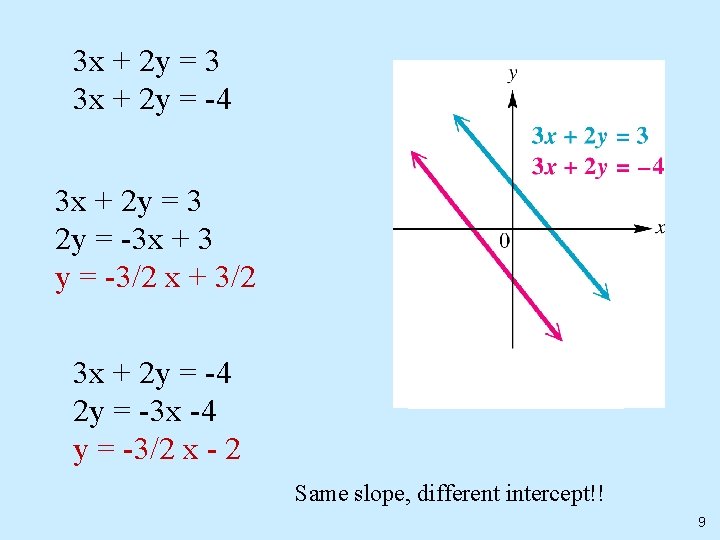
3 x + 2 y = 3 3 x + 2 y = -4 3 x + 2 y = 3 2 y = -3 x + 3 y = -3/2 x + 3/2 3 x + 2 y = -4 2 y = -3 x -4 y = -3/2 x - 2 Same slope, different intercept!! 9

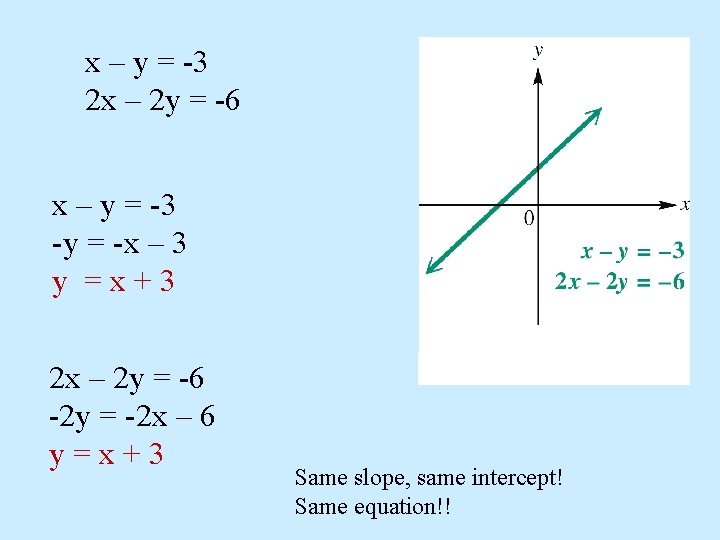
x – y = -3 2 x – 2 y = -6 x – y = -3 -y = -x – 3 y =x+3 2 x – 2 y = -6 -2 y = -2 x – 6 y=x+3 Same slope, same intercept! Same equation!!

Determine Without Graphing: • There is a somewhat shortened way to determine what type (one solution, no solutions, infinitely many solutions) of solution exists within a system. • Notice we are not finding the solution, just what type of solution. • Write the equations in slope-intercept form: y = mx + b. (i. e. , solve the equations for y, remember that m = slope, b = y - intercept). 11

Determine Without Graphing: Once the equations are in slope-intercept form, compare the slopes and intercepts. One solution – the lines will have different slopes. No solution – the lines will have the same slope, but different intercepts. Infinitely many solutions – the lines will have the same slope and the same intercept. 12

Determine Without Graphing: Given the following lines, determine what type of solution exists, without graphing. Equation 1: 3 x = 6 y + 5 Equation 2: y = (1/2)x – 3 Writing each in slope-intercept form (solve for y) Equation 1: y = (1/2)x – 5/6 Equation 2: y = (1/2)x – 3 Since the lines have the same slope but different y-intercepts, there is no solution to the system of equations. The lines are parallel. 13

Substitution Method: Procedure for Substitution Method 1. Solve one of the equations for one of the variables. 2. Substitute the expression found in step 1 into the other equation. 3. Now solve for the remaining variable. 4. Substitute the value from step 2 into the equation written in step 1, and solve for the remaining variable.

Substitution Method: 1. Solve the following system of equations by substitution. Step 1 is already completed. Step 2: Substitute x+3 into 2 nd equation and solve. Step 3: Substitute – 4 into 1 st equation and solve. The answer: ( -4 , -1)

1) Solve the system using substitution Step 1: Solve an equation for one variable. Step 2: Substitute Step 3: Solve the equation. x+y=5 y=3+x The second equation is already solved for y! x+y=5 x + (3 + x) = 5 2 x + 3 = 5 2 x = 2 x=1

1) Solve the system using substitution x+y=5 y=3+x Step 4: Plug back in to find the other variable. Step 5: Check your solution. x+y=5 (1) + y = 5 y=4 (1, 4) (1) + (4) = 5 (4) = 3 + (1) The solution is (1, 4). What do you think the answer would be if you graphed the two equations?

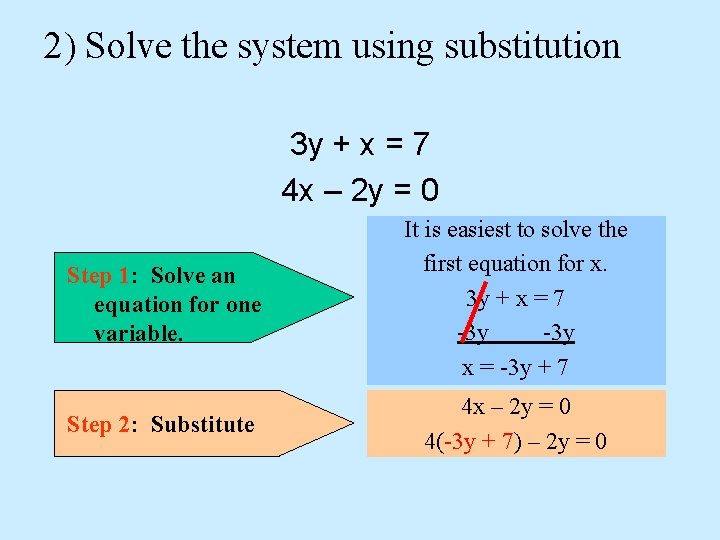
2) Solve the system using substitution 3 y + x = 7 4 x – 2 y = 0 Step 1: Solve an equation for one variable. It is easiest to solve the first equation for x. 3 y + x = 7 -3 y x = -3 y + 7 Step 2: Substitute 4 x – 2 y = 0 4(-3 y + 7) – 2 y = 0

2) Solve the system using substitution 3 y + x = 7 4 x – 2 y = 0 Step 3: Solve the equation. Step 4: Plug back in to find the other variable. -12 y + 28 – 2 y = 0 -14 y + 28 = 0 -14 y = -28 y=2 4 x – 2 y = 0 4 x – 2(2) = 0 4 x – 4 = 0 4 x = 4 x=1

2) Solve the system using substitution 3 y + x = 7 4 x – 2 y = 0 Step 5: Check your solution. (1, 2) 3(2) + (1) = 7 4(1) – 2(2) = 0

Deciding whether an ordered pair is a solution of a linear system. The solution set of a linear system of equations contains all ordered pairs that satisfy all the equations at the same time. Example 1: Is the ordered pair a solution of the given system? 2 x + y = -6 Substitute the ordered pair into each equation. x + 3 y = 2 Both equations must be satisfied. A) (-4, 2) B) (3, -12) 2(-4) + 2 = -6 2(3) + (-12) = -6 (-4) + 3(2) = 2 (3) + 3(-12) = 2 -6 = -6 2=2 -33 -6 Yes No

Substitution Method Example Solve the system. (1) (2) Solution Solve (2) for y. Substitute y = x + 3 in (1). Solve for x. Substitute x = 1 in y = x + 3. Solution set: {(1, 4)}

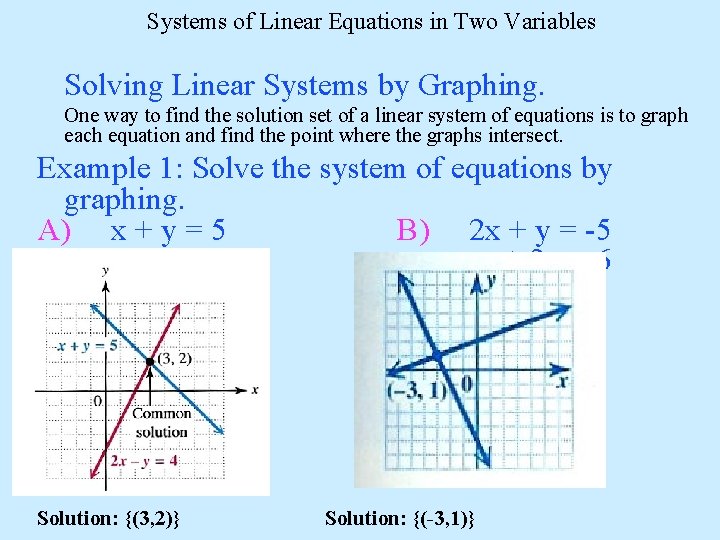
Systems of Linear Equations in Two Variables Solving Linear Systems by Graphing. One way to find the solution set of a linear system of equations is to graph each equation and find the point where the graphs intersect. Example 1: Solve the system of equations by graphing. A) x + y = 5 B) 2 x + y = -5 2 x - y = 4 -x + 3 y = 6 Solution: {(3, 2)} Solution: {(-3, 1)}

Systems of Linear Equations in Two Variables Solving Linear Systems by Graphing. There are three possible solutions to a system of linear equations in two variables that have been graphed: 1) The two graphs intersect at a single point. The coordinates give the solution of the system. In this case, the solution is “consistent” and the equations are “independent”. 2) The graphs are parallel lines. (Slopes are equal) In this case the system is “inconsistent” and the solution set is 0 or null. 3) The graphs are the same line. (Slopes and y-intercepts are the same) In this case, the equations are “dependent” and the solution set is an infinite set of ordered pairs.

4 -1 Systems of Linear Equations in Two Variables Solving Linear Systems of two variables by Method of Substitution. Step 1: Solve one of the equations for either variable Step 2: Substitute for that variable in the other equation (The result should be an equation with just one variable) Step 3: Solve the equation from step 2 Step 4: Substitute the result of Step 3 into either of the original equations and solve for the other value. Step 6: Check the solution and write the solution set.

4 -1 Systems of Linear Equations in Two Variables Solving Linear Systems of two variables by Method of Substitution. Example 6: Solve the system : 4 x + y = 5 2 x - 3 y =13 Step 1: Choose the variable y to solve for in the top equation: y = -4 x + 5 Step 2: Substitute this variable into the bottom equation 2 x - 3(-4 x + 5) = 13 2 x + 12 x - 15 = 13 Step 3: Solve the equation formed in step 2 14 x = 28 x=2 Step 4: Substitute the result of Step 3 into either of the original equations and solve for the other value. 4(2) + y = 5 y = -3 Solution Set: {(2, -3)} Step 5: Check the solution and write the solution set.

Systems of Linear Equations in Two Variables Solving Linear Systems of two variables by Method of Substitution. Example 7: Solve the system : y = -2 x + 2 -2 x + 5(-2 x + 2) = 22 -12 x = 12 x = -1 Solution Set: {(-1, 4)} -2 x - 10 x + 10 = 22 2(-1) + y = 2 y=4

Your Turn: 3 x – y = 4 x = 4 y - 17

Your Turn: 2 x + 4 y = 4 3 x + 2 y = 22

Clearing Fractions or Decimals

Systems without a Single Point Solution

0 = 4 untrue Inconsistent Systems - how can you tell? An inconsistent system has no solutions. (parallel lines) Substitution Technique

0 = 0 or n = n Dependent Systems – how can you tell? A dependent system has infinitely many solutions. (it’s the same line!) Substitution Technique

34

Modeling Examples: The reason to learn about systems of equations is to learn how to solve real world problems. Study Example 8 on page 360 in the text. Notice how the original equations are set up based on the data in the question. Also note that we are trying to determine when the total cost at each garage will be the same. To do this, set the two cost equations equal to each other and solve. You will see this type of problem often. 35

Modeling Examples: Study Example 9 on page 361 in the text. This is a mixture problem. Notice how the original equations are set up based on the data in the question. Once the equations are set up, the 2 nd equation is multiplied by 100 to remove the decimal. This is a common occurrence, so make sure you know how to do this. Note: The example is solved using the addition method. It can also be solved by substitution. 36

Modeling Examples: 4. Read problem 40 on page 362 of the text – “basketball game”. 37

Modeling Examples: 4. Read problem 40 on page 362 of the text – “basketball game”. First assign the variables: let x = # of 2 point shots let y = # of 3 point shots 38

Modeling Examples: 4. Read problem 40 on page 362 of the text – “basketball game”. First assign the variables: let x = # of 2 point shots let y = # of 3 point shots Writing the 1 st equation: They made 45 goals in a recent game x + y = 45 39

Modeling Examples: 4 continued. Writing the 2 nd equation: 40

Modeling Examples: 4 continued. Writing the 2 nd equation: Some 2 pointers, some 3 pointers, for a total score of 101 points 2 x + 3 y = 101 41

Modeling Examples: 4 continued. Writing the 2 nd equation: Some 2 pointers, some 3 pointers, for a total score of 101 points 2 x + 3 y = 101 In words, the equation says 2 times the number of 2 point shots plus 3 times the number of 3 point shots totals 101 points. 42

Modeling Examples: 4 continued. The two equations are: x + y = 45 2 x + 3 y = 101 43

Modeling Examples: 4 continued. The two equations are: -2( x + y = 45 ) Lets eliminate x, multiply the st equation by – 2. entire 1 2 x + 3 y = 101 44

Modeling Examples: 4 continued. The two equations are: -2( x + y = 45 ) Lets eliminate x, multiply the st equation by – 2. entire 1 2 x + 3 y = 101 -2 x + -2 y = -90 2 x + 3 y = 101 45

Modeling Examples: 4 continued. The two equations are: -2( x + y = 45 ) 2 x + 3 y = 101 -2 x + -2 y = -90 2 x + 3 y = 101 y = 11 Add down to eliminate x. Substitute y into the 1 st equation. x + 11 = 45, so x = 34. 34 - 2 point shots and 11 - 3 point shots. 46

Modeling Examples: 5. Read problem 44 on page 363 in the text – A Milk Mixture. 47

Modeling Examples: 5. Read problem 44 on page 363 in the text – A Milk Mixture. First assign the variables: let x = # gallons of 5% milk let y = # gallons of skim (0%) milk 48

Modeling Examples: 5. Read problem 44 on page 363 in the text – A Milk Mixture. First assign the variables: let x = # gallons of 5% milk let y = # gallons of skim (0%) milk Writing the 1 st equation: x + y = 100 This is because they want to make a mixture totaling 100 gallons of milk. 49

Modeling Examples: 5. Continued Writing the 2 nd equation: 50

Modeling Examples: 5. Continued Writing the 2 nd equation: 0. 05 x + 0. 0 y = 0. 035(100) Basically, we are multiplying the 1 st equation by the percent butterfat of the milk. Our final mixture should be 3. 5%, so we multiply 0. 035(100), since we want 100 total gallons. 51

Modeling Examples: 5. Continued The two equations are: x+ y = 100 0. 05 x + 0. 0 y = 0. 035(100) 52

Modeling Examples: 5. Continued The two equations are: x+ y = 100 0. 05 x + 0. 0 y = 0. 035(100) Next, multiply the 2 nd equation by 1000 to remove the decimal. This gives us the following system of equations: x + y = 100 50 x + 0 y = 35(100) 53

Modeling Examples: 5. Continued The two equations are: x+ y = 100 0. 05 x + 0. 0 y = 0. 035(100) Next, multiply the 2 nd equation by 1000 to remove the decimal. This gives us the following system of equations: x + y = 100 50 x + 0 y = 35(100) Solve the system (use substitution since the 2 nd equation has only one variable). The answer follows on the next slide. 54

Modeling Examples: 5. Continued The answer is 70 gallons of 5% milk and 30 gallons of skim (0%) milk. 55

Modeling Examples: 6. Read problem 48 on page 363 in the text – School Play Tickets. 56

Modeling Examples: 6. Read problem 48 on page 363 in the text – School Play Tickets. First assign the variables: let x = # of adult tickets sold ($5 per ticket) let y = # of student tickets sold ($2 per ticket) 57

Modeling Examples: 6. Read problem 48 on page 363 in the text – School Play Tickets. First assign the variables: let x = # of adult tickets sold ($5 per ticket) let y = # of student tickets sold ($2 per ticket) Writing the 1 st equation: x + y = 250 Since a total of 250 tickets were sold. 58

Modeling Examples: 6. Continued Writing the 2 nd equation: 59

Modeling Examples: 6. Continued Writing the 2 nd equation: 5 x + 2 y = 950 Basically, we multiplied the 1 st equation by the price of the tickets, and set it equal to the amount of money collected. 60

Modeling Examples: 6. Continued Writing the 2 nd equation: 5 x + 2 y = 950 Basically, we multiplied the 1 st equation by the price of the tickets, and set it equal to the amount of money collected. Do you see how this is similar to example #4? The 2 and 3 point shots? 61

Modeling Examples: 6. Continued The two equations are: x + y = 250 5 x + 2 y = 950 62

Modeling Examples: 6. Continued The two equations are: x + y = 250 5 x + 2 y = 950 Can you solve the system using either substitution or addition? The answer follows on the next slide. 63

Modeling Examples: 6. Continued The answer is 150 adult tickets were sold, and 100 student tickets were sold. 64