FrequencyDependent TimeInvariant DCDC Converter Modeling without Averaging Patrick








































- Slides: 48

Frequency-Dependent, Time-Invariant DC-DC Converter Modeling without Averaging Patrick Chapman Asst. Prof. UIUC April 10, 2006 Grainger Center for Electric Machines and Electromechanics

Summary l l 2 Overview time-invariant (TI) converter modeling Propose alternative method of TI modeling, avoiding formal averaging Explore simulation results Probe small-signal analysis improvements Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Converter Modeling l DC-DC converter difficulties – – – l Longstanding modeling desires: – – 3 Nonlinear Time-varying Switched Easy control design Rapid simulation Accuracy No “hand-waving” Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Conventional Approach: Averaging l Method dates from 70’s – – – l l Can be done on schematic (circuit-based) Can be done on equations (“state-space”) – 4 Needed way to apply linear control design Needed time-invariant model for this Stability was main priority (fast response, less so) Methods produce equivalent models Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Conventional State-Space Avg. l Often cast in the “timewindow” approach – – l Sometimes cast as weighted average of state matrices – – l 5 T is the switching period x is any time-domain variable d is duty cycle in period T n is integer Methods produce same model Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Synopsis: Conventional Avg. l l l Removes time-varying state matrices Removes switching ripple Models often linearized – – l Calls into question bandwidth limitation – – l 6 Enables small-signal, linear analysis Very widely used What disturbance frequency is valid? Aliasing-like effects neglected Can improperly track the average! Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Tracking Issues in Avg. Models l Occurs in certain converters – l l Occurs even under ideal circuits with modest ripple Two main causes – – 7 Boost and buck-boost in particular Neglecting ripple, ESR in steady-state derivations Sampling effects in feedback control Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Regarding Moving Time-Window l Averaging integral – – – l Imposing questionable – – 8 Relies on continuous time history Can’t be implemented directly in hardware Can complicate rigorous analysis is q is switching signal d is duty cycle command Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

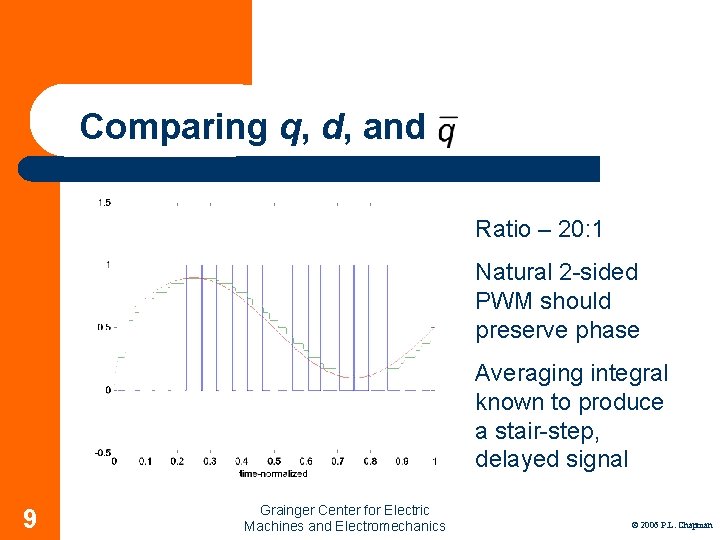
Comparing q, d, and Ratio – 20: 1 Natural 2 -sided PWM should preserve phase Averaging integral known to produce a stair-step, delayed signal 9 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Improvements to Conv. Avg. l Higher order abstractions, ripple estimates – – l Modification of output equation to catch ripple – l l l Lehman (2004) Stability and convergence analysis (Tadmor) These approaches, among others, did much to strengthen and extend averaging Many other improvements and adaptations made – 10 Krein, Bass, et al (“KBM” formality) Sanders, Verghese, Caliskan, Stankovic (“generalized” or “multi-frequency”) Discontinuous mode, other converters, correction factors, etc. Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Multi-Frequency Averaging (MFA) l 11 Accounts for ripple and switching frequency ***Also “Generalized” averaging l Uses higher-order averages l Has implicit assumption of slowly-varying states (at least during time window) Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Perhaps Redefine MFA *Make these definitions Then… 12 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Multiple Reference Frames (MRF) l Quite similar to MFA – – l E. g. , PM motor with nonsinusoidal back EMF – – 13 In context of motor drives (Sudhoff) Multi-phase systems Involves a time-window average w. r. t. rotor position, not time Makes a time-invariant model linear analysis of motor drives Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

PM Motor MRF Analysis *MRF theory, then, has similar properties as MFA 14 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Floquet Theory l l A linear transformation of states Applies to models: – – l l l Produces exact time-invariant model Applied by Visser to open-loop buck, boost Difficult, maybe infeasible, for closed-loop – – 15 Linear Periodic coefficients Closed-loop not periodic Nonlinear theory recent, but doesn’t address aperiodicity Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Questions: l l Can averaging be avoided? If so, – – l Can they be extended? – – 16 Are resulting models “better”? Is rigorous analysis (error bounds) easier? Aliasing-like effects Digital control Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Alternative Approach l l 17 Decompose signal along the lines of MFA – Quasi-Fourier-Series (QFS) components – 2 N+1 variables, a cosine, b sine New variables not defined yet – just notational Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Signal Derivatives (2 nd order, e. g. ) 18 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Switching Function Model - d is the duty cycle - f is the initial phase shift (usually arbitrary) Can let d be a function of time (so long as between 0, 1) 19 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Duty Cycle Ripple l l Usually neglected Usually small – – – l l Current-mode control known to exhibit rippledependent behavior Usually suffices to model one harmonic – 20 Ripple in voltage or current may be fed back Important in proportional control Some filtering may be applied Analysis here is general, but specific N = 1 example given Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Obtaining d and f l Duty cycle command (d) and d not the same Sawtooth: Triangle: 21 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Obtaining d and f l l Times th and tl would occur if QFS variables remained the same until intersection Variables change between switching edges – – l 22 At first seems suspect Cancels out in the infinite sum Necessary step to put in terms of new states Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Switching Function Summary l QFS coefficients: l Solution to transcendental equation – – 23 Inconvenient, but actually quite easy Can use noniterative approximations Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Product Terms l Commonly we have qx – product of switching function and continuous variable l Generates higher order harmonics – – 24 Approximation is the neglect of these Though, can include in “extra” state eqns if desired Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Product Terms, cont’d l l Brute-force calculation (preferred here) Discrete convolution – Use complex exponential QFS for concise statement 2 nd order example 25 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Converter Model l Boost converter example – 26 Tools in place apply to state equations Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Synthesizing Model l l Thus far, we’ve not completely defined variables After making substitutions – – l 27 Can equate trigonometric coefficients to satisfy Only one of infinite choices, but yields TI model “My states, I make them up” Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Equating Coefficients l Example: l Arbitrary choice: a(t) = 1, b(t) = 0 Other choices don’t satisfy “constant-in-steadystate” desire, e. g. : l 28 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Extracting the Equations l Model is synthesized as: l vb is constant input, matrices are constants – 29 Will yield constant state variables in steady state Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

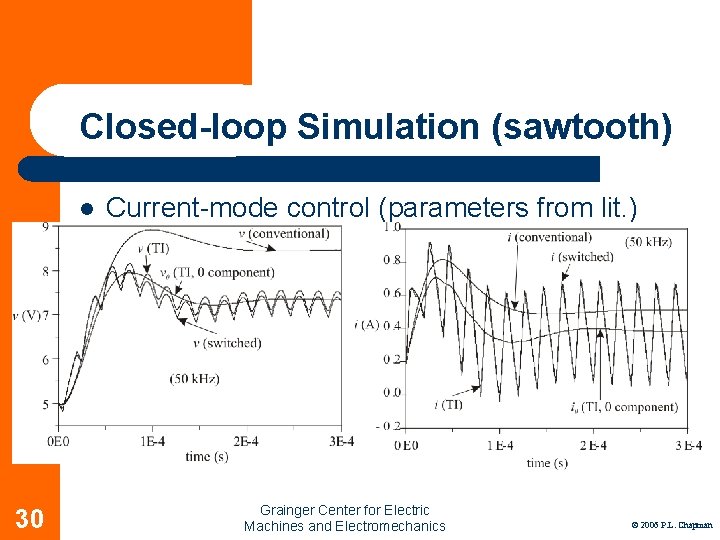
Closed-loop Simulation (sawtooth) l 30 Current-mode control (parameters from lit. ) Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

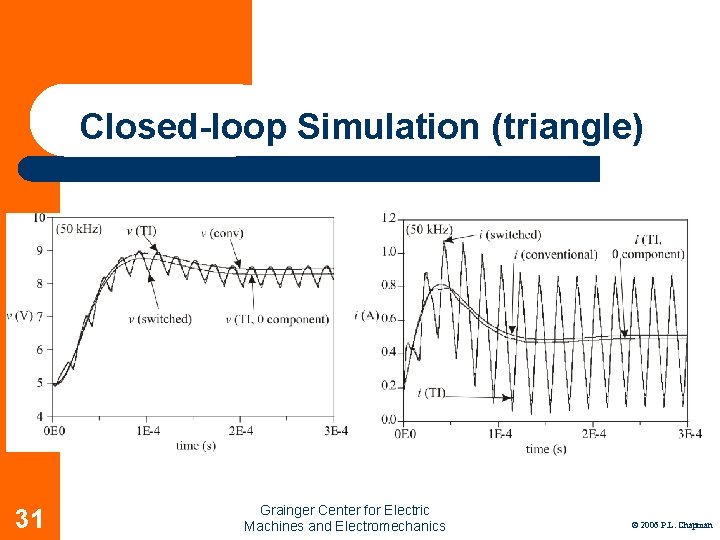
Closed-loop Simulation (triangle) 31 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Toward Error Bounds l l l Was tacitly assumed N was sufficient order Error will occur due to truncation of higher order terms Usually, error will be small given – – l 32 Low-pass filters Low levels of excitation at higher frequencies Can bound the steady-state error, if not transient Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Comparison with MFA l l l 33 Generates same state-space equations Slightly improved consideration of switching function here Avoided averaging integral Avoided “slow-varying” assumption Both neglect aliasing effects Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

More Comparison l l l 34 Both generally capture the average value more precisely Both rely on truncations of actual signals Allowed for sawtooth vs. triangular carrier Proposed method was not a unique formulation (infinite # of zero terms) Linearization (below) is analytical with proposed technique Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Small-Signal Analysis l Linearize the Qx terms (op = operating point) l Calculate the partials – 35 Messy derivation, but not bad end result (Sawtooh) Grainger Center for Electric Machines and Electromechanics (Triangle) © 2006 P. L. Chapman

Linearized Boost l 36 Includes 1 harmonic in duty cycle command, otherwise retains generality Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

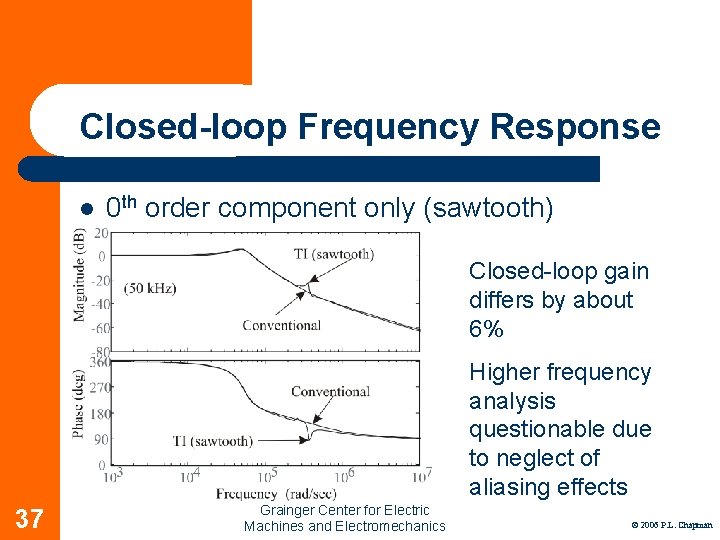
Closed-loop Frequency Response l 0 th order component only (sawtooth) Closed-loop gain differs by about 6% Higher frequency analysis questionable due to neglect of aliasing effects 37 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

“Disturbing” Issues l Switching and sampling not exactly the same – l But… – – l 38 Higher frequency disturbances are effectively aliased Signals aliased to low frequencies can pass through easily Absolute phase shift of input disturbance matters – l Can’t apply directly sampling theorems (in typical small-signal analysis, only relative phase matters) How can we account for this in a TI model? Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Sinusoidal Disturbances l l l 39 Can use ideas from sinusoidal PWM Once linearized and perturbed, we introduce unmodeled harmonics Choose important components from spectrum Let: Use Bessel-function approach to get specific components, e. g. : Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

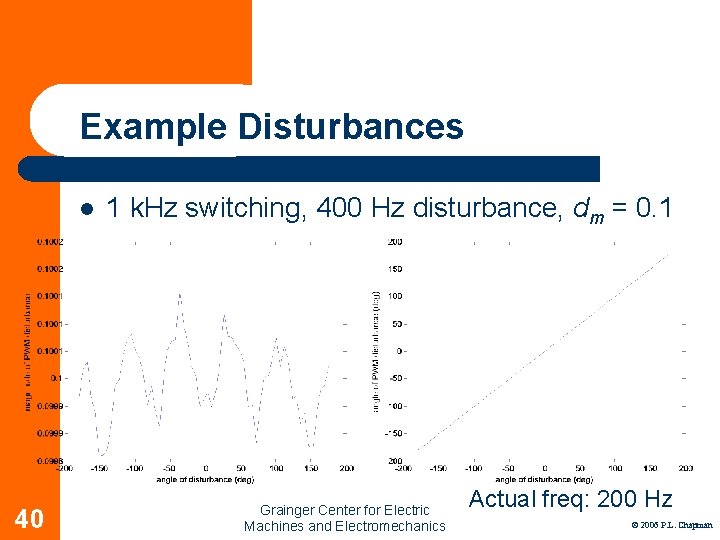
Example Disturbances l 40 1 k. Hz switching, 400 Hz disturbance, dm = 0. 1 Grainger Center for Electric Machines and Electromechanics Actual freq: 200 Hz © 2006 P. L. Chapman

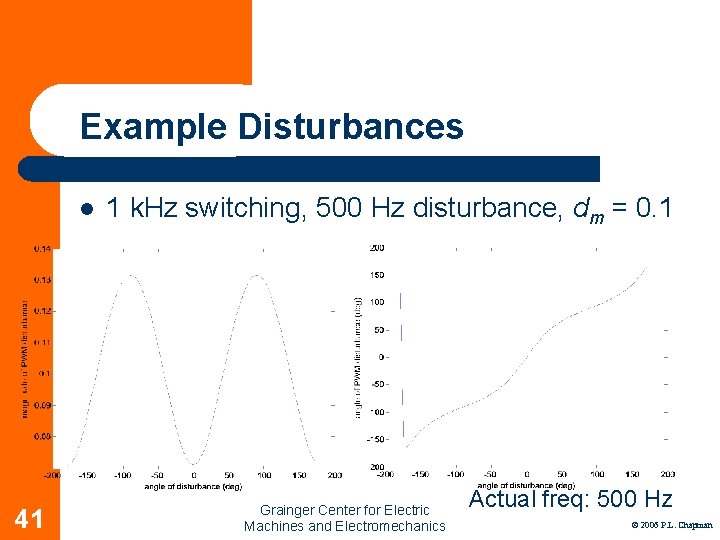
Example Disturbances l 41 1 k. Hz switching, 500 Hz disturbance, dm = 0. 1 Grainger Center for Electric Machines and Electromechanics Actual freq: 500 Hz © 2006 P. L. Chapman

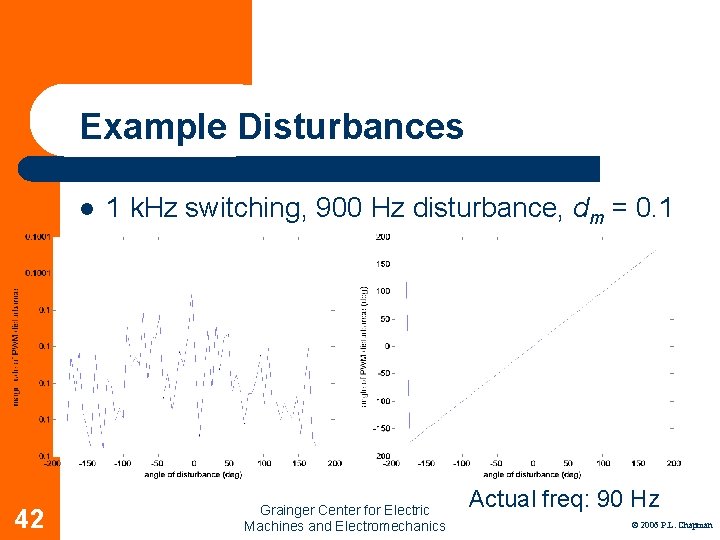
Example Disturbances l 42 1 k. Hz switching, 900 Hz disturbance, dm = 0. 1 Grainger Center for Electric Machines and Electromechanics Actual freq: 90 Hz © 2006 P. L. Chapman

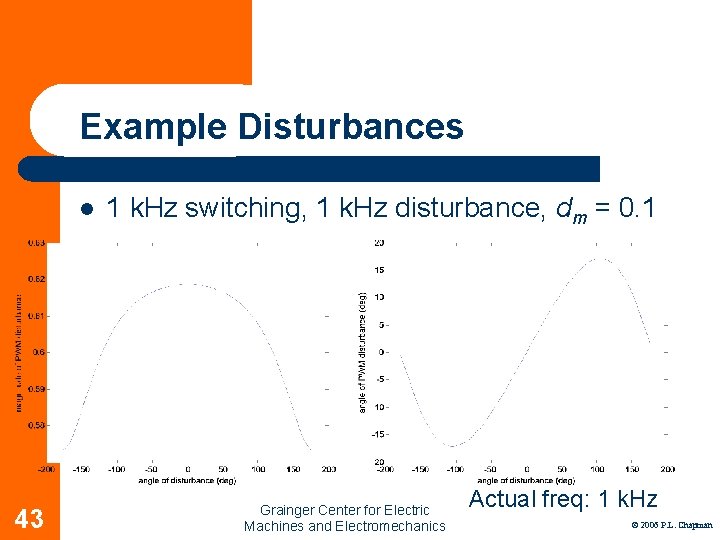
Example Disturbances l 43 1 k. Hz switching, 1 k. Hz disturbance, dm = 0. 1 Grainger Center for Electric Machines and Electromechanics Actual freq: 1 k. Hz © 2006 P. L. Chapman

Other Work in Progress l In most applications, the 2 nd order effects don’t matter that much – l l 44 Sometimes, we design so they won’t matter – but how can we be sure? How can we push the limit? Aliasing effects Digital sampling techniques Variable switching frequency Can we use MFA modeling techniques to investigate advanced controllers? Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Dominant Aliased Harmonic 45 l Looking between 0 and wsw only l Harmonics of wsw reduced by factor of l Model with an additional harmonic for fixed frequency disturbance analysis Grainger Center for Electric Machines and Electromechanics Relative sizes depend on fd © 2006 P. L. Chapman

Digital Sampling Effects l Voltage or current may be sampled – l Working with continuous time model – – – l 46 Analog to digital converter Sampling can be modeled as 0 th or 1 st order hold Quantization error These create additional harmonics in small-signal analysis Effects of (intentional? ) over- or undersampling Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Variable Switching Frequency l Useful during transients – – l 47 Speed up switching to increase dynamic performance Slow down during steady-state for lower switch losses Let wsw vary with time – must actually work in terms of qsw – the switching angle Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman

Conclusion l l Multi-frequency techniques can capture sometimesimportant 2 nd order effects Showed one technique that avoids formal averaging – – – l 48 Seems to have easy instantiation (suggests “tool”) Perhaps easier analysis Do other problems “crop up”? These methods have potential to tackle subtleties near and above fsw/2 Grainger Center for Electric Machines and Electromechanics © 2006 P. L. Chapman
 Dcdc detroit
Dcdc detroit Buck converter and boost converter
Buck converter and boost converter Helen c erickson
Helen c erickson Dimensional modeling vs relational modeling
Dimensional modeling vs relational modeling High boost filtering matlab
High boost filtering matlab 5x5 averaging filter matlab
5x5 averaging filter matlab What is the theme of without title
What is the theme of without title Without title for my father who lived without ceremony
Without title for my father who lived without ceremony Justify the title keeping quiet
Justify the title keeping quiet Four quadrant operation of dc dc converter
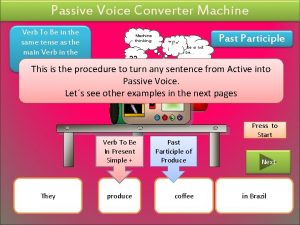
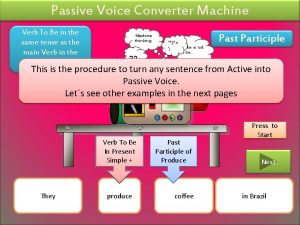
Four quadrant operation of dc dc converter Passive voice machine
Passive voice machine Contoh soal sinyal analog
Contoh soal sinyal analog Fungsi media converter
Fungsi media converter Automata
Automata Vortex flow torque converter
Vortex flow torque converter Pda to cfg conversion
Pda to cfg conversion Catalytic converter ingredients
Catalytic converter ingredients Microsoft virtual machine converter download
Microsoft virtual machine converter download Adc types
Adc types Language converter
Language converter Vrmat materials
Vrmat materials Converter inverter rectifier
Converter inverter rectifier Aziptv
Aziptv Www.freemake
Www.freemake Divisionsmetoden
Divisionsmetoden Halo vial adaptors
Halo vial adaptors Ytm5 converter
Ytm5 converter Y2cc converter
Y2cc converter Subset construction calculator
Subset construction calculator Charge pump converter
Charge pump converter Express the given hindu-arabic numeral in expanded form.
Express the given hindu-arabic numeral in expanded form. Switch mode converter
Switch mode converter Cyrillic to traditional mongolian converter
Cyrillic to traditional mongolian converter Active voice converter
Active voice converter Ladder diagram to mnemonic code converter
Ladder diagram to mnemonic code converter Whats fab
Whats fab State diagram to state table converter
State diagram to state table converter F to c formula
F to c formula Base-t to gigabit converter
Base-t to gigabit converter Opensim oar files
Opensim oar files Aub registrar
Aub registrar Eme converter
Eme converter Antaira media converter
Antaira media converter Igel desktop converter
Igel desktop converter Ayat aktif ke ayat pasif converter
Ayat aktif ke ayat pasif converter Buck converter failure modes
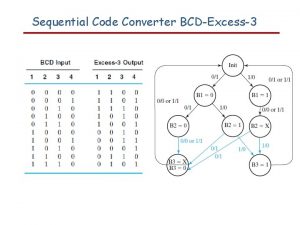
Buck converter failure modes Decimal to bcd encoder truth table
Decimal to bcd encoder truth table 3 phase full converter
3 phase full converter State various types of track electrification system
State various types of track electrification system