Linear Systems Timeinvariant systems ft Linear System gt

Linear Systems - Time-invariant systems f(t) Linear System g(t)

Linear System A linear system is a system that has the following two properties: Homogeneity: Scaling: The two properties together are referred to as superposition.

Time-invariant System A time-invariant system is a system that has the property that the shape of the response (output) of this system does not depend on the time at which the input was applied. If the input f is delayed by some interval T, the output g will be delayed by the same amount.

Harmonic Input Function Linear time-invariant systems have a very interesting (and useful) response when the input is a harmonic. If the input to a linear time-invariant system is a harmonic of a certain frequency , then the output is also a harmonic of the same frequency that has been scaled and delayed:

Transfer Function H( ) The response of a shift-invariant linear system to a harmonic input is simply that input multiplied by a frequency-dependent complex number (the transferfunction H( )). A harmonic input always produces a harmonic output at the same frequency in a shift-invariant linear system.

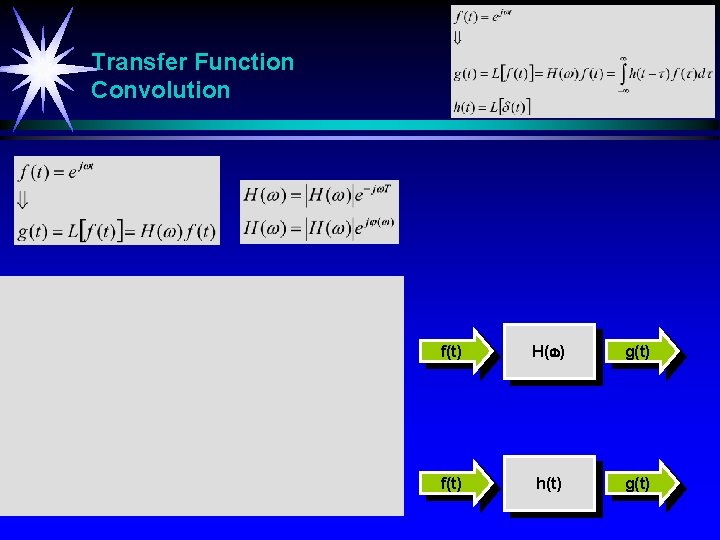
Transfer Function Convolution f(t) H( ) g(t) f(t) h(t) g(t)

Convolution f(t) h(t) g(t)

Impulse Response [1/4]

Impulse Response [2/4] f(t) h(t) g(t) F( ) H( ) G( )

Impulse Response [3/4] Convolution g(t) t

Impulse Response [4/4] Convolution = *

Convolution Rules

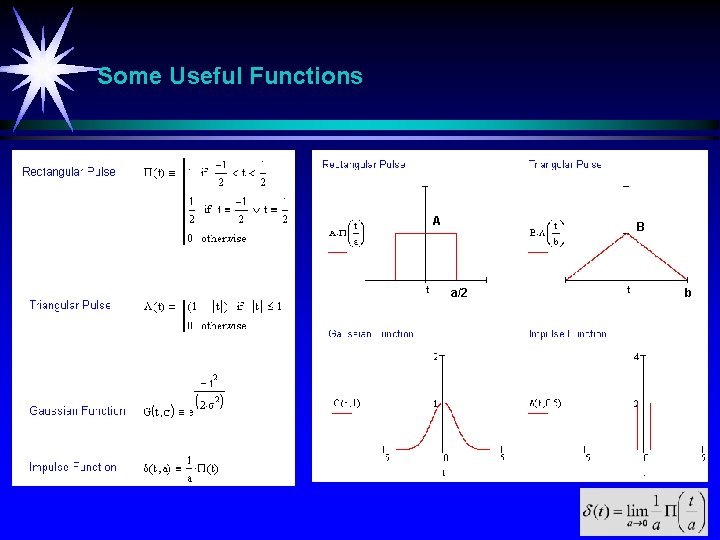
Some Useful Functions A B a/2 b

The Impulse Function [1/2] The impulse is the identity function under convolution

The Impulse Function [2/2]

Step Function [1/3] b b

Step Function [2/3] b b

Step Function [3/3] b

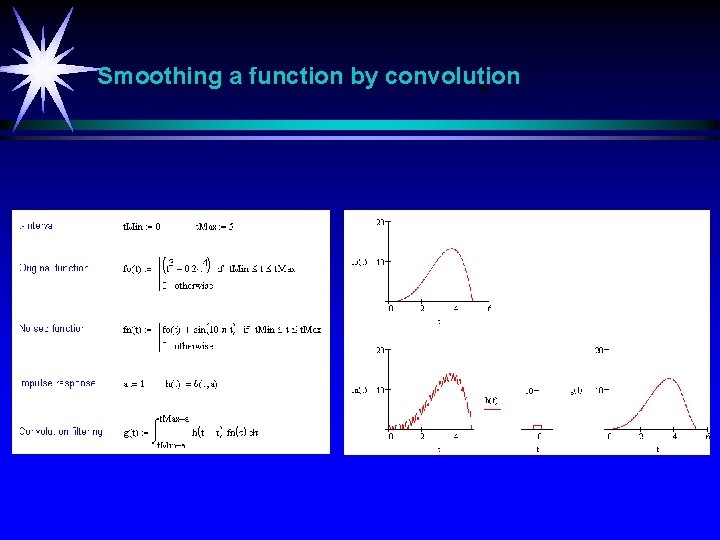
Smoothing a function by convolution b

Edge enhancement by convolution b

Discrete 1 -Dim Convolution [1/5] Matrix

Discrete 1 -Dim Convolution [2/5] Example

Discrete 1 -Dim Convolution [3/5] Discrete operation

Discrete 1 -Dim Convolution [4/5] Graph - Continuous / Discrete

Discrete 1 -Dim Convolution [5/5] Wrapping h index array

Two-Dimensional Convolution

Discrete Two-Dimensional Convolution [1/3]

Discrete Two-Dimensional Convolution [2/3]

Discrete Two-Dimensional Convolution [3/3] Kernel matrix Input image Array of products Output image Summer x. C Scaling factor Output pixel

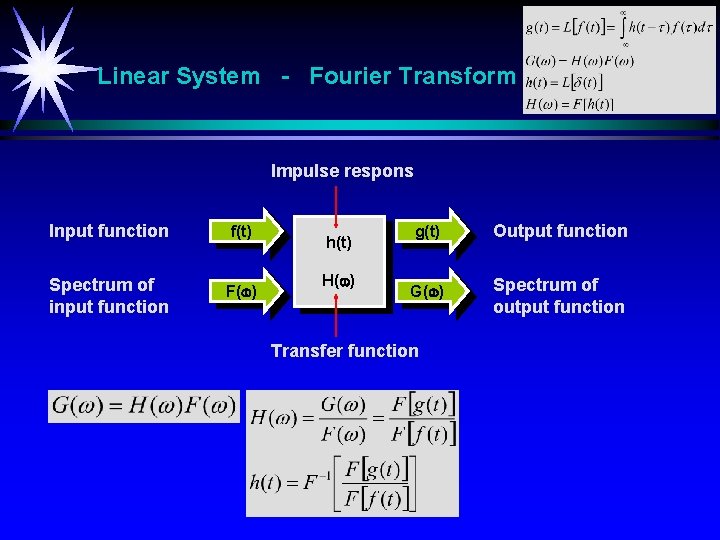
Linear System - Fourier Transform Impulse respons Input function f(t) Spectrum of input function F( ) h(t) H( ) g(t) Output function G( ) Spectrum of output function Transfer function

End