Channel Coding II Cyclic Codes and Convolutional Codes

Channel Coding (II) Cyclic Codes and Convolutional Codes 1

Topics today u u Cyclic codes – presenting codes: code polynomials – systematic and non-systematic codes – generating codes: generator polynomials – encoding/decoding circuits realized by shift registers Convolutional codes – presenting codes t convolutional encoder t code trees and state diagram t generator sequences ECED 4504 2 of 20

Defining cyclic codes: code polynomial 3 of 20 u An (n, k) linear code X is called a cyclic code when every cyclic shift of a code X, as for instance X’, is also a code, e. g. u Each cyclic code has the associated code vector with the polynomial u Note that the (n, k) code vector has the polynomial of degree of n-1 or less. Mapping between code vector and code polynomial is one-to-one, e. g. they specify the same code uniquely Manipulation of the associated polynomial is done in a Galois field (for instance GF(2)) having elements {0, 1}, where operations are performed mod-2 For each cyclic code, there exist only one generator polynomial whose degree equals the number of check bits in the encoded word u u ECED 4504

The common factor of cyclic codes 4 of 20 u GF(2) operations (XOR and AND): u Cyclic codes have a common factor pn+1. In order to see this we consider summing two (unity shifted) cyclic code vectors: Unshifted Right rotated Right shifted by multiplication u Question is how to make the cyclic code from the multiplied code? Adding the last two equations together reveals the common factor: ECED 4504

5 of 20 Factoring cyclic code generator polynomial u u u Any factor of pn+1 (Note: decompose it into factors) with the degree q=n -k generates an (n, k) cyclic code Example: Consider the polynomial p 7+1. This can be factored as For instance the factors 1+p+p 3 or 1+p 2+p 3, can be used to generate an unique cyclic code. For a message polynomial 1+p 2 (I. e. 110), the following encoded word is generated: and the respective code vector (of degree n-1, n=7, in this case) is ECED 4504

6 of 20 Obtaining a cyclic code from another cyclic code u Therefore unity cyclic shift is obtained by (1) multiplication by p where after (2) division by the common factor yields a cyclic code and by induction, any cyclic shift is obtained by u u u Example: right shift 101 (n=3) not a three-bit code, divide by the common factor Important point is that division by mod pn+1 and multiplication by the generator polynomial is enabled by tapped shift register. ECED 4504

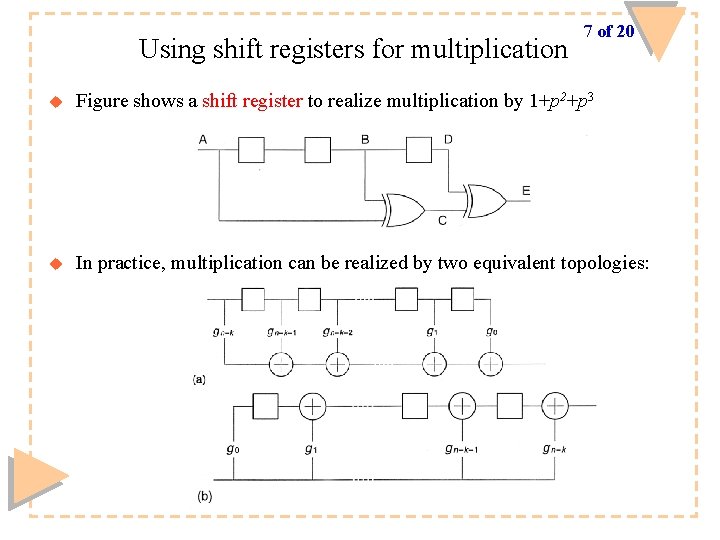
Using shift registers for multiplication 7 of 20 u Figure shows a shift register to realize multiplication by 1+p 2+p 3 u In practice, multiplication can be realized by two equivalent topologies: ECED 4504

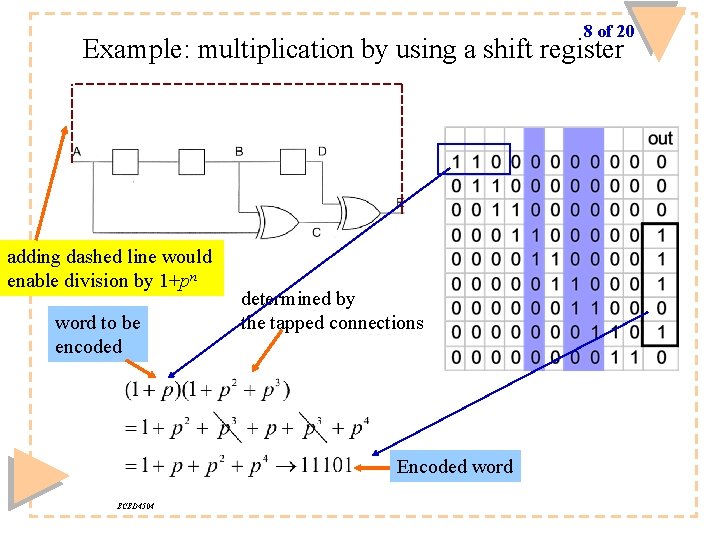
8 of 20 Example: multiplication by using a shift register adding dashed line would enable division by 1+pn word to be encoded determined by the tapped connections Encoded word ECED 4504

9 of 20 Examples of cyclic code generator polynomials u The generator polynomial for a (n, k) cyclic code is defined by and G(p) is a factor of pn+1. Any factor of pn+1 that has the degree q may serve as the generator polynomial. We noticed that a code is generated by the multiplication u where M(p) is a block of k message bits. Hence this gives a criterion to select the generator polynomial, e. g. it must be a factor of pn+1. Only few of the possible generating polynomials yield high quality codes (in terms of their minimum Hamming distance) Some cyclic codes: ECED 4504

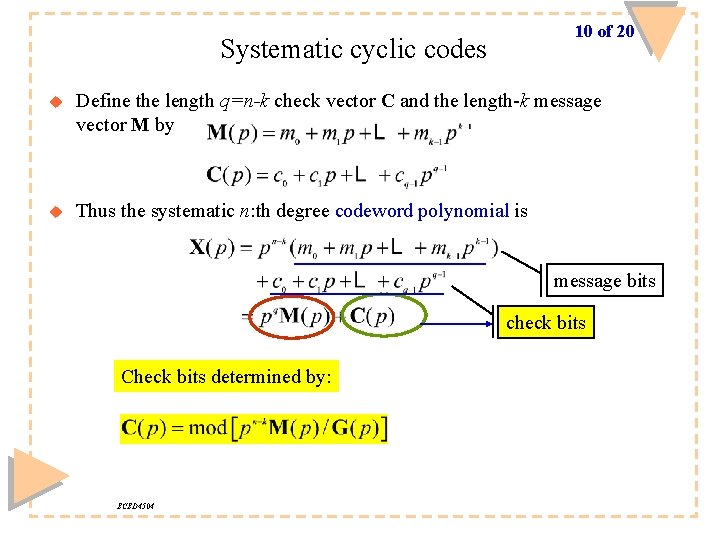
10 of 20 Systematic cyclic codes u Define the length q=n-k check vector C and the length-k message vector M by u Thus the systematic n: th degree codeword polynomial is message bits check bits Check bits determined by: ECED 4504

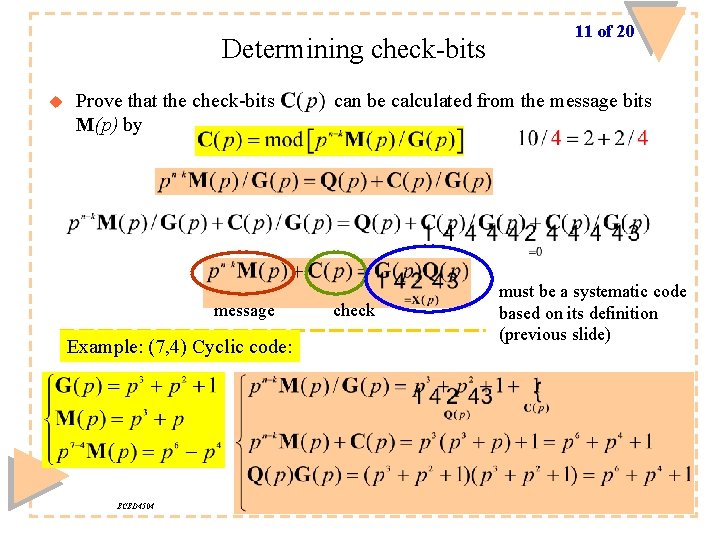
Determining check-bits u Prove that the check-bits M(p) by message Example: (7, 4) Cyclic code: ECED 4504 11 of 20 can be calculated from the message bits check must be a systematic code based on its definition (previous slide)

12 of 20 Example: Encoding of systematic cyclic codes ECED 4504

Decoding cyclic codes u u 13 of 20 Every valid, received code word R(p) must be a multiple of G(p), otherwise an error has occurred. (Assume that the probability for noise to convert code words to other code words is very small. ) Therefore dividing the R(p)/G(p) and considering the remainder as a syndrome can reveal if the error has happened and sometimes also to reveal in which bit (depending on code strength) u The error syndrome of n-k-1 degree is therefore u This can be expressed also in terms of error E(p) and the code word X(p) error syndrome S(p) is: ECED 4504

Decoding cyclic codes: example 14 of 20 Using denotation of this example: ECED 4504

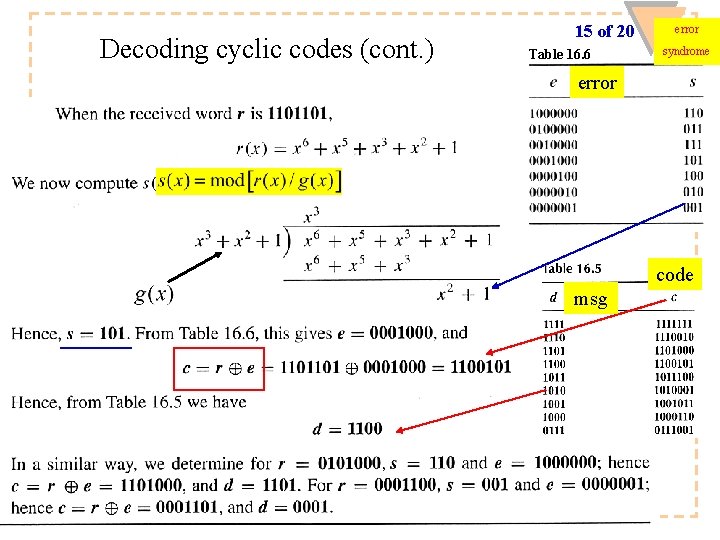
Decoding cyclic codes (cont. ) 15 of 20 Table 16. 6 error syndrome error code msg ECED 4504

Part II. Convolutional coding u u u 16 of 20 Block codes are memoryless Convolution codes have memory that utilizes previous bits to encode or decode following bits Convolutional codes are specified by n, k and constraint length that is the maximum number of information symbols upon which the symbol may depend Thus they are denoted by (n, k, L), where L is the code memory depth Convolutional codes are commonly used in applications that require relatively good performance with low implementation cost Convolutional codes are encoded by circuits based on shift registers and decoded by several methods as t Viterbi decoding that is a maximum likelihood method t Sequential decoding (performance depends on decoder complexity) t Feedback decoding (simplified hardware, lower performance) ECED 4504

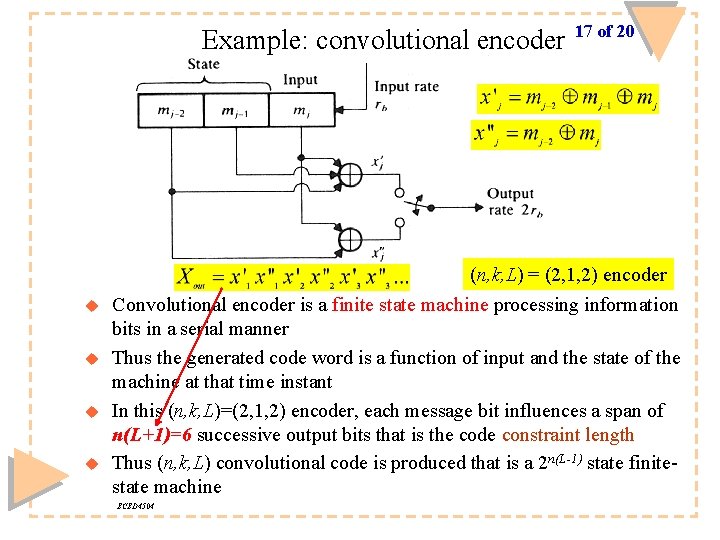
Example: convolutional encoder u u 17 of 20 (n, k, L) = (2, 1, 2) encoder Convolutional encoder is a finite state machine processing information bits in a serial manner Thus the generated code word is a function of input and the state of the machine at that time instant In this (n, k, L)=(2, 1, 2) encoder, each message bit influences a span of n(L+1)=6 successive output bits that is the code constraint length Thus (n, k, L) convolutional code is produced that is a 2 n(L-1) state finitestate machine ECED 4504

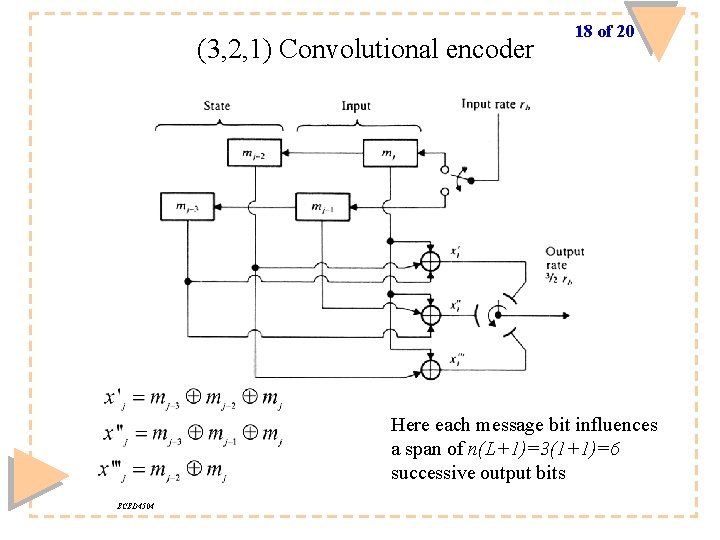
(3, 2, 1) Convolutional encoder 18 of 20 Here each message bit influences a span of n(L+1)=3(1+1)=6 successive output bits ECED 4504

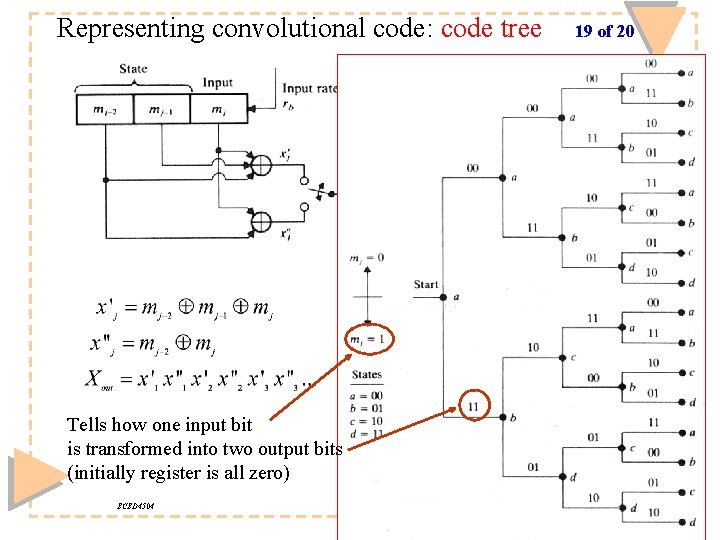
Representing convolutional code: code tree Tells how one input bit is transformed into two output bits (initially register is all zero) ECED 4504 19 of 20

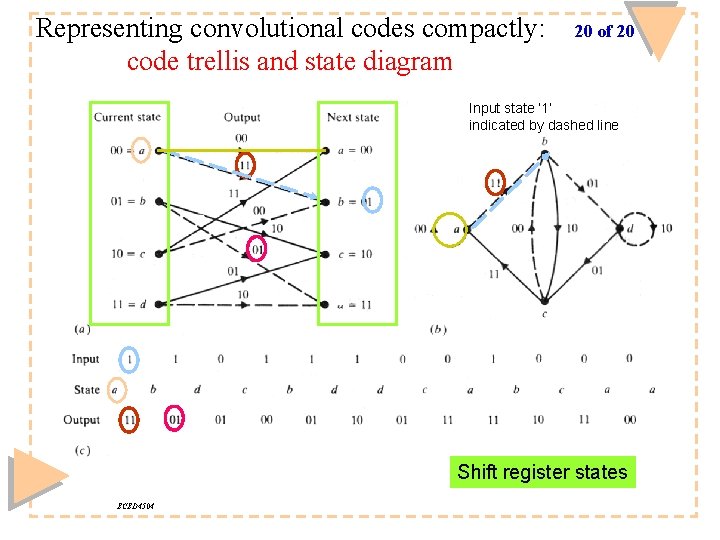
Representing convolutional codes compactly: code trellis and state diagram 20 of 20 Input state ‘ 1’ indicated by dashed line Shift register states ECED 4504