CENTRO DE ENSEANZA TCNICA INDUSTRIAL TEMA ECUACIONES DIFERENCIALES

CENTRO DE ENSEÑANZA TÉCNICA INDUSTRIAL TEMA: ECUACIONES DIFERENCIALES ALUMNO: Alejandro Montes Ramírez Reg. 9310440 PROFESOR: Mtro. César Octavio Martínez Padilla MATERIA: Ecuaciones Diferenciales a Miércoles 18 de Febrero de 2010

Ecuaciones Diferenciales Ø La ecuación diferencial es aquella ecuación que contiene las derivadas o diferenciales de una o más variables dependientes con respecto a una o más variables independientes.

El orden: Ecuación Diferencial Ø El orden de una ecuación diferencial (ordinaria o en derivadas parciales) es la derivada más alta contenida en ella. Ejemplo:

El grado: Ecuación Diferencial Ø El grado de una ecuación diferencial es la potencia a la que esta elevada la derivada más alta, siempre y cuando una ecuación diferencial esté dada forma polinomial.

Clasificación: Ecuaciones Diferenciales La ecuación diferencial contiene derivadas Ordinarias de una o más variables dependientes con respecto a una sola variable independiente. Tipo Parciales Orden La ecuación diferencial contiene derivadas parciales de una o más variables dependientes. Primer orden Segundo orden Tercer orden … Orden n F( x, y, y´)= 0 F ( x, y , y´´)=0 F( x, y, y´´, y´´´)=0 … F(x, y´´, …, y(n))=0

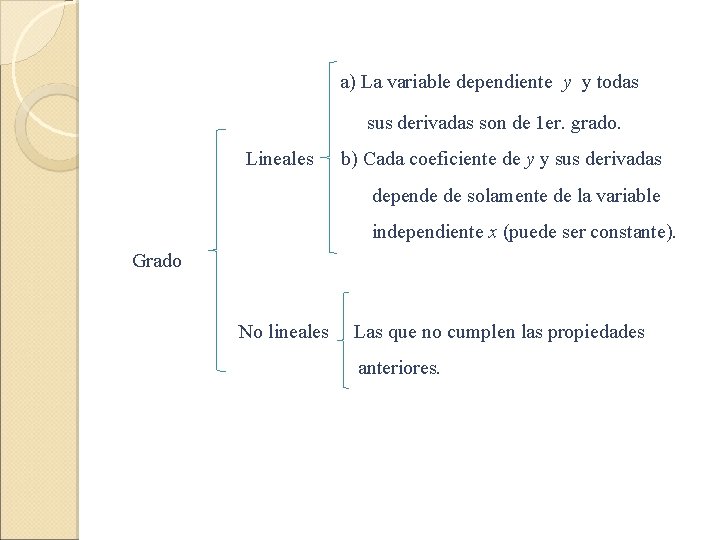
a) La variable dependiente y y todas sus derivadas son de 1 er. grado. Lineales b) Cada coeficiente de y y sus derivadas depende de solamente de la variable independiente x (puede ser constante). Grado No lineales Las que no cumplen las propiedades anteriores.

La solución: Ecuación Diferencial Ø La solución en una ecuación diferencial es una función que no tiene derivadas y que satisface a dicha función, esto quiere decir que al sustituir las funciones y sus derivadas en la ecuación diferencial resulta un identidad.

La solución: Ecuación Diferencial Otra manera de comprender sobre ¿ qué es la solución en una ecuación diferencial ? es la siguiente: Ø Cuando una función , definida en algún intervalo I, se sustituye en una ecuación diferencial y transforma esa ecuación en una identidad, se dice que es una solución en el intervalo.

Solución General: Ecuación Diferencial Ø La solución general en una ecuación diferencial es la función que contiene una o más constantes arbitrarias (obtenidas de las sucesivas integraciones).

Ejemplo: solución general La función x + y 2 = c es la solución de la ecuación diferencial: Por que derivándola implícitamente tenemos: 1 + 2 y , o expresado en otra forma: 2 yy´= -1 Sustituyendo (y) y (y´) obtenemos una identidad 2 donde

Solución Particular: Ecuación Diferencial Ø La solución particular de una ecuación diferencial es la función cuyas constantes arbitrarias toman un valor específico.

Ejemplo: solución parcial La función es la solución particular de la ecuación diferencial , por que derivando la solución y sustituyéndola en la ecuación dada, obtenemos: Por lo tanto 0=0

Interpretación Geométrica La interpretación de una ecuación diferencial es la descripción matemática de la misma para ello se mostrara según su orden, tipo y grado: Tipo Ordinaria Parcial Orden Grado Lineal 1 1 sí X 2 y´´+xy´+y = 0 Ordinaria 2 1 sí yy´´+x 3 y = x Ordinaria 2 1 No (Porque el coeficiente de y´´ no depende de x exclusivamente). y´+ y = x/y Ordinaria 1 1 No sen y´+ y=0 Ordinaria 1 ? No

Trayectorias Ortogonales Ø Las trayectorias ortogonales son las curvas que se intersectan formando un ángulo recto. Para obtener las trayectorias ortogonales de una ecuación diferencial, se toma: m 1= , como m 2= primera ecuación. de la trayectoria ortogonal a la

Existencia e unicidad Al resolver un problema de valor inicial surgen dos asuntos fundamentales: ¿Existe una solución al problema ? , si la hay ¿es única? Para un problema de valor inicial , en una ecuación, se pregunta lo siguiente: ¿La ecuación diferencial Existencia tiene soluciones ? ¿Alguna curvas solución pasa por el punto (x 0, y 0 )? ¿Cuándo podemos estar seguros que hay Unicidad precisamente una curva solución que pasa por el punto (x 0, y 0 )?

Ejemplo: Problema de valor inicial con varias soluciones Ambas funciones y = 0 y y = x 4/16 satisfacen la ecuación diferencial dx/dy = xy 3/2, y la condición inicial y = 0, de modo que el problema del valor inicial dx/dy = xy 1/2 , y(0)= 0 tiene dos soluciones cuando menos. Como vemos en la figura, la graficas ambas funciones pasan por el mismo punto, (0, 0)

Campo direccional Ø La terna (x, y, y´) determina la dirección de una recta que pasa por el punto (x, y). El conjunto de los segmentos de estas rectas es la representación geométrica del campo direccional.

Se puede resolver una ecuación diferencial trazando el campo direccional, en donde, para cada curva de la familia de solución, la tangente en cada uno de sus puntos tiene la misma dirección que el campo en ese punto.

Referencias • http: //dieumsnh. qfb. umich. mx/DIFERENCIAL/funciones. htm#VA RIABLES DEPENDIENTES.

Bibliografías � Ecuaciones Diferenciales, con aplicaciones al modelado Dennis G. Zill 6ª edición; 1997 Ed. Thomson � Ecuaciones Diferenciales con aplicaciones Dennis G. Zill 3ª edición; 1986 Ed. Grupo Editorial Iberoamérica

� Ecuaciones Diferenciales Isabel Carmona Jover 4ª edición; 1992 Ed. PEARSON , Addison Wesley Logman URL: http: //books. google. com. mx/books? id=f. KAZme. IP 0 b. AC&pg=PA 23 &dq=Que+es+el+grado+en+una+ecuacion+diferenciales&c

Glosario � Variables dependientes. - Son aquellas variables que como su nombre lo indica, dependen del valor que toma las otras variables Por ejemplo: f(x)= x, y o f(x) es la variable dependiente ya que esta sujeta a los valores que se le subministre a x. � Variable Independiente. - Es aquella variable que no depende de ninguna otra variable, en el ejemplo anterior la x es la variable independiente ya que la y es la que depende de los valores de x.